Здравствуйте, уважаемые читатели. В этой статье речь пойдет об одном подходе к автоматическому порождению программ по блочной модели задачи, к решению обратной задачи (восстановления модели исходной проблемы по уже порожденной программе), а также к решению проблемы верификации порожденных программ. Сама по себе тема очень серьезная, но статью я, по возможности, постараюсь сделать популярной (без тяжеловесного обзора аналогов, строго оформленной теоретической части и прочих сложностей), с примерами и описанием различных применений.
1. Автоматическое порождение программ
Для генерации любой программы требуется, прежде всего, знать, какую задачу мы решаем. Имея четкую формализованную постановку задачи, уже можно строить некие правила разворачивания этой постановки в план решения задачи и правила преобразования плана решения в конечный код на обобщенном или конкретном алгоритмическом языке. При этом обычно используется подход к построению конечной программы из готовых, созданных заранее, блоков – типовых алгоритмов, которые связываются неким вызывающим/обслуживающим кодом.
Пусть исходная постановка решаемой задачи представляется в виде блочной схемы (блоки могут быть элементарными или, в свою очередь являться подсхемами), например, сети объектов, каждый из которых относится к некоторому классу из иерархии классов-понятий предметной области. Такая постановка будет вполне наглядна и понятна как человеку, так и системе порождения программы. Такую постановку система должна преобразовать в план решения задачи по некоторым логическим правилам. Значит, правила такого преобразования было бы уместно писать на каком-нибудь языке логического программирования, я выбрал GNU Prolog. На практике, замечу, часто можно «пропустить» эту первую фазу (высокоуровневое описание задачи), сразу построив описание плана решения, также в виде блочной сетевой схемы.
Полученный план решения следует преобразовать в программу, как я уже писал, представляющую собой код, связывающий типовые алгоритмы решения «кирпичиков» задачи, реализованные, например, в виде библиотеки функций. Здесь возможны самые различные пути, опишу в нескольких словах использованный мной подход. Процесс порождения представляется в виде последовательности событий (например, генерация деклараций, генерация инициализационной части, этапы основной части, деинициализация), на каждое из которых сеть объектов должна покаскадно (имеются в виду каскады сети, такая схема исключает зацикливание модели при обработке события) реагировать генерацией соответствующих фрагментов кода. При этом объекты опираются на идентификатор события, значения своих параметров (задаются пользователем при построении блочной постановки задачи), а также на данные, которые они могут передавать друг другу по связям между ними. Поэтому каждый объект из плана решения имеет методы реакции на такие события, генерирующие код (а в общем случае – произвольный текст). Для решения такой задачи я выбрал язык PHP – он как раз прекрасно может генерировать произвольные текстовые фрагменты.
Настройка системы на предметную область выполняется путем разработки соответствующей иерархии порождающих классов.
Пример порождающего скрипта, генерирующего код для класса «Обработка вектора (минимум, максимум, среднее арифметическое)»:
<?
if ($Stage == stInit) {
$argumentID = $Arg["ID"][0];
$argumentSize = $Arg["Size"][0];
$resultID = GetNextMail("result" . $this->ID);
if ($this->Op == "Min") {
echo " " . $resultID . " = 1E300;n";
} else if ($this->Op == "Max") {
echo " " . $resultID . " = -1E300;n";
} elseif ($this->Op == "Avr") {
echo " " . $resultID . " = 0.0;n";
}
?>
for (i = 0; i < <? echo $argumentSize; ?>; i++)
<?
if ($this->Op == "Min") {
?>
if (<? echo $argumentID . "[i] < " . $resultID; ?>)
<? echo $resultID . " = " . $argumentID . "[i];n";
} else if ($this->Op == "Max") {
?>
if (<? echo $argumentID . "[i] > " . $resultID; ?>)
<? echo $resultID . " = " . $argumentID . "[i];n";
} elseif ($this->Op == "Avr") {
echo " " . $resultID . " += " . $argumentID . "[i];n";
}
if ($this->Op == "Avr") {
echo " " . $resultID . " /= " . $argumentSize . ";n";
}
}
?>
Это сравнительно несложная схема, которая работает. Система, реализующая такую схему порождения (PGEN++) позволяет, например, генерировать решающие программы в следующих областях:
а) моделирование процессов распространения загрязнений;
б) решение некоторых задач кинематики простых манипуляторов роботов;
в) простые учебные программы для работы с векторными данными (поиск минимума, максимума, среднего арифметического);
г) разработка тестов для системы психологического тестирования ПРОФТЕСТ.
Вот пример исходной постановки задачи (простая программа обработки векторных данных) в виде блочной схемы:
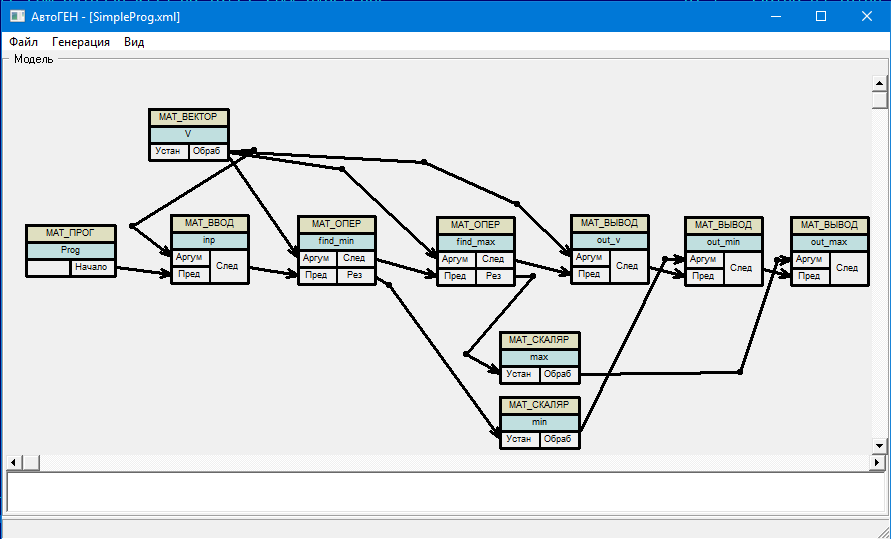
А это результат порождения программы:
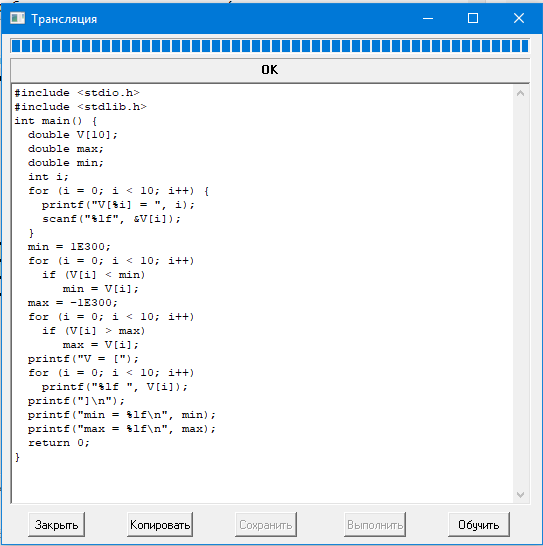
2. Обратная задача: реконструкция постановки задачи (исходной модели) по порожденной программе. Верификация порожденных программ
Прежде всего, для чего необходимо решение такой задачи. Ее прямое, и, думаю, самое очевидное применение – верификация автоматически порожденных программ. Если мы имели модель А, построили по ней программу П, из которой реконструировали модель Б, то программа, скорее всего, корректна при совпадении моделей А и Б.
Предлагается следующее простое решение. В автоматическом порождении программы фигурировали порождающие объекты, относящиеся к некоторой иерархии классов предметной области. Они имели только порождающие методы. Добавим к ним распознающие методы. Тогда исходная программа (или, в общем случае, любой текст) последовательно сканируется распознающими методами каждого класса, который, при успешном распознавании, генерирует объект/объекты этого класса. Получаем упорядоченный (в порядке «чтения» текста) набор параметризованных элементов модели. Остается определить связи между ними на основании порядка следования объектов и соотношения между их параметрами. Для этого можно применить специальные решающие правила.
Распознающий метод, в моей реализации, состоит из распознающей части (это группа модифицированных регулярных выражений) и решающей части (написанной на GNU Prolog). Регулярные выражения модифицированы таким образом, чтобы осуществлять некоторую предобработку (проверка по словарю, нечеткая проверка по похожести по Левенштейну, проверки на сбалансированность выражений по скобкам) еще на стадии разбора, для этого в них добавлена возможность включать разнообразные цепочки (проверяющие, добавляющие, удаляющие, обучающие нейронную сеть) «быстрых» предикатов.
Эта схема также работает. В качестве прямого применения она использовалась для реконструкции простых учебных программ для работы с векторными данными (поиск минимума, максимума, среднего арифметического), в таком случае она вполне успешно продемонстрировала возможную верификацию порожденных программ путем сравнения исходной и реконструированной моделей. Но есть и иные применения, о них дальше.
3. Естественно-языковой интерфейс для системы порождения программ
При решении обратной задачи (описана выше) нет каких-либо ограничений на вид исходных материалов для восстановления модели решаемой задачи. Это вполне может быть текст на естественном языке. Просто надо написать соответствующие распознающие методы. Поэтому, неожиданным применением обратной задачи может быть реализация естественно-языкового интерфейса к системе порождения:
а) пишется постановка задачи на упрощенном естественном языке;
б) решается обратная задача – из естественно-языковой постановки извлекается формальная постановка (сеть объектов-элементов предметной области);
в) система запускается на порождение программы по полученной формальной постановке.
И эта схема тоже работает. Пример разработан для того же случая простых учебных программ для работы с векторными данными.
Вот пример распознающего метода (класса «Ввод с клавиатуры вектора или скаляра»), который разбит на две версии (распознавание текта программы (режим Programmatical) или распознавание фрагмента постановки задачи на русском языке (режим Russian)). Сверху идет распознающая часть, далее решающие предикаты на GNU Prolog.
@versions(Programmatical)
@global_unique(PROCESS,infinity):-
(s*fors*(is*=s*0;s*is*<s*(d+)->{N};s*i++)s*{\ns*printf("(w+)->{VECTOR}
[%i]s*=s*",s*i);\ns*scanf("%lf",s*&(w+)==>{VECTOR}[i]);\ns*}\n)|
(s*printf("(w+)->{SCALAR}s*=s*");\ns*scanf("%lf",s*&(w+)==>{SCALAR});\n).
@versions(Russian)
@nearest(db_vvedem,2,"db_vvedem.csv").
@fast(db_var,"db_var.csv").
@global_unique(PROCESS,infinity):-
(()->{VAR}([А-Яа-я]+)?=>{db_vvedem($)}s+((сs+клавиатурыs+)?)->{KEYB}
([А-Яа-я]+)?=>{db_var($,$VAR)}s+(w+)->{ID}((s+сs+клавиатуры)?)!=>{KEYB}s*.).
@versions(Russian)
handle:-xpath('PROCESS','//ID/text()',[VText]),
xpath('PROCESS','//VAR/text()',['0']),
simple_vector(_,VText,_),
global_id(GID),assertz(simple_act(GID,in,VText,'')),!.
handle:-xpath('PROCESS','//ID/text()',[SText]),
xpath('PROCESS','//VAR/text()',['1']),
global_id(GID),assertz(simple_act(GID,in,SText,'')),!.
@versions(Programmatical)
handle:-xpath('PROCESS','//VECTOR/text()',[VText]),
xpath('PROCESS','//N/text()',[NText]),
simple_vector(_,VText,NText),
global_id(GID),assertz(simple_act(GID,in,VText,'')),!.
handle:-xpath('PROCESS','//SCALAR/text()',[SText]),
simple_scalar(_,SText),
global_id(GID),assertz(simple_act(GID,in,SText,'')),!.
@versions(Programmatical,Russian)
@goal:-
handle,!.
@done:-
clear_db.
Пример постановки задачи на русском языке:
Составить программу. Ввести скаляр max. Ввести скаляр min.
Введем вектор V из 10 элементов. Зададим вектор V с клавиатуры. Найдем минимум вектора V и поместим результат в скаляр min.
Найдем также максимум вектора V и поместим результат в скаляр max. Вывести скаляр min на экран. Вывести скаляр max на экран.
Вывести вектор V на экран.
А среднее арифметическое считать не будем.
И модель задачи, полученная системой из приведенного выше естественно-языкового описания:
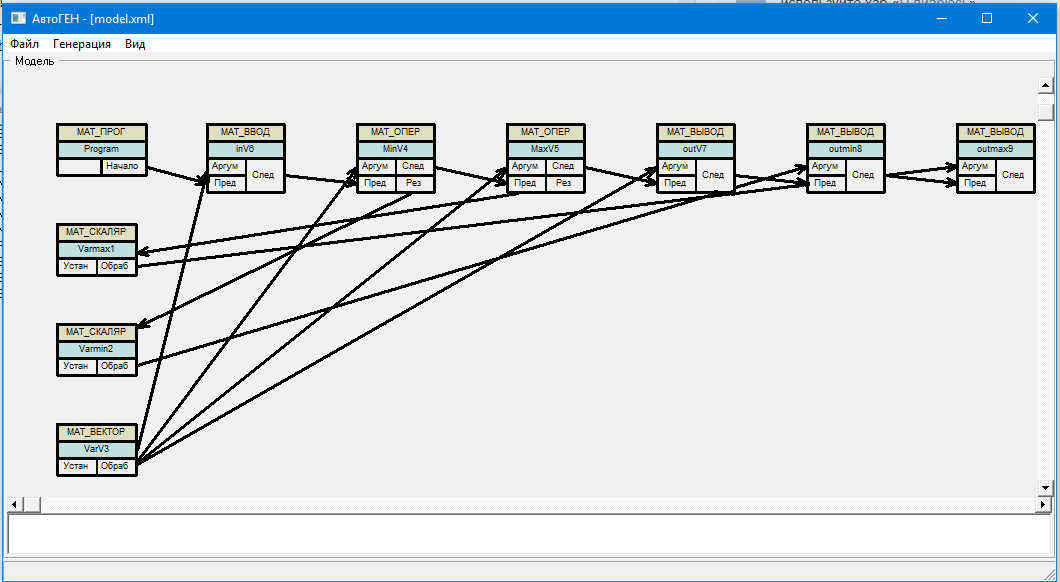
4. Иные применения обратной задачи
Ничто не мешает при решении обратной задачи рассмотреть случай не просто распознавания некоторой программы, а ее распознавание «с улучшением» или иной (произвольного характера) переработкой. В частности, удалось разработать «автоматический параллелизатор» распознаваемой программы, написанной на языке C. Она проводит статический и, отчасти, динамический анализ распознаваемого кода и вставляет в него директивы распараллеливания из расширения Cilk/Cilk++. Такая задача улучшения реализуется распознающими методами (на GNU Prolog).
Пример вычислительной C-программы, обработанной параллелизатором (он вставил директивы cilk_spawn и cilk_sync):
#include <stdio.h>
#include <math.h>
#include <omp.h>
#define PI 3.14159265358
#define NX 100
#define NY 100
#define MaxT 0.001
#define h 0.01
#define tau 0.00001
#define cilk_spawn _Cilk_spawn
#define cilk_sync _Cilk_sync
void F( double x, double y, double t, double * val ){
double r = sqrt(x*x + y*y);
double result = 0.0;
int i;
for ( i = 0; i < 300; i++ )
result += exp(-r*t)*sin(0.1*i*r + 0.5*PI);
*val = result;
}
int main( ){
double f[NY][NX] = {0.0};
double v[NY][NX] = {0.0};
double v1[NY][NX] = {0.0};
double t;
int x, y;
double start = omp_get_wtime();
for ( t = 0.0; t < MaxT; t += tau )
{
for ( y = 1; y < NY-1; y++ )
for ( x = 1; x < NX-1; x++ )
cilk_spawn F(x*h, y*h, t, &f[y][x]);
for ( y = 1; y < NY-1; y++ )
for ( x = 1; x < NX-1; x++ )
{
cilk_sync;
v1[y][x] = v[y][x] + tau*((v[y-1][x]+v[y+1][x]+v[y][x-1]+v[y][x+1]-4.0*v[y][x])/h/h - f[y][x]);
}
for ( y = 1; y < NY-1; y++ )
for ( x = 1; x < NX-1; x++ )
v[y][x] = v1[y][x];
}
for ( y = 0; y < NY; y++ )
{
for ( x = 0; x < NX; x++ )
printf("%lf ", v[y][x]);
printf("n");
}
printf("Total time = %lfn", omp_get_wtime() - start);
return 0;
}
5. Немного фантастики. Верификация и идентификация произвольных программ с закрытым исходным кодом
Здесь речь уже идет о произвольных программах, написанных программистом и/или системой порождении программ, для которых просто нет исходного кода. Пусть требуется проверить корректность функционирования такой программы, или хотя бы даже понять, чем она занимается. В таком случае может быть использован тот или иной вариант так называемого «метаслоя» — гипотетического компонента операционной системы, который отслеживает всю последовательность работы программы (вызов функций, модификация данных в памяти и т.п.) и строит по ней приблизительную модель ее логики в виде эквивалентной по функционированию программы на каком-либо языке программирования. После чего остается решить для такой программы обратную задачу – восстановить возможную исходную модель (или модели), которые позволили бы хотя бы оценить правильность или понять предназначение программы. Прототип такого «метаслоя» когда-то разрабатывался автором для случая C/C++-программ, удалось не так уж много, но кое-что работало. Возможно, когда-нибудь кто-нибудь захочет такую работу выполнить в полноценном объеме.
6. Заключение
Надеюсь, что сумел продемонстрировать, что и автоматическое порождение программ и решение обратной задачи – не чисто академические проблемы, а нечто полезное и имеющее прямые практические следствия. При этом изложенные здесь решения не претендуют на полноту и очевидность, но они реализованы и претендуют на определенную новизну.
Автор: Vladimir Pekunov





