Приветствую уважаемое сообщество.
Последнее время я уделял некоторое внимание теме синтаксического анализа (с целью в том числе улучшить собственные знания и навыки), и у меня создалось впечатление, что почти все курсы по компиляторам начинают с математических формализмов, и требуют сравнительно высокого уровня подготовки от изучающего. Либо там используется в большом количестве формальная математическая запись, как в классической Dragon Book, в которой, например, написано:
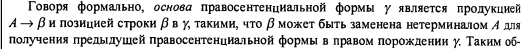
Это может с непривычки напугать. Нет, с какого-то момента формальная запись становится удобной и даже необходимой, но для “человека с улицы”, который хотел бы, чтобы ему “на пальцах” объяснили, “в чем тут дело”, это может быть сложно. А вопрос “что такое LL и LR — анализ, и в чем между ними разница” программисты задают довольно часто (потому что не все программисты имеют формальное образование в области Computer Science, как и я, и не все из них проходили там курс по компиляторам).
Мне более близок подход, когда сначала мы берем задачу, пытаемся ее решить, и в процессе решения сначала вырабатываем интуитивное понимание принципа, а потом уже для этого понимания создаем математические формализмы. Поэтому я на очень простом примере в этой статье хочу показать, какая идея лежит в основе восходящего синтаксического анализа (он же bottom-up parsing, он же LR). Будем вычислять арифметическое выражение, в котором для еще большего упрощения будем поддерживать только операторы сложения, умножения и скобки (чтобы не усложнять пример отрицательными числами и поддержкой унарного минуса).
Перед тем, как перейти непосредственно к задаче, напишу некоторые соображения вообще на тему синтаксического разбора.
Синтаксический разбор — это одно из фундаментальных понятий в компьютерной науке (в той ее части, что о формальных языках, фактически языках программирования), поэтому к необходимости разобраться в этой теме приходит рано или поздно почти любой программист. Особенно когда ему начинает хотеться написать какой-нибудь мини-интерпретатор какого-нибудь мини-языка, который ему рано или поздно захочется реализовать. Причем иногда программист может даже не осознавать, что он конструирует интерпретатор, а думать, что вот он придумал «удобный формат» для описания каких-то «правил», или «действий», или «конфигурации», и теперь ему надо «этот формат читать». По моему мнению, это закономерный процесс, который приводит к концепции языково-ориентированного программирования, когда язык общего назначения используется для создания интерпретатора DSL (Domain Specific Language), и дальше этот DSL все шире используется в проекте, потому что так как-то само собой получается, что эту предметную область описывать удобнее именно с помощью DSL.
Поэтому синтаксический разбор и важен, что интерпретатор без него не построишь. А задача вычисления арифметических выражений — наверное, одна из самых простых задач, которая для своего решения уже требует синтаксического разбора. Поэтому обычно ознакомление с этой сложной темой начинают чаще всего с нее.
Как можно вычислить арифметическое выражение? Можно преобразовать его в Reverse Polish Notation и вычислить на стэке, можно написать анализатор, который вычислит его методом рекурсивного спуска, можно использовать shunting yard algorithm, можно использовать генератор синтаксических анализаторов (ANTLR или bison), который по составленной грамматике сделает синтаксический анализатор, и вычислить выражение в нем.
Но использование инструментов, таких как ANTLR или bison оставляет ощущение, что ты запустил какую-то магию, тебе сгенерировали синтаксический анализатор по грамматике, которую ты составил, и дальше ты его используешь и не понимаешь, как он работает. Как будто тебе его дали свыше какие-то высшие силы, превосходящие способности твоего понимания. Кроме того, при использовании этих инструментов мы всегда начинаем плясать от грамматики языка, который хотим разбирать, а сама по себе задача составить грамматику не так уж проста. Надо понимать, что это такое, как она работает, как устранять левую рекурсию (и что это такое вообще), почему некоторые грамматики для LR могут не работать для LL и как их переписывать, если надо, чтобы работали, и все такое. Сразу это может быть сложно, особенно если такое понятие, как «грамматика» (и предшествующие ей понятия «продукция», «терминальный символ», «нетерминальный символ», «правосентенциальная форма» и много других страшных слов) еще не входит в понятийный аппарат («активный словарный запас») программиста, который пытается написать ну, допустим, тот же вычислитель арифметических выражений. Поэтому для понимания концепции восходящего синтаксического анализа можно попробовать решить какую-нибудь простую задачу, но самостоятельно.
Переходим к задаче: будем вычислять арифметическое выражение, используя некую разновидность восходящего (bottom-up) анализа (если точнее, то этот метод называется “синтаксический анализ приоритета операторов”). Алгоритм неоптимальный, но зато простой для понимания. Он напоминает тоже неоптимальный, но понятный и поэтому всем известный алгоритм пузырьковой сортировки.
Чтобы не углубляться в частности, поступим как ленивые ленивцы, и будем поддерживать только операторы * (умножение), + (сложение) и скобки. Перед тем, как пойдем дальше, задержимся на скобках.
В самом деле, представим себе, что нам не надо поддерживать скобки. Тогда алгоритм вычисления выражения получается очень простым и понятным:
- Просканировать строку слева направа, и выполнить все операторы умножения (допустим, на входе была строка 1 + 5 * 7 + 3, на выходе получилось 1 + 35 + 3)
- Просканировать то, что получилось на шаге 1, и выполнить все операторы сложения (было на входе 1 + 35 + 3, получилось на выходе 39).
- Отдать то, что получилось на шаге 2, в качестве результата.
Не нужен никакой синтаксический анализ! Входная структура является плоской, и для работы с ней синтаксический анализ не требуется. Необходимость в нем появляется, когда появляется необходимость поддерживать скобки (и другие аналоги — операторные скобки begin..end, вложенные блоки, и т. п.). Входная структура перестает быть плоской и становится древовидной (то есть самоподобной, рекурсивной), и с этого момента для работы с ней тоже нужно применять рекурсивные методы и методы синтаксического анализа. То есть, например, 5 * (2 + 3) — это выражение, но и (2 + 3) — это тоже выражение. И то и другое можно дать на вход синтаксическому анализатору выражений. Но про синтаксический анализ методом рекурсивного спуска сейчас речь не идет, так что пойдем дальше.
Чтобы много не заниматься сейчас лексическим анализом, договоримся, что лексическим анализатором для нас выступит функция String.split (для тех, кто забыл или пока «не в теме» — лексический анализатор — эта такая штука, которой мы на вход даем строку, а она нам нарезает ее на массив подстрок(токенов). В нашем случае это будет, например ' ( 2 + 3 ) ' -> ['(', '2', '+', '3', ')'])
Неформальное описание нашего алгоритма будет таким:
- Просканировать строку, раскрыть все скобки, какие можем.
- Просканировать строку, выполнить все операторы умножения, какие можем.
- Просканировать строку, выполнить все операторы сложения, какие можем.
Как мы поймем, что можем выполнить оператор умножения или сложения? По признаку, что и слева, и справа от оператора — число. Как мы поймем, что можно раскрыть скобки? Когда внутри скобок — только выражение, в котором нет никаких других скобок.
Собственно, дальнейшее, мне кажется, будет понятным из текста программы и вывода результата ее работы. (Учтите, в программе могут быть ошибки, она писалась чисто для демонстрационных целей).
package demoexprevaluator;
import java.io.PrintStream;
import java.util.ArrayList;
public class DemoExprEvaluator {
// какая же многословная эта ваша Java...
public class CalcResult {
public boolean operationOccured;
public String resultString;
public CalcResult(boolean op, String r){
this.operationOccured = op;
this.resultString = r;
}
}
// вспомогательная функция для облегчения работы лексическому анализатору
public String spreadSpaceBetweenTokens(String s){
StringBuilder r = new StringBuilder();
for (int i = 0; i<s.length(); i++){
Character c = s.charAt(i);
if (c.equals('(') || c.equals(')') || c.equals('+') || c.equals('*')) {
r.append(" ").append(c).append(" ");
}
else if (Character.isDigit(c)) {
r.append(c);
}
}
return r.toString().trim();
}
// лексическим анализатором у нас будет работать функция String.split
public String[] getLexems(String expr) {
expr = spreadSpaceBetweenTokens(expr);
String[] lexems = expr.split("\s+"); // плюс нужен, чтобы не было пустых лексем (токенов)
return lexems;
}
// выполняет применение оператора к выражению.
public String applyOperator(String exprWithoutParens, String operator) {
ArrayList<String> stack = new ArrayList<>();
String[] lexems = getLexems(exprWithoutParens);
for(int i = 0; i < lexems.length; i++) {
stack.add(lexems[i]);
if (stack.size() >= 3) {
String left = stack.get(stack.size()-3);
String middle = stack.get(stack.size()-2);
String right = stack.get(stack.size()-1);
if (Character.isDigit(left.charAt(0)) && middle.equals(operator) && Character.isDigit(right.charAt(0))){
Integer operand1 = Integer.valueOf(left);
Integer operand2 = Integer.valueOf(right);
Integer res = 0;
if (operator.equals("*")) {
res = operand1 * operand2;
}
if (operator.equals("+")) {
res = operand1 + operand2;
}
stack.remove(stack.size()-1); // like "pop"
stack.remove(stack.size()-1);
stack.remove(stack.size()-1);
stack.add(res.toString());
}
}
}
return String.join("", stack);
}
// вычисляет выражение, в котором не должно быть скобок
public String evalExprWithoutParens(String exprWithoutParens) {
// здесь определяем приоритеты операторов: сначала выполняем вызов для умножения, потом для сложения
String result = applyOperator(exprWithoutParens, "*");
result = applyOperator(result, "+");
return result;
}
// мы ничего не имеем права складывать, пока мы все не перемножили
// мы ничего не имеем права перемножать, пока мы не раскрыли все скобки
// скобки мы имеем право раскрыть только тогда, когда внутри скобок все сложено и перемножено
// но мы имеем право складывать и перемножать все, что внутри парных вложенных скобок, причем других парных вложенных скобок между ними нет
// ...(2+2)... -> ...4...
public CalcResult openSingleParen(String expr) {
CalcResult r = new CalcResult(false, expr);
String[] lexems = getLexems(expr);
ArrayList<String> stack = new ArrayList<>();
int lpindex = 0;
for(int i = 0; i < lexems.length; i++){
String lexem = lexems[i];
stack.add(lexem);
if (lexem.equals("(")) {
lpindex = i;
}
if (lexem.equals(")") && !r.operationOccured) {
stack.remove(stack.size()-1);
int numOfItemsToPop = i - lpindex - 1;
StringBuilder ewp = new StringBuilder(); // ewp <=> expression without parethesis
for (int j = 0; j < numOfItemsToPop; j++) {
ewp.insert(0, stack.get(stack.size()-1));
stack.remove(stack.size()-1);
}
System.out.println("about to eval ewp:" + ewp);
String ewpEvalResult = evalExprWithoutParens(ewp.toString());
stack.remove(stack.size()-1); // removing opening paren from stack
stack.add(ewpEvalResult);
r.operationOccured = true;
}
}
r.resultString = String.join("", stack);
return r;
}
public void Calculate(String expr) {
System.out.println("They want us to calculate:" + expr);
CalcResult r = new CalcResult(false, expr);
// раскрываем все скобки
while (true) {
System.out.println(r.resultString);
r = openSingleParen(r.resultString);
if (!r.operationOccured) {
break;
}
}
// сейчас в r.resultString скобок уже нет, можно довычислить выражение
r.resultString = evalExprWithoutParens(r.resultString);
System.out.println("The result is: " + r.resultString);
}
public static void main(String[] args) {
DemoExprEvaluator e = new DemoExprEvaluator();
String expr = "2+300*(4+2)*((8+5))";
e.Calculate(expr);
}
}
Вывод работы:
They want us to calculate:2+300*(4+2)*((8+5))
2+300*(4+2)*((8+5))
about to eval ewp:4+2
2+300*6*((8+5))
about to eval ewp:8+5
2+300*6*(13)
about to eval ewp:13
2+300*6*13
The result is: 23402
Вот. Настоящие LR-анализаторы гораздо сложнее, их обычно вручную не пишут, а используют для их автоматической генерации формальные грамматики и специальные инструменты, такие как bison (раньше он был yacc), которые на основе грамматик генерируют программный код, реализующий LR-анализатор. Но терминология shift-reduce, которую используют при описании таких анализаторов, надеюсь, стала понятнее. Когда мы сканировали нашу строку, и добавляли токены в стэк, мы делали shift. Когда мы применяли оператор умножения, сложения или раскрывали скобки — мы делали reduce.
Напоследок упомяну про LL-анализ (рекурсивный спуск). Исторически он появился раньше, чем LR, более или менее общим мнением является то, что LL-анализаторы сравнительно просто писать вручную, а LR обычно создаются с помощью генераторов. Но для автоматической генерации LL-анализаторов тоже существуют инструменты, один из самых известных — ANTLR. Наверное, умение написать LL-анализатор вручную делает работу с такими инструментами легче. Какой подход применять (LL или LR) — вопрос холиворный, поэтому ответ, наверное, “кому какой нравится, и у кого какие навыки лучше отработаны”.
Тем не менее, LL-анализ заслуживает отдельной статьи, которую я, возможно, напишу в будущем (будем разбирать что-то вроде JSON).
Автор: klvov


