Когда у тебя в запасе много популярных инструментов вроде JAVA, Python, Ruby, PHP, C#, C++ и других, чувствуешь себя почти всемогущим. Стандартный подход в разработке рулит. Но только до тех пор, пока не столкнешься с определенным типом задач.
Подумайте, как правильно написать программу, которая оптимально…
• решит головоломку типа судоку или задачу о восьми ферзях;
• распределит задачи между определенным набором ресурсов;
• рассчитает расписание занятий;
• определит эффективный маршрут движения транспорта;
• составит график дежурств и т.п.
Если программирование в ограничениях и решение сложных комбинаторных задач планирования не самая сильная ваша сторона, то эта статья как раз для вас.
Возьмем в качестве примера одну из задач календарного планирования – расчет графика дежурств. Какие сложности могут возникнуть у программиста при выборе алгоритма расчета графика? На первый взгляд, все очень просто. Можно использовать простой алгоритм. Случайным образом или лучше последовательно равномерно распределять дежурства между сотрудниками.
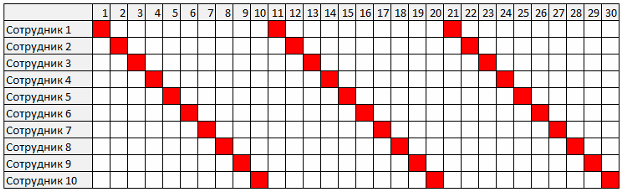
Это идеальный вариант. Однако в реальной жизни все гораздо сложнее. Обычно существует множество дополнительных условий, которые обязательно надо учитывать. Сотрудники уходят в отпуска или переносят дни и, как следствие, появляются сдвиги. Становится еще сложнее, если требуется учитывать пожелания сотрудников, дежурства разбиты на несколько смен или выбор человека зависит от уровня его квалификации и так далее. В какой-то момент простой алгоритм перестает работать. Можно попытаться пойти другим путем – искать оптимальное решение среди множества всех возможных комбинаций. Однако здесь возникает другая проблема.
Сама по себе проблема оптимального распределения дежурных с соблюдением всех ограничений не нова. Существует уже более 40 лет и известна, как Nurse scheduling problem (NSP).
В чем сложность? Задачи планирования относятся к разделу математики комбинаторика. Обычно у такого рода задач бывает не одно, а множество вариантов решений и иногда очень большое. Простой пример. Сколькими способами можно составить график дежурств на период в 30 дней, когда каждый день дежурит один сотрудник из 10? Получается 10 в 30 степени (нониллион) способов. Если условия аналогичные, но сутки разбиты на три смены (один сотрудник в смене), получаем 
в 30 степени вариантов. Отыскать оптимальный вариант среди такого большого количества комбинаций методом полного перебора не под силу даже саму мощному компьютеру.
Еще одна сложность: большинство задач планирования входят в класс сложных комбинаторных задач NP-hard. Плохая новость в том, что для NP-hard задач нет эффективного универсального алгоритма (полиномиального), позволяющего найти доказуемо оптимальное решение за разумное время.
Хотя теоретически такой алгоритм может существовать, но вопрос до сих пор остается открытым (см. Равенство классов P и NP). Цена вопроса – 1 000 000$ (см. Задачи тысячелетия).
Хорошая новость: несмотря на отсутствие волшебной таблетки или серебряной пули, выход все-таки есть. Существуют различные подходы, позволяющие найти близкое к оптимальному решение для такого вида задач за приемлемое время.
Комбинаторная задача как задача удовлетворения ограничений
Для удобства решения комбинаторной задачи, ее можно представить в виде задачи удовлетворения ограничений (Constraint satisfaction problem, CSP). CSP состоит из простой описательной схемы: список переменных (variables), для каждой из которых задан набор возможных значений (domains), и список ограничений (constraints), которым переменные должны удовлетворять. Решением в CSP является нахождение всех возможных значений, которые переменные могут принимать в соответствии с условиями заданных ограничений.
Простой пример CSP
- Переменные:
- Ограничения:
- Решение:
CSP не определяет конкретные алгоритмы решения. Существует много разных подходов. Некоторые из них можно представить так…
- Техники целочисленного программирования (Integer programming):
- Алгоритм Гомори (Cutting-plane method);
- Метод ветвей и границ (Branch and bound).
- Алгоритмы локального поиска (Local search):
- Алгоритм имитации отжига (Simulated annealing);
- Алгоритм пороговой допустимости (Threshold accepting);
- Поиск с запретами (Tabu search);
- Генетические алгоритмы (Genetic algorithms);
- Алгоритм Min-conflicts.
- Нейронные сети (Neural networks).
Часто используются специализированные методы решения CSP, например, дерево поиска совместно с алгоритмом поиска с возвратом.
CSP и программирование в ограничениях
В области планирования и календарного планирования подходит и часто используется технология программирования в ограничениях (Constraint programming, CP). Компьютерная реализация алгоритмов для эффективного решения больших комбинаторных задач. В отличие от привычной формы императивного программирования, в CP используется декларативное. Это упрощает работу: достаточно только описать проблему, все вычисления и поиск значений выполняет решатель (Solver), содержащий эффективные алгоритмы вычислений.
Программирование в ограничениях неразрывно связано с задачей удовлетворения ограничений. Поэтому описанную ранее в качестве примера CSP, очень легко представить в виде программы.
Например, на языке MiniZinc она будет выглядеть следующим образом:
% VARIABLES
var {1,2,3}: X;
var {1,2}: Y;
var {1,2,3}: Z;
% CONSTRAINTS
constraint X != Y;
constraint X = Z;
constraint Y < Z;
% SOLVER
solve satisfy;
% OUTPUT
output ["X=", show(X), " Y=", show(Y), " Z=", show(Z)];
После завершения работы программа выведет все допустимые значения переменных в соответствии с заданными ограничениями:
X=2 Y=1 Z=2
----------
X=3 Y=1 Z=3
----------
X=3 Y=2 Z=3
----------
Для программирования в ограничениях используются как отдельные среды программирования с поддержкой CP, так и подключаемые библиотеки в обычных языках программирования.
Подключаемые библиотеки:
- Google Optimization Tools (OR-Tools) (C++, Python, .Net, Java)
- Gecode (C++, Gecode_Interfaces)
- Chuffed (C++)
- COIN-OR CBC (C++)
- OptaPlanner (Java)
- JaCoP (Java)
- Choco (Java)
- CHIP V5 (C++)
- Microsoft Solver Foundation (.Net)
Отдельные среды программирования:
- MiniZinc
- IBM ILOG CPLEX
- AIMMS
- ECLiPSe Constraint Programming System
- Babelsberg
- The Mozart Programming System
- HAL
- Screamer для Common Lisp
- Curry
- Constraint Handling Rules (CHR)
- The Elf Meta-Language
График дежурств в формате CSP
Возьмем в качестве примера проблему расчета графика дежурств. Представим его в виде модели CSP. Условия задачи будут заведомо упрощенными и нести исключительно ознакомительный характер.
Легенда
- Необходимо рассчитать график дежурств для 10 человек на период в 30 дней.
- Каждый день в дежурстве участвуют два сотрудника, один заступает основным дежурным и второй резервным.
- У каждого сотрудника за весь временной период общее количество основных дежурств должно быть больше или ровно трем.
- На следующий день после основного дежурства сотрудник заступает резервным дежурным, далее следует один или более дней отдыха.
1. Исходные данные
- n – количество дней в расчетном периоде (n=30)
- m – количество дежурных (m=10)
- d – индекс дня (d = 1,…,n)
- e – индекс сотрудника (e = 1,…,m)
2. Переменные (VARIABLES)
Определим набор переменных Х в виде двухмерной матрицы. Порядок переменных в каждой строке соответствуют дням дежурств для определенного сотрудника.
Домен допустимых значений для переменных:
3. Ограничения (CONSTRAINTS)
В каждый день только один сотрудник может быть основным дежурным.
![$sum_{e=1}^m[x_{e,d}=1]=1 (d=1, 2,...,n)$](https://www.pvsm.ru/images/2017/11/22/zadachi-planirovaniya-i-programmirovanie-v-ogranicheniyah-15.svg "Задачи планирования и программирование в ограничениях - 15")
Квадратные скобки – обозначение в нотации Айверсона
![$[P]=begin{cases}1,&если P true\0,&если P falseend{cases}$](https://www.pvsm.ru/images/2017/11/22/zadachi-planirovaniya-i-programmirovanie-v-ogranicheniyah-16.svg "Задачи планирования и программирование в ограничениях - 16")
В каждый день только один сотрудник может быть резервным дежурным.
![$sum_{e=1}^m[x_{e,d}=2]=1 (d=1, 2,...,n)$](https://www.pvsm.ru/images/2017/11/22/zadachi-planirovaniya-i-programmirovanie-v-ogranicheniyah-17.svg "Задачи планирования и программирование в ограничениях - 17")
Количество основных дежурств по каждому сотруднику за весь временной период должно быть больше или равно трем.
![$sum_{d=1}^n[x_{e,d}=1] geq 3 (e=1, 2,...,m)$](https://www.pvsm.ru/images/2017/11/22/zadachi-planirovaniya-i-programmirovanie-v-ogranicheniyah-18.svg "Задачи планирования и программирование в ограничениях - 18")
Определим детерминированный конечный автомат. Опишем порядок распределения дежурств. После основного дежурства сотрудник заступает резервным дежурным, далее следует один или более дней отдыха. Переходы между состояниями обозначены: main=1 – основное дежурство, reserve=2 – резервное дежурство, off=3 – день отдыха.
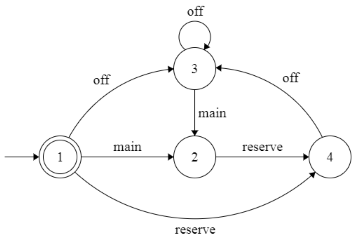
Описание состояний автомата в виде таблицы переходов:
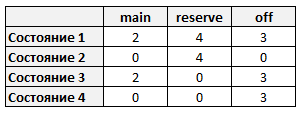
Сформулировать задачу можно было разными способами. Например, представить набор значений X в виде трёхмерной матрицы с доменом значений один и ноль (третье измерение для трех типов дежурств). Или для каждого типа дежурств определить отдельную переменную.
Практическая реализация графика дежурств на MiniZinc
А теперь быть может самое интересное. Напишем реальную программу рассчитывающую график дежурств согласно заданным условиям CSP. В качестве среды программирования в ограничениях будем использовать MiniZinc.
MiniZinc – это высокоуровневый язык моделирования ограничений с открытым кодом. В отличии от других CP сред программирования он полностью независим от решателей (solver-independent). На MiniZinc легко строить модели разной сложности и экспериментировать с ними на решателях сторонних производителей. В арсенале языка содержится библиотека с большим количеством глобальных ограничений (Global constraints MiniZinc), а также есть возможность создавать пользовательские ограничения (предикаты). Это сильно упрощает моделирование прикладных проблем.
Независимость от решателей достигается за счет трансляции программ MiniZinc в более низкоуровневый код FlatZinc. FlatZinc через интерфейсы поддерживается большим количеством решателей.
MiniZinc доступен для использования на большинстве платформ (Windows, Mac OS, Linux), а так же имеет отдельное IDE.
Для более подробного знакомства с языком MiniZinc настоятельно рекомендуется прочитать руководство MiniZinc Tutorial, где в очень понятной форме описаны все особенности языка и есть много примеров.
Перепишем модель графика дежурств CSP в код программы MiniZinc, выполним программу и решим задачу.
include "regular.mzn";
%--------------------------------------------------
% 1. INITIAL DATA. Исходные данные
%--------------------------------------------------
int: n = 30;
int: m = 10;
set of int: D = 1..n;
set of int: E = 1..m;
% функция переходов конечного автомата
array[1..4, 1..3] of int: dfa_states = [|2, 4, 3
|0, 4, 0
|2, 0, 3
|0, 0, 3
|];
%-------------------------------------------------
% 2. VARIABLES. Переменные
%-------------------------------------------------
array[E, D] of var 1..3: X;
%-------------------------------------------------
% 3. CONSTRAINTS. Правила
%-------------------------------------------------
% 3.1 В каждый день только один из сотрудников может быть основным дежурным
% 3.2 В каждый день только один из сотрудников может быть резервным дежурным
% Объединяем оба условия в одно через конъюнкцию /
constraint
forall(d in D)(
sum(e in E)( bool2int( X[e, d] = 1 )) = 1
/
sum(e in E)( bool2int( X[e, d] = 2 )) = 1
);
% 3.3 Количество основных дежурств по каждому из сотрудников, за весь временной период должно быть больше или равно трем
constraint
forall(e in E)(
sum(d in D)( bool2int( X[e, d] = 1 )) >= 3
/
regular( [X[e, d] | d in D], 4, 3, dfa_states, 1, 1..4 )
% regular - глобальное ограничение, определяет значения набора переменных согласно правилам из функции переходов (dfa_states)
);
%-------------------------------------------------
% SOLVE
%-------------------------------------------------
solve satisfy;
%-------------------------------------------------
% OUTPUT
%-------------------------------------------------
array[1..3] of string: rest_view = ["M", "R", "-"];
output
[
rest_view[fix(X[e, d])] ++ " " ++
if d = n then "n" else "" endif
| e in E, d in D
];
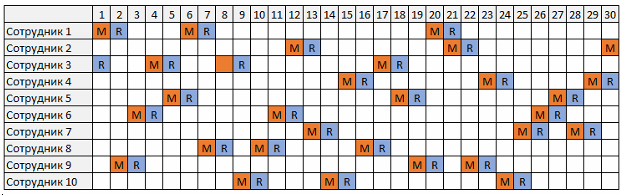
После завершения выполнения программы получаем один из возможных вариантов графика дежурств. Последовательность распределения дежурств для каждого сотрудника (горизонтальные строки), где M (Main) – основное дежурство, R (Reserve) – резервное дежурство, "-" – сотрудник не дежурит.
M R - - - - - - M R - - - - M R - - - - - - - - - - - - - -
R - - - - M R - - - M R - - - - - - - - - M R - - - - - - -
- - - - - - - M R - - - - - - M R - - - - - - - M R - - - -
- - - - - - M R - - - - - - - - M R - - - - - - - - M R - -
- M R - - - - - - - - - - - - - - - - - M R - M R - - - - -
- - M R - - - - - M R - - - - - - - - - - - M R - - - - - -
- - - - - - - - - - - - M R - - - - - M R - - - - - - M R -
- - - - M R - - - - - M R - - - - - - - - - - - - - - - M R
- - - - - - - - - - - - - M R - - - M R - - - - - - - - - M
- - - M R - - - - - - - - - - - - M R - - - - - - M R - - -
Или если это представить в более понятном виде, то так:
Если заранее известны даты отпусков, когда сотрудник не должен дежурить или, наоборот, нужно зафиксировать дежурство определенного сотрудника на конкретную дату, то это можно сделать через дополнительные ограничения. Например, чтобы пятый сотрудник был основным дежурным первого числа, а второй сотрудник не дежурил шестого, задаем ограничение:
constraint X[5,1]=1 / X[2,6]=3;
Чуть более сложный вариант программы (Hakan Kjellerstrand), можно найти здесь
Заключение
У счастливого обладателя молотка может возникнуть иллюзия, что инструмент подходит для решения любых проблем. Но молоток не универсален, а в некоторых случаях его преимущества совсем неочевидны. И таких случаев бывает много. Так и в программировании, некоторые задачи решаются неправильно или неоптимально, если не используются специализированные подходы. Программирование в ограничениях — это мощный инструмент, другая парадигма, помогающая эффективно решать большое количество практических комбинаторных задач.
Много полезной информации о программировании в ограничениях можно найти в блоге Hakan Kjellerstrand, также большое количество примеров задач MiniZinc здесь или здесь.
Ссылки по теме:
Nurse scheduling problem
Удовлетворение ограничений
Программирование в ограничениях
MiniZinc Home Page
MiniZinc Tutorial
The MiniZinc Challenge
Автор: trusted
![Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс]](https://www.pvsm.ru/wp-content/plugins/contextual-related-posts/timthumb/timthumb.php?src=http%3A%2F%2Fwww.pvsm.ru%2Fimages%2F2024%2F05%2F10%2Fkak-obhitrit-mozg-i-zastavit-ego-polyubit-slojnye-zadachi-dofaminovyi-detoks-9.jpg&w=100&h=100&zc=1&q=75 "Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс]")
