После публикации на Хабре своей первой статьи, об одном из способов организации иерархии в реляционной БД, у меня осталось чувство не доведенного до конца дела.
Судя по комментариям, кто-то принимал предложенный метод за другой, спрашивали чем не устраивает “django-mttp”, рассказывали о поддержке деревьев в PostgreSQL…
Спасибо всем отписавшимся, но из-за сумбурного изложения в самой статье, думаю, что я не сумел донести до читателя то, что хотел. А “если я чего решил, то выпью обязательно”(с)
Поэтому, я решился на еще одну попытку изложения интересующего меня подхода. А именно — хранение иерархии в числовом коде, вычисляемом на основании данных о размерности дерева. То есть, заранее определены максимальные количество Уровней и количество Детей у каждого Родителя (возможные диапазоны достаточно велики, поэтому, заранее пугаться этого не стоит). При таких вводных, код, каждого иерархического элемента, будет являться и путем до него, и включать диапазон всех Детей. А это сулит скорость, и много еще чего…
Далее — с картинками и таблицами, без привязки к какой-либо БД (ибо это не важно). В конце статьи есть ссылки на реализацию на Django.
Методы хранения иерархии
Описание и сравнение наиболее распространенных методов реализации иерархии в реляционных БД можно найти в прекрасных статьях Михаила Стадника aka Mikhus:
Иерархические структуры данных и Doctrine
Иерархические структуры данных и производительность
Кто еще не читал но интересуется данным вопросом — рекомендую. Доступное изложение и богатый примерами текст, избавляют меня от необходимости все пересказывать (тем более так хорошо у меня точно не получится).
Для вступления, по моему, уже достаточно, поэтому перехожу к сути вопроса.
С чего это мне взбрело в голову
Итак, мне таки понадобилось однажды хранить иерархию. Изначально был выбран незамысловатый и простой в реализации метод хранения ключа в строке. То есть дерево должно было выглядеть примерно так:
Рис.1
Предполагалось иметь две таблицы — Группы и Элементы (сейчас не важно чего). Иерархическая таблица с Группами относительно(!) небольшая и изменяется редко. Таблица с Элементами, напротив, допускает большое их количество и активно правится, точнее больше растет. И еще более активно из нее происходят выборки в границах Групп, определенных в первой таблице.
Я умышленно не пускаюсь в пространные описания выбранного метода, в его обоснованность, предназначение БД и всего приложения. Это не принципиально для моего сегодняшнего повествования. (к тому же предложенный мной далее метод можно будет использовать и при работе с одной таблицей)
Таблица — Группы
1. ID — Char
2. PARENT — Char — Ссылка на ID
…
Таблица — Элементы
1. ID — Integer
2. GROUP — Char — Ссылка на ID в таблице Групп
….
Такой подход работает. Плохо или хорошо, другой вопрос. Надо помнить, что всегда есть плюсы и минусы. Для предполагаемого приложения мне такой метод подходил.
После некоторых размышлений, мне пришло в голову, что символьные строки вполне можно заменить на ключи целого типа (Да! это будет работать быстрее, и занимать меньше места, и проще реализовать, и просто — выглядит красиво...). Главное обеспечить не пересекающиеся вложенные диапазоны. Почему нет?
Далее речь пойдет только об одной таблице — иерархической.
Первоначально я попробовал изобразить все дерево кодами в двоичной системе. Получилось. Поняв суть, нарисовал небольшое дерево с 3-я уровнями и 3-я возможными Детьми у каждого Элемента. Выглядело это так (система, конечно, десятичная):

Рис.2
Смотрится конечно не привычно.
Цифры сверху — показывают размер таблицы, для удобства, слева — Уровни.
Каждое число это ID Элемента (жирным).
Дети у Элемента — внизу и справа до следующего Элемента на том же уровне. Например, Дети у Элемента=16 это диапазон 16<ID<(31+1)
На Рис.2 уже полностью заполненное дерево, чтобы было наглядно.
Вот кусочек дерева в более традиционном представлении:
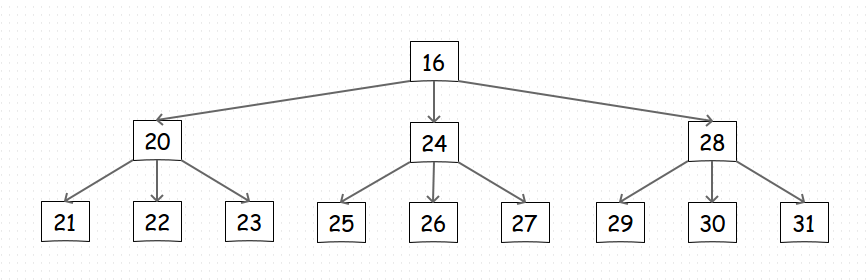
Рис.3
На этом рисунке, сходу уловить периодику труднее, да и дерево всё не видно. Поэтому подпишу слева еще один столбик, который нам поможет далее, и покажу дерево в более “нативном” виде:

Рис.4
Очень легко заметить зависимости.
В любом Элементе — есть степень 4-ки, то есть (ДопустимоеКоличествоДетей + 1).
На самом верхнем,1-м уровне, это 4^2, на 2-м — 4^1, на 3-м — 4^0.
Другими словами, (ДопустимоеКоличествоДетей + 1) надо возводить в степень равную (ДопустимоеКоличествоУровнейВДереве - ТекущийУровеньНовогоЭлемента). Нужная степень и указана в “красном” столбике. Но не просто надо возводить, а еще и прибавлять к Родителю столько раз, каким по счету ребенком он является.
Для разнообразия, покажу таблицу для дерева, с количеством Уровней=4 и Детей=2:

Рис.5
По аналогии вы сами уже сможете понять, какое здесь основание и степень.
Если есть затруднения, маленький пример по Рис.5…
Допустим, имеем Элемент с кодом 27. Детей еще нет.
Чтобы получить 1-го Ребенка, надо:
27 + ((2+1)^2) * 1 = 36
Чтобы получить 2-го Ребенка:
27 + ((2+1)^2) * 2 = 45
и т.д. и т.п…
Вот, собственно, и всё. Остальное дело техники.
Вычисление id нового Ребенка
Если дерево заполнено, то оно самодостаточно. То есть, зная его размерность, мы можем по ID вычислить УровеньЭлемента и его место в Родительском узле.
Но нам только предстоит создавать дерево, причем без лишних запросов к БД.
Поэтому я ввел поле COUNT_CHILDS, чтобы можно было взять следующий свободный ID для Ребенка.
Так же для вычисления ID, понадобится знать текущий УровеньРодителя. Дополнительных запросов это не потребует (добавляя нового Ребенка мы “находимся” на Родителе), поэтому я добавил поле LEVEL. Уровень можно и вычислить, кому интересно, без труда это смогут сделать. Но я просто ввел дополнительное поле.
В итоге имеем такую иерархическую структуру таблицы:
ID — Integer
PARENT — Integer — ссылка на ID
LEVEL — Integer
COUNT_CHILDS — Integer
Пусть размерность Дерева будем обозначать:
LV — Количество Уровней
CH — Количество Детей у одного Родителя
id — Вычисляемый код Ребенка
Тогда, имея данные о Родителе, очередного Ребенка можем получить:
id = ((CH+1)^(LV-LEVEL-1)) * (COUNT_CHILDS+1) + ID
Ограничения
Все это хорошо, но целые числа не безграничны, и имеют вполне определенный диапазон. Например int32 может хранить 2^32=4 294 967 296 значений. Как это может повлиять на возможность применения этого метода?
Ответ — как всегда, всё зависит от текущей задачи. Но, смею предположить, для большинства задач, хватит.
Максимальное необходимое значение ключа, для хранения Элементов в такой структуре, можно найти по формуле:
(КоличествоДетей+1)^КоличествоУровней
Например, для 6-ти Уровней, при int32, можно позволить себе 39 Детей.
(39+1)^6 = 4 096 000 000
Как раз такое количество меня устраивало.
Меньше Уровней — будет больше Детей, и наоборот. Кому интересно — считайте сами, если результат меньше, чем максимальное допустимое у вас целое, то всё нормально.
Применения int64 значительно расширяет допустимые рамки. В этом случае для 6-ти Уровней доступны уже 1624 Ребенка. Скорость работы же с такими ключами замедлится не сильно (иногда и не замедлится вовсе).
Отряд не заметил потери бойца
Внимательный читатель увидит, что самый “левый” диапазон, пропадает для использования.
Например, в дереве, на Рис.2, не задействован диапазон чисел от 0 до 16. Можно, конечно, помудрить с начальным элементом (о нем речь далее) в алгоритмах. Но я не стал — хватает.
Начальный элемент
Для того, чтобы все это работало, в БД необходимо внести начальный элемент Дерева. Именно от него начнется “отсчет”. Я просто вношу его “руками” в таблицу. Как это будете делать вы — не важно, главное чтобы было понимание что делаете и зачем.
Итак, для всех, приведенных выше, иллюстраций, начальный элемент будет таким:
ID = 0
PARENT = 0
LEVEL = 0
COUNT_CHILDS = 0
Да, он не сверху, как принято это изображать. Он как бы “слева”. Но такой подход — работает, а это главное.
Знак ничего не меняет
Не все БД позволяют хранить беззнаковое целое. Но это абсолютно не влияет на алгоритмы. Как на вычисление нового Элемента, так и на выборку вложенных.
Вот наш пример, на котором Дерево «сдвинуто» в отрицательный диапазон:
![]()
Рис. 6
Для этого примера, начальный Элемент надо сделать таким:
ID = -32
PARENT = -32
LEVEL = 0
COUNT_CHILDS = 0
32-х разрядное целое позволяет хранить от -2 147 483 647 до 2 147 483 648
Хотим по “максимуму”, 6 Уровней при 39 Детях у каждого элемента.
Тогда получаем начальный id=-((39+1)^6)/2, и вручную в БД (или как захотите) вносим Группу со следующими значениями:
ID = -2,048,000,000
PARENT = -2,048,000,000
LEVEL = 0
COUNT_CHILDS = 0
Все будет работать так же хорошо.
Реализации алгоритма
Возможно, данный метод уже кем-то описывался и воплощался в жизнь.
Я, по причине своей темности, к сожалению, не читал. Все «выдумывал» сам.
В конце этой статьи, я дам ссылку на код, в котором работает весь механизм: вставка, перенос, удаление.
Далее описание ключевых моментов в алгоритмах.
Вставка нового элемента
Размерность дерева
CH — Допустимое количество Детей у каждого Элемента
LV — Допустимое количество Уровней в Дереве
Повторюсь, с этим надо определиться заранее. Как — читай статью заново.
Имеем запись о Родителе
ID — Integer
PARENT — Integer — ссылка на ID
LEVEL — Integer
COUNT_CHILDS — Integer
Тогда получить нового Ребенка можно по формуле:
id = ((CH+1)^(LV-LEVEL-1)) * (COUNT_CHILDS+1) + ID
Вставку не делаем, если Родитель не может [более] иметь Детей.
Перенос Элемента со всеми Детьми под другого Родителя
На самом деле все проще простого.
При переносе делаем изменения полей записи: id, parent, level, у самого элемента, и у всех возможных Детей. Делается все одним запросом.
Нам нужно:
1. Переносимый Элемент — K, конечно он у нас есть
2. Родитель — P, аналогично
3. НовыйРодитель — NP, это мы так же имеем
4. ДопустимоеКоличествоДетейВДереве -CH, оно у нас есть всегда — константа
5. Разница в уровнях — dL, вычисляется из уже имеющихся данных
Имея перечисленное, просто делаем UPDATE к элементу и ко всем его возможным детям, вычисляя новые ID по формуле:
Id = (K-P)*(CH+1)^dL+NP
Поле PARENT вычисляется аналогично, поле LEVEL меняем согласно dL.
Вот ключевой кусок из кода на django:
x_tmp = Group.objects.filter(id__gte=oldElement.id)
.filter(id__lt = limit_right)
.update(
id=((F('id')-id_departure)*((CH+1)**delta_level) + id_destination),
parent = ((F('parent')-id_departure)*((CH+1)**delta_level) + id_destination),
level = (F('level')-delta_level)
)
Подробнее — смотрите в примере, ссылка на который в конце данной статьи.
Перенос не делаем, если:
1. Новый Родитель не может [более] иметь Детей…
2. или… У переносимого Элемента есть Дети, которые окажутся “ниже” допустимого Уровня в Дереве. Такая ситуация возникнет только при переносе “вниз”. Как Вы ее обработаете, просто запретите перенос такого Элемента, или “обрежете” Детей до допустимого уровня — вам решать. Я перенос такого Элемента не делаю.
Удаление
Удаляю только Элемент, у которого нет Детей
При удалении элемента — уменьшаем КоличествоДетей у Родителя
Даже более написать нечего.
Вырыл яму — засыпай
Дети у каждого Родителя, представляют собой последовательность.
Может возникнуть ситуация, когда, в результате удаления или переноса, в этой последовательности образуется “дырка”. При наличии большого количества допустимых Детей, можно на это и забить. Но это не правильно. Поэтому, при удалении или переносе, необходимо отлавливать такие случаи и “переносить” на освободившееся место крайнего правого Ребенка.
Алгоритм здесь — частный случай вышеописанного Переноса. Только проще.
Область применения
Везде, где не нужна бесконечная иерархия.
а когда она нужна в прикладных повседневных задачах?
Минусы:
— Ограничение на количество Детей у Группы
— Ограничение на количество Уровней в Дереве
Некоторые варианты сочетания Детей и Групп для int32 и int64:
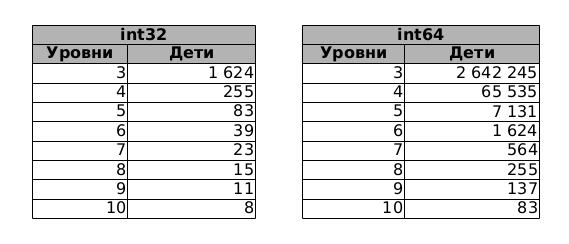
Рис.7
Может быть, гладя на эти цифры, кто-то решит, что не все уж так и плохо…
Плюсы:
— Скорость работы
— Небольшой объем данных
— Почти всегда можно обойтись одним запросом к диапазону ключей
— Простота реализации
Я не стал приводить сравнения с традиционными методами. По моему скромному мнению, если вышеперечисленные минусы не принципиальны, это один из лучших подходов, что можно использовать.
У кого есть желание — попробуйте сравнить.
Обещанный код
Не являюсь гуру ни в Python, ни в Django. Программирование сейчас это просто мое хобби. Тем не менее, даже мне удалось за сравнительно небольшое время получить код, работающий по описанным алгоритмам (это я написал для тех, кто ухмыльнулся при прочтении последнего из Плюсов :)).
Код, конечно, далек от совершенства, но он работает. Уверен, что в дальнейшем еще буду его править.
Профи же без труда его “почистят” и адаптируют под себя (и отловят возможные незамеченные баги). Привожу его здесь просто для демонстрации работы.
Спасибо, что уделили внимание.
Извиняюсь за возможные ошибки и опечатки.
Буду благодарен за любые комментарии.
PS
Я попытался рассказать о подходе, идее так сказать… На практике данный метод пока серьезно не проверен. Так же эта статья не о django (хоть и имеется реализация). Не затронуты вопросы обеспечения целостности данных (они и в других методах аналогичны). И много еще чего…
PPS
Если после прочтения, у кого-то появилось желание поставить минус, ставьте смело. Если не затруднит, «черкните» в комментах — с чем не согласны?
Автор: burdin






