
Данная статья является продолжением моей предыдущей статьи о детектировании движения на ПЛИС. В ней я хочу рассмотреть реализацию трёх алгоритмов фильтрации изображения, один из которых является наиболее важным при разработке детектора движения.
Необходимость применять фильтрацию вызвана шумами, присутствующими в кадре. Эти шумы имеют разную природу: одни вносит сама камера, другие вносят алгоритмы преобразования, третьи вносит окружающая среда, но все они создают нам препоны для детектирования объектов.
В данном проекте я столкнулся с шумами, которые вносит камера и алгоритмы бинаризации изображения (Background subtraction и Frame difference). Эти шумы проявляют себя в виде отдельных точек или их скопления как локально, так и по всему кадру. В зависимости от применяемого алгоритма обнаружения, они могут быть проигнорированы или приняты за объект.
Во избежание такого ложного обнаружения или сведения его вероятности к минимуму, мы и будем применять фильтрацию.
Медианный фильтр
Медианный фильтр, на мой взгляд, является наиболее значимым для подавления помех, с которыми мне пришлось столкнуться при разработке этого проекта. Он, как раз, подходит для устранения всякого рода мелких рассредоточенных вкраплений, однако он не является идеальным инструментом т.к. пропускает чуть более крупные области сосредоточенных помех.
Медианный фильтр представляет собой скользящие окно, в нашем случае, размерностью 3x3 пикселя. На вход он принимает 9 значений (пикселей), а на выход выдаёт одно. Работает медианный фильтр так: сортирует входные данные (пиксели) в порядке возрастания и выдаёт серединный результат (медиану).
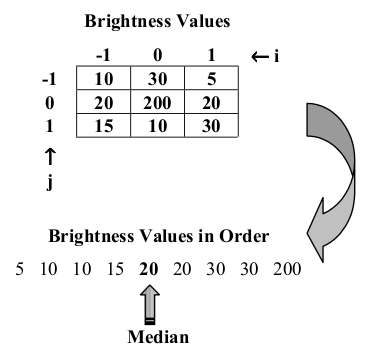
Данный алгоритм довольно просто реализуется на языке Си, но для ПЛИС его реализация несколько отличается. Функциональная классическая схема фильтра показана на рисунке ниже. Она состоит из 19-ти базовых элементов.
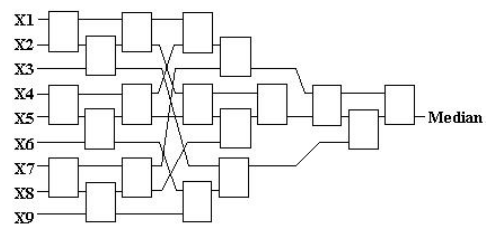
Каждый базовый элемент (узел) представляет собой компаратор и мультиплексор.
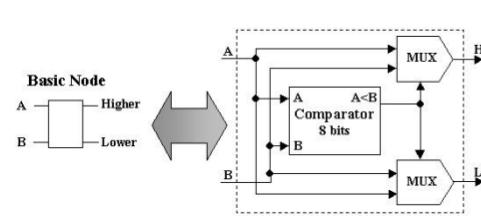
На языке Verilog это выглядит так:
module median_node
#(
parameter DATA_WIDTH = 8,
parameter LOW_MUX = 1, // disable low output
parameter HI_MUX = 1 // disable high output
)(
input wire [DATA_WIDTH-1:0] data_a,
input wire [DATA_WIDTH-1:0] data_b,
output reg [DATA_WIDTH-1:0] data_hi,
output reg [DATA_WIDTH-1:0] data_lo
);
wire sel0;
alt_compare cmp(
.dataa(data_a),
.datab(data_b),
.agb(sel0),
.alb()
);
always @(*)
begin : mux_lo_hi
case (sel0)
1'b0 :
begin
if(LOW_MUX == 1)
data_lo = data_a;
if(HI_MUX == 1)
data_hi = data_b;
end
1'b1 :
begin
if(LOW_MUX == 1)
data_lo = data_b;
if(HI_MUX == 1)
data_hi = data_a;
end
default :
begin
data_lo = {DATA_WIDTH{1'b0}};
data_hi = {DATA_WIDTH{1'b0}};
end
endcase
end
endmoduleВ качестве компаратора используется мегафункция alt_compare. Далее все узлы соединяются согласно схеме. Симуляция работы фильтра в ModelSim выглядит так:
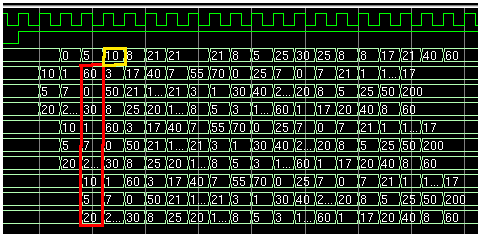
Красный прямоугольник — входные данные, жёлтый — выход фильтра. Выходной сигнал задержан на 1 такт т.к. Фильтр имеет синхронный регистровый выход.
Итак, с медианным фильтром всё понятно, осталось разобраться с окном 3x3.
Скользящее окно 3x3
Вот так оно выглядет в действии. Я себе это представляю не как окно скользит по картинке, а как картинка проходит сквозь статичное окно ), но сути это не меняет.

В ПЛИС окно делается не сложно, но требует 2 элемента FIFO размером в одну строку, в нашем случае 320 элементов. Выглядит это так:
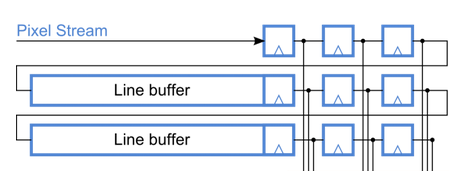
Нижний Line buffer — это строка 1, верхний Line buffer — строка 2, а данные строки 3 берутся прямо из потока когда оба FIFO заполнены по 320, в нашем случае, элементов.
На языке Verilog это сделано так:
wire [7:0] line3_data = data_in;
wire line2_empty;
wire line2_wr_rq = (data_in_en && !line2_data_ready);
wire line2_data_valid = !line2_empty;
wire line2_data_ready;
wire [7:0] line2_data;
wire [7:0] median_out_t, sobel_out_t, gaus_out_t;
reg [7:0] filter_out_r = 0;
// row 3 FIFO
alt_fifo_512x8 LINE2_FIFO (
.aclr(),
.clock(clk),
.data(line3_data),
.rdreq(line1_wr_rq),
.wrreq(line2_wr_rq),
.almost_full(line2_data_ready),
.empty(line2_empty),
.full(),
.q(line2_data),
.usedw()
);
wire line1_wr_rq = (line2_data_valid && !line1_data_ready);
wire line1_data_ready;
wire [7:0] line1_data;
// row 2 FIFO
alt_fifo_512x8 LINE1_FIFO (
.aclr(),
.clock(clk),
.data(line2_data),
.rdreq(line1_rd_rq),
.wrreq(line1_wr_rq),
.almost_full(line1_data_ready),
.empty(),
.full(),
.q(line1_data),
.usedw()
);
// median filter top
median_top
#(
.DATA_WIDTH(8)
) median_top (
.clk(clk),
.a0(a0),
.b0(b0),
.c0(c0),
.a1(a1),
.b1(b1),
.c1(c1),
.a2(a2),
.b2(b2),
.c2(c2),
.median(median_out_t)
);
Детектор Собеля
Детектор собеля представляет собой оператор, вычисляющий приблизительный градиент яркости. Как и медианный фильтр, детектор Собеля — это оконная, в нашем случае 3x3, функция с 9-ю входами и одним выходом. В классическом исполнении выходом данной функции является квадратный корень из суммы квадратов градиентов по осям X и Y. Результат работы детектора выглядит как белые контуры контрастных объектов на черном фоне.
Матрица коэффициентов фильтра:
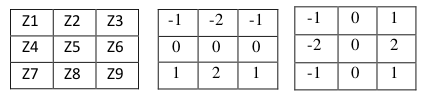
Градиент вычисляется методом свёртки значений пикселей с коэффициентами матрицы фильтра по формуле:
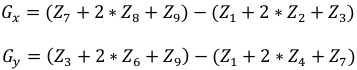
Как и в случае с медианным фильтром, нам нужно использовать формирование окна 3x3 пикселя для работы с этим фильтром:
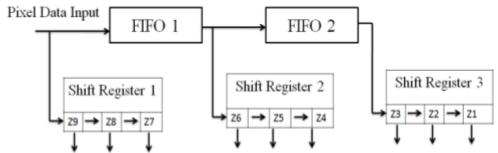
Shift register 1, 2 и 3 на функциональной схеме это запайплайненные входные данные из FIFO, на Verilog выглядит так:
reg [7:0] a0,b0,c0,a1,b1,c1,a2,b2,c2;
always @(posedge clk or negedge nRst)
if (!nRst) begin
a0 <= 8'd0; b0 <= 8'd0; c0 <= 8'd0;
a1 <= 8'd0; b1 <= 8'd0; c1 <= 8'd0;
a2 <= 8'd0; b2 <= 8'd0; c2 <= 8'd0;
end else begin
a0 <= line1_data;
b0 <= line2_data;
c0 <= line3_data;
//pipeline step 1
a1 <= a0;
b1 <= b0;
c1 <= c0;
//pipeline step 2
a2 <= a1;
b2 <= b1;
c2 <= c1;
endКод самого детектора очень прост:
module sobel_detector (clk,z0,z1,z2,z3,z4,z5,z6,z7,z8,edge_out);
input clk;
input [7:0] z0,z1,z2,z3,z4,z5,z6,z7,z8;
output [7:0] edge_out;
reg signed [10:0] Gx;
reg signed [10:0] Gy;
reg signed [10:0] abs_Gx;
reg signed [10:0] abs_Gy;
reg [10:0] sum;
always @ (posedge clk) begin
//original
//Gx<=((z2-z0)+((z5-z3)<<1)+(z8-z6)); //masking in x direction
//Gy<=((z0-z6)+((z1-z7)<<1)+(z2-z8)); //masking in y direction
// modified
Gx <= (z4-z3);
Gy <= (z4-z1);
abs_Gx <= (Gx[10]?~Gx+1'b1:Gx);//if negative, then invert and add to make pos.
abs_Gy <= (Gy[10]?~Gy+1'b1:Gy);//if negative, then invert and add to make pos.
sum <= abs_Gx+abs_Gy;
end
//Apply Threshold
assign edge_out = (sum > 20) ? 8'hff : 8'h00;
endmodule
sobel_detector sobel (
.clk(clk),
.z0(a0),
.z1(a1),
.z2(a2),
.z3(b0),
.z4(b1),
.z5(b2),
.z6(c0),
.z7(c1),
.z8(c2),
.edge_out(sobel_out_t)
);
Однако, при тестировании этого детектора выяснилось, что очень много шума идёт на его выход, и вместо красивого белого контура на черном фоне мы видим белые пятна. С чем связан такой результат я не понял, применение разных пороговых значений классического детектора не дало желаемого результата.
Заниматься поисками причины такого поведения детектора я не стал, т.к. данный детектор не представляет для меня практического интереса, только познавательный. Вместо этого я модифицировал матрицу оператора Собеля и получил приемлемый результат.
Классическая матрица:
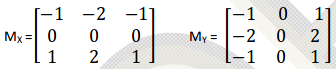
Модифицированная матрица:
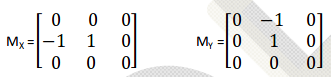
Фильтр Гаусса
Фильтр Гаусса, как и медианный фильтр, используется для устранения шума в кадре, однако у него есть и побочный эффект — размытие изображения. В нашем проекте нет такого шума, который нужно удалять фильтром Гаусса, поэтому реализация данного фильтра имеет исключительно академический интерес.
Как и два ранее рассмотренных фильтра, оператор Гаусса тоже является оконной функцией 3x3.
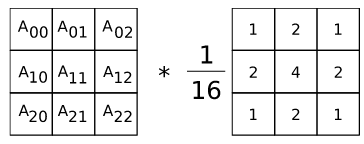
Схематично его реализация выглядит так:
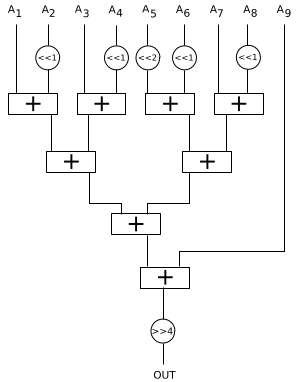
Код на языке Verilog:
module gaus_filter
#(
parameter DATA_IN_WIDTH = 8
)(
input wire [DATA_IN_WIDTH-1:0] d00_in,
input wire [DATA_IN_WIDTH-1:0] d01_in,
input wire [DATA_IN_WIDTH-1:0] d02_in,
input wire [DATA_IN_WIDTH-1:0] d10_in,
input wire [DATA_IN_WIDTH-1:0] d11_in,
input wire [DATA_IN_WIDTH-1:0] d12_in,
input wire [DATA_IN_WIDTH-1:0] d20_in,
input wire [DATA_IN_WIDTH-1:0] d21_in,
input wire [DATA_IN_WIDTH-1:0] d22_in,
output wire [DATA_IN_WIDTH-1:0] ftr_out,
);
wire [10:0] s1 = d00_in+(d01_in<<1)+d02_in+(d10_in<<1);
wire [10:0] s2 = (d11_in<<2)+(d12_in<<1)+d20_in+(d21_in<<1);
wire [11:0] s3 = s1+s2+d22_in;
assign ftr_out = s3>>4;
endmodule
gaus_filter
#(
.DATA_IN_WIDTH(8)
) gaus_filter_inst(
.d00_in (a0),
.d01_in (a1),
.d02_in (a2),
.d10_in (b0),
.d11_in (b1),
.d12_in (b2),
.d20_in (c0),
.d21_in (c1),
.d22_in (c2),
.ftr_out (gaus_out_t),
);
Входные значения фильтров
На вход медианного фильтра подаётся абсолютная разница кадров grayscale представления для его последующей фильтрации, в то время как на вход детектора Собеля и фильтра Гаусса подаётся само grayscale представление, а не его разница.
Выводы
Рассмотренные выше фильтры не были доведены до совершенства т.к. в этом не было нужды для данного проекта. При желании можно реализовать и использовать более сложные и ресурсоёмкие конструкции фильтров под конкретную задачу, а эта статья носит только ознакомительный характер.
Для дальнейшего развития этого проекта нам потребуется только медианный фильтр.
Демонстрация результата
На правой половине экрана попеременно отображаются разные режимы работы, обозначенные цветовыми маркерами (квадрат в углу изображения)
Черный — grayscale представление без фильтрации
Красный — разница кадров без фильтрации
Зелёный — разница кадров отфильтрованная медианным фильтром
Синий — детектор Собеля
Белый — фильтр Гаусса
Первый проход на видео — это работа алгоритма Frame difference. Фильтрация медианным фильтром не очень заметна на видео. Второй проход — Background subtraction. Здесь заметна разница между разницей без фильтрации и с фильтрацией — исчезли некоторые отдельные белые точки.
После фильтра Гаусса изображение сменяется на grayscale и становится заметна разница: с Гауссом изображение менее резкое чем просто grayscale.
Материалы
→ Median filter FPGA implementation
→ Sobel filter implementation
→ Gaussian filter on FPGA
Автор: ubobrov






