Сказал как-то раз Евклид, что параллельные линии не пересекаются. И назвал он это пятым постулатом. Жалко, что не вторым.
В этой статье я бы хотел перейти от сферических котов Шредингера в резонаторах Гельмгольца к чему-то более практичному, тем более, что Хабр интересуют физические реализации и применение квантовых компьютеров.
Тут я решил рассказать про составные системы и описать алгоритм Дойча.
Составные системы
Прежде чем приступать к алгоритму, хотелось бы рассказать про такую вещь, как составная система. Тот же регистр. Что такое регистр у обычного процессора, думаю, знают все. Чем же отличается обычный регистр от квантового? Квантовый регистр — это совокупность отдельных кубит. Квантовая механика гласит, что квантовое состояние системы описывается тензорным произведением квантовых состояний подсистем.
У нас есть кучка кубитов, которые находятся в разных состояниях |Ψ1>, | Ψ2>, |Ψ3> и т.п. Склепаем из них квантовый регистр, перемножив состояния по правилам тензорного произведения векторов:
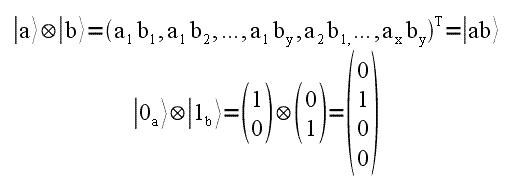
Вот такие вот состояния называются разложимыми. В то же время существуют запутанные состояния, иначе неразложимые, играющие роль в квантовой телепортации и сверхплотном кодировании. К этим запуткам можно отнести состояния Белла и ЭПР пары. Кстати, квантовую телепортацию успешно реализовали еще в 1997 году. А вот в 2010 китайцам удалось передать квантовое состояние фотона на 16 километров. Правда, копированием тут не пахнет, так как все равно первая частица разрушается.
Алгоритм Дойча
Это самый первый алгоритм, созданный для квантового компьютера. Что делает этот алгоритм? Всего лишь решает задачу Дойча, используя только одно вычисление. Это быстрее, чем на классическом компьютере, где пришлось бы выполнять как минимум два вычисления, а это быстрота достигается за счет квантового параллелизма.
Данный алгоритм был реализован на твердотельном ядерном магнитно-резонансном квантовом компьютере.
Что внутри?
Давайте глянем на схему компьютера, реализующего этот алгоритм:
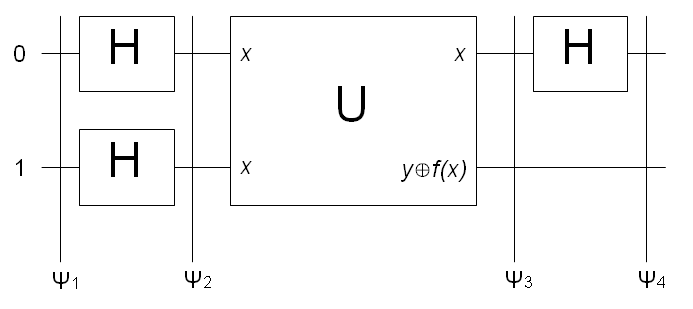
Предположим, что на вход этой машине судного дня подали два кубита — с значениями |0> и |1>, как вы видите на картинке. Что ожидает эти кубиты? Они сразу же попадают в вентиль Адамара и подвергаются там пыткам, превращаясь в интересную суперпозицию:
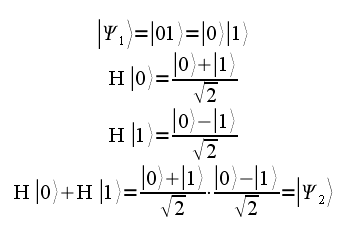
Что же дальше? А дальше оно идет в «черный ящик» U (они называются Оракулами) и там происходят некоторые преобразования, которые я решил опустить, в конце концов:
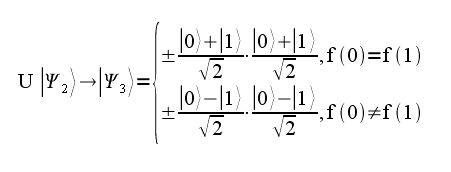
Первый выходной кубит проходит еще один вентиль Адамара:
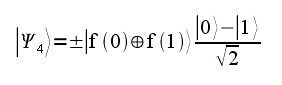
Чтобы решить задачу, нам нужно узнать значение выражения f(0) ⊕ f(1), то есть глобальное свойство функции. Как вы видите, в одном кубите есть значения и f(0), и f(1)! В этом и заключается удивительное свойство квантового параллелизма. Если выходное состояние первого кубита |0>, функция является константой. Иначе — нет.
Вот коротенькая статья и подходит к концу. Надеюсь, было интересно и понятно. Если вдруг я допустил какие-то ошибки — просьба сообщать о них в личку.
Автор: holmuk