Задачи о переборе всех возможных перестановок заданного множества сущностей возникают в программировании достаточно часто. Как известно из комбинаторики, число возможных перестановок n предметов равно попросту факториалу числа n
n! = n * (n — 1) * (n – 2) * … * 3 * 2 * 1
Факториал – достаточно быстро растущая функция, об этом говорит ее асимптотика (формула Стирлинга), хотя достаточно посмотреть на факториалы нескольких первых членов натурального ряда:
1! 1
2! 2
3! 6
4! 24
5! 120
6! 720
7! 5 040
8! 40 320
9! 362 880
10! 3 628 800
11! 39 916 800
12! 479 001 600
13! 6 227 020 800
14! 87 178 291 200
15! 1 307 674 368 000
Как видно, факториал 13-ти уже не умещается в тип данных long.
Если задаться целью найти однозначное соответствие между номером перестановки — числом в диапазоне от 1 до n! – и ее реализацией, можно натолкнуться на один очень интересный математический факт.
Для начала вспомним понятие позиционной системы счисления. Вклад каждого разряда числа в его значение в позиционной системе по основанию K есть разряд, умноженный на основание K в степени, равной позиции разряда в записи числа. Основание системы счисления обычно пишут как подстрочный индекс, таким образом
196610 = 1*103 + 9 * 102 + 6 * 101 + 6 (*100)
101100012 = 1 * 27 + 0 * 26 + 1 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20 (=17710)
Позиционная запись, помимо компактности, обладает тем бесценным свойством, что алгоритм выполнения арифметических операций оказывается чрезвычайно простым (есть историческая байка, что в школах средневековья изучение арифметики занимало несколько лет, поскольку вычисления над числами в НЕпозиционной римской записи имели множество правил для того, чтобы провести простое сложение!)
Оказывается, существует, и является однозначным разложение и способ записи числа, в котором каждый разряд в таком его представлении умножается на ФАКТОРИАЛ номера позиции.
Покажем это на примерах:
1985 = 2 * 6! + 4 * 5! + 0 * 4! + 2 * 3! + 2 * 2! + 1 * 1!
2 940 861 129 405 = 2*15! + 3*14! + 10*13! + 3*12! + 6*11! + 8*10! + 4*9! + 8*8! + 0*7! + 2*6! + 2*5! + 1*4! + 3*3! + 1*2! + 1*1!
В обычной позиционной системе значение каждого разряда должно быть строго меньше основания. В факториальной же системе каждый «разряд» меньше либо равен основанию факториала, перед которым он стоит. При этом действуют обычные для сложения правила переноса разряда при переполнении.
Более математически строго: каждое натуральное число n можно единственным образом представить в виде следующей суммы
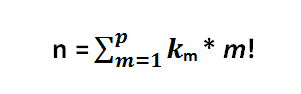
где
km <= m – коэффициент при m! — он же разряд числа в его факториальном представлении,
p – количество «разрядов» в числе в его факториальном представлении
то есть число записывается как kp kp-1 kp-2… k2 k1
Теперь опишем, как использовать факториальное представление (разложение) числа для генерации соответствующей перестановки. Расположим n элементов в порядке возрастания индекса от 1 до n. Для каждого числа в диапазоне 0..n!-1 произведем факториальное разложение, вычислив его коэффициенты km. В разложении нуля коэффициенты km будут все нули, в разложении числа n!-1 все km = m, m меняется в диапазоне от 0 до n-1. Теперь поместим элемент с номером m на место с номером km+1, считая лишь свободные места, оставшиеся к этому шагу. Фактически, эта процедура повторяет рассуждения, которые приводятся при вычислении числа возможных перестановок из n элементов – первый элемент может быть размещен n способами, второй – (n-1) способом и так далее. Таким образом, мы получим все возможные перестановки из n несовпадающих элементов.
Проиллюстрируем это для 5 предметов (120 вариантов перестановок) и перестановки №77
77 = 3 * 4! + 0 * 3! + 2 * 2! + 1 * 1!

Не являясь программистом-практиком, я все же выскажу предположения (теоретические)), как можно было бы использовать подобное разложение. Можно разбить общее число возможных перестановок на поддиапазоны по числу имеющихся параллельных потоков исполнения, и извлекать текущую перестановку прямо из представления переменной цикла в факториальной записи. Разложение в факториальную форму – задача достаточно вычислительно сложная, но можно разложить только стартовое число поддиапазона, а затем просто прибавлять единицу, перенося ее в следующий разряд в случае переполнения.
Автор: vkomen





