При решении задач с применением методов машинного обучения, как правило, мы выбираем наиболее подходящий алгоритм в контексте задачи, а также способ настройки его параметров.
Давайте рассмотрим несколько иной подход: вместо того, чтобы самостоятельно выбирать алгоритм, разработаем программу, которая способна автоматически генерировать алгоритмы для решения задач.
Стохастический метод конструирования программ, основанный на использовании генетического алгоритма — называется генетическим программированием.
Несколько слов о генетическом алгоритме
Генетический алгоритм – это метод оптимизации, в основе которого лежит идея естественного отбора как средства достижения наилучшего результата. Обобщённость формулировки предоставляет возможность использовать этот алгоритм для решения разнообразных задач. Всё что нужно, это:
- придумать каким образом решение задачи можна закодировать в виде хромосом, которые обладают способностью мутировать и скрещиваться
- определить функцию приспособленности, которая вычесляет насколько оптимальным является решение закодированное той или иной хромосомой
- имея начальную популяцию хромосом и функцию приспособленности, с помощью генетического алгоритма можно отыскать хромосомы, которые соответсвуют оптимальным решениям задачи
Конечно, генетическому алгоритму присущи определенные недостатки, связанные с его стохастической природой, но исходя из собственного опыта, могу заключить что он находит приемлемые решения в условиях ресурсо-временных ограничений.
Генетическое программирование и символьная регрессия
Предлагаю подробнее рассмотреть концепцию генетического программирования на примере символьной регрессии — задачи нахождения формулы, которая описывает некую зависимость. Более формально, её можно сформулировать как построение регрессионной модели в виде суперпозиции заданных функций.
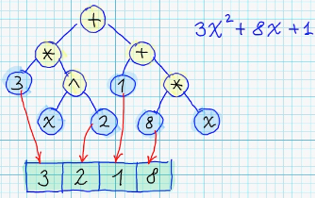
Достаточно удобным вариантом представления программы является синтаксическое дерево. В данном случае роль «программ» играют алгебраические формулы. Листовые узлы соответствуют переменным или числовым константам, а нелистовые узлы содержат операцию, которая выполняется над дочерними узлами.
Пример синтаксического дерева:
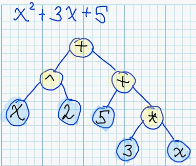
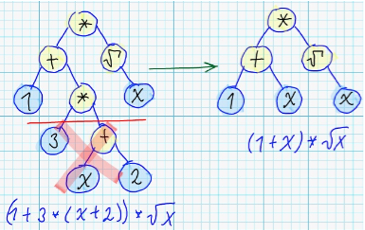
Стоит заметить, что для каждого синтаксического дерева существует бесконечное количество семантически эквивалентных деревьев, например:
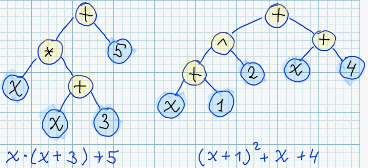
Мы будем использовать синтаксические деревья в качестве хромосом.
Генетические операции над синтаксическими деревьями
Скрещивание можно реализовать путем обмена случайно выбранных поддеревьев:
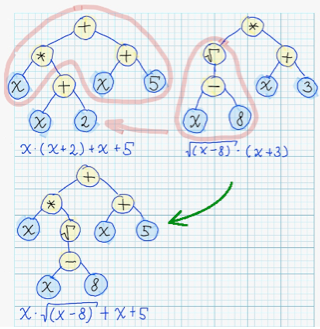
Мутаций можно придумать много различных вариантов, но в конечном счёте, в своей реализации я остановился на следующих:
- Замена функции на случайно выбранную другую:
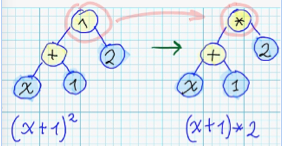
- Замена поддерева на случайно сгенерированное поддерево:
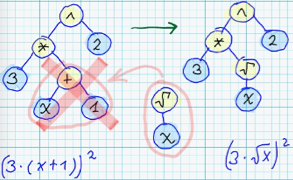
- Удаление промежуточного нелистового узла:
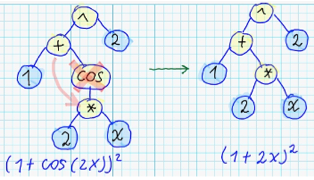
- Создание случайного узла, который назначается новым корнем дерева:
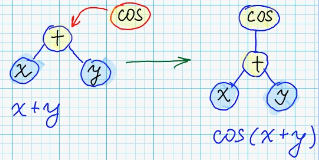
- Для узлов с некоммутативными операциями — перестановка местами дочерних поддеревьев:
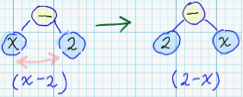
Функция приспособленности синтаксического дерева вычисляет насколько хорошо соответствующая алгебраическая формула аппроксимирует данные, и, фактически, являет собой сумму квадратов отклонений значений сгенерированной функции от тренировочных данных.
Начальная популяция являет собой набор случайно сгенерированных синтаксических деревьев.
Оптимизации
В общем — описанных операций скрещивания и мутации должно быть достаточно для отыскания решения. Но, исходя из своего опыта, могу сказать, что в таком случае — более-менее приемлемое решение будет находится достаточно долго. Поэтому, опишу несколько оптимизаций, которые ускоряют поиск решений.
- Давайте рассмотрим две формулы, созданные в процессе поиска решений (красные крестики — это тренировочные данные):

Легко заметить, что синяя прямая находится вцелом довольно близко к тренировочным данным, в отличие от зеленой параболы — а значит, имеет меньшую сумму квадратов отклонений относительно тренировочной выборки.Но, с другой стороны, невооруженным глазом видно что парабола — как раз то что нам нужно.
Все дело в коэффициентах. Как вы, возможно, уже догадались — коэффициенты каждого дерева оптимизируются. А для оптимизации коэффициентов, конечно же, используется генетический алгоритм!
В данном случае хромосомой является массив чисел:
- Поскольку мы работаем только с действительными числами — удобно оперировать функциями, в которых область значений является подмножеством области определения, например:
+, -, sin(x), cos(x), ln(abs(x) +0.00001), sqrt(abs(x)) и т.д.
Таким образом — в результате выполнения генетических модификаций мы будем гарантированно получать синтаксические деревья, не содержащие ошибок.
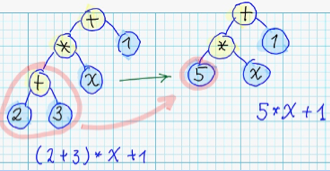
- Бывают комбинации, в которых какое-либо поддерево содержит листовые узлы только с числовыми константами. Можно рассчитать его значение и упростить синтаксическое дерево:
- Еще одна оптимизация заключается в ограничении максимальной глубины дерева (конечно, это накладывает свои ограничения на пространство поиска решений, но необходимость этой оптимизации продиктована практическими соображениями):
- Для избежания ситуации, когда все деревья в популяции похожи друг на друга (генетический алгоритм застрял в локальном минимуме) — есть ненулевая вероятность полной замены одного из деревьев на случайно сгенерированное.
Достаточно теории, посмотрим как это работает на практике
Давайте попробуем отыскать формулу, которая будет удовлетворять следующую закономерность:
| x | y | z | f(x, y, z) |
| 26 | 35 | 1 | 830 |
| 8 | 24 | -11 | 130 |
| 20 | 1 | 10 | 477 |
| 33 | 11 | 2 | 1217 |
| 37 | 16 | 7 | 1524 |
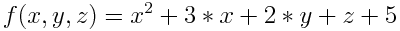
На 111 итерации получаем формулу:
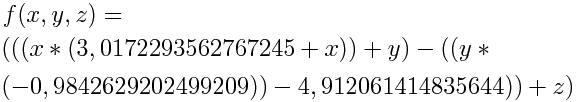
Которая после преобразований превращается в формулу, что почти совпадает с искомой:
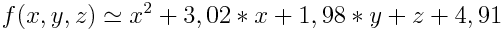
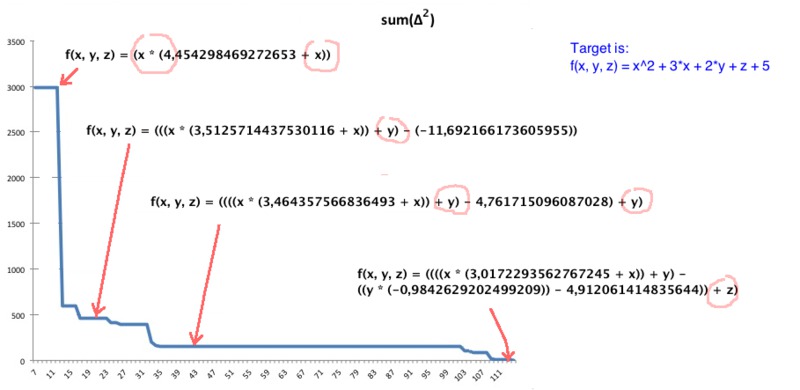
Ниже изображена динамика формирования решения:
| № Популяции | Сумма квадратов отклонений | Лучшая формула |
|---|---|---|
| 0 | 1669012.26766007 | f(x, y, z) = 544,6859000804278 |
| 1 | 169681.53834698 | f(x, y, z) = (x * (28,961135980737247 + z)) |
| 2 | 148288.46850717001 | f(x, y, z) = (x * (31,37500136808971 + z)) |
| 3 | 132767.659539771 | f(x, y, z) = (x * (52,43484580560726 + (-16,667350145606648))) |
| 4 | 2985.09234959275 | f(x, y, z) = (x * (4,433746792798393 + x)) |
| 5 | 2983.6495099344102 | f(x, y, z) = (x * (4,4641060233894825 + x)) |
| 6 | 2983.6495099344102 | |
| 7 | 2983.3906931086399 | f(x, y, z) = (x * (4,454265913806434 + x)) |
| 8 | 2983.3906931086399 | |
| 9 | 2983.3904005863701 | f(x, y, z) = (x * (4,454298469272653 + x)) |
| 10 | 597.81897366597798 | f(x, y, z) = ((x * (3,844350383063788 + x)) + y) |
| 11 | 594.94169424631298 | f(x, y, z) = ((x * (3,8969889609817003 + x)) + y) |
| 12 | 594.94169424631298 | |
| 13 | 593.73658852479002 | f(x, y, z) = ((x * (3,882218261498 + x)) + y) |
| 14 | 465.83708126862598 | f(x, y, z) = (((x * (4,005216664324722 + x)) + y) — z) |
| 15 | 465.83708126862598 | |
| 16 | 465.83708126862598 | |
| 17 | 465.83708126862598 | |
| 18 | 465.83015734565402 | f(x, y, z) = (((x * (4,005911869833458 + x)) + y) — z) |
| 19 | 465.83015734565402 | |
| 20 | 465.83015734565402 | |
| 21 | 415.16018053718898 | f(x, y, z) = (((x * (3,5125714437530116 + x)) + y) — (-11,692166173605955)) |
| 22 | 415.16018053718898 | |
| 23 | 395.52399773897002 | f(x, y, z) = (((x * (3,382514048684854 + x)) + y) — (-14,647402701410202)) |
| 24 | 395.07066142434297 | f(x, y, z) = (((x * (3,3745415764367164 + x)) + y) — (-14,718709944856545)) |
| 25 | 394.26327346841998 | f(x, y, z) = (((x * (3,3648511983617673 + x)) + y) — (-15,239602399729787)) |
| 26 | 392.88638158772301 | f(x, y, z) = (((x * (3,337209019532033 + x)) + y) — (-15,802043204356028)) |
| 27 | 392.32411284414297 | f(x, y, z) = (((x * (3,3064294470317237 + x)) + y) — (-16,587523294477112)) |
| 28 | 392.32411284414297 | |
| 29 | 392.32411284414297 | |
| 30 | 201.31809082052899 | f(x, y, z) = ((((x * (3,1436791342095485 + x)) + y) — (-3,592869973372564)) + y) |
| 31 | 164.61977693577799 | f(x, y, z) = ((((x * (3,284782293612155 + x)) + y) — 0,2814995918777923) + y) |
| 32 | 149.279581721206 | f(x, y, z) = ((((x * (3,428687042834285 + x)) + y) — 3,8492278595932117) + y) |
| 33 | 149.278346415192 | f(x, y, z) = ((((x * (3,428687042834285 + x)) + y) — 3,8397689886934776) + y) |
| 34 | 149.278346415192 | |
| 35 | 148.94429071530399 | f(x, y, z) = ((((x * (3,4733961096640367 + x)) + y) — 4,871582132520638) + y) |
| 36 | 148.94429071530399 | |
| 37 | 148.92149057538799 | f(x, y, z) = ((((x * (3,4733961096640367 + x)) + y) — 4,927910435311452) + y) |
| 38 | 148.842647569717 | f(x, y, z) = ((((x * (3,4667603760518504 + x)) + y) — 4,761715096087028) + y) |
| 39 | 148.842126194348 | f(x, y, z) = ((((x * (3,4667603760518504 + x)) + y) — 4,766164660321495) + y) |
| 40 | 148.83482158482201 | f(x, y, z) = ((((x * (3,464357566836493 + x)) + y) — 4,761715096087028) + y) |
| 41 | 148.83482158482201 | |
| 42 | 148.83482158482201 | |
| 43 | 148.83482158482201 | |
| 44 | 148.83482158482201 | |
| 45 | 148.824714357071 | f(x, y, z) = ((((x * (3,464357566836493 + x)) + y) — 4,723957086860974) + y) |
| 46 | 148.824474980844 | f(x, y, z) = ((((x * (3,464357566836493 + x)) + y) — 4,719858152218609) + y) |
| 47 | 148.824474980844 | |
| 48 | 148.824474980844 | |
| 49 | 148.824474980844 | |
| 50 | 148.82441313535 | f(x, y, z) = ((((x * (3,464357566836493 + x)) + y) — 4,717481429398491) + y) |
| 51 | 148.82441154759999 | f(x, y, z) = ((((x * (3,464357566836493 + x)) + y) — 4,717364268937347) + y) |
| 52 | 148.82441154759999 | |
| 53 | 148.82441154759999 | |
| 54 | 148.82441154759999 | |
| 55 | 148.82441154759999 | |
| 56 | 148.82441154759999 | |
| 57 | 148.82441154759999 | |
| 58 | 148.824403242995 | f(x, y, z) = ((((x * (3,464357566836493 + x)) + y) — 4,715925249764239) + y) |
| 59 | 148.824403242995 | |
| 60 | 148.824403242995 | |
| 61 | 148.824403242995 | |
| 62 | 148.824403242995 | |
| 63 | 148.824403242995 | |
| 64 | 148.824403242995 | |
| 65 | 148.824403242995 | |
| 66 | 148.824403242995 | |
| 67 | 148.824403242995 | |
| 68 | 148.824403242995 | |
| 69 | 148.824403242995 | |
| 70 | 148.824403242995 | |
| 71 | 148.824403242995 | |
| 72 | 148.824403242995 | |
| 73 | 148.824403242995 | |
| 74 | 148.824403242995 | |
| 75 | 148.824403242995 | |
| 76 | 148.824403242995 | |
| 77 | 148.824403242995 | |
| 78 | 148.824403242995 | |
| 79 | 148.824403242995 | |
| 80 | 148.824403242995 | |
| 81 | 148.824403242995 | |
| 82 | 148.824403242995 | |
| 83 | 148.824403242995 | |
| 84 | 148.824403242995 | |
| 85 | 148.824403242995 | |
| 86 | 148.824403242995 | |
| 87 | 148.824403242995 | |
| 88 | 148.824403242995 | |
| 89 | 148.824403242995 | |
| 90 | 148.824403242995 | |
| 91 | 148.824403242995 | |
| 92 | 148.824403242995 | |
| 93 | 148.824403242995 | |
| 94 | 148.824403242995 | |
| 95 | 148.824403242995 | |
| 96 | 148.824403242995 | |
| 97 | 148.824403242995 | |
| 98 | 148.824403242995 | |
| 99 | 148.824403242995 | |
| 100 | 109.738448314378 | f(x, y, z) = ((((x * (3,6304822654527666 + x)) + y) — ((y * 0,26890083188968594) — (-4,125304601214528))) + y) |
| 101 | 109.738448314378 | |
| 102 | 86.7213316804214 | f(x, y, z) = ((((x * (3,454146360987013 + x)) + y) — ((y * 0,26890083188968594) — 0,31706243101113074)) + y) |
| 103 | 86.077603952275396 | f(x, y, z) = ((((x * (3,4532441079663054 + x)) + y) — ((y * 0,2821822285682245) — 0,5330637639727107)) + y) |
| 104 | 84.787024859776594 | f(x, y, z) = ((((x * (3,418583927986026 + x)) + y) — ((y * 0,30109799837668216) — 1,6913597460963947)) + y) |
| 105 | 84.787024859776594 | |
| 106 | 19.436528477129301 | f(x, y, z) = ((((x * (3,1298089197766688 + x)) + y) — ((y * (-1,1430183282239135)) — (-0,7601011336523038))) + z) |
| 107 | 9.2899337994931397 | f(x, y, z) = ((((x * (3,1298089197766688 + x)) + y) — ((y * (-0,9847117571207198)) — 2,01456442176615)) + z) |
| 108 | 9.2899337994931397 | |
| 109 | 8.5880221046539802 | f(x, y, z) = ((((x * (3,1002105039045555 + x)) + y) — ((y * (-0,9847117571207198)) — 2,01456442176615)) + z) |
| 110 | 8.5880221046539802 | |
| 111 | 0.38510898634568402 | f(x, y, z) = ((((x * (3,0172293562767245 + x)) + y) — ((y * (-0,9842629202499209)) — 4,912061414835644)) + z) |
Интересно проследить за этапами формирования решения:
- вначале находится зависимость от переменной x (на рисунке данный этап не показан, поскольку величина ошибки всё ещё очень большая — примерно 130000)
- затем формула трансформируется в квадратическую зависимость от х (сумма квадратов отклонений ~3000)
- после чего идентифицируется зависимость от переменной y (сумма квадратов отклонений ~500)
- и наконец, после оптимизации числовых параметров и идентификации зависимости от переменной z достигается оптимальный результат.
Ещё один пример
Иногда получаются формулы, которые не так очевидны. Например, однажды, при попытке получить формулу 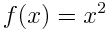 я получил следующий результат:
я получил следующий результат:
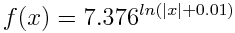
Но если воспользоватся тождеством:
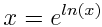
Можно показать что полученная формула правильная:
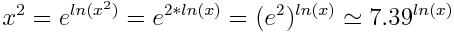
Если у Вас есть желание поэкспериментировать
Консольная утилита
- У вас должна быть установлена среда выполнения Java
- Скачайте отсюда файл symbolic_regression_1.0.jar
- В том же каталоге, где находится symbolic_regression_1.0.jar, создайте файл (например data.txt) следующего содержания:
# allowed functions are: ADD SUB MUL DIV SQRT POW LN SIN COS
# set which functions to use:
ADD MUL SUB# looking for:
f(x, y, z) — ?# define training set:
f(26, 35, 1) = 830
f(8, 24, -11) = 130
f(20, 1, 10) = 477
f(33, 11, 2) = 1217
f(37, 16, 7) = 1524 - Запустить поиск решения:
java -jar symbolic_regression_1.0.jar data.txtРешение считается найденным, если сумма квадратов отклонений меньше 10. Если решение ещё не найдено, то после каждых 50 итераций у Вас будет спрашиваться, хотите ли Вы продолжить.
Java программисты
Вы можете найти исходный код здесь: github.com/lagodiuk/genetic-programming
Вместо заключения
На довольно ограниченном количестве формул, которые я успел проверить, получались неплохие результаты, ещё были успешные эксперименты по отысканию первообразных и производных.
Также генетическое программирование можно довольно успешно применять для автоматического конструирования нейронных сетей (здесь небольшая демка приложения, в котором я реализовал данный подход).
Ещё есть идея — применить подобный подход (совместно с методиками QSAR) для автоматического конструирования структур химических соединений с заданными свойствами.
Литература
В Сети можно найти много материалов по тематике генетического программирования.
Отдельно хочу отметить следующие источники:
- Toby Segaran, Programming Collective Intelligence
- Сайт создателя концепции генетического программирования
Автор: stemm
