Недавно, на хабрахабре была опубликована статья, целиком и полностью посвященная диаграммам Вороного. В статье автор подробно описывает алгоритм Форчуна, применяемый для построения Диаграммы Вороного за O(n*log(n)). Стоит отметить, что описание этого алгоритма ни раз появлялось в рунете, в то время как о других алгоритмах (с той же асимптотикой) рассказано ровным счетом ничего. Данная статья исправляет это недоразумение, а также является отличным дополнением к уже опубликованному ранее материалу.
Ниже я расскажу о алгоритме 'разделяй и властвуй' построения диаграммы Вороного за O(n*log(n)), а также, основываясь на своем практическом опыте, о по-настоящему крутых штуках, в которых это применимо. Вообще, алгоритмы типа 'разделяй и властвуй' являются своего рода классикой программирования (думаю, про сортировку данным методом слышал каждый программист), хорошо параллелятся и легко читаются (если, конечно, знать основную идею алгоритма).
Описание алгоритма 'разделяй и властвуй' построения диаграммы Вороного
Исходное множество точек сортируется по одной из координат(положим, x) и делится на два, примерно равных множества. Каждое из полученных множеств снова делится на два и так происходит до тех пор, пока в каждом из множеств останется не более двух точек. Легко видеть, что таких разбиений будет не более чем log(n). Далее, для каждого полученного множества строятся диаграммы Вороного, после чего, в порядке обратном делению, эти диаграммы объединяются в одну. Полученная диаграмма Вороного и будет конечным результатом.
Чтобы описанный алгоритм имел сложность порядка O(n*log(n)), необходимо выполнять процесс объединения двух диаграмм Вороного за O(N). Отмечу, что для множества из двух точек, диаграммой Вороного будет являться серединный перпендикуляр отрезка образованного этими двумя точками.
Положим, что все точки отсортированы по X координате, а исходное множество разделено на два и для каждого построена диаграмма Вороного. Выполним объединение данных множеств и их диаграмм следующим образом:
⦁ 1. Для каждого из подмножеств найдем выпуклую оболочку (заметим, что построение выпуклой оболочки для каждого из множеств можно выполнять все тем же 'разделяй и властвуй': то есть, на каждом шаге объединения диаграмм Вороного мы объединяем и выпуклые оболочки данных множеств за O(N))
⦁ 2. Теперь, когда у нас есть две выпуклые оболочки исходных множеств, найдем 'верхнюю и нижнюю' границы данных множеств: то есть, мы должны найти два таких отрезка, которые объединяют две данные выпуклые оболочки в одну (естественно, выпуклую). Таким образом мы выполним условия шага 1, а также получим инициализирующие значения для шага 3. Данный шаг, как я и писал, можно выполнить за O(N).
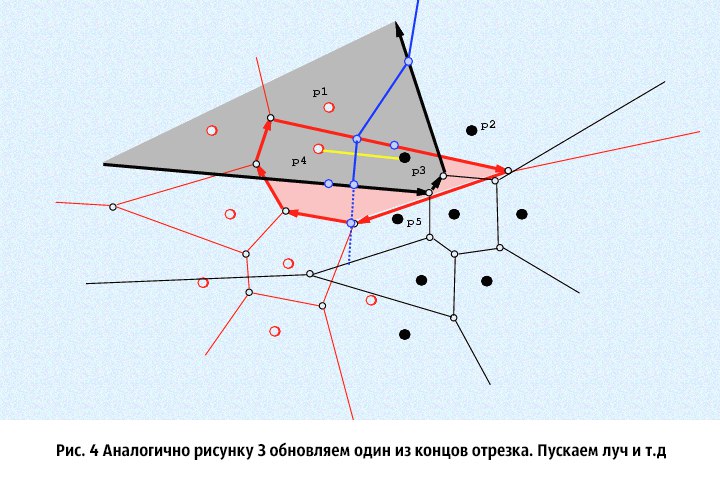
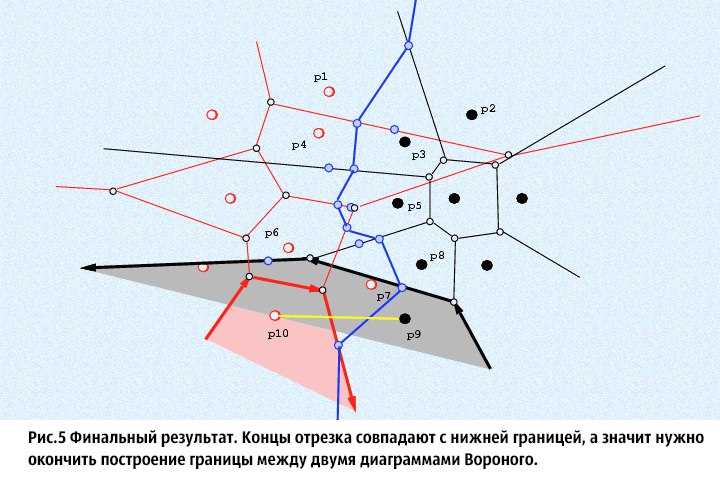
⦁ 3. Из полученных отрезков на шаге 2, выберем любой и обозначим за L (оставшийся обозначим за Q), и через его середину, перпендикулярно пускаем бесконечный луч. Представим, что данный луч только входит в исходное множество, и найдем его пересечения с ячейками диаграмм Вороного исходных множеств (считается, что луч простирается вперед, то есть у него есть направление). Мы пересекаем луч только с теми ячейками Вороного, центрами которых являются концы отрезка, перпендикулярно которому мы пускаем луч. Нам нужно найти точки пересечения данного луча с соответствующими ячейками Вороного и выбрать среди них ту, что пересекается раньше. Обозначим эту точку за M, а ячейку которую мы пересекли запомним и обозначим V. Далее, сделаем следующее: тот конец отрезка L, что является центром для не пересеченной ячейки Вороного оставляем в покое, а вот тот, что был центром ячейки которую мы пересекли — обновляем: мы пересекли одну из сторон ячейки Вороного, тогда новым концом отрезка L станет центр ячейки Вороного, смежной по этой стороне с пересеченной ячейкой. В специальное множество S (в нем хранится граница двух Диаграмм Вороного) надо добавить ту часть луча, которая простирается до пересечения со стороной ячейки. Повторяем шаг 3 до тех пор, пока значения концов отрезка L, не станут равны значениям концов отрезка Q. В итоге, в множестве S окажется непрерывный ломаный луч. Доказательство многих фактов, приведенных здесь (например, непрерывность луча в множестве S), можно найти в [1].
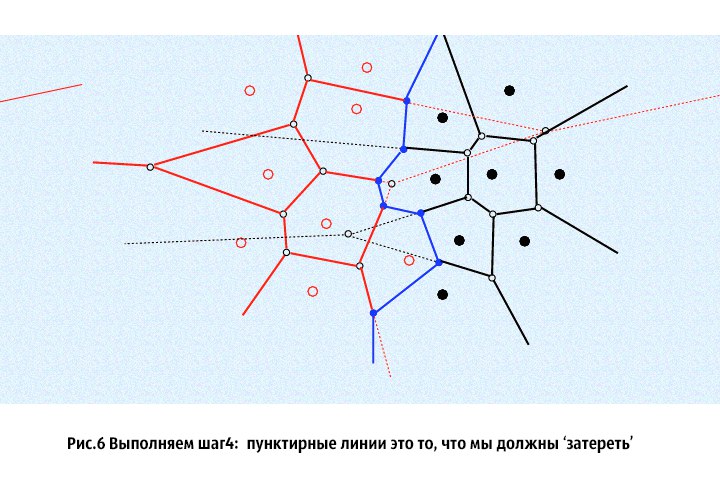
⦁ 4. Мы получили множество S, которое представляет собой непрерывный ломаный луч. Этот луч является границей, соединяющей диаграммы Вороного двух множеств. Для получения финального результата, нужно для диаграммы Вороного левого множества 'затереть' те отрезки что находятся справа от полученного луча, а для диаграммы Вороного правого множества 'затереть' те что слева. Сделать это быстро не проблема: когда мы пересекаем ячейку лучом, то очевидно, что сначала луч будет в неё входить, а затем, в какой-то определенный момент-выйдет. Нам нужно 'отловить' эти события, и в зависимости от того с диаграммой какого множества мы работаем(левого или правого), удалить левую или правую цепочки ребер ячейки Вороного, которую мы пересекли лучом, и добавить туда нужную часть из множества S.
Описанный выше алгоритм сложно понять без хорошей иллюстрации(картинки были взяты здесь):
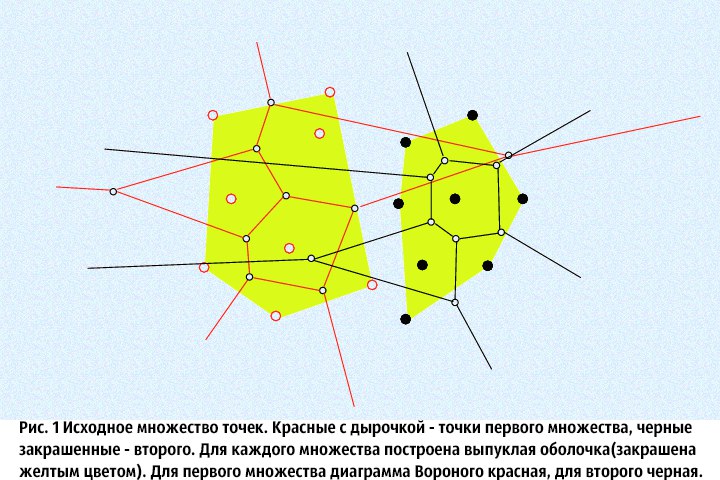
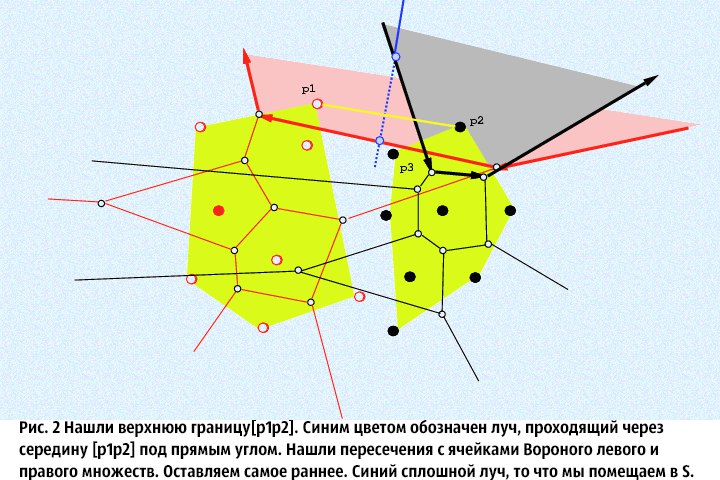
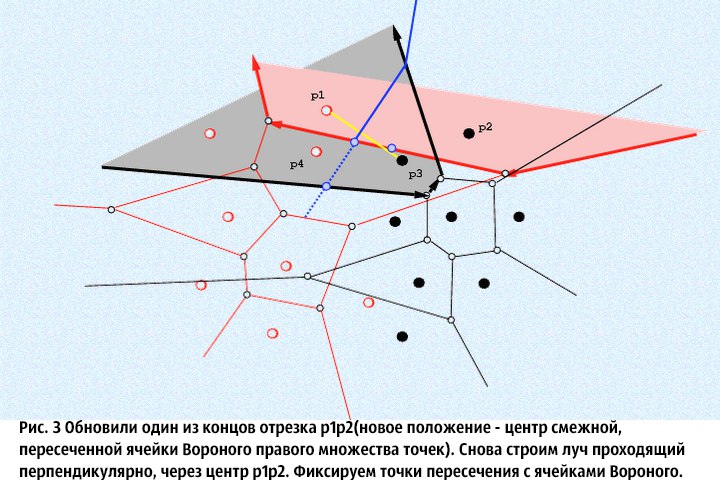
Ну и закончу этот подраздел публикации на том, что если точки имеют одинаковую координату X, то стоит их сортировать по координате Y, таким образом, чтобы равномерно и последовательно их разделить.
Применение Диаграммы Вороного — релаксация Ллойда
Релаксация Ллойда — один из удивительных и 'залипательных' алгоритмов, в котором активно используется построение диаграмм Вороного. Опишу сам алгоритм:
⦁ 1. Строим диаграмму Вороного для исходного множества точек, формируем ячейки Вороного.
⦁ 2. Находим «Центр Масс» каждой ячейки Вороного (сумма координат вершин ячейки Вороного, деленная на их количество).
⦁ 3. Сдвигаем центр каждой ячейки Вороного в позицию рассчитанного «Центра Масс».
⦁ 4. Повторяем данную процедуру N раз: до тех пор, пока расстояние сдвига не станет близким к нулю.
Что же мы получаем в итоге? Результат можно увидеть на этих двух коротких видео:
Выглядит красиво, но немного бесполезно !? Далеко нет!
На моем практическом опыте, релаксация Ллойда применялась в 3D моделировании: в так называемом «ремешинге сетки». То есть, дана сетка (обычно после обработки дешевеньким китайским сканером) и стоит задача полученную 'мешанину' треугольников превратить в нечто красивое и живое: в то, на чем можно производить более-менее точные вычисления(расчет 'кривизны сетки', аппроксимация точек триангуляционной сетки бесконечно гладкими поверхностями и т.п), стараясь не сильно отклониться в точности от оригинальной 'сканерной' сетки (более того, эта точность задается пользователем, а такой 'ремешинг' называется адаптивным (adaptive). Существует еще 'ремешинг' униформный (uniform) — здесь, задается не отклонение, а желаемая длина ребра в треугольнике). Я немного заговорился и забыл объяснить, что же мы понимаем под словом 'красивая' сетка. Сетку назовем 'красивой', если по своей структуре она состоит преимущественно из равносторонних треугольников, а валентность каждой вершины у такой сетки 6 (если вершина внутренняя, ну т.е 360. / 6. = 60 deg. — градус угла равностороннего треугольника) или 4 (если вершина лежит на открытом ребре, то есть треугольников с данной вершиной 3). Ну, и одним из важных этапов получения такой сетки является построение диаграммы Вороного и использование релаксации Ллойда. Собственно, получаем что-то в этом духе(аккуратно, картинки большие !):

После:

А теперь и до и после на одном изображении:
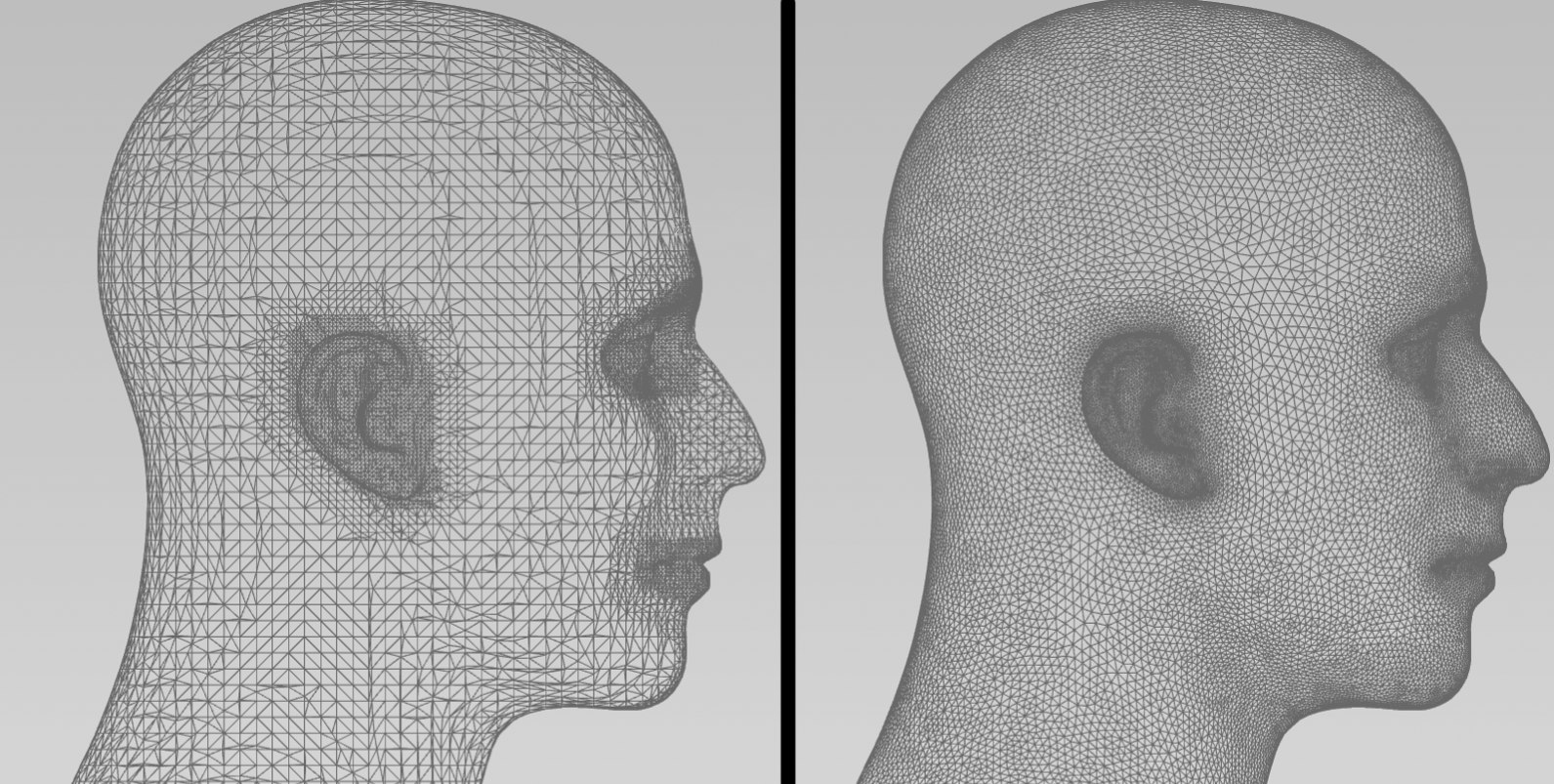
Кстати, можно заметить что оригинал был получен с помощью алгоритма Марширующих Кубов.
Ну и картинки поменьше, но уже из интернета:
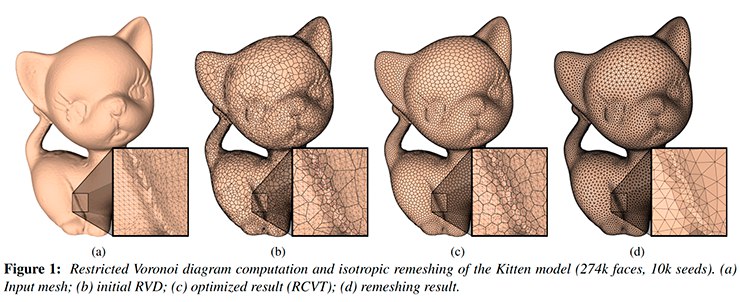
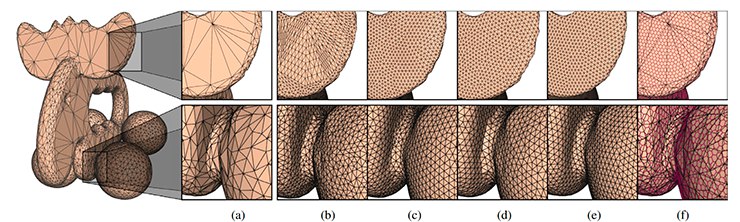
И… (куда ж без нее то) — статуя Давида:

Красота, да и только!
Завершить хотел бы на том, что использование алгоритма Ллойда, дело затратное. И для получения более быстрого результата, без особой потери в качестве были разработаны так называемые методы 'Минимизации Энергии'. Почитать можно в [2]
Полезные ссылки и литература
[0] Крутая статья на Хабрахабр-е о диаграммах Вороного
[1] Оригинал описания алгоритма, со всеми доказательствами
[2] Сравнение методов 'Минимизации Энергии'
[3] Небольшая статья о 'Разделяй и властвуй' алгоритме построения диаграммы Вороного
Автор: IvanKamynin