Всем привет!
Вы читаете третью часть статьи про создание VST-синтезатора на С#. В предыдущих частях был рассмотрен SDK и библиотеки для создания VST плагинов, рассмотрено программирование осциллятора и ADSR-огибающей для управления амплитудой сигнала.
В этой части я расскажу, как рассчитать и закодить фильтр частот, без которого не обходится ни один синтезатор. А без эквалайзера немыслима обработка звука.
Будет рассмотрен исходный код и применение эквалайзера из библиотеки NAudio (библиотека для работы со звуком под .NET).
Внимание — будет много матана — будем рассчитывать формулы для коэффициентов фильтра.
Исходный код написанного мною синтезатора доступен на GitHub'е.
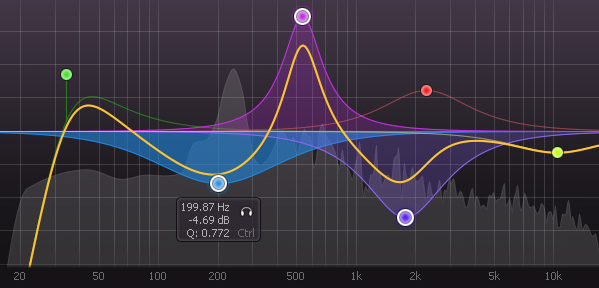
Скриншот VST плагина-эквалайзера Fab Filter Pro Q
Цикл статей
- Понимаем и пишем VSTi синтезатор на C# WPF
- ADSR-огибающая сигнала
- Частотный фильтр Баттервота
- Продолжение следует...
Оглавление
- Эквалайзер
- Фильтрация через преобразование Фурье
- Цифровые фильтры
- Почему фильтр Баттервота?
- Вывод формулы фильтра НЧ
- Вывод формулы фильтра ВЧ и полосового фильтра
- Программирование фильтра Баттервота по полученным формулам
- Полосовой эквалайзер в библиотеке NAudio
- Программы для рассчета фильтров
- Список литературы
Эквалайзер
Часто при обработке звука мы хотим изменить его характер/окраску/тембр. Сделать звук более басовым, убрать верхние частоты, или наоборот, сделать звук "прозрачным", оставив лишь середину и верха. Уверен, многие люди, не работавшие с обработкой звука, знают что такое эквалайзер — они есть акустических колонках, музыкальных центрах, магнитофонах, плеерах, и т.д. Эквалайзер — это набор фильтров, каждый из которых изменяет амплитуду сигнала в его выбранной полосе частот. На бытовых колонках это, обычно, 2-3 крутилки — низкие частоты, средние и верха, с фиксированными полосами частот.
В Winamp'овском эквалайзере уже есть 10 заранее определенных полос.
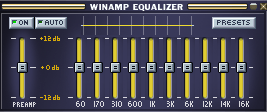
Скриншот эквалайзера в плеере Winamp
В мире обработки звука существует множество плагинов-эквалайзеров, на любой вкус и цвет. Плагин Fab Filter Pro Q (скриншот в начале статьи) — это графический эквалайзер, позволяющий создавать большое число полос и редактировать их параметры.
Каждая полоса в эквалайзере — это, по сути, фильтр частот. Фильтры частот изменяют тембральные/частотные характеристики сигнала. В электронике существуют много типов и классификаций фильтров, с соответствующими характеристиками и параметрами — смотрим википедию.
Мы рассмотрим и запрограммируем самые простые фильтры: НЧ, ВЧ и полосовой фильтры.
Фильтрация через преобразование Фурье
По идее, вам никто не мешает делать с сигналом дискретное преобразование Фурье, обработать частоты и затем сделать обратное преобразование.
Если не думать над реализацией ДПФ, то такой подход я бы назвал достаточно интуитивным и простым в программировании (опять же, если взять ДПФ из какой-нибудь либы и не кодить самому).
Минусы подхода — во-первых, ДПФ принимает на вход массив из семплов, размер которого является степенью двойки. Это значит, что выходной сигнал уже будет с задержкой. Во вторых, каждый 512-й семпл мы будем производить данный алгоритм: ДПФ, обработка частот сигнала, обратное ДФП. Это не малые вычисления. В-третьих, есть еще минусы и тонкости, которые знают адепты цифровой обработки сигналов.
Мы не будем рассматривать применение ДПФ, а заглянем в теорию цифровых фильтров; напишем фильтр, который обрабатывает значения семплов и имеет линейную вычислительную сложность в зависимости от длины входящего массива семплов.
Цифровые фильтры
Большую часть информации и вывод формул я взял из книги Digital Signal Processing: A Practical Approach — очень рекомендую, она есть в русской версии — Цифровая обработка сигналов. Практический подход, заинтересованные найдут PDF в сети.
Хочу сделать важное замечание. Тема построения и рассчитывания фильтра действительно очень сложна, содержит массу тонкостей и нюансов, требует знания и понимания теории. В этой статье я покажу, как рассчитать формулы фильтра Баттервота, чтобы у читателя возникло понимание, откуда выводятся эти формулы. Но почему именно такие исходные формулы, почему именно такие замены — можно понять лишь погрузившись в глубокую теорию цифровой обработки сигналов.
Когда я начинал гуглить код фильтров, я сразу находил множество непонятного математического кода, и хотелось хоть чуть-чуть понять, откуда берутся такие рассчетные формулы. Осциллятор, огибающая, дилей — понимание и программирование работы этих составляющих лично мне кажется интуитивным, но только не фильтров. Этой статьей я хочу пробудить интерес к цифровой обработке сигналов) Буду рад, если возникнет желание разобраться в этой теме более основательно.
Вам нужно знать (хотя бы немножко) такие термины как свертка, импульсная характеристика фильтра, передаточная функция фильтра.
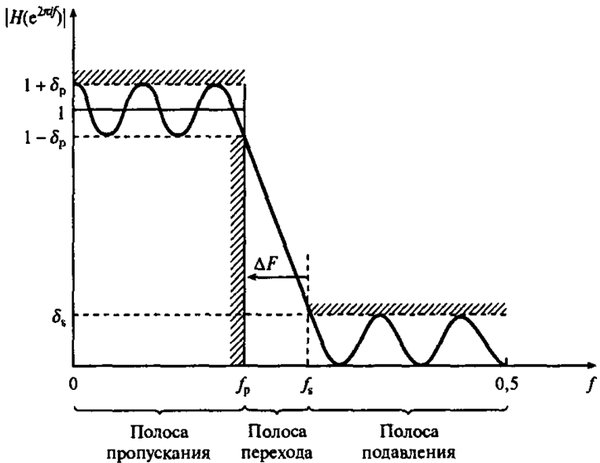
Аппроксимация АЧХ идеального фильтра (картинка из советского учебника, не нашел исходник)
Фильтр изменяет сигнал, "убирая" в нем выбранные частоты. Существующие фильтры не идеальны. Полоса пропускания — полоса частот, которую фильтр "не затрагивает" (на графике есть некоторая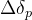 
изменения — особенность неидеального представленного фильтра). Полоса подавления — полоса нежелательных частот. В полосе перехода происходит спад частот. Естественно, фильтр ближе к "идеальному" тем, насколько меньше он искажает полосу пропускания, насколько сильно он подавляет частоты в полосе подавления и насколько узка полоса перехода. Есть разные "приближения" фильтров — фильтр Чебышёва, Баттервота, и так далее — их вы найдете в книжках и на просторах сети.
Почему фильтр Баттервота?
Все очень просто, АЧХ фильтра Баттерворта максимально гладкая на частотах полосы пропускания — имхо, важнее всего не испортить сигнал в полосе пропускания.
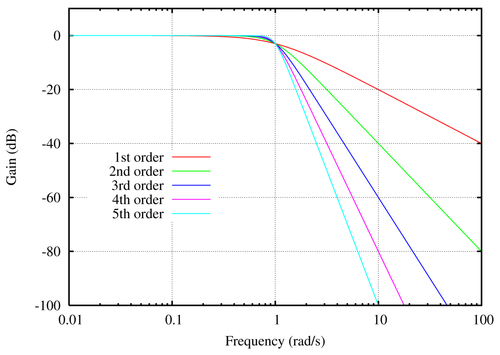
Логарифмическая АЧХ для фильтров Баттерворта нижних частот разных порядков (скриншот взят с Википедии)
Вывод формулы фильтра НЧ
Передаточная функция для фильтра Баттервота на s-плоскости записывается следующими формулами:
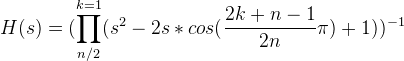при четных n и
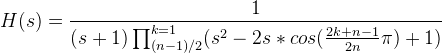при нечетных n
Здесь n — порядок фильтра: амплитуда на частоте среза w равна -3n dB, амплитудно-частотная характеристика затухает на −6n dB на октаву.
Чтобы получить сверточные коэффициенты, нужно получить передаточную функцию на z-плоскости в виде
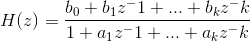
Найдем передаточную функцию для фильтра второго порядка (затухание на -6 dB на октаву), подставляем в формулу для H(s) n = 2:
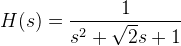
Тогда свертка для фильтра будет выглядеть так:
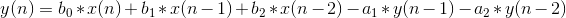
Пусть нам заданы частота среза w (на которой амплитуда сигнала будет -3 dB) и Fc — частота дискретизации (число семплов в секунду), в герцах.
В формуле нужно использовать денормированные частоты, т.е. произвести замену (в полосовом фильтре будут две частоты w1 и w2, определяющие полосу пропускания):
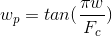
Если мы хотим рассчитывать НЧ-фильтр, то нужно сделать преобразование — произвести замену параметра s в передаточной функции:
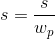
Для рассчета других типов фильтров (ВЧ, полосового, режекторного) нужно делать другие замены. Они рассмотрены в книге Цифровая обработка сигналов. Практический подход в части 8.8.2 и далее в статье.
Далее, для перехода в z-плоскость делаем замену:
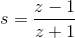
Для аналитических рассчетов я использовал пакет Mathematica.
Нужно получить числитель и знаменатель в виде полиномов от z. Приведем слагаемые знаменателя H(z) к общему знаменателю. Для этого найдем наибольший общий делитель (НОД, GCD) слагаемых знаменателя и поделим на него числитель и знаменатель исходной функции H(z).
Найдем коэффициенты при степенях у полученных полиномов, используя функцию CoefficientList:
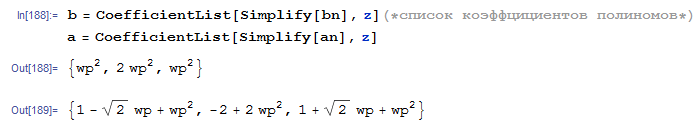
Если все делать честно, то, по условию, a0 должен быть равен 1 — поделим на a0 все коэффициенты (для кодинга будем использовать предыдущие формулы без деления):
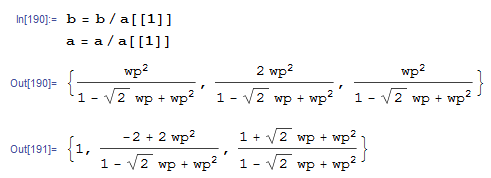
Вывод формулы фильтра ВЧ и полосового фильтра
Вывод формул для ВЧ-фильтра аналогичен НЧ-фильтру с другим преобразованием:
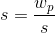
Для вывода формул полосового фильтра применяется преобразование:
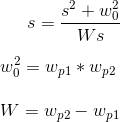
Если производить замену, то степень полиномов в числителе и знаменателе H(z) удвоится (в замене есть s^2), значит порядок фильтра увеличится вдвое. Поэтому изначально используем функцию H(s) для n = 1:
Программирование фильтра Баттервота по полученным формулам
Фильтр будет иметь 2 параметра: тип фильтра (НЧ, ВЧ, полосовой) и частота среза w. Для полосового фильтра будем рассматривать частоту среза как частоту посередине полосы пропускания. Полосу пропускания же определим как отрезок частот [w — w/4, w + w/4] (можно придумать здесь более сложный и логичный здесь логарифмический закон, на ваше усмотрение).
Пусть мы определили коэффициенты b0, b1, b2, a1 и a2 (a0 по условию равен 1) по рассчитанным формулам. Алгоритм работы фильтра сводится к свертке, которая делается последовательно для каждого семпла:
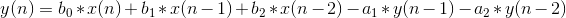
y(n) — это новое значение семпла, которое нужно рассчитать. x(n) — текущее значение семпла, соответственно y(n-1) и y(n-2) — предыдущие 2 рассчитанных семпла, а x(n-1) и x(n-2) — предыдущие входные значения семплов.
Нужно организовать запоминание предыдущих семплом.
Не будем мудрить с циклическими буферами, сделаем просто и понятно: два массива из трех элементов. Каждый раз будем "проталкивать" новые значения в этот массив, последовательно копируя более старые значения семплов.
Получаем простой класс:
class BiquadConvolutionTable
{
public double B0, B1, B2, A1, A2;
private readonly double[] _x = new double[3];
private readonly double[] _y = new double[3];
public double Process(double s)
{
// "сдвигаем" предыдущие семплы
_x[2] = _x[1];
_x[1] = _x[0];
_x[0] = s;
_y[2] = _y[1];
_y[1] = _y[0];
// свертка
_y[0] = B0 * _x[0] + B1 * _x[1] + B2 * _x[2] - A1 * _y[1] - A2 * _y[2];
return _y[0];
}
}Напишем каркасный класс для фильтра (смотри архитектуру синтезатора в первой статье).
Класс BiquadConvolutionTable работает с одним сигналом, т.е. с одним каналом — моно. Поэтому нам нужны две BiquadConvolutionTable — для левого и правого каналов.
Чтобы корректно применить фильтр, нужно последовательно, для всех семплов входящей последовательности применить функцию BiquadConvolutionTable.Process и заполнить результирующий массив семплов.
Рассчетом коэффициентов для BiquadConvolutionTable будет заниматься функция CalculateCoefficients.
public enum EFilterPass
{
None,
LowPass,
HiPass,
BandPass
}
public class ButterworthFilter : SyntageAudioProcessorComponentWithParameters<AudioProcessor>, IProcessor
{
private readonly BiquadConvolutionTable _tablel;
private readonly BiquadConvolutionTable _tabler;
public EnumParameter<EFilterPass> FilterType { get; private set; }
public FrequencyParameter CutoffFrequency { get; private set; }
public ButterworthFilter(AudioProcessor audioProcessor) : base(audioProcessor)
{
_tablel = new BiquadConvolutionTable();
_tabler = new BiquadConvolutionTable();
}
public override IEnumerable<Parameter> CreateParameters(string parameterPrefix)
{
FilterType = new EnumParameter<EFilterPass>(parameterPrefix + "Pass", "Filter Type", "Filter", false);
CutoffFrequency = new FrequencyParameter(parameterPrefix + "Cutoff", "Filter Cutoff Frequency", "Cutoff");
return new List<Parameter> {FilterType, CutoffFrequency};
}
public void Process(IAudioStream stream)
{
if (FilterType.Value == EFilterPass.None)
return;
var count = Processor.CurrentStreamLenght;
var lc = stream.Channels[0];
var rc = stream.Channels[1];
for (int i = 0; i < count; ++i)
{
var cutoff = CutoffFrequency.Value;
CalculateCoefficients(cutoff);
var ls = _tablel.Process(lc.Samples[i]);
lc.Samples[i] = ls;
var rs = _tabler.Process(rc.Samples[i]);
rc.Samples[i] = rs;
}
}
private void CalculateCoefficients(double cutoff)
{
...
}
}Функция CalculateCoefficients вызывается каждый раз в цикле — зачем? В следующей статье я расскажу про модуляцию (изменение во времени) параметров, и поэтому, частота среза может меняться, а значит, нужно перерассчитывать коэффициенты. Конечно, по-трушному, нужно подписаться на изменение частоты среза и уже в обработчике рассчитывать коэффициенты. Но в этих статьях я оптимизами заниматься не буду, цель — закодить фильтр.
Осталось закодить функцию CalculateCoefficients по рассчитаным формулам для коэффициентов.
Вспомним, что нужно использовать денормированные частоты, т.е. произвести замену:
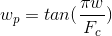
Списываем все формулы для коэффициентов b0, b1, b2, a0, a1, a2. После рассчетов нужно поделить все коэффициенты на a0, чтобы a0 стало равно 1.
private double TransformFrequency(double w)
{
return Math.Tan(Math.PI * w / Processor.SampleRate);
}
private void CalculateCoefficients(double cutoff)
{
double b0, b1, b2, a0, a1, a2;
switch (FilterType.Value)
{
case EFilterPass.LowPass:
{
var w = TransformFrequency(cutoff);
a0 = 1 + Math.Sqrt(2) * w + w * w;
a1 = -2 + 2 * w * w;
a2 = 1 - Math.Sqrt(2) * w + w * w;
b0 = w * w;
b1 = 2 * w * w;
b2 = w * w;
}
break;
case EFilterPass.HiPass:
{
var w = TransformFrequency(cutoff);
a0 = 1 + Math.Sqrt(2) * w + w * w;
a1 = -2 + 2 * w * w;
a2 = 1 - Math.Sqrt(2) * w + w * w;
b0 = 1;
b1 = -2;
b2 = 1;
}
break;
case EFilterPass.BandPass:
{
var w = cutoff;
var d = w / 4;
// определим полосу фильтра как [w * 3 / 4, w * 5 / 4]
var w1 = Math.Max(w - d, CutoffFrequency.Min);
var w2 = Math.Min(w + d, CutoffFrequency.Max);
w1 = TransformFrequency(w1);
w2 = TransformFrequency(w2);
var w0Sqr = w2 * w1; // w0^2
var wd = w2 - w1; // W
a0 = -1 - wd - w0Sqr;
a1 = 2 - 2 * w0Sqr;
a2 = -1 + wd - w0Sqr;
b0 = -wd;
b1 = 0;
b2 = wd;
}
break;
default:
throw new ArgumentOutOfRangeException();
}
_tablel.B0 = _tabler.B0 = b0 / a0;
_tablel.B1 = _tabler.B1 = b1 / a0;
_tablel.B2 = _tabler.B2 = b2 / a0;
_tablel.A1 = _tabler.A1 = a1 / a0;
_tablel.A2 = _tabler.A2 = a2 / a0;
}public enum EFilterPass
{
None,
LowPass,
HiPass,
BandPass
}
public class ButterworthFilter : SyntageAudioProcessorComponentWithParameters<AudioProcessor>, IProcessor
{
private class BiquadConvolutionTable
{
public double B0, B1, B2, A1, A2;
private readonly double[] _x = new double[3];
private readonly double[] _y = new double[3];
public double Process(double s)
{
// "сдвигаем" предыдущие семплы
_x[2] = _x[1];
_x[1] = _x[0];
_x[0] = s;
_y[2] = _y[1];
_y[1] = _y[0];
// свертка
_y[0] = B0 * _x[0] + B1 * _x[1] + B2 * _x[2] - A1 * _y[1] - A2 * _y[2];
return _y[0];
}
}
private readonly BiquadConvolutionTable _tablel;
private readonly BiquadConvolutionTable _tabler;
public EnumParameter<EFilterPass> FilterType { get; private set; }
public FrequencyParameter CutoffFrequency { get; private set; }
public ButterworthFilter(AudioProcessor audioProcessor) : base(audioProcessor)
{
_tablel = new BiquadConvolutionTable();
_tabler = new BiquadConvolutionTable();
}
public override IEnumerable<Parameter> CreateParameters(string parameterPrefix)
{
FilterType = new EnumParameter<EFilterPass>(parameterPrefix + "Pass", "Filter Type", "Filter", false);
CutoffFrequency = new FrequencyParameter(parameterPrefix + "Cutoff", "Filter Cutoff Frequency", "Cutoff");
return new List<Parameter> {FilterType, CutoffFrequency};
}
public void Process(IAudioStream stream)
{
if (FilterType.Value == EFilterPass.None)
return;
var count = Processor.CurrentStreamLenght;
var lc = stream.Channels[0];
var rc = stream.Channels[1];
for (int i = 0; i < count; ++i)
{
var cutoff = CutoffFrequency.Value;
CalculateCoefficients(cutoff);
var ls = _tablel.Process(lc.Samples[i]);
lc.Samples[i] = ls;
var rs = _tabler.Process(rc.Samples[i]);
rc.Samples[i] = rs;
}
}
private double TransformFrequency(double w)
{
return Math.Tan(Math.PI * w / Processor.SampleRate);
}
private void CalculateCoefficients(double cutoff)
{
double b0, b1, b2, a0, a1, a2;
switch (FilterType.Value)
{
case EFilterPass.LowPass:
{
var w = TransformFrequency(cutoff);
a0 = 1 + Math.Sqrt(2) * w + w * w;
a1 = -2 + 2 * w * w;
a2 = 1 - Math.Sqrt(2) * w + w * w;
b0 = w * w;
b1 = 2 * w * w;
b2 = w * w;
}
break;
case EFilterPass.HiPass:
{
var w = TransformFrequency(cutoff);
a0 = 1 + Math.Sqrt(2) * w + w * w;
a1 = -2 + 2 * w * w;
a2 = 1 - Math.Sqrt(2) * w + w * w;
b0 = 1;
b1 = -2;
b2 = 1;
}
break;
case EFilterPass.BandPass:
{
var w = cutoff;
var d = w / 4;
// определим полосу фильтра как [w * 3 / 4, w * 5 / 4]
var w1 = Math.Max(w - d, CutoffFrequency.Min);
var w2 = Math.Min(w + d, CutoffFrequency.Max);
w1 = TransformFrequency(w1);
w2 = TransformFrequency(w2);
var w0Sqr = w2 * w1; // w0^2
var wd = w2 - w1; // W
a0 = -1 - wd - w0Sqr;
a1 = 2 - 2 * w0Sqr;
a2 = -1 + wd - w0Sqr;
b0 = -wd;
b1 = 0;
b2 = wd;
}
break;
default:
throw new ArgumentOutOfRangeException();
}
_tablel.B0 = _tabler.B0 = b0 / a0;
_tablel.B1 = _tabler.B1 = b1 / a0;
_tablel.B2 = _tabler.B2 = b2 / a0;
_tablel.A1 = _tabler.A1 = a1 / a0;
_tablel.A2 = _tabler.A2 = a2 / a0;
}
}Полосовой эквалайзер в библиотеке NAudio
Для работы с звуком, звуковыми файлами различных форматов на .NET есть хорошая библиотека NAudio.
Она содержит пространство имен NAudio.Dsp с функционалом для фильтрации, свертки, гейта, огибающей, БПФ и других интересных штук.
Рассмотрим класс Equalizer (из примеров, пространство имен NAudioWpfDemo.EqualizationDemo), позволяющий производить эквализацию сигнала. Класс реализует ISampleProvider, который в функции Read(float[] buffer, int offset, int count) обрабатывает (изменяет) массив семплов buffer.
Конструктор принимает массив структуры EqualizerBand, которые описывают "полосы" эквалайзера:
class EqualizerBand
{
public float Frequency { get; set; }
public float Gain { get; set; }
public float Bandwidth { get; set; }
}Здесь Frequency — центральная частота полосы с параметром Q (Bandwidth, добротность фильтра), c усилением Gain dB.
Если заглянуть в реализацию, то каждой полосе EqualizerBand соответствует класс BiQuadFilter который используется как полосовой (Peaking) фильтр. Все фильтры изменяют сигнал используются последовательно.
Класс EqualizerBand является реализацией фильтра Баттервота, с большим выборов типов фильтров и параметрами. Если посмотреть реализацию, можно увидеть схожие формулы и коэффициенты.
Пример использования класса Equalizer вы найдете в проекте NAudioWpfDemo в классе EqualizationDemoViewModel.
Программы для рассчета фильтров
Прародителем цифровых фильтров были фильтры аналоговые. Теория для аналоговых схем и аналоговой обработке сигналов в дальнейшем переросла в теорию цифровой обработки сигналов.
Для рассмотренного фильтра Баттервота и рассчитанных формул для коэффициентов можно собрать аналоговую схему.
Есть много программ для рассчета и построения схем, параметров элементов для них, сверточных коэффициентов различных фильтров.
Можете погуглить по "filter calculation software".
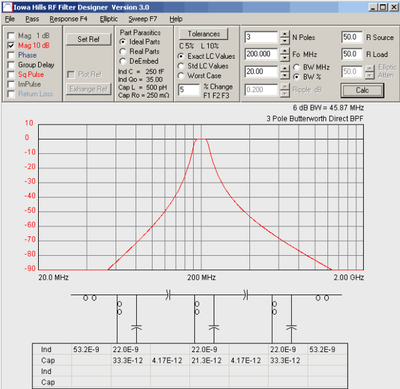
Iowa Hills Software RF Filter Designer
В следующей статье я расскажу про эффект delay, distortion и модуляцию параметров.
Всем добра!
Удачи в программировании!
Список литературы
Не забывайте смотреть списки статей и книг в предыдущих статьях.
- Digital Signal Processing: A Practical Approach. Русская версия — Цифровая обработка сигналов. Практический подход.
- Хабр-статья "Простыми словами о преобразовании Фурье"
- Фильтр Баттерворта на вики
- Github-репозитарий с кодом для рассчета фильтров Баттервота
- DISCRETE SIGNALS AND SYSTEMS, Chapter 7. FIR and IIR Filters
- How does a low-pass filter programmatically work? (dsp.stackexchange.com/)
- Designing Digital Butterworth and Chebyshev Filters
- Audio EQ Cookbook
- Iowa Hills Software — Digital and Analog Filters
Автор: lis355
