Много чего предстоит сделать, прежде чем мы дойдем до вот этой картинки:

Опуская росказни о том, как именно я пришел к мысли построить гексапода (это были тонны видео на ютубе), перейду сразу к процессу выбора деталек. Это был январь 2012-го. Я сразу знал, чего я хочу от своего робота, а чего — нет. Я хотел:
— каждая нога должна иметь 3 степени свободы — 3dof (3 dimensions of freedom). Потому что более простой вариант 2dof — не дает такого ощущения насекомого, а 4dof — излишне, 3dof и так позволяет свободно перемещать кончик ноги в 3д пространстве;
— 6 ног; снова-таки, это уже не 4 (тогда робот неуклюже скачет), но и еще и не 8, как у пауков и уже чрезмерно;
— небольшой;
— дешевый;
— минимум плат и соединений;
Пост большой.
Первой конечно нужно было выбирать motherboard для крохи. Много как хорошего так и плохого успел почитать к тому времени об Arduino. Но именно на него и смотрел, как на основной вариант. Паять контроллеры самому — времени не было, а брать более продвинутые платы с ARM cpu, например — дорого, да и разбираться, как их программить, как работать с ШИМ выводами и т.п. А ардуина: IDE запустил, код напедалил, upload нажал — и привет, оно тебе уже моргает. Красота! ;)
Сначала я начал смотреть на arduino mega и клонов, т.к. кол-во ШИМ выходов, которыми можно рулить сервами у них было предостаточно. Напомню, что для 3dof гексапода нужно 3*6 = 18 сервов, и раздельных каналов управления ими. Но потом я нашел настоящий Яззь среди arduino mega, это плата от Dagu, звать которую Red Back Spider Controller. Вот она на ebay.
Она предлагает все свои выходы в виде готовых 3-х штырьков (земля, питание, сигнал), и разввязку по питанию. Питание самого контроллера стабилизировано, а на разъемы двиглов идет как есть. Это позволяет просто подать на клемму питания 7-30 вольт достаточной мощности (питальника от eee pc 901 на 12В и 3А — оказалось достаточно для жужжания всеми 18 сервами) и не морочить голову с раздельным питанием логики и двиглов. Также это позволит в будущем легко посадить все это чудище на пачку Li-Po аккумуляторов на 7.4 вольт. И при всем этом, с программной точки зрения — это обычная ардуино мега, совместимая с софтом и либами, да и железом (кроме шилдов, устанавливающихся прямо на оригинальную mega — они не покатят). Правда цена еще выше чем даже оригинальная мега, но все остальные плюсы перевесили это.
Далее сервоприводы. На ebay по запросу micro servo их много разных. Я взял самые мощные из самых маленьких и дешевых — с моментом 9g, пластмассовыми редукторами. Если брать лоты где их пачками шлют — выходит дешевле. Я брал 3 пачки по 6 кажется, и вышло меньше $2 штука. Забегая вперед, скажу, что жалею что не потратил больше и не взял сервы с металлическими шестернями и шариковыми подшипниками. У этих пластмассовых оказались довольно заметные люфты, и характерный хруст при чрезмерном усилии когда шестерни проскакивают. Из-за люфтов — кинематику довольно тяжело настроить точно (да это вообще самое тяжелое оказалось).
Вот собственно и все что я заказал, с доставкой это вышло примерно $100. Батарейки и передатчикиприемники для контроля и радиоуправляемости — оставил на потом. Потому что радиоуправляемая машинка у меня есть и не интересна, а что меня действительно интересовало — это ноги! Видео плавно ходящих гексаподов на ютубе — завораживало, я смотрел его, пересматривал, и каждый раз слезы котились по щекам, и я сдавлено хрипел «хочу!». Хочу не заказать такую готовую штуку, а хочу сделать самому что-нибудь такое!
Пока ждал заказа, читал, как же просвященные люди оживляют свои творения. Конечно сразу же всплыла инверсная кинематика (перевод). Если сказать просто и сразу про шарнитные «конечности», то прямая кинематика — это когда на вход подаются углы шарниров, а на выходе мы имеем модель конечности в пространстве, и координаты крайней точки конечности. Обратная же кинематика — очевидно работает наоборот — на вход поступают координаты крайней точки конечности, куда нам надо дотянуться, а на выходе мы получаем углы, на которые нужно повернуть шарниры, чтобы это осуществить. Сервоприводы как раз получают на вход угловое положение, в которое им нужно повернуться (по одному сигнальному проводу, закодированное ШИМ / PWM).
Начал писать. Начал с того, о чем читал: продумывать реализацию ИК по методу, описанному там. Но быстро пришло ощущение, что для моего случая он чрезмерно сложен. Причем как громоздок в реализации, так и вычислительно очень сложен — расчет идет итеративно. А у меня 6 ног, для каждой из которых нужно считать ИК, и всего 16Мгц не самой шустрой архитектуры AVR. Но и всего 3 степени свободы. И несложно догадаться, что до произвольной точки в «области дотягивания» можно дотянуться только одним способом. Решение уже созрело в голове.
Но тут пришел февраль и посылки — одна из китая, другая из UK. Первым делом я конечно просто поигрался с платой ардуино — поморгал светодиодом и попиликал в подключеный туда динамик. Потом занялся реализацией собственно ИК, уже в железе. Для чего соорудил прототип ноги из подручных материалов (довольно мягкая пластмасска, которую легко резать ножницами, шурупы и насадки — все из комплектов сервоприводов). Эту ногу терминатора закрепил прямо на плату ардуины. Можно рассмотреть, как бюджетно выполнены сочленения.


Полюбовался на это дело, и помечтал, что если я на основе этого робота в будущем спаяю терминатора, который объявит войну человечеству, то потом Джон Коннор со Шварцнеггером вернутся ко мне сюда в прошлое, и отберут этот прототип и расплавят его в Ородруине. Но никто не вернулся, ничего не отобрал, и я спокойно продолжил.
Оказалось, что ИК совсем не нужно бояться, в моем случае все свелось к банальной геометрии-тригонометрии. Чтобы проще было обращаться к суставам, обратился к википедии и почитал про насекомых. У них есть специальные названия для элементов конечности:
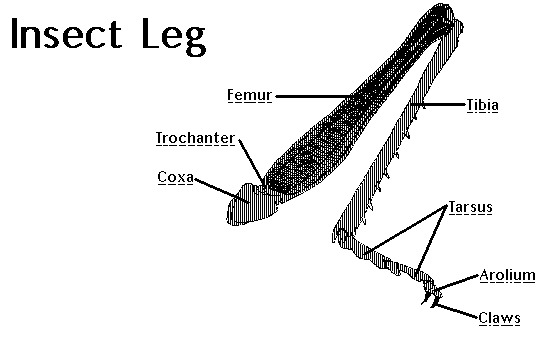
На русском тоже есть свои и очень интересные названия для этого, но «тазик», «вертлуг», «голень» и т.п., находясь в коде, не давали бы мне заснуть. Потому я 3-х конечностям и соответствующим сервам оставил названия Coxa, Femur, Tibia. Из прототипа ноги выше видно, что у меня для coxa даже нет отдельной детали. Это просто два серва, скрепленных резинками. Femur — реализован полоской пластика, к которой с обоих сторон крепятся рычаги сервов. Таким образом, последний оставшийся серводвижок — является началом tibia, для удлинения которой к нему прикручен еще кусок пластика.
Запустил редактор, не мудствуя создал файл Leg.h, И в нем класс Leg. Ну и кучу вспомогательной мути .) Пускай в пространстве есть точка A(ax, ay, az), к которой нужно дотянуться. Тогда вид сверху выглядит так:
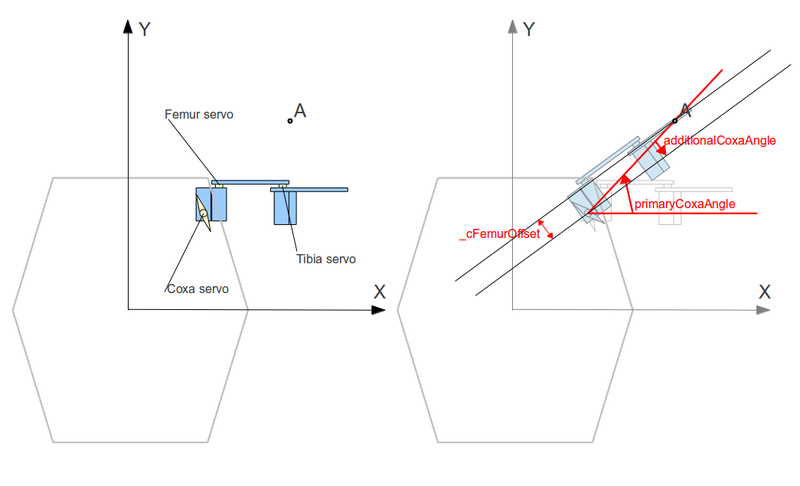
На рисунке я сразу показал и способ вычисления первого угла — это угол поворота серва, управляющего Coxa, вращающего всю конечность в горизонтальной плоскости. На схеме красным сразу обозначены переменные, используемые в коде (далеко не все). Не очень математично, зато удобно. Видно, что интересующий нас угол находится элементарно. Сначала primaryCoxaAngle — находится просто углом (0;A) к оси X (что эквивалентно углу точки A в полярных координатах). Но на схеме видно, что при этом сама нога — не распаложена под этим углом. Причина в том, что ось вращения coxa не находится на «линии ноги» — не знаю как это правильно сказать. Не находится в плоскости, в которой вращаются остальные 2 сустава и находится кончик ноги, вот. Это можно легко компенсировать, посчитав additionalCoxaAngle (как его считать — даже не утруждаюсь останавливаться, ну ведь все же были в школе, правда?).
Итого, у нас есть первый кусочек кода, это внутренности метода reach(Point& dest):
float hDist = sqrt( sqr(dest.x - _cStart.x) + sqr(dest.y - _cStart.y) );
float additionalCoxaAngle = hDist == 0.0 ? DONT_MOVE
: asin( _cFemurOffset / hDist );
float primaryCoxaAngle = polarAngle(dest.x - _cStart.x, dest.y - _cStart.y, _thirdQuarterFix);
float cAngle = hDist == 0.0 ? DONT_MOVE
: primaryCoxaAngle - additionalCoxaAngle - _cStartAngle;
Здесь dest — это точка, куда нажо тянуться, _cStart — координаты точки крепления (и центра вращения) coxa, в hDist считаем расстояние от _cStart до dest в горизонтальной плоскости. DONT_MOVE — это просто флаг, означающий что coxa не нужно никуда вращать, а оставить в текущем положении (т.к. dest — где-то прямо на оси вращения coxa — редко, но бывает). Вот cAngle — это уже тот угол, на который нужно будет отклониться сервоприводу от его начального угла (который находится в середине его рабочего диапазона). Видно что также юзается _cStartAngle — это угол в пространстве, на который повернут серво по деволту, при монтаже. Про _thirdQuarterFix расскажу позже, если не забуду.
Дальше все становится еще проще. Нам просто нужно взглянуть на упомянутую выше плоскость «линии ноги»:
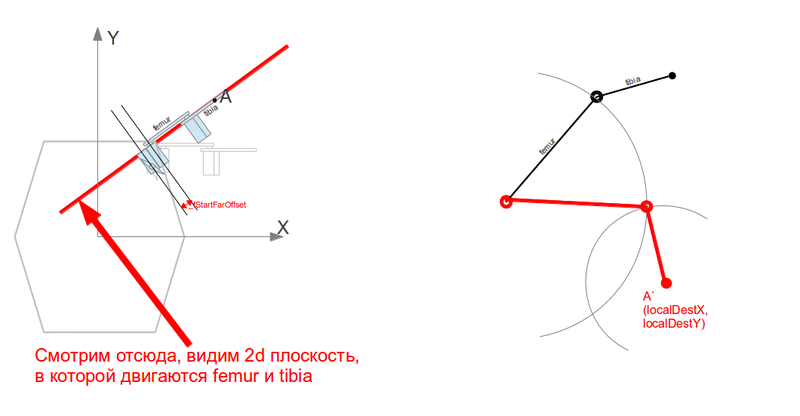
При этом, задача внезапно сведется к поиску точки пересечения 2-х окружностей. Одна — в точке, откуда «растет» наша femur, вторая — точка, куда нам надо дотянуться (с уже локальным 2d координатами). Радиусы окружностей — длины femur и tibia соответственно. Если окружности пересекаются — то в одной из 2х точек можно расположить сустав. Мы всегда выбираем верхнюю, чтобы «колени» у чудища были выгнуты вверх, а не вниз. Если не пересекаются — то мы не дотянемся до целевой точки. Еще немного кода, переход в плоскость производится элементарно, только пара подводных камней еще учтена и задокументирована в коментарии, чтобы я не ломал голову потом, разбирая код. Для простоты, в этой локальной координатной «плоскости ноги» я выбрал началом координат точку, откуда растет femur:
// Moving to local Coxa-Femur-target coordinate system
// Note the case when hDist <= _cFemurOffset. This is for the blind zone.
// We never can't reach the point that is nearer to the _cStart then
// femur offset (_fStartFarOffset)
float localDestX = hDist <= _cFemurOffset
? - _fStartFarOffset
: sqrt(sqr(hDist) - sqr(_cFemurOffset)) - _fStartFarOffset;
float localDestY = dest.z - _fStartZOffset;
// Check reachability
float localDistSqr = sqr(localDestX) + sqr(localDestY);
if (localDistSqr > sqr(_fLength + _tLenght))
{
log("Can't reach!");
return false;
}
Теперь localDestX и localDestY — это координаты целевой точки. Все что осталось — найти точку пересечения окружностей с центрами в (0,0) и (localDestX, localDestY), и радиусами _fLength и _tLength (соответственно длина femur и длина tibia). С этим тоже школьник справится, но тут я допускал довольно много ошибок, потому для проверки себя и вообще чтобы любой мог проверить, что это за стремные формулы, оставил ссылки на источники, где ясно и понятно разжована эта элементарная геометрическая задача:
// Find joint as circle intersect ( equations from http://e-maxx.ru/algo/circles_intersection & http://e-maxx.ru/algo/circle_line_intersection )
float A = -2 * localDestX;
float B = -2 * localDestY;
float C = sqr(localDestX) + sqr(localDestY) + sqr(_fLength) - sqr(_tLenght);
float X0 = -A * C / (sqr(A) + sqr(B));
float Y0 = -B * C / (sqr(A) + sqr(B));
float D = sqrt( sqr(_fLength) - (sqr(C) / (sqr(A) + sqr(B))) );
float mult = sqrt ( sqr(D) / (sqr(A) + sqr(B)));
float ax, ay, bx, by;
ax = X0 + B * mult;
bx = X0 - B * mult;
ay = Y0 - A * mult;
by = Y0 + A * mult;
// Select solution on top as joint
float jointLocalX = (ax > bx) ? ax : bx;
float jointLocalY = (ax > bx) ? ay : by;
Все, осталось еще чуть-чуть — по полученным координатам вычислить собственно углы для femur и tibia сервов:
float primaryFemurAngle = polarAngle(jointLocalX, jointLocalY, false);
float fAngle = primaryFemurAngle - _fStartAngle;
float primaryTibiaAngle = polarAngle(localDestX - jointLocalX, localDestY - jointLocalY, false);
float tAngle = (primaryTibiaAngle - fAngle) - _tStartAngle;
Опять элементарщина — угловые координаты и всё. Я надеюсь, именование переменных уже должно быть понятным, к примеру, _fStartAngle — это femur start angle, угол на который femur направлен по дефолту. И последняя строчка метода reach() (он сказал поехали, и махнул рукой):
move(cAngle, fAngle, tAngle);
Метод move уже непосредственно отдает команды сервам. На самом деле, в нем еще потом пришлось добавить всякие штуки для защиты от нехороших углов (на которые серво повернуться не может, но будет пытаться), а также для других ног, которые заркально расположены и/или направлены в другие стороны. Но пока же мы работаем с одной только лапой.
Эти куски — это уже финальный код, который далек от совершенства, и наверняка его можно значительно улучшить. Но он работает! Ни разу не выйдя за школьный курс геометрии-тригонометрии, мы реализовали полнофункционалную инверсную кинематику для 3dof ноги! Да еще и получаем решение сразу, за одну итерацию. Чтобы это все работало, ногу нужно было тщательно измерить, и сконфигурировать класс полученными данными. в том числе угловыми, которые сложнее всего измерять на готовом изделии. Может если проектировать в автокаде и наделать красивых рендеров — было бы легче с измерением углов, но у меня не было ни времени, ни желания заниматься этим пафосом.
Февраль только начался, а видео с ногой было уже готово. Для проверки ИК, я заставлял ногу описывать всякие фигуры в пространстве (для этого нужно было последовательно вызывать reach, обходя точки на прямоугольнике, или окружности, код скучен и уныл, потому не привожу (а закончив эксперименты с обведением примитивов, я его вообще выпилил)):
Дальше нужно было заканчивать играться с этой поделкой, на одной ноге далеко не упрыгаешь (хотя такой робот вышел бы действительно интересным). Но мне нужен гексапод. Отправился на ближайшую барахолку искать оргстекло. Нашел 2 отличных куска — один 3 мм толщиной (как раз для туловища, подумал я), другой 2 мм и синий (отличные конечности, в тон сервоприводам). Еще через пару недель я выкроил вечер, чтобы что-нибудь сделать из этого. Сделал наброски на бумаге. примерил — вроде все ок, дальше дело за ножовкой.









И вот оно, чудище заморское, шестилапое. Когда я тестил одну ногу, я питал это дело каким-то левым питальником от внешнего винта. Хватало. Но питать 6 ног от него было уже страшновато. Потому я на некоторое время повесил руки, думая что мне нужно еще раздобыть подходящий питальник. Но оказалось все гораздо проще, я выше уже упоминал — подошел питальник от eee pc 901. Ну и отлично.
Отладить работу 6-ти ног оказалось еще сложнее, чем написать движок одной ноги. Половина ног была зеркально отражена относительно другой. Кроме того направлены все в разные стороны. Вобщем конфигурировал и настраивал я все очень долго, и это меня не очень вдохновляло, т.к. средств удобной отладки не было, максимум на что я мог расчитывать — вывод лога в Serial. И тот нормально работал из основного *.ino файла, а из подключенного Leg.h — уже не виделся нужный объект. Наворотил костылей для лога (facepalm). Со временем отрефакторю. А тут еще и весна пришла, велосезон был открыт в полную силу, и я забросил своего шестилапого питомца в шкаф. Так прошло все лето и теплая часть осени.
Но пошли дожди, стало холодно, и гексапод был извлечен. Ноги его были отлажены, в том числе был введен тот самый _thirdQuarterFix для функции расчета polarAngle. Проблема была в том, что 2 ноги (левая средняя и левая задняя) двигались так, что большую часть времени находились в III четверти:
А polarAngle у меня была наивная — она возвращала углы от -пи до пи, относительно оси X. И, если иногда одной из этих 2-х ног нужно было повернуться во II-ю четверть, то значение polarAngle прыгало от -пи до пи, что собственно негативно влияло на дальнейший расчет. Пофиксил костылем — для этих 2-х ног polarAngle считается «иначе». Стыдно, стыдно мне за код, но весь проект — это proof of concept, единственная цель которого — просто понять, могу я собрать реалистично двигающегося гексапода или нет. Потому код должен работать, и прямо сейчас. А уж потом рефакторинг — перерефакторинг.
Справившись с 3-й четвертью, начал педалить паттерны шага. Для этого ввел в класс Leg точку default, т.е. в которой нога находится, когда робот стоит смирно и ровно. Эту точку можно тюнинговать, главное чтобы все ноги были на одной z координате (чтобы при этом ноги реально физически находились на одной плоскости, у Leg есть еще самая низкоуровневая tuneRestAngles()). А в пределах одной Z координаты, их можно двигать почти как угодно. Почти — потому что диапазон движения не бесконечен, и чтобы при шаге не выходить за рамки этого диапазода — default положение ног старался разместить где-то поближе к центру этого диапазона.
Код тут в тексте уже не привожу, он слишком элементарен, и я в конце приведу ссылки на полную версию всех сорцов — заодно научусь пользоваться github.
Последовательность шага выбрал простую — 3 ноги на земле, 3 — в воздухе переставляются. Таким образом, координаты ног относительно их default положения — можно разделить на 2 группы. Для этих двух групп я и проворачивал шаг в цикле (см функцию walk() в Buggy.ino). А в итоге, каждая нога вычисляла себе свою индивидуальную координату, исходя из своей default координаты.
И он пошел! Но пока только вперед. На ноги надел ему резинки, чтобы не так скользил на линолеуме. И бросился снимать это на видео, чтобы показать друзьям.
До а-пода, конечно, далеко. Но я же не закончил еще .) Попедалил еще вечер — и добавил возможность двигаться в любом направлении (но не поворачивая корпус .)). Плюс для сглаживания между движениями добавил функцию (smoothTo()), которая аккуратно перемещает ноги (поднимая вверх, опять в 2-х группах, одна из которых всегда внизу, тварь на ней стоит, пока другая поднимается и перемещается) в новое положение. Это нужно чтобы тварь не дергала резко ногами, сменяя направление движения (этой фичи ох как не хватает многим игровым персонажам прошлых лет). И он резво забегал в любом направлении — вбок, по диагонали:
Оба грандиозных файла сорцов можно смотреть тут. Даю ссылку на конкретную ревизию, на момент написания этого текста. Так как в дальнейшем все может стать совсем иначе.
Результаты, которые пока можно выделить:
— склепать самому гексапода — дело выполнимое;
— написать ему кинематику самому с нуля — тоже вполне под силу любому (разработчику);
— бюджет может быть минимальным, единственное, на что действительно необходимо тратиться — это сервоприводы; а так, если есть паяльник, то можно любым микроконтроллером обойтись; чем удобнее, тем дороже, впрочем;
— на сервах лучше не экономить, но и самые дешевые — работают;
— такого удовольствия от программирования я не испытывал с 9-ти лет, когда впервые увидел на компьютерном кружке zx spectrum и научился писать первые программки для него; это так кайфово, когда твой код не просто где-то работает и чего-то там кому-то показывает, а бегает прямо перед тобой и пугает кошку.
Впереди более продвинутые алгоритмы для плавного перемещения тела, ну и беспроводное управление и батареи, конечно же.
Автор: poconoco






