10 сентября 2012 года завершился чемпионат по программированию Russian Code Cup 2012. Подробный рассказ о том, как все происходило, публиковался ранее, а сегодня мы разберем задачи, которые были предложены финалистам. Их было всего шесть, и каждая из них — отдельная интересная история:
10 сентября 2012 года завершился чемпионат по программированию Russian Code Cup 2012. Подробный рассказ о том, как все происходило, публиковался ранее, а сегодня мы разберем задачи, которые были предложены финалистам. Их было всего шесть, и каждая из них — отдельная интересная история:
- про злых птиц, шастающих по ветке,
- про жителей планеты Трисол — трисолианцев — с их хитрой системой ведения историй жизни,
- про сказочный город Альдерсберг, где ожидают решения наших финалистов (горожанам нужно расставить свои магические артефакты, чтобы выжить при осаде врагов),
- про нелегкую жизнь двухъядерного процессора,
- а также про машину, перемешивающую колоду карт
- и про нахождение протяженности гоночной трассы.
На решение этих задач выделялось три часа. Единственным решившим пять задач из шести оказался победитель Russian Code Cup 2012 Владислав Епифанов. Чуть менее половины финалистов решили по четыре задачи. Первые три задачи сделали почти все. Задачу про колоду карт правильно решил только один Евгений Капун. Второе место на турнире заняла Наталья Бондаренко, решившая четыре задачи быстрее других и с меньшим числом попыток.
Злые птицы
О постановке задачи расскажет Андрей КАЛИНИН, руководитель подразделения разработчиков Поиска Mail.Ru.
Задача называется «Злые птицы». Суть ее проста. Есть провод конечной длины, на котором располагаются птицы. Некоторые птицы идут направо, некоторые — налево. Когда встречаются друг с другом — меняют направление. Когда доходят до конца провода — взлетают. Нужно определить, когда взлетит каждая из этих птиц. По условиям задачи здесь может быть до 100000 птиц, идущих в каждую сторону, следовательно, суммарно их не более 200000.

Как известно, птицы любят сидеть на проводах. В уездном городе K есть один длинный, особенно полюбившийся им провод. В один прекрасный момент на нем сидело несколько птиц. Все было бы хорошо, да вот только пробежавшая под проводом свинья подняла такую тучу пыли, что очень разозлила птиц.
Став злыми, птицы начали бежать по этому проводу в разные стороны — кто-то налево, кто-то направо. При этом все птицы стали бежать с одинаковой скоростью, равной одному метру в минуту. При встрече двух птиц, двигающихся навстречу друг другу, они немедленно разворачиваются и начинают бежать с той же скоростью в противоположном направлении.
Этот процесс продолжался бы бесконечно долго, но только провод оказался все-таки конечным, и как только какая-та из птиц добегает до конца провода, она тут же взлетает, а все остальные птицы, ошеломленные этим, разворачиваются и начинают бежать в противоположном направлении. Если же до края добегают одновременно две птицы, то происходит два разворота, или, что то же самое, ничего не происходит.
Вам необходимо написать программу, которая по длине провода, начальным позициям и направлениям бега птиц выяснит для каждой птицы, в какой момент времени она улетит с провода.
Формат входных данных
В первой строке задано единственное целое число L (1 ≤ L ≤ 109) — длина провода в метрах.
Во второй строке записано число n (0 ≤ n ≤ 100 000) — количество птиц, бегущих направо. В третьей строке записано n различных целых чисел ai (0 < ai < L) — расстояния в метрах от левого конца провода до птиц, бегущих направо.
В четвертой строке записано число m (0 ≤ m ≤ 100 000) — количество птиц, бегущих налево. В пятой строке записано m различных целых чисел bi (0 < bi < L) — расстояния в метрах от левого конца провода до птиц, бегущих налево.
Никакие две птицы не находятся исходно в одном и том же месте. Гарантируется, что на проводе сидит хотя бы одна птица.Формат выходных данных
В первой строке выведите n целых чисел ti — через сколько минут улетит i-я по порядку описания во вводе птица, бегущая направо. Во второй строке выведите m целых чисел ui — через сколько минут улетит i-я по порядку описания во вводе птица, бегущая налево.
Ограничение по времени – 2 секунды
Ограничение по памяти – 256 мегабайт
В задаче был дан пример. Для разъяснения ее постановки и решения будет полезно отследить движение птиц поминутно на этом примере. В нем даются следующие вводные данные: две птицы находятся на 8-м и 9-м метре и идут вправо, еще три птицы находятся на 2-м, 5-м и 7-м метре и идут влево. Длина провода — 10 метров. Такова начальная ситуация. Нужно рассчитать, когда взлетит какая птица.
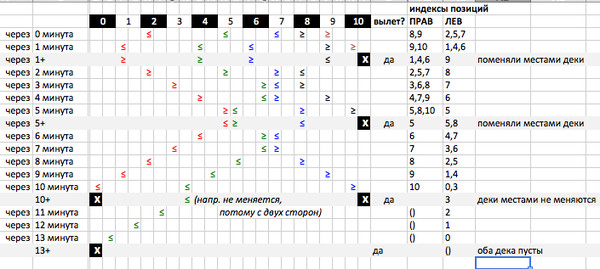
Как видно, на первой и пятой минуте птицы улетают с правого конца, на десятой взлетают сразу две птицы, а на тринадцатой улетает последняя.
Здесь важно отметить, что порядок птиц при этом никогда не меняется. Также обратите внимание на то, что, несмотря на зигзаги, описываемые птицами, число двигающихся влево или вправо птиц не зависит от их столкновения, а характер изменения координат движения всегда остается линейным. Это хорошо заметно по промежутку с первой по пятую минуту, когда произошло аж три столкновения.
Справа в двух колонках я указал позиции птиц. Сразу становится очевидно, что момент первого взлета с провода можно предсказать — число минут (=числу метров) до конца провода от ближайшей к одному из концов птицы.
Также видно, что после взлета все координаты, привязанные к движению направо, становятся координатами, привязанными к движению налево, и наоборот.
В итоге решение задачи сводится к ведению двух деков (deque) – структур данных типа «двунаправленная очередь» (double-ended queue), в которой удаление первого или последнего элемента осуществляется за O(1). При взлете птицы из дека удаляется крайний элемент, а сами деки меняются местами. Храня пары <дек; сколько надо добавить к числам в нем> можно за O(1) находить, через какое время и в какую сторону улетит очередная птица. Поскольку порядок птиц не меняется, дополнительно следует хранить сортированный массив координат оригинального расположения птиц, чтобы определить, какая из птиц покинула провод.
Наиболее красивым решением является решение на Python3:
from collections import deque
length = int(input())
n = int(input())
right = deque(sorted(map(int, input().split())))
m = int(input())
left = deque(sorted(map(int, input().split())))
addLeft, addRight = 0, 0
INF = 2*10**9
ans = 0
while right or left:
L = left[0] + addLeft if left else INF
R = length - (right[-1] + addRight) if right else INF
m = min(L, R)
ans += m
addLeft -= m
addRight += m
if L < R:
left.popleft()
left, addLeft, right, addRight = right, addRight, left, addLeft
elif L == R:
left.popleft()
right.pop()
else:
right.pop()
left, addLeft, right, addRight = right, addRight, left, addLeft
print (ans)
Задачу с птицами первым сделал Михаил КЕВЕР к 22-й минуте с начала раунда. Через несколько секунд задачу сдал Василь БИЛЕЦКИЙ.
Всего с задачей справились 40 человек, начали решение с нее 11 человек. Среднее время на ее решение — 30 минут. Из них самое большое время на решение — 44 минуты (не считая ситуаций, когда решений вообще не прислали). Все 11 человек, успешно решившие первую задачу первой, решили как минимум еще две. За исключением 2 случаев из 11, все они переходили к задаче B, а потом — к задаче C, то есть выполняли задачи в алфавитном порядке. Эта задача на третьем месте среди всех задач, с которых начинали контест.
Трисолианцы
Про задачу про трисолианцев рассказывает Илья ВАЙСМАН, технический директор «Аллоды Онлайн»:
По условию задачи некие жители планеты Трисол обозначают свой возраст не одним целым числом, как мы, земляне, а вектором из k целых чисел. У новорожденного трисолианца вектор возраста состоит из одних нулей, но с каждым годом взросления к каждому элементу вектора возраста прибавляется некоторое положительное число. Историей жизни трисолианца является набор всех векторов возраста, которые у него были в течение жизни. Точно известно, что трисолианцев с одинаковой историей не существует. Ученых интересует, у какого максимального числа трисолианцев история жизни заканчивается на векторе, сумма элементов которого равна n. Нужно написать программу, которая вычисляет это значение по модулю простого числа 7340033 = 7*2^20+1.
К примеру, для k=2 может существовать 8 трисолианцев, история жизни которых заканчивается на векторе с суммой 5.
1. (0, 0) — (1, 1) — (2, 3);
2. (0, 0) — (1, 1) — (3, 2);
3. (0, 0) — (1, 2) — (2, 3);
4. (0, 0) — (1, 4);
5. (0, 0) — (2, 1) — (3, 2);
6. (0, 0) — (2, 3);
7. (0, 0) — (3, 2);
8. (0, 0) — (4, 1).
Недавно стало известно, что жители планеты Трисол обозначают свой возраст не одним целым числом, как мы — земляне, а вектором из k целых чисел. Считается, что у новорождённого трисолианца вектор его возраста состоит из k нулей. По мере взросления, каждый год, к каждому элементу вектора возраста прибавляется некоторое положительное число.
Историей жизни трисолианца называется набор всех векторов его возраста, которые были у него в течение жизни. Земные учёные установили, что не существует двух трисолианцев с одинаковой историей.
Теперь ученых интересует — у какого максимального числа трисолианцев, история жизни заканчивается на векторе, сумма элементов которого равна n. Напишите программу, которая вычисляет это значение по модулю простого числа 7340033 = 7·220 + 1.
Формат входных данных
Первая строка содержит два целых числа n и k — сумма элементов последнего вектора возраста, и количество элементов в векторе (1 ≤ n ≤ 4239, 1 ≤ k ≤ 109).
Формат выходных данных
Выведите максимальное число трисолианцев, история жизни которых может заканчивается на векторе, сумма элементов которого равна n. Ответ следует вывести по модулю 7340033 = 7·220 + 1.
 Маленькая историческая справка, без которой решение задачи, наверное, невозможно. Трисолианцы – жители планеты Трисол, расположенной глубоко внутри Запрещенной Зоны в Галактике Ужаса. Состоят на 100% из жидкости. Способны легко изменять свою форму. Обычные жители миролюбивы, чего нельзя сказать о правящей верхушке. Время от времени друг друга пьют, двигаясь таким способом по карьерной лестнице.
Маленькая историческая справка, без которой решение задачи, наверное, невозможно. Трисолианцы – жители планеты Трисол, расположенной глубоко внутри Запрещенной Зоны в Галактике Ужаса. Состоят на 100% из жидкости. Способны легко изменять свою форму. Обычные жители миролюбивы, чего нельзя сказать о правящей верхушке. Время от времени друг друга пьют, двигаясь таким способом по карьерной лестнице.
Задача относительно простая, потому что все ее решение сводится к комбинаторике. С другой стороны, она сразу становится не столь простой, какой кажется, если всмотреться в возможный диапазон k — размерности вектора (1 ≤ k ≤ 10000000000).
| N=2 | N=3 | N=4 | N=5 | N=6 |
| (0,0) – (1,1) | (0,0) – (1,2) (0,0) – (2,1) |
(0,0) – (1,1) – (2,2) (0,0) – (2,2) (0,0) – (3,1) (0,0) – (1,3) |
(0, 0) — (1, 1) — (2, 3); (0, 0) — (1, 1) — (3, 2); (0, 0) — (1, 2) — (2, 3); (0, 0) — (2, 1) — (3, 2); (0, 0) — (2, 3); (0, 0) — (3, 2); (0, 0) — (4, 1). (0, 0) — (1, 4); |
(0,0) – (1,1) – (2,2) – (3,3) (0,0) – (1,1) – (4,2) (0,0) – (1,1) – (2,4) (0,0) – (1,1) – (3,3) (0,0) – (1,2) – (3,3) (0,0) – (1,2) – (2,4) (0,0) – (2,1) – (3,3) (0,0) – (2,1) – (4,2) (0,0) – (2,2) – (3,3) (0,0) – (3,1) – (4,2) (0,0) – (1,3) – (2,4) (0,0) – (5,1) (0,0) – (1,5) (0,0) – (4,2) (0,0) – (2,4) (0,0) – (3,3) |
| 1 вариант | 2 варианта | 4 варианта | 8 вариантов | 16 вариантов |
Ключевой идеей к пониманию решения является то, что «кусты» для больших значений N частично состоят из решений для меньших значений, что позволяет организовать вычисления через рекурсию.
Графически для частного случая k=2 историю жизни можно отобразить как набор отрезков, соединяющих нулевую отметку с положительными целыми отметками, лежащими на оси на прямой f(x)=n-x.
Вот как выглядит решение для N=4:
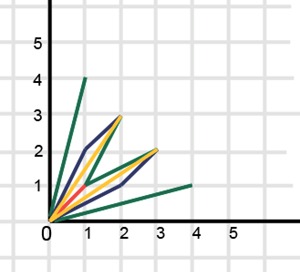
Для N=4 историй — восемь.
Теперь прибавим вектор (1,1) к этой истории и получим
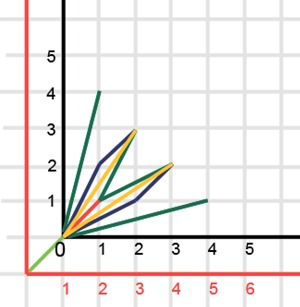
Каждая из историй, начинающихся с вектора (1,1) будет частью истории для N=7. Другой частью истории будут «кусты» поменьше, начинающиеся с вектора (1,2) и т.д.
Аналогичная история с другими векторами. Приведем пример для вектора (1,3), являющегося началом части элементов истории для N=7. В этом случае выйдет следующее:
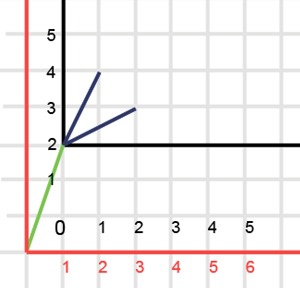
То есть, если мы возьмём вектор, который дали трисолианцу на первый год рождения, и вычтем его из всех векторов истории жизни трисолианца, то после выкидывания этого вектора мы фактически получим некоторую историю жизни трисолианца, у которого сумма элементов последнего вектора равна n − (сумма элементов выкинутого вектора).
Таким образом можно понять что все истории, у которых сумма элементов последнего вектора равна n, могут быть получены из историй с последним вектором, имеющим сумму элементов m для некоторого m < n, добавив некоторый вектор из положительных элементов с суммой, равной n − m ко всей истории жизни.
Сколько же будет таких векторов с суммой, равной n-m? Минимальный вектор включает по единице в каждой координате, следовательно всего векторов, всего компонент k, в итоге выходит сумма n-m-k. Нужно теперь раздать единицы k координатам. Число способов так сделать – число сочетаний с повторениями. Число сочетаний с повторениями рассчитывается как

А число сочетаний без повторений рассчитывается как

Из чего легко выводится, что число сочетаний с повторениями a по b равно числу сочетаний без повторений a + b — 1 по b.
Значит в нашем случае число способов равно C из n — m — k + k — 1 по
k, то есть C из n — m — 1 по k.

Обозначив искомую величину как ansn, получается следующая рекуррентная формула:. Предполагается, что ans0 = 1. Время работы алгоритма составит O(n2).

где C(x,y) — число сочетаний второго аргумента по первому, рассчитывается как x! / (x-y)! / y!
Задачу про трисолианцев сделали почти все из присутствовавших на финале (кроме двух человек). На решение задачи ушло примерно 18 минут. Первым ее сделал Роман РИЗВАНОВ на 11 минуте, с небольшим отрывом – Евгений КАПУН.
Процессор
Про задачу о процессоре расскажет Александр ГОРНЫЙ, CIO Mail.Ru Group:
В задаче фигурирует некий двухъядерный процессор, умеющий выполнять 26 различных инструкций. Каждая инструкция символически записывается буквой английского алфавита. Программы состоят из набора инструкций. Нужно рассчитать, какое минимальное время понадобится процессору для обработки указанных 2n программ (в свою очередь состоящих из указанной последовательности конкретных инструкций), если известно, что из-за особенности архитектуры в двух ядрах могут выполняться только одинаковые инструкции в один момент, и известно n — количество таких процессоров.
Иллюстрация того, как процессор может обрабатывать две программы одновременно:
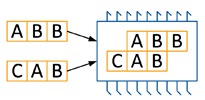
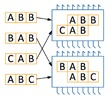
Задача сводится к тому, как эффективно разбросать 2n программ по n процессорам и двум ядрам в каждом так, чтобы количество шагов было минимальным.
Как известно, большинство производимых сейчас процессоров являются многоядерными, то есть поддерживают выполнение нескольких инструкций одновременно. Компания Paraltel разработала новый тип двухядерного процессора, который позволяет выполнять 26 различных инструкций, обозначаемых заглавными латинскими буквами. Исполнение каждой такой инструкции требует ровно одного такта работы процессора.
Программа для этого процессора представляет собой последовательность инструкций. Инструкции программы должны быть исполнены в том порядке, в котором они следуют в программе, менять местами инструкции не разрешается.
Благодаря наличию двух ядер, процессор может одновременно исполнять две программы — по одной на каждом ядре. Однако из-за особенностей архитектуры одновременно на двух ядрах одного процессора могут выполняться только одинаковые инструкции.
При выполнении двух программ на процессоре специальное управляющее устройство оптимизирует выполнение так, чтобы завершить выполнение обеих программ как можно раньше. Например, программы «ABB» и «ABC» можно выполнить на процессоре за 4 такта: сначала одновременно выполняются команды «A» обеих программ на разных ядрах, затем одновременно команды «B», затем команда «B» из первой программы и, наконец, «C» из второй. Аналогично, программы «CAB» и «BAB» выполняются за 4 такта.
Недавно специалисты компании собрали из n процессоров суперкомпьютер, на котором требуется выполнить 2n программ. Организация вычислений такова, что каждый процессор должен выполнить ровно по две программы из этого набора, по одной на каждом ядре.
Вам необходимо спланировать выполнение 2n программ на n процессорах так, чтобы время завершения выполнения всех программ было минимальным.
Формат входных данных
В первой строке задано число n (1 ≤ n ≤ 10) — количество процессоров. Далее, в 2n строках заданы программы, которые необходимо выполнить. Каждая программа содержит от 1 до 100 команд. Каждая команда задается заглавной латинской буквой.
Формат выходных данных
Выведите единственное число — минимальное время, за которое можно выполнить все программы.
В качестве примера к задаче приводится набор следующих программ: ABB BAB CAB ABC
и информация, что процессоров два.
Вот такие четыре шага нужны для выполнения программы на двух процессорах:
| Процессор 1 ядро 1 | Процессор 1 ядро 2 | Процессор 2 ядро 1 | Процессор 2 ядро 2 |
| [A]BB | [A]BC | [B]AB | |
| A[B]B | A[B]C | [C]AB | |
| AB[B] | B[A]B | C[A]B | |
| AB[C] | BA[B] | CA[B] |
Разобьем решение задачи на два этапа и рассмотрим каждый в отдельности.
Первым этапом будет построение графа. Вершинами его являются 2n программ, которые нам необходимо выполнить. Граф будет взвешенным, и вес ребра между двумя программами равен количеству времени, которое процессор потратит на их совместное выполнение. Это значение равно сумме длин программ минус те команды, которые будут выполняться одновременно. А таких команд не больше, чем LCS(a, b), где a и b — строки, описывающие программы, а LCS (Longest Common Subsequence, наибольшая общая подпоследовательность) — функция, находящая наибольшую общую подпоследовательность двух последовательностей.
В итоге функция нахождения веса ребра будет выглядеть следующим образом:
int dist(String a, String b) {
int[][] d = new int[a.length() + 1][b.length() + 1];
for (int[] ar : d) { Arrays.fill(ar, 1000000000); }
d[0][0] = 0;
for (int i = 0; i <= a.length(); ++i) {
for (int j = 0; j <= b.length(); ++j) {
if (i < a.length()) {
d[i + 1][j] = Math.min(d[i + 1][j], d[i][j] + 1);
}
if (j < b.length()) {
d[i][j + 1] = Math.min(d[i][j + 1], d[i][j] + 1);
}
if (i < a.length() && j < b.length() && a.charAt(i) == b.charAt(j)) {
d[i + 1][j + 1] = Math.min(d[i + 1][j + 1], d[i][j] + 1);
}
}
}
return d[a.length()][b.length()];
}
Вторым же этапом решения будет нахождение в этом графе совершенного паросочетания, в котором вес максимального ребра минимизирован. Одним из самых простых алгоритмов, решающих эту задачу и укладывающихся в ограничения по времени, является динамическое программирование, но уже по подмножествам. Пусть для каждого набора вершин размера не более, чем k, мы знаем ответ. В таком случае перебрав все такие наборы и добавив к каждому все возможные ребра, еще в нем не лежащие, мы сможем посчитать ответ для всех наборов размера не более, чем k + 2.
int[] d = new int[1 << (2 * n)];
Arrays.fill(d, 1000000000);
d[0] = 0;
for (int mask = 0; mask + 1 < 1 << (2 * n); ++mask) {
if (d[mask] == 1000000000) {
continue;
}
int i = 0;
while ((mask & (1 << i)) != 0) {
++i;
}
for (int j = i + 1; j < 2 * n; ++j) {
if ((mask & (1 << j)) == 0) {
d[mask | (1 << i) | (1 << j)] = Math.min(d[mask | (1 << i) | (1 << j)], Math.max(d[mask], dist[i][j]));
}
}
}
Задачу «Процессор» сделали почти все из присутствующих на финале (кроме двух человек). Среднее время решения этой задачи — около 18 минут. Первым решил задачу Владислав ЕПИФАНОВ на 11-й минуте.
Осада
О задаче «Осада» расскажет Павел КРОТКОВ, студент кафедры НИУ ИТМО.
Задача рассказывает о сказочном городе Альдерсберг, на который вот-вот наступят полчища врагов. Для того, чтобы удержать город, нужно поставить барьер из n артефактов, и активировать каждый i-й артефакт магической энергией в объеме a[i] «мерлинов». После этого, используя b[i] «мерлинов», враг сможет разрушить этот артефакт на расстоянии. Защитники города располагают A мерлинами магической энергии, в арсенале противника — B мерлинов. Горожане решили активировать артефакты так, чтобы после их разрушения магами противника максимальное число артефактов осталось активно. Нужно помочь защитникам города выбрать, какие артефакты нужно активировать.
Для славного города Альдерсберг настали тяжелые времена. С минуты на минуту несметные полчища врагов пойдут на штурм. Только магические барьеры могут помочь удержать город.
В арсенале защитников города имеется n артефактов, позволяющих поставить барьер. Для активации i-го артефакта требуется ai мерлинов (единиц магической энергии). После этого, используя bi мерлинов, противник может разрушить артефакт на расстоянии.
Защитники города располагают A мерлинами магической энергии, в арсенале противника B мерлинов. Запасы магической энергии не восполняются. Горожане решили активировать артефакты так, чтобы после их разрушения магами противника, максимальное число осталось активно.
Помогите защитникам города выбрать, какие артефакты нужно активировать.
Формат входных данных
Первая строка содержит три целых числа A, B и n (0 ≤ A, B ≤ 105, 0 ≤ n ≤ 1000), разделенных пробелами. Следующие n строк содержат пары чисел ai и bi (1 ≤ ai, bi ≤ 105).
Формат выходных данных
В первой строке выведите число артефактов, которые останутся активны при оптимальных действиях обеих сторон конфликта. Во второй строке выведите число артефактов, которые должны активировать защитники города, и номера этих артефактов. Числа в одной строке разделяйте пробелами.
Артефакты занумерованы, начиная с единицы, в порядке, в котором они заданы во вводе.
 Маленькая историческая справка. Альдерсберг — второй по величине город в одно из четырех Северных Королевств, Аэдирне, расположенное на самом краю мира. Город Альдерсберг был построен вокруг стен крепости, которая охраняла границы Аедирна (Анджей Сапковский)
Маленькая историческая справка. Альдерсберг — второй по величине город в одно из четырех Северных Королевств, Аэдирне, расположенное на самом краю мира. Город Альдерсберг был построен вокруг стен крепости, которая охраняла границы Аедирна (Анджей Сапковский)
Предположим, что защитники города активировали некоторое множество артефактов. Оптимальной стратегией для их врагов будет разрушать их в порядке увеличения bi. Действительно, цель врага — разрушить как можно больше артефактов. Нет смысла тратить много энергии на трудноуничтожимый артефакт, пока есть легкая цель.
Перенумеруем артефакты в порядке неубывания bi. Пусть стало известно, что первый артефакт, который враг не сможет уничтожить при оптимальных действиях защитников, имеет номер k. Опишем действия защитников, исходя из этого предположения. Из первых k−1 артефактов надо выбрать несколько так, чтобы суммарная энергия, затрачиваемая на их разрушение, составила не менее B−bk+1 мерлинов, а энергия на активацию была минимальна. Активируем k-й артефакт. Наконец, последние n−k артефактов активируем в порядке возрастания энергозатрат.
К сожалению, k заранее не известно. Будем перебирать номер первого артефакта, который враг не сможет уничтожить, и строить оптимальный ответ для этого предположения.
Пусть Dij — минимальная энергия, которая потребуется на активацию артефактов с номерами не более i (до 1000), таких что для их разрушения потребуется j мерлинов магической энергии (до 100000). Переход: Di,j = min(Di−1, j, Di−1, j−bi + ai). Эти два случая соответствуют тому, надо ли активировать артефакт номер i для достижения оптимального Dij.
По массиву D находим энергию, необходимую для того, что противник не смог уничтожить k-й артефакт. После этого жадно берем остальные, пока хватает энергии на активацию. В итоге, перебрав все k находим оптимальный ответ.
Время работы описанного подхода – O(n(B + n)). Для того, чтобы превратить его в полноценное решение, надо добавить хранение информации для восстановления ответа, что не влияет на асимптотику.
Узким местом в решении могла стать используемая память. Заметим, что у массива D можно хранить только последнюю строку. Кроме того, для каждой пары (i, j) достаточно знать, надо ли активировать артефакт номер i для достижения оптимального Dij. Для того, чтобы уложиться в ограничения по памяти надо было использовать не более двух байт для хранения этого бита информации.
Задачу «Осада» решило 19 человек. Быстрее всех с этой задачей справился Петр МИТРИЧЕВ на 87-й минуте (перед задачей «Осада» Петр успешно сдал три первые).
Перемешивание колоды
О задаче про перемешивание колоды рассказывает Сергей МЕЛЬНИКОВ, студент НИУ ИТМО:
В этой задаче нужно продумать механизм перемешивания колоды, позволяющий за минимальное число перемещений блоков карт из середины в конец колоды идеально ее перемешать (то есть сделать так, чтобы никакие две одинаковые карты не шли друг за другом), либо сообщить, что идеально перемешать колоду невозможно. Изначально колода отсортирована по неубыванию достоинства. Дано количество разных достоинств карт, порядок карт в колоде, количество колод.
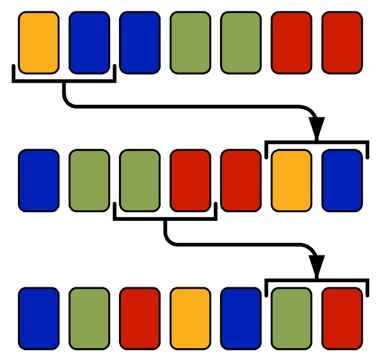
Автоматизация и компьютеризация стремительно вторгаются во все сферы нашей жизни. Посудомоечные машины, бортовые компьютеры в автомобилях, электрические мухобойки — все эти приспособления в той или иной степени облегчают человеку стандартные привычные действия. В этой же задаче от вас потребуется автоматизировать еще одно привычное многим действие — перемешивание колоды карт.
Рассмотрим новую колоду карт, карты в которой имеют некоторую характеристику, которая представляет собой целое число от 1 до t. Будем называть ее достоинством карты, несколько карт в колоде могут иметь одно и то же достоинство.
Исходно карты в колоде отсортированы по неубыванию достоинства. Соответственно, первая карта в колоде имеет достоинство 1, а последняя — достоинство t. При этом достоинства двух соседних карт в колоде отличаются друг от друга не более, чем на один, и достоинство каждой следующей карты не меньше достоинства предыдущей.
Будем называть колоду хорошо перемешанной, если никакие две идущие подряд карты не имеют одинаковое достоинство.
Для перемешивания колоды используется устройство, которое способно выполнять действия следующего типа: для некоторых i и j взять карты, которые находятся на позициях с i-й по j-ю включительно и переместить их в конец колоды в том же порядке.
Вам необходимо написать программу, которая по описанию исходной колоды составит последовательность из минимального количества указанных действий, в результате выполнения которых колода окажется хорошо перемешанной.Формат входных данных
В первой строке содержится одно целое положительное число x — количество колод, которые необходимо отсортировать. Далее идут описания x колод.
Описание каждой колоды состоит из двух строк. В первой строке описания колоды находится целое положительное число n — количество карт в колоде. В следующей строке содержатся n натуральных чисел, описывающие достоинства карт в колоде. Первое число в такой строке всегда равно единице, каждое следующее не меньше предыдущего и отличается от него не более, чем на 1.
Суммарное количество карт во всех колодах во вводе не превышает 200000.
Формат выходных данных
Для каждой колоды, данной во вводе, выведите «-1», если перемешать ее, используя описанные в условии действия, невозможно. Если же алгоритм перемешивания существует, то в первой строке его описания выведите k — минимальное количество действий, которое требуется для перемешивания колоды. В следующих k строках выведите действия, каждое из которых описывается двумя числами i и j — позициями карт, ограничивающих отрезок, который необходимо переместить в конец.
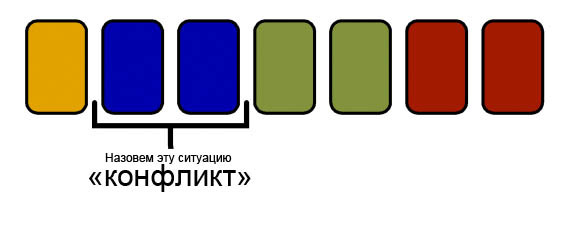
Назовем конфликтом, ситуацию, в которой две одинаковые карты стоят подряд:
Назовем телом исходную последовательность карт, которую постепенно будем уменьшать, перенося карты в хвост. Хвост будет формироваться таким образом, что бы карты в нем не образовывали конфликтов.
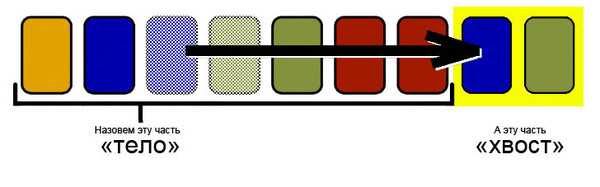
Преобразуем исходную последовательность в последовательность конфликтов и будем работать с новой последовательностью. Будем называть цветом конфликта число написанное на карточках, его образующих. Каждый раз перенося отрезок карт в конец колоды, будем выбирать его концы внутри конфликтов.
Обозначим число конфликтов через K. Поскольку одна операция перемещения убирает не более двух конфликтов, задачу невозможно решить быстрее чем за ⌈K / 2⌉ операций (здесь и далее в описании встречаются конструкции ⌊…⌋ и ⌈…⌉ — это округление вниз и вверх соответственно).
Обозначим как M максимальное число конфликтов одного цвета и будем называть сами эти конфликты «максимальными». Научимся решать задачу в случае, когда M = ⌈K / 2⌉.
Также напомню, что по условиям задачи колода отсортирована по неубыванию достоинства.
К примеру, в колоде 1122333344 число М будет равно 3 (три конфликта 33), общее число конфликтов – 6. В данном случае M = ⌈K / 2⌉.
В рассматриваемом случае (не примере) есть два варианта:
- K — четное (как в примере). Покрасим все конфликты, предшествующие «максимальным» в цвет A, «максимальные» конфликты в цвет B, а следующие за ним — в цвет C. |A| + |B| + |C| = |K|, следовательно |A| + |C| = |B| = M. В приведенном выше примере цветовая раскраска для 1122333344 будет AABBBC.
Будем ликвидировать конфликты парами: сначала пары (B, C), потом, когда таких пар не останется — пары (A, B). Отметим, что хвост будет иметь вид (B, C)* (A, B)*, где * — одно или более повторение.
В нашем примере это:
1122333344 (AABBC) ->1122333-4.34 (AAB) -> 1-2333-4.3412 (BB)(дефисы обозначают места, откуда взяты карты перед переносом в хвост. Точка – разделитель тела и хвоста)
Очевидно, два конфликта одного цвета подряд не идут. При сопряжении с телом тоже все будет хорошо: если |C| > 0, то последняя карточка со значением C останется на месте, а хвост будет начинаться с B. Если же |C| = 0, то хвост имеет вид (A, B)*, при этом последняя карточка со значением B останется на месте.
- K — нечетное. Применим аналогичную раскраску. Если есть хотя бы одна карточка цвета A, то сведем задачу к предыдущему случаю, добавив в начало виртуальную карточку и A-конфликт. Если есть карточка цвета C, то добавим новую виртуальную карточку и C-конфликт в конец, опять сведя к предыдущему случаю.
Решения для этих случаев оптимальны, так как достигается нижняя граница числа операций ⌈K / 2⌉. Итого, мы умеем оптимально решать задачу, когда число «максимальных» конфликтов составляет половину всех конфликтов (с округлением вверх). Будем называть такой случай базовым.
Теперь классифицируем исходные ситуации по максимальному числу карточек одного достоинства подряд. Будем называть эти карточки максимальными и обозначим их количество как Q.
- Q = 0. Конфликты отсутствуют, ничего делать не надо.
- Если Q > ⌈N / 2⌉, то задача не имеет решения. В этом случае, у нас есть менее Q−1 не максимальных карточек, чего не достаточно для разделения карточек максимального достоинства.
- Q = ⌈N / 2⌉. В этом случае не максимальных карточек хватает, но каждая вторая карточка должна быть максимальной. Покрасив карточки в три цвета получим:
- a A-карточек идущих до максимальных,
- b = Q B-карточек являющихся максимальными
- c C-карточек после максимальных.
При этом будем считать, что все A- и C-карточки образуют конфликты Рассмотрим следующие случаи
- a = 0. Следовательно c = N − Q = ⌊N / 2⌋, и, следовательно, b отличается от c не более чем на единицу, то есть мы свели к базовому случаю.
- с = 0. Аналогично предыдущему случаю.
- a > 0, b > 0 Среди А-карточек a − 1 конфликт, среди B: b − 1, среди C: c − 1. (a − 1) + (c − 1) = N − Q − 2, отличается от Q − 1 не более чем на единицу, а это значит, что это базовый случай.
- M < ⌊ ( N + 1) / 2 ⌋. Если можно добавить некоторое количество виртуальных конфликтов (конфликтов между карточками с разными значениями), чтобы задача свелась к базовому случаю, то добавим их и решим как базовый случай.
Теперь будем каждый раз удалять последнюю пару конфликтов, которую можно удалить (два последних конфликта разного цвета) (C1, C2). Если в процессе попадем в базовый случай, то будем решать, так как решаем его. Если больше конфликтов не осталось, то задача решена.
Докажем, что новых конфликтов не возникнет. Рассмотрим цвет последнего конфликта Z, мы будем переносить пары конфликтов (X, Z) пока Z не кончится, при этом на конце останется Z и получим хвост Z (X1, Z) (X2, Z)…. Если Z-конфликты кончатся, то будет переход на (X, Y) конфликты, то есть пара (Xk, Z) (Xk+1, Y), при Xk+1 ≠ Z.
При переходе к базовому случаю конфликтов не возникнет, потому что после переноса пары (X, Z) ни X ни Z не могут стать максимальными (M). Так как M ≠ Z, то либо Z кончились и конфликта (X, Z) (Z, ...) не возникнет, либо Z находится после M, то есть получим продолжение (X, Z) (M, Z).
Так как мы на каждом шаге удаляем пару конфликтов, либо используем базовый случай случай, то построенное решение оптимально и работает за ⌈K / 2⌉ операций.
Можно заметить, что нет необходимости хранить информацию о том, какие числа и в каком порядке записаны в хвосте, поскольку там нет конфликтов. Последовательность значений можно поддерживать при помощи декартового дерева по неявному ключу, при этом суммарное время работы составит O(N log N). Также, если в какой-то момент мы определяем, что в конце тела нет конфликтов, то можно уменьшить длину тела и соответственно увеличить хвост. Можно рассмотреть все случаи, когда происходит перемещение отрезка, и убедиться, что тело всегда будет иметь вид: префикс исходного массива с не более чем двумя вырезанными подотрезками. Основываясь на этом факте можно реализовать решение за O(n), но для решения данной задачи в данных ограничениях этого не требуется.
Задачу «Перемешивание карт» решил только Евгений КАПУН.
Гоночная трасса
По условию задачи в некому уездном городе N построили новую гоночную трассу. Трасса полностью готова к эксплуатации, необходимо лишь зарегистрировать ее во Всемирном Реестре Гоночных Трасс, но для этого необходимо выяснить ее протяженность.
Трасса представляет собой пространство, ограниченное внешним и внутренним краями трассы. Будем называть простой замкнутую ломаную, не имеющую самопересечений и самокасаний. И внешний, и внутренний края являются произвольными простыми замкнутыми ломаными, при этом ломаная внутреннего края находится строго внутри многоугольника, образованного внешним краем трассы. Траекторией движения по трассе является любая простая замкнутая ломаная, содержащаяся в многоугольнике внешнего края трассы, при этом содержащая в образованном ею многоугольнике внутренний край трассы.
Траектория может иметь общие точки как с внутренним, так и с внешним краями трассы.
Протяженностью трассы, согласно правилам Всемирного Реестра Гоночных Трасс, является длина кратчайшей траектории движения по трассе.
Необходимо написать программу, которая по описанию внутреннего и внешнего краев трассы будет находить протяженность трассы.
Число звеньев ломаной внешнего и внутреннего края трассы может быть от 3 до 258 включительно, координаты вершин задаются целыми числами от –1000 до 1000, Ломаные не имеют общих точек и заданы в порядке обхода против часовой стрелки.
Буквальную постановку задачи можно посмотреть на официальном сайте Russian Code Cup.
Эта задача — про планиметрию и про работу с графом вершин краев трассы.
Разобьем решение задачи на два этапа и рассмотрим каждый в отдельности.
Первым этапом будет построение графа, вершинами которого являются все вершины краев трассы. Две вершины соединяются ребром, если отрезок, проведенный между вершинами, не выходит за пределы трассы. Граф будет взвешенным, и вес ребра между двумя вершинами будет равен расстоянию между ними.
Для построения графа необходимо проверять, не покидает ли отрезок пределы трассы. Это можно сделать, пересекая отрезок со всеми звеньями обеих ломаных.
Также стоит обратить особое внимание на случай, когда отрезок выходит за пределы трассы в вершине ломаной. Чтобы избежать этого, можно считать, что отрезок, за исключением своих концов, не должен иметь общих точек с краями трассы.
Еще одним случаем недопустимого отрезка является отрезок, полностью лежащий в многоугольнике внутреннего края трассы или вне многоугольника внешнего края. Отсечь такие отрезки можно, если аккуратно рассмотреть углы, под которыми из одного из концов отрезка выходят сам отрезок и два звена соответствующей этому концу ломаной.
Самая левая вершина внутреннего края трассы всегда будет лежать на оптимальной траектории, причем будет являться левой точкой оптимальной траектории. Из графа требуется исключить все вершины левее этой, а саму вершину раздвоить. При этом ребра необходимо разделить между двумя копиями вершины в соответствии с тем, выше или ниже звеньев ломаной внутреннего края они находятся. Это также можно выполнить рассматривая углы при вершине.
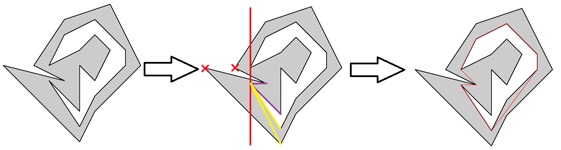
Вторым же этапом решения будет нахождение в этом графе кратчайшего пути между двумя копиями разделенной вершины. Кратчайший путь и будет являться оптимальной трассой, а его длина — протяженность трассы. Кратчайший можно находить с помощью алгоритма Дейкстры.
Построение графа занимает O(n3) времени, так как каждое из O(n2) возможных ребер необходимо пересечь с O(n) звеньями ломаной. Время поиска кратчайшего пути в графе с O(n) вершинами и O(n2) ребрами составляет O(n2). Таким образом, суммарное время работы программы составляет O(n3).
Задачу «Гоночная трасса» успешно решило пять человек. Первым из них был Владислав ЕПИФАНОВ, он сдал задачу на 93-й минуте после успешного решения первых трех.
Это задачи финала Russian Code Cup 2012. Для того, чтобы пройти в финал, нужно было решить задачи, предложенные на одном из трех квалификационных онлайн-этапов (они были сильно проще, я публиковал разборы по первому, второму и третьему квалификационным раундам ), а после выхода в первые две сотни лучших – на отборочном онлайн-раунде (разбор) попасть в лучшие пятьдесят участников. Многие из задач, сформулированные в игровой форме, являются аналогами настоящих проблем, возникающих в реальном мире. Конечно, мы не могли сообщить вам настоящее название планеты Трисол или секретного города Альдерсберг, но мы рады, что мы им помогли, правда?
Алиев Рауф
директор по исследованиям и образованию
Mail.Ru Group
Автор: raliev