
Кому интересно, как в несколько строк кода на С++ смоделировать вот такой параметрический бревенчатый домик — прошу под кат.
Уже несколько лет используем в своих проектах бесплатную версию библиотеки твердотельного моделирования sgCore (вот небольшой обзор возможностей). Недавно авторы выпустили версию для iOS, и, так как данная платформа активно развивается, то, думаю, небольшой вводный пример в данную библиотеку будет многим интересен. Хочу показать на небольшом примере, как с её помощью сделать довольно сложную модель всего за несколько шагов.
Вот исходники демо проектов для этой статьи
iOS
mac
win
Создадим модель параметрического бревенчатого дома. Чтобы не усложнять, введем всего три параметра — радиус сечения бревна, ширина дома и длина дома. Понятно, что в реальных задачах количество параметров будет гораздо больше, но в данном примере введение новых параметров ничего нового не внесет. Таким образом, нам необходимо построить такую модель дома, которая будет перестраиваться вызовом всего одной функции
void Build(sgFloat log_size, sgFloat houseSizeX, sgFloat houseSizeY);
Для начала проинициализируем ядро библиотеки. Это необходимо делать один раз в главном потоке до первого использования функций sgCore:
sgInitKernel();
Первым нашим шагом будет построение сечения бревна. Для того, чтобы бревна не просто лежали друг на друге, а образовывали более-менее стабильную конструкцию, сделаем форму сечения не круглой, а состоящей из двух дуг:

Бревно аналогичного сечения можно получить двумя способами — или создав само плоское сечение и использовать операцию выдавливания плоского контура, или создать два цилиндра одинакового радиуса, сместить один из цилиндров и применить операцию булевого вычитания. Так как операция выдавливания более быстрая, чем булево вычитание — поэтому воспользуемся первым способом.
Создадим сечение из двух дуг. Для плотного прилегания бревен друг к другу, данные дуги должы быть одинакового радиуса:
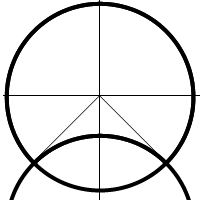
Для создания двух дуг, нам необходимо вычислить точки пересечения двух окржностей одинакового радиуса. Данный радиус является одним из параметров нашей модели — поэтому функция построения контура бревна будет иметь один входной параметр — радиус бревна
void BuildLogSection(sgFloat log_size);
Создадим первую дугу сечения по трем точкам:
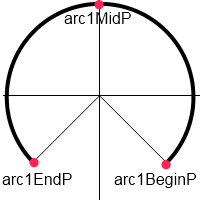
Пусть угол, который задает пересечение этих двух окружностей, будет равен 45 градусам. Тогда точки, задающие первую дугу, будут иметь следующие координаты:
SG_POINT arc1BeginP = {log_size*cosCalc, -log_size*sinCalc, 0};
SG_POINT arc1EndP = {-log_size*cosCalc, -log_size*sinCalc, 0};
SG_POINT arc1MidP = {0, log_size, 0};
Где log_size — радиус бревна, а sinCalc и cosCalc — синусы и косинусы угла, который, как мы договорились, равен 45 градусам. Задавая различные углы, можно получить огромное количество различных вариантов сечений, состоящих из двух дуг.
Создадим структуру дуги по трем этим точкам:
SG_ARC arc1;
arc1.FromThreePoints(arc1BeginP, arc1EndP, arc1MidP, false);
Первые три аргумента — вычисленные точки, последний агрумент — инвертировать или нет дугу, заданную тремя точками. Если данный параметр равен false, то средняя точка дуги будет лежать на создаваемой нами дуге, если true, то создасться дуга, которая дополняет созданную первым способом дугу до полной окружности.
Вторую дугу создадим другим способом — по двум конечным точкам, нормали к плоскости дуги и радиусу. Конечные точки второй дуги совпадают с конечными точками первой, нормаль к плоскости дуги — это ось Z, то есть вектор (0,0,1), а радиус — такой же как и у первой дуги, то есть log_size. Строим структуру второй дуги:
SG_ARC arc2;
arc2.FromBeginEndNormalRadius(arc1BeginP, arc1EndP, zAxe, log_size, false);
Далее нам необходимо построить сами объекты геометрического ядра — наследники sgCObject. Для дуг это будут объекты класса sgCArc. Так как мы в дальнейшем будем по этим дугам строить контур, то сразу сохраним наши дуги в массив:
sgCObject* acrsObjs[2];
acrsObjs[0] = sgCArc::Create(arc1);
acrsObjs[1] = sgCArc::Create(arc2);
И создадим сам контур, который в дальнейшем будем использвать для построения бревна:
m_log_section = sgCContour::CreateContour(acrsObjs, 2);
После того, как сечение построено, мы можем создать бревно. Так как нам нужно создавать бревна различной длины, то создадим функцию, выдавливающую наше сечение на произвольную длину.
sgC3DObject* BuildLog(sgFloat logH);
Так как мы создали плоский контур, в плоскости XOY, то выдавливать контур сечения бревна будем по оси Z (перпендикулярно плоскости сечения):
SG_VECTOR extrVect = {0,0, logH};
sgCObject* logObj = sgKinematic::Extrude(*m_log_section, NULL, 0, extrVect, true);
Первый агрумент функции выдавливания — внешний контур, который выдавливаем, второй аргумент — массив отверстий в выдавливаемом объекте — так же плоские контура, которые лежат внутри внешнего контура, третий аргумент — количество отверстий. Так как в бревнах, из которых строят дом, сквозных отверстий по всей длине бревна нет, то эти два аргумента у нас нулевые. Четвертый агрумент — вектор выдавливания — он у нас направлен по оси Z и имеет длину — logH — аргумент функции создания бревна. Последний аргумент — замыкать создаваемый объект до твердого тела или просто создавать боковую поверхность выдавливания. Другими словами — нужно нам создавать «донышки» или нет. У нас он равен true.
Давайте создадим первое бревно произвольной длины и добавим его в нашу сцену:
sgGetScene()->AttachObject(BuildLog(houseSizeX));
После запуска программы мы увидим пустую сцену. Где бревно???
На самом деле бревно создалось и оно будет отрисовываться, если вы используете для отрисовки не массив треуголников объекта, а его каркасную модель. Пока у нашего бревна нет треугольников — поэтому мы ничего и не увидели.
Для того, чтобы у трехмерного объекта появилось представление в виде треугольников — объект необходимо триангулировать. Это можно делать автоматически для всех создавамых трехмерных объектов, или вручную для каждого объекта. Для автоматической триангуляции необходимо включить флаг:
sgC3DObject::AutoTriangulate(true, SG_DELAUNAY_TRIANGULATION);
Второй аргумент — это тип триангуляции. Подробнее виды триангуляции описаны в документации к sgCore.
Но здесь есть одна тонкость. Триангуляция очень сложных объектов может занимать некотороое время. А для использования и работы с объектами само триангулирование не нужно — оно необходимо только для визуализации конечного результата. Поэтому если вы строите сложные объекты, как промежуточные, то следует отключить автоматическую триангуляцию и триангулировать уже конечные результаты, которые и увидит пользователь. Так как у нас будет множество сложных операций до получения конечного результата — поэтому выключим автоматическую триангуляцию и будем триангулировать вручную только те объекты, которые действительно необходимо визуализировать.
Поэтому немного преобразуем создания нашего бревна:
sgC3DObject* log1 = BuildLog(houseSizeX);
log1->Triangulate(SG_DELAUNAY_TRIANGULATION);
Вот что получаем:

Следующим шагом будет построение пазов для каждого создаваемого бревна. Пазы — это углубления в бревне в тех местах, где к бревну будет прилегать другое бревно. Построим в наших бревнах пазы там, где к нему будут прилегать бревна, на которых лежит данное бревно, учитывая отступы, принятые при строителстве бревенчатых домов.
Для этого расширим функцию построения бревна, введя новые параметры:
sgC3DObject* BuildLog(sgFloat logH, bool withGroove, sgFloat logH, bool withGroove, sgFloat groove_size, sgFloat grooveShift);
withGroove — флаг, надо ли вообще строить паз
groove_size — радиус паза (равен радиусу бревна)
grooveShift — отступ от края бревна, на котором будет строиться паз.
Паза будет два — с обоих концов бревна.
Для построения пазов будем использовать булево вычитание. Для скорости работы, вычитаемый объект будет цилиндром. Можно использовать, конечно, и другое бревно, но, так как бревна будут пересекаться таким образом, что относительно друг друга они могут считаться цилидрами (выемка, образованная второй дугой выдавливаемого контура, в процессе построения паза не участвует), то будем вычитать цилиндр.
Создадим два цилиндра радиуса равным радиусу бревна, произвольной длины (длина этого временного объекта не имеет значения, ни на скорость работы, ни на результат это не влияет). Самое главное на этом шаге — правильно разместить эти временные объекты в простанстве. Так как наше бревно основанием стоит на плоскости XOY и направлено по оси Z, то и эти временные объекты мы должны разместить соотвествующим образом. Цилиндры, как объекты-примитивы, так же создаются с основанием на плоскости XOY, с центорм в начале координат и направлены по оси Z. Таким образом, нам сначала необходимо повернуть наши временные объекты вокруг оси Y, потом сдвинуть так, чтобы учитывалась глубина паза (у нас это будет половина толщины бревна — то есть как раз параметр log_size) и отступы от краев бревна. Таким образом создание этих временных объектов будет выглядеть так:
if (withGroove)
{
sgFloat cylH = 10*groove_size;
sgC3DObject* cyl1 = sgCreateCylinder(groove_size, cylH, 24);
cyl1->InitTempMatrix()->Rotate(zeroP, yAxe, 90.0*M_PI/180.0);
SG_VECTOR transVect = {-cylH/2, -groove_size, grooveShift};
cyl1->GetTempMatrix()->Translate(transVect);
cyl1->ApplyTempMatrix();
cyl1->DestroyTempMatrix();
sgC3DObject* cyl2 = sgCreateCylinder(groove_size, cylH, 24);
cyl2->InitTempMatrix()->Rotate(zeroP, yAxe, 90.0*M_PI/180.0);
transVect.z = logH-grooveShift;
cyl2->GetTempMatrix()->Translate(transVect);
cyl2->ApplyTempMatrix();
cyl2->DestroyTempMatrix();
}
Эти объекты триангулировать не нужно, но давайте временно сделаем это и добавим в сцену, просто чтобы посмотреть — так ли мы их разместили:

Отлично. Объекты размещены так, как нужно. Уберем из кода триангуляцию этих объектов и не будем добавлять их в сцену.
Далее необходимо использовать булево вычитание для получения бревна в пазами.
Сначала вычтем первый временный объект. Так как в результате булевого вычитания создается группа, то там её надо развалить, удалить объект группы и переназначить указатель на бревно на первый (и единственный объект из разваленной группы). При этом не забудем удалить тот временный цилиндр, так как он нам больше не нужен, а так же старый объект бревна:
sgCGroup* boolRes1 = sgBoolean::Sub((const sgC3DObject&)(*logObj), *cyl1);
int ChCnt = boolRes1->GetChildrenList()->GetCount();
sgCObject** allChilds = (sgCObject**)malloc(ChCnt*sizeof(sgCObject*));
boolRes1->BreakGroup(allChilds);
sgCObject::DeleteObject(boolRes1);
sgCObject::DeleteObject(logObj);
logObj = allChilds[0];
sgCObject::DeleteObject(cyl1);
Аналогично поступим со вторым верменным цилиндром:
boolRes1 = sgBoolean::Sub((const sgC3DObject&)(*logObj), *cyl2);
ChCnt = boolRes1->GetChildrenList()->GetCount();
allChilds = (sgCObject**)malloc(ChCnt*sizeof(sgCObject*));
boolRes1->BreakGroup(allChilds);
sgCObject::DeleteObject(boolRes1);
sgCObject::DeleteObject(logObj);
logObj = allChilds[0];
sgCObject::DeleteObject(cyl2);
После этих двух операций получаем следующий результат:

Следующим шагом будет создание стен. По сути, ничего нового этот шаг не приносит — мы просто должны создать нужное количество бревен и разместить их в соотвествующих местах. Скажем только, что для создания одинаковых бревен будем использовать функцию клонирования объекта (Clone()), а не создания с нуля. Пропустим здесь описание, где какое бревно располагать, и просто покажем шаги построения стен:



Итак, стены построены. Сейчас у нас есть полностью параметрическая модель основы дома, причем полностью отвечающая физическим требованиям проникновения бревен друг в друга — засчет твердотельных операций с объектами. Это означает, что наша модель дома создается не просто для отображения, а полностью соответствует реально строящемуся дому.
Давайте немного поменяем параметры и посмотрим как это будет изменять дом:


Как видите, имея параметрическую модель, и меняя всего лишь несколько чисел, можно без труда получить бесконечное множество моделей.
Следующим шагом будет добавление в модель окна.
Для построения окна воспользуемся двумя операциями: выдавливания и булевым вычитанием. Конечно, в реальных домах обычно прямоугольные окна, но мы хотим сделать окно какой-нибудь необычной формы, поэтому воспользуемся не просто временным боксом (как можно было бы сделать в случае прямоугольного окна), а выдавим некий закругленный контур.
Итак, сначала создадим такой контур. Он будет состоять из дуги и трех отрезков. Функции создания контура и его выдавливания полностью аналогичны тем, что мы использвали при создании бревна, поэтому не будем на этом заострять внимания. После выдавливания контура окна и расположения его в необходимом месте, получим следующее:

Будем вычитать наше окно из бревен самой первой стены. Поэтому отключим их триангуляцию в функции их создания и триангулируем потом уже результаты применения вычитания окна. Для того, чтобы вычесть из стены окно, необходимо вычесть объект окна из каждого бревна стены. Можно сделать это более оптимально, ведь мы знаем где именно какое бревно расположено и где расположено окно и применять булеву операцию только к тем бревнам, которые дейтсвительно пересекаюся с окном. Но мы будем закладываться на результат булевого вычитания. Если он нулевой — значит объекты не пересекаются. Так же необходимо учесть, что в данном случае результат булевых операций может состоять из нескольких объектов (окно делит бревно на два). Не забываем после все булевых операций удалить временный объект и старые бревна:
size_t oldCnt = m_walls[0].size();
for (int i=0;i<oldCnt;i++)
{
sgCGroup* boolRes = sgBoolean::Sub(*m_walls[0][i], *winObj);
if (boolRes)
{
int ChCnt = boolRes->GetChildrenList()->GetCount();
sgCObject** allChilds = (sgCObject**)malloc(ChCnt*sizeof(sgCObject*));
boolRes->BreakGroup(allChilds);
sgCObject::DeleteObject(boolRes);
sgGetScene()->DetachObject(m_walls[0][i]);
sgDeleteObject(m_walls[0][i]);
for (int j=0;j<ChCnt;j++)
{
((sgC3DObject*)allChilds[j])->Triangulate(SG_VERTEX_TRIANGULATION);
sgGetScene()->AttachObject(allChilds[j]);
}
m_walls[0][i] = (sgC3DObject*)allChilds[0];
for (int j=1;j<ChCnt;j++)
m_walls[0].push_back((sgC3DObject*)allChilds[j]);
free(allChilds);
}
else
m_walls[0][i]->Triangulate(SG_VERTEX_TRIANGULATION);
}
sgDeleteObject(winObj);
После чего получим модель дома с окном:

Остался последний шаг — добавление ската крыши. Это мы сделаем в два этапа — сначала подрежем бревна, которые будут пересекаться в поверхностью крыши, затем создадим саму поверхность ската.
Для начала уберем все вызовы триангуляций всех созданных ранее древен. При создании крыши будет использоваться усечение всех бревен поверхностью крыши — то есть булево вычитание. Триангулируем все результаты этих вычитаний.
Итак, с помощью операции выдавливания, создадим временный объект, который будет усекать наши бревна под поверхность крыши:

И вычтем из всех бревен данный временный объект так же, как вычитали окно из бревен первой стены:

Осталось только создать поверхность ската. Для этого так же воспользуемся операцией выдавливания. После чего получаем готовую модель бревенчатого дома:


А так же бесконечное количество вариаций этой модели, путем варьирования параметров:



Автор: wide






