
Итак, завершился третий квалификационный раунд международного чемпионата программистов Russian Code Cup 2016. Как и в предыдущих двух раундах, участники должны были в течение двух часов решить пять задач. Учитывались как правильность, так и скорость решения. В третьем отборочном раунде за шанс выйти в следующий финал сразились 4379 человек. Но только 200 из них завоевали возможность приблизиться к победе в чемпионате. А теперь по сложившейся традиции разберём задачи раунда.
Задача A. Прямоугольник и квадраты
Условие
Ограничение по времени 2 секунды
Ограничение по памяти 256 мегабайт
Илья зашёл к своему другу Филу и увидел у него удивительной красоты прямоугольник со сторонами А и В. Илья понял, что всю жизнь мечтал о прямоугольнике именно такой площади.
Придя домой, он увидел, что весь дом у него заполнен квадратами C × C. Помогите ему собрать из квадратов C × C прямоугольник, как можно меньше отличающийся по площади от увиденного у Фила прямоугольника. А именно: он хочет, чтобы модуль разности площади прямоугольника Фила и собранного прямоугольника был как можно меньше.
Квадраты можно укладывать параллельно осям координат, без промежутков и наложений. Очевидно, что Илья возьмёт хотя бы один квадрат.
Например, если у Фила прямоугольник имеет размер 4 × 5, а у Ильи есть квадраты 3 × 3, то прямоугольник с наиболее близкой к прямоугольнику Фила площадью, который может собрать Илья, — 3 × 6.
Формат входных данных
Входные данные содержат несколько тестовых наборов. В первой строке задано количество тестов t (1 ≤ t ≤ 10 000).
Каждый тестовый пример описывается одной строкой, содержащей три целых числа A, B и C (1 ≤ A, B, C ≤ 109).
Формат выходных данных
Для каждого теста в отдельной строке выведите ответ на него — площадь прямоугольника, собранного Ильёй из квадратов C × C, как можно меньше отличающегося по площади от увиденного у Фила.
Если существует несколько ответов, выведите любой из них.
Примеры
Входные данные
3
4 5 3
2 3 1
6 4 5
Выходные данные
18
6
25
Решение
При решении этой задачи нужно заметить, что важна лишь разность площадей исходного прямоугольника и собранного, а форма может быть любая. Тогда очевидно, что в качестве ответа подойдёт прямоугольник со сторонами C и nC, где n — натуральное число.
Число n несложно вычислить. Оно равно частному A • B и C2, округлённому либо вверх, либо вниз. Осталось выбрать из этих ответов наиболее выгодный и не забыть учесть, что нужно использовать хотя бы один квадрат C × C.
Задача B. Нули и единицы
Условие
Ограничение по времени 2 секунды
Ограничение по памяти 256 мегабайт
Сегодня Петя не сделал домашнее задание по информатике, поэтому его в качестве наказания вызвали к доске. Учитель написал на доске две строки одинаковой длины, состоящие из 0 и 1, и попросил сделать их равными, используя только одну операцию: разрешается взять два соседних символа любой из строк и инвертировать их, при инвертировании символ 0 становится равным 1, а 1 — 0.
Также, чтобы усложнить задание и ещё больше наказать Петю, учитель попросил сделать это за минимальное количество применений данной операции.
Петя в замешательстве и просит у вас помощи, помогите ему.
Например, пусть учитель написал на доске строки 0101 и 1111. Тогда один из оптимальных способов сделать их равными следующий: сначала инвертируем два центральных символа первой строки, получим строки 0011 и 1111. Теперь инвертируем два первых символа второй строки, получим строки 0011 и 0011. Заметим, что есть и другие способы добиться равных строк за два действия.
Формат входных данных
Входные данные содержат несколько тестовых наборов. В первой строке задано количество тестов t (1 ≤ t ≤ 100).
Каждый из следующих t тестов описывается следующим образом: в первой строке описания теста содержится число n (1 ≤ n ≤ 105) — длина строк, написанных учителем. Во второй и третьей строках описания теста содержатся строки, написанные учителем, — две строки длины n из 0 и 1.
Гарантируется, что сумма чисел n по всем тестам не превосходит 105.
Формат выходных данных
Для каждого теста в отдельной строке выведите ответ на него — минимальное количество применений операций, за которое можно сделать строки равными, или -1, если сделать это невозможно.
Примеры
Входные данные
2
4
0101
1111
3
011
111
Выходные данные
2
-1
Решение
Несложно заметить, что операцию инверсии имеет смысл применять только к одной строке: если после применения инверсий первая и вторая строка совпали, то операции со второй строкой можно отменить и применить их к первой строке, после этого строки всё ещё будут равными. Также заметим, что операции можно применять в любом порядке.
Из этого факта следует простой жадный алгоритм: будем идти по первой строке слева направо и поддерживать её текущее состояние. Если в i-м символе s1[i] ≠ s2[i], тогда следует применить инверсию к символам i, i + 1 первой строки. Если в конце s1[n] ≠ s2[n], то нужной последовательности инверсий не существует и ответ равен -1.
Задача C. Новая трасса
Условие
Ограничение по времени 2 секунды
Ограничение по памяти 256 мегабайт
Проектировщик трасс Гер Кильке получил заказ на новый трек «Формулы-Y». Гер планирует использовать свой любимый способ построения трасс. Он ввёл на плоскости, где будет расположена трасса, систему координат, в которой ось X направлена слева направо, а ось Y направлена снизу вверх, и хочет построить трассу со следующими ограничениями:
- Трасса должна быть незамкнутой ломаной из n отрезков, параллельных осям координат.
- Один из концов ломаной является стартом, а другой — финишем, они должны находиться в разных точках.
- Концы отрезков ломаной должны находиться в точках с целыми положительными координатами, не превышающими 3000.
- Длины всех отрезков должны быть ненулевыми.
- При перемещении вдоль ломаной от старта к финишу угол между направлениями двух подряд идущих отрезков должен составлять 90 градусов по часовой стрелке.
- Конец любого отрезка не может находиться на другом отрезке, помимо предыдущего и следующего в ломаной. В частности, отрезки, которые не являются соседними в ломаной, не могут иметь общих фрагментов ненулевой длины.
Гер собирается составить новую трассу из n отрезков, так, чтобы у неё было ровно k самопересечений. Математики объяснили ему, что это возможно, если 0 ≤ k ≤ n2(n2 – 1)/2, где n2 равно n/2, округлённому вниз. Разумеется, Гер выбрал именно такое значение k. Помогите Геру спроектировать новую трассу.
Формат входных данных
Входные данные содержат несколько тестовых примеров. Первая строка файла содержит одно натуральное число t — число тестов.
Каждая из t следующих строк содержит два натуральных числа: n и k (1 ≤ n ≤ 1000, 0 ≤ k ≤ n2(n2 – 1)/2, где n2 равно n/2, округлённому вниз) — число отрезков в ломаной и число самопересечений.
Сумма n по всем тестам одних входных данных не превосходит 104.
Формат выходных данных
Выходной файл должен содержать ответы для каждого из t тестов.
Каждый ответ должен содержать n + 1 строку, i-я из которых содержит координаты i-й вершины в ломаной. Выводить вершины следует в порядке обхода ломаной от старта к финишу. Координаты должны быть положительными целыми числами, не превышающими 3000.
Гарантируется, что при приведённых ограничениях искомая ломаная существует.
Примеры
Входные данные
2
4 1
3 0
Выходные данные
1 3
3 3
3 1
2 1
2 5
3 9
3 1
1 1
1 4
Решение
Это задача на конструктивное построение примера.
Покажем сначала, как построить пример с максимальным значением k. Начнём с горизонтального отрезка, а затем каждым очередным вертикальным отрезком будем пересекать все предыдущие перпендикулярные ему, кроме того, который идёт непосредственно перед ним. Пример для 14 отрезков показан на рисунке.
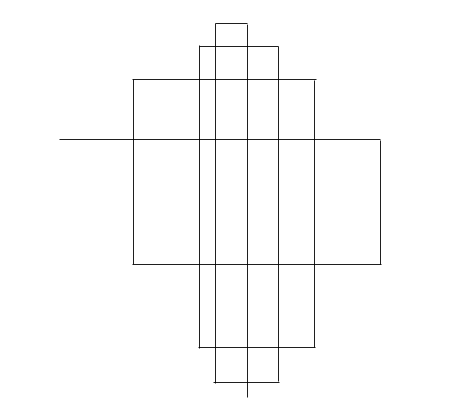
Чтобы получить ровно k, нужно взять 2l отрезков, так, что l(l – 1) ≥ 2k > (l – 1)(l – 2), и построить максимальный пример, правда, возможно, заранее завершив последний отрезок. Оставшиеся же n – 2l отрезков добавим в начало трассы, разместив вокруг по спирали. Пример приведён на рисунке при n = 17 и k = 9.
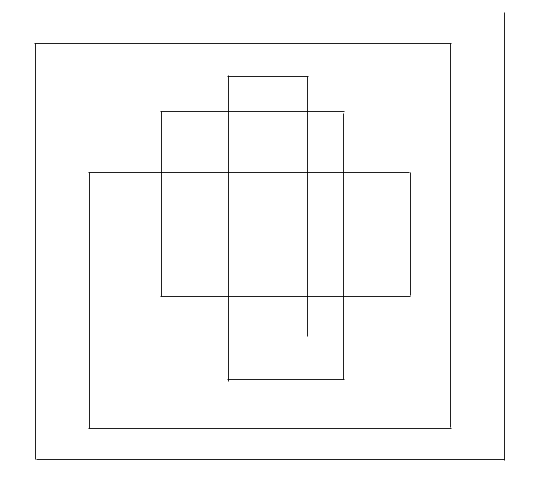
Ограничение на k взято не просто так. Это максимальное число пересечений при фиксированном n. Желающие могут доказать это самостоятельно, подсказка: рассмотрите число пересечений пары отрезков n и n – 1 с парами n – 3 и n – 4, n – 5 и n – 6, ..., 2 и 1 (или просто отрезка 1, если n — чётное).
Задача D. Дерево
Условие
Ограничение по времени 2 секунды
Ограничение по памяти 256 мегабайт
На день рождения Коле подарили подвешенное дерево из n вершин.
Напомним, что подвешенное дерево — это связный неориентированный граф без циклов, в котором одна из вершин является корнем. Родителем вершины называется её сосед, ближайший к корню, у корня нет родителя. Остальные соседи вершины называются её детьми. Вершины подаренного Коле дерева пронумерованы от 1 до n, вершина с номером 1 является его корнем.
Коля решил поиграть со своим деревом. Он выбирает некоторую вершину u, удаляет её и всех её детей подвешивает к её бывшему родителю u. Коля никогда не удаляет корень. Но просто так удалять вершины неинтересно, поэтому он попросил вас иногда находить расстояния между вершинами в текущем графе. Ответьте на все вопросы коварного Коли.
Формат входных данных
В первой строке находится одно целое число n (1 ≤ n ≤ 100 000) — количество вершин в исходном дереве. Во второй строке находятся n – 1 целых чисел pi (1 ≤ pi ≤ n) — номера вершин, которые изначально являются родителями вершин 2, 3, ..., n.
В третьей строке находится одно целое число q (1 ≤ q ≤ 100 000) — количество запросов. В следующих q строках находится описание запросов. Каждый запрос начинается с целого числа, которое равно 1 или 2. Если первое число в запросе равно 1, тогда далее следуют два числа a и b (1 ≤ a, b ≤ n) — две вершины, расстояние между которыми нужно найти. Иначе далее следует одно число v (1 ≤ v ≤ n) — номер вершины, которую нужно удалить.
Гарантируется, что исходное дерево задано корректно, вершины в запросах ранее не были удалены и корень никогда не удаляется.
Формат выходных данных
На каждый запрос второго типа в новой строке выведите расстояние между вершинами.
Примеры
Входные данные
8
1 5 2 1 2 5 5
7
2 4
1 7 6
2 5
1 3 8
1 8 6
2 2
1 8 6
Выходные данные
4
2
3
2
Решение
Сделаем дерево взвешенным и изначально установим у всех рёбер вес 1. Теперь заметим, что если вместо удаления вершины изменять на 0 вес ребра, которое из неё идёт в её родителя, то ответ на запрос на поиск расстояния будет равен расстоянию между вершинами из запроса по взвешенным рёбрам в исходном дереве.
Научимся решать новую задачу, нужно изменять вес ребра в дереве и находить расстояние между вершинами. Для начала в исходном дереве найдём расстояния от корня до всех вершин и выпишем эти расстояния в массив в порядке обхода дерева DFS’ом. Будем при каждом изменении веса ребра поддерживать актуальными эти расстояния. Заметим, что все вершины, расстояние до которых изменится при изменении веса какого-то ребра, соответствуют непрерывному отрезку в массиве. Поэтому, чтобы обработать запрос, нужно прибавить константу на отрезке в этом массиве. Для такой цели, например, можно построить на этом массиве дерево отрезков.
Тогда расстояние между вершинами можно найти так: dab = da + db – 2dlca, где lca — это наименьший общий предок a и b, а dv — это расстояние от корня до v.
Задача E. Варвары
Условие
Ограничение по времени 4 секунды
Ограничение по памяти 256 мегабайт
Оказывается, что жизнь на островах иногда бывает не такой уж приятной! Недавно на страну, территория которой состоит из n островов, напали варвары. Острова этой страны были соединены мостами таким образом, что между двумя любыми островами существовал единственный путь, который не проходит через какой-либо остров дважды.
Варвары понимали, что мосты — слабое место этого государства. Поэтому они начали разрушать их один за другим! Недовольство жителей при этом росло и росло. Изначально недовольство жителей острова i было равно ai.
Рассмотрим, как меняется недовольство жителей некоторого острова x после разрушения очередного моста. Обозначим количество островов, до которых могли добраться жители x до разрушения моста как a, а после разрушения — b. Тогда недовольство возросло в a – b + 1 раз.
Вам предлагается разработать систему для определения текущего недовольства жителей. Вашей программе будут поступать запросы в формате пары чисел u и v. Такой запрос обозначает, что мост, который соединяет города u + res и v + res (где res — ответ на последний запрос), был разрушен. При этом надо считать, что вначале ответ на последний запрос равен 0.
Пусть после разрушения очередного моста недовольство жителей острова i равно bi, тогда нужно сделать res равным остатку от деления суммы всех bi на 109 + 7, а также вывести это значение.
Для лучшего понимания формата входных и выходных данных рассмотрим, что происходит в примере.
Изначально недовольства жителей равны
1 2 3 4 5
После удаления моста между островами 1 и 3 недовольство жителей островов 1 и 2 возросло в 4 раза, а жителей других городов в 3 раза. То есть недовольства после разрушения моста стали равны
4 8 9 12 15
а суммарное недовольство всех равно 48. После этого был разрушен мост между –47 + 48 = 1 и –46 + 48 = 2. Соответственно, недовольства стали равны
8 16 9 12 15
а суммарное недовольство — 60. После этого был разрушен мост, соединяющий острова 3 и 5. Недовольства стали равны
8 16 18 24 45
а суммарное недовольство достигло 111. После разрушения последнего моста недовольства стали равны
8 16 36 48 45
что в сумме составляет 153.
Формат входных данных
В первой строке дано целое число n (2 ≤ n ≤ 2 • 105) — количество островов.
В следующей строке задано n чисел ai (1 ≤ ai ≤ 109 + 6) — начальное недовольство жителей.
В следующих n – 1 строках заданы пары чисел ui, vi (1 ≤ ui, vi ≤ n). Такая пара обозначает, что острова ui и vi соединены мостом. Гарантируется, что от каждого острова до каждого другого можно дойти по мостам ровно одним способом.
В каждой из следующих n – 1 строк даны запросы в формате, который описан в условии. Для лучшего понимания смотрите объяснение к примеру в условии. Гарантируется, что любой мост существовал на момент его разрушения.
Формат выходных данных
Выведите ответ на каждый запрос в отдельной строке.
Примеры
Входные данные
5
1 2 3 4 5
1 2
1 3
3 4
3 5
3 1
-47 -46
-57 -55
-108 -107
Выходные данные
48
60
111
153
Решение
Заметим, что недовольство жителей островов, которые находятся в одной компоненте связности, равно их начальному недовольству, умноженному на некоторую величину, общую для всех этих островов. Будем поддерживать эти значения для всех компонент.
Научимся обрабатывать удаление ребра за время, пропорциональное размеру меньшей компоненты. Тогда суммарное время работы алгоритма будет O(nlogn). Доказать это можно следующим образом. Для некоторой вершины рассмотрим размер компоненты, в которой она находится. Тогда каждый раз, когда она будет рассмотрена, размер этой компоненты уменьшается как минимум в два раза. Заметим, что каждая вершина будет рассмотрена O(logn) раз.
Если при удалении ребра мы будем знать, какая из компонент меньшая, то сможем обойти все её вершины и переместить их в другую компоненту (пересчитав все нужные суммы). Чтобы найти меньшую из компонент, запустим два обхода в ширину в двух компонентах одновременно. А когда один из них посетит все вершины в своей компоненте, не будем продолжать работу второго обхода в ширину. Такой алгоритм работает за время, пропорциональное размеру меньшей из компонент.
***
Чемпионат Russian Code Cup входит в число инициатив Mail.Ru Group, направленных на развитие российской IT-отрасли и объединённых ресурсом IT.Mail.Ru. Платформа IT.Mail.Ru создана для тех, кто увлекается IT и стремится профессионально развиваться в этой сфере. Проект объединяет чемпионаты Russian Ai Cup, Russian Code Cup и Russian Developers Cup, образовательные проекты Технопарк в МГТУ им. Баумана, Техносфера в МГУ им. М. В. Ломоносова и Технотрек в МФТИ. Кроме того, на IT.Mail.Ru можно с помощью тестов проверить свои знания по популярным языкам программирования, узнать важные новости из мира IT, посетить или посмотреть трансляции с профильных мероприятий и лекции на IT-тематику.
Автор: Mail.Ru Group






