Новые производные функций Бесселя выведены с помощью языка Wolfram Language

Почти через двести лет после того, как Бессель ввёл свои одноименные функции, были найдены выражения для их производных по параметрам, справедливые во всей комплексной плоскости

В этом блоге мы приведём и прокомментируем некоторые ранее неизвестные производные специальных функций (в первую очередь функций Бесселя и связанных с ними функций), а также коснёмся истории и текущего состояния дифференцирования по параметрам гипергеометрических и других функций. Одной из основных новых формул (более подробно ниже) является замкнутое выражение для первой производной одной из самых популярных специальных функций — функции Бесселя J:

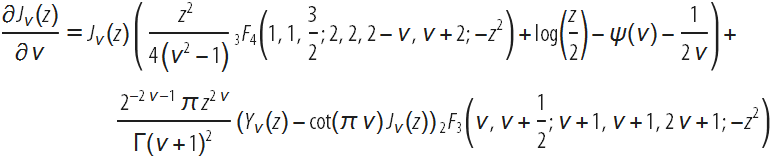
Многие функции математической физики (то есть функции, которые часто используются и поэтому имеют специальные названия) зависят от нескольких переменных. Один из них, как правило, называется аргументом, в то время как другие, как правило, называются параметрами или иногда индексами (значками). Эти специальные функции могут иметь любое количество параметров. Например (см. Wolfram Functions Site), функции Бесселя (z) и (z), Неймана (z), Макдональда (z), и Струве (z) и (z) имеют только один параметр (так называемый индекс), в то время как функции Уиттекера (z) и (z), а также вырожденные гипергеометрические функции (a;b;z) и U(a,b,z) имеют два параметра. Функции Aнгера (z) и (z), а также функции Вебера (z) и (z) могут иметь один или два параметра (в случае двух параметров они называются обобщенными функциями Ангера и Вебера). Функции Аппеля и Гумберта имеют от трех до пяти параметров, в то время как более сложные специальные функции, такие как обобщенная гипергеометрическая функция , могут иметь любое конечное количество параметров.

Среди других свойств, дифференцирование специальных функций играет существенную роль, так как производные характеризуют поведение функций при изменении этих переменных, и они также важны для изучения дифференциальных уравнений этих функций. Как правило, дифференцирование специальной функции по ее аргументу не представляет существенных трудностей. Самая большая коллекция таких производных, включающая первую, вторую, символьную и даже дробного порядка для более чем 200 функций доступна в разделе “Differentiation” (Дифференцирование) на сайте Wolfram Functions (скажем, эта секция включает в себя выражения для 21 производной функции Бесселя (z)), или в книге Ю. А. Брычкова Handbook of Special Functions). Большинство этих формул также доступны непосредственно в языке Wolfram Language. Их можно получить с помощью новых функций MathematicalFunctionData и EntityValue.

Однако производные по параметрам (в отличие от аргумента) в общем случае вычислить гораздо сложнее. Примечательно, что приведённая выше формула, включающая производную первого порядка (относительно параметра ν) одной из наиболее часто встречающихся специальных функций математической физики, лишь недавно была найдена в замкнутом виде, и этот, может быть, удивительный факт говорит о сложности общей задачи. Таким образом, с помощью функции Бесселя J в качестве характерного примера, мы предпримем краткую экскурсию по истории дифференцирования этой специальной функции.

Вычисление производных не всегда просто

Часто люди, даже хорошо знакомые с математическим анализом, склонны думать, что интегрировать трудно, а дифференцировать легко. Известна “народная” мудрость, гласящая, что “дифференцирование — дело техники, а интегрирование — это искусство”. Но это высказывание полностью справедливо только для элементарных функций, для которых дифференцирование приводит снова к элементарным функциям (или их комбинациям). Если же дифференцирование проводится по параметрам, оно, как правило, приводит к сложным функциям более общего класса.

Различие между дифференцированием по параметрам и дифференцированием по аргументу может быть проиллюстрировано на функции Бесселя J. Производная Бесселя J по ее аргументу z была известна в течение достаточно долгого времени и имеет относительно простой замкнутый вид:

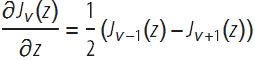
Однако аналитическое вычисление её производной по параметру ν является более сложным. Часто производные по параметрам могут быть записаны в виде интеграла или бесконечного ряда, но эти объекты не могут быть представлены в замкнутой форме через другие простые или известные функций. Исторически сложилось, что некоторые специальные функции были введены с единственной целью — дать простое обозначение для производных известных функций. Например, полигамма-функция возникла как средство для представления производных гамма-функции.

Обобщенная гипергеометрическая функция и её производные играют существенную роль в решении различных задач теоретической и прикладной математики (см., например, статью L. U. Ancarani и G. Gasaneo относительно применения производных по параметрам в квантовой механике). Обобщенная гипергеометрическая функция порождает в качестве частных случаев многие из наиболее часто используемых элементарных функций (например, тригонометрические, гиперболические, логарифмические, и обратные тригонометрические функции), а также многие специальные функции, в том числе функции Бесселя, Струве, Кельвина, Ангера-Вебера, неполную гамма-функцию и интегральные функции (показательную, синус и косинус). В случае, если p=0, q=1, обобщенная гипергеометрическая функция содержит семейство функций Бесселя (z), (z), (z), и (z). Функция Бесселя J, например, имеет следующее гипергеометрическое представление:

Интересно, что история функции (z) начинается почти ровно 200 лет назад. В докладах Берлинской академии за 1816-17 годы (опубликовано в 1819 г.), в работе Analytische Auflösung der Keplerschen Aufgabe, Фридрих Вильгельм Бессель рассматривает так называемое уравнение Кеплера M=E-e sin(E), где M — средняя аномалия, E — эксцентрическая аномалия, а e — эксцентриситет кеплеровской орбиты. Решение этого уравнения может быть представлено (в современной записи) через функции Бесселя целого порядка:

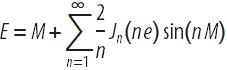
В этой первой работе Бессель ещё не использует современные обозначения, но его функция появляется уже в неявном виде. Например, он использует следующую сумму (обратите внимание, что Бессель использует обозначение Гаусса для i!):

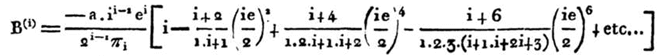
В наше время мы можем записать это выражение в виде суммы двух функций Бесселя на языке Wolfram Language следующим образом:

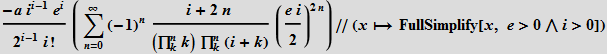
Эта сумма как раз и является первой производной функции Бесселя -2 a e (e i):

В своей следующей работе в 1824 г. Бессель использует почти современные обозначения (замена J I) для обозначения своей функции:

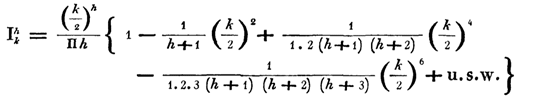
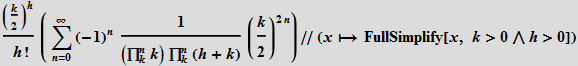
Он также выводит фундаментальные соотношения для этой функции, такие как:

Различные специальные случаи общей функции Бесселя встречаются уже в трудах Бернулли, Эйлера, Даламбера и других (подробнее см. статью). Основным справочником по функциям Бесселя по сей день остается классическая монография Г. Н. Ватсона “Теория бесселевых функций”, которая была многократно переиздана и существенно дополнена по сравнению с первым изданием 1922 г.

Таким образом, в то время как производные функции Бесселя J относительно аргумента z были известны с начала девятнадцатого века, только к середине двадцатого века были найдены частные случаи для производных по индексу. Производные некоторых функций Бесселя по ν в точках ν=0,1,2,… и ν=1/2 были даны Дж. Р. Эйри в 1935 году, а выражения для других функций семейства Бесселя в этих точках — в книге В. Магнуса, Ф. Бейтмена и Р. П. Сони “Формулы и теоремы для специальных функций математической физики“ (1966):

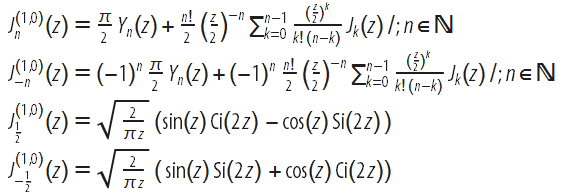
Обобщение на любые полуцелые значения ν было представлено на Международной конференции по абстрактному и прикладному анализу (Ханой, 2002) в следующем виде:

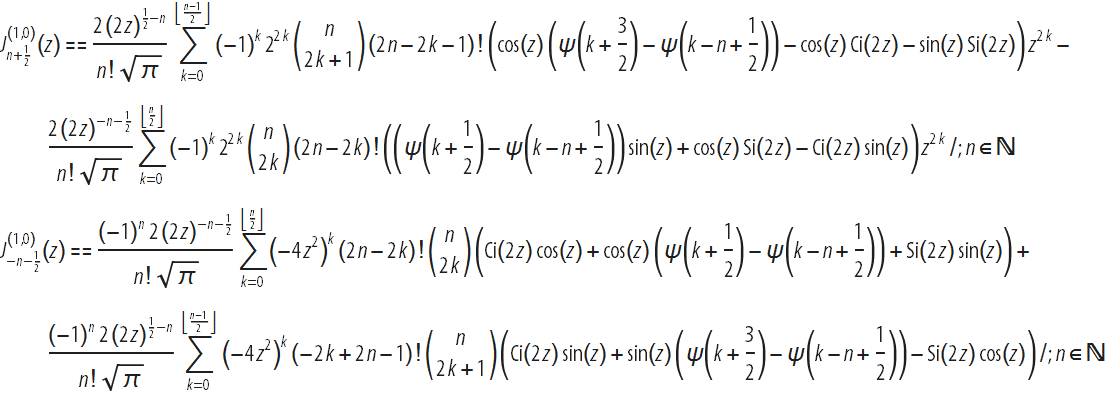
Эти результаты, наряду с выражениями для производных по параметру функций Струве в целых и полуцелых точках, были опубликованы в 2004-2005 гг. Различные новые формулы для дифференцирования по параметрам функций Ангера и Вебера, функций Кельвина, неполных гамма-функций, функции параболического цилиндра, функций Лежандра и Гаусса, обобщенных и вырожденных гипергеометрических функций можно найти в “Справочнике по специальным функциям: Производные, интегралы, ряды и другие формулы”. Краткий обзор и ссылы см. H. Cohl.

Вероятно, покажется удивительным, что при наличии всех этих результатов, первые производные функций Бесселя в замкнутом виде при произвольных значениях параметра были получены только в 2015 г. (Ю. А. Брычков, ”Высшие производные функций Бесселя относительно индекса“, 2016 г.). Они выражаются в виде комбинаций произведений функций Бесселя и обобщенных гипергеометрических функций. Например:

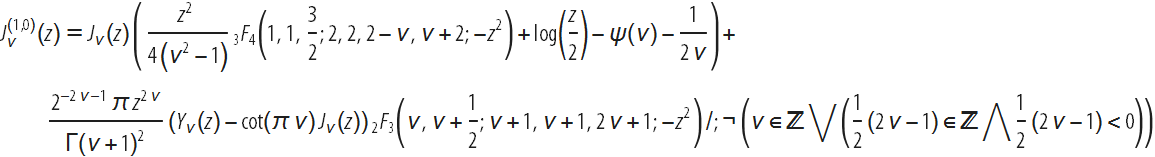
Графики ниже дают некоторое представление о поведении функции Бесселя (z) и ее производной в областях, представляющих интерес. Во-первых, мы приводим (в действительной ν-z-плоскости) выражение для первой производной от (z) по ν (см. уравнение в начале статьи):

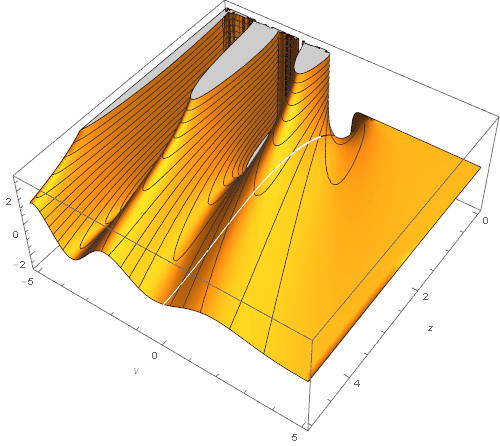
Для фиксированного индекса, а именно ν=π, мы приводим графики функции Бесселя вместе со своими первыми двумя производными (по аргументу и индексу):

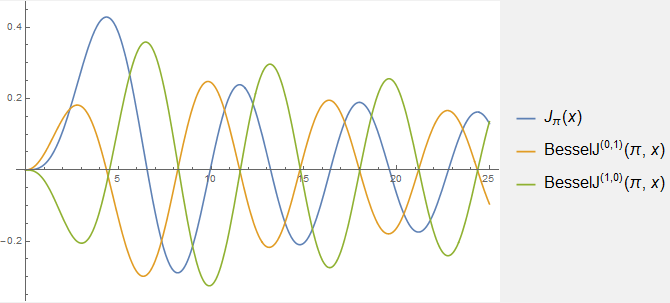
Интересно отметить, что производные (по z и по ν) имеют почти совпадающие нули.

Как мы получили это?

Примечательно, что даже почти через 300 лет после введения классической функции (функция Бесселя (z) была введена Даниилом Бернулли в 1732 г.), по-прежнему можно найти новые и относительно простые формулы, относящиеся к таким функциям. Фактически формулы для введенной выше производной (вместе с соответствующими результатами для производной , и функций Неймана, Макдональда и Кельвина) были получены с помощью языка Wolfram Language. Подробная информация о том, как искались эти производные опубликована здесь. В этом посте мы приведём лишь набросок одного из вариантов подхода, который может быть использован и для других специальных функций.

Во-первых, напомним, что функции Бесселя и другие, которыми мы сейчас интересуемся, являются функциями гипергеометрического типа; но дифференцирование по параметрам общей гипергеометрической функции одной переменной требует более сложных функций гипергеометрического типа более чем одной переменной (см. статью L. U. Ancarani и G. Gasaneo). Первая производная по отношению к “верхним” параметрам , и все производные символьного целого порядка m по отношению к “нижним” параметрам обобщенной гипергеометрической функции, могут быть выражены в терминах гипергеометрической функции Кампе де Ферье двух переменных по следующим формулам:

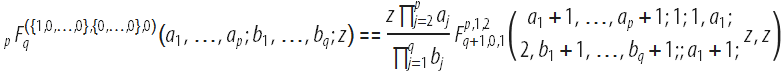
Вышеуказанная гипергеометрическая функция Кампе де Ферье определяется двойным рядом (см. здесь и здесь):

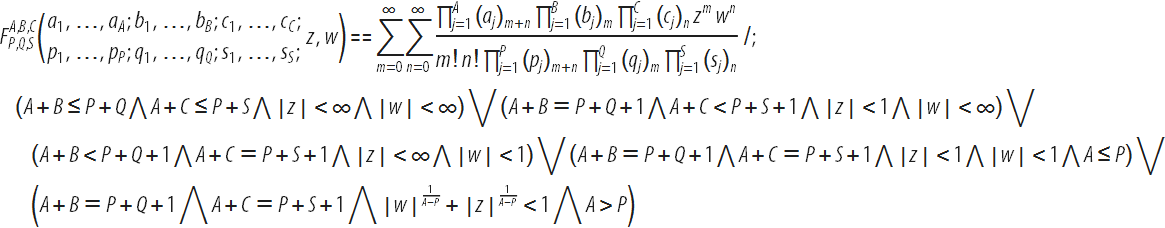
Функцию Кампе де Ферье можно рассматривать как обобщение гипергеометрической функции на две переменные:

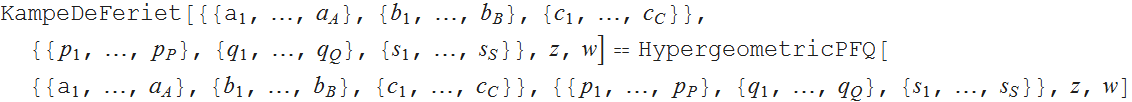
Соответствующая регуляризованная версия функции также может быть определена путем замены произведения символов Похгаммера 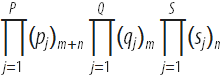в знаменателе на .

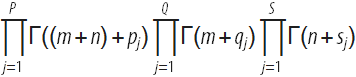Функция Кампе де Ферье может быть использована для представления производных функции Бесселя J по параметру:

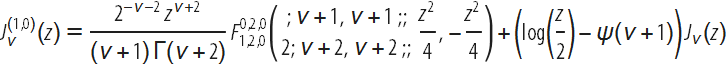
Это выражение совпадает с простой формулой выше, которая включает в себя гипергеометрические функции одной переменной, хотя это сразу не очевидно (мы пока ещё не имеем полного набора формул для упрощения многомерных гипергеометрических функций до выражений, содержащих только одномерные гипергеометрические функции).

Двойные ряды, аналогичные приведенному выше определению обобщенной гипергеометрической функции двух переменных, также возникают при вычислении преобразования Меллина от произведений трех G-функций Мейера:

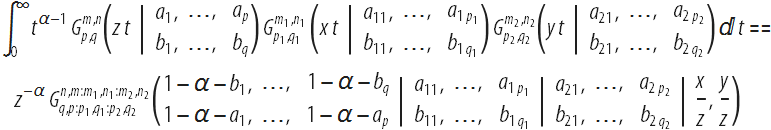
Правая часть этой формулы включает в себя G-функцию Мейера двух переменных, которая в общем (нелогарифмическом) случае может быть представлена в виде конечной суммы гипергеометрических функций Кампе де Ферье с некоторыми коэффициентами, по аналогии с двумя формулами (первая, вторая) для G-функции Мейера одной переменной. Наконец, функция Кампе де Ферье также возникает при разделении действительной и мнимой частей гипергеометрических функций от одной переменной, z = x+iy, с действительными параметрами:

(вышеприведенная формула была выведена Э. Д. Крупниковым, но не опубликована).

Следует отметить, что в последние годы гипергеометрические функции многих переменных находят все большее число приложений в таких областях, как квантовая теории поля, химия, машиностроение, теория связи и радиолокации. Многие практические результаты могут быть представлены с использованием таких функций, и поэтому большинство основных результатов в этой области получены в прикладной научной литературе. Теория таких функций в теоретической математике до сих пор разработана относительно слабо.

Символьные производные в языке Wolfram Language

Автор этих новых и интересных формул с символьными производными, Юрий Брычков, является членом нашей команды, что позволяет нам довести эту постоянно развивающуюся область математики до внимания наших пользователей. Нам также повезло, что в нашем распоряжении имеется новая функция системы Mathematica (языка Wolfram Language) — Entity, которая позволяет, помимо прочего, быстро (в течение нескольких недель или дней) представлять новые результаты в вычисляемом формате и на всех платформах, где используется язык Wolfram Language, нашим пользователям. Например, в системе Mathematica, можно вычислитьследующее выражение:

Тем самым мы получаем основную формулу этой статьи. Мы можем проверить формулу численно, подставив сначала символьные значения ν и z, и получив выражение:

Далее, мы отделяем левую и правую части и подставляем случайные значения для аргумента и параметра:

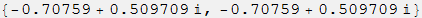
Численная производная от левой части вычисляется в языке Wolfram Language с помощью предельной процедуры. Равенство левой и правой частей, и, следовательно, правильность исходной формулы для производной очевидны.

Помимо множества новых результатов относительно символьных и параметрических производных, которые упоминались в этой статье и доступны только через EntityValue (хотя более глубокая интегрирация этого функционала в будущих версиях языка Wolfram Language требует постоянных усилий), большое количество результатов в этой области уже было имплементировано в ядро системы Mathematica и ядро языка Wolfram Language. Такие производные по параметрам не вычисляются автоматически по причине их сложности, но их можно увидеть, используя команду FunctionExpand. Например:

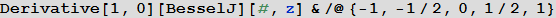
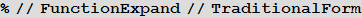
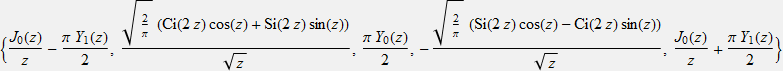
Производные по индексу второго и более высокого порядка функций Бесселя и связанных с ними функций могут быть выражены в терминах гипергеометрической функции Кампе де Ферье двух переменных , но полученные формулы могут быть довольно сложными, и могут включать в себя полиномы Белла Y:

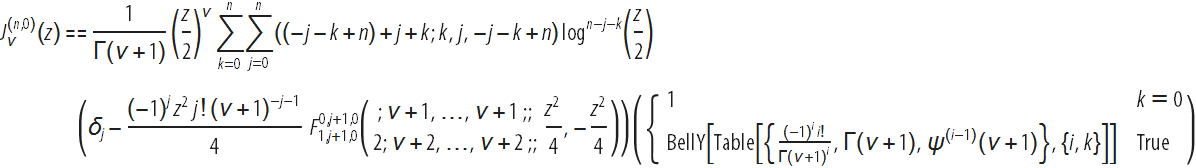
Последнее выражение возникает из представления функции Бесселя (z) через композицию функции (;ν+1;w) и :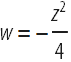

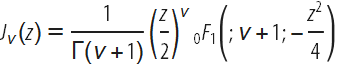
Мы используем формулу Фаа-ди-Бруно, которая позволяет получить выражение n-й производную композиции m функций . В случае m = 2 (см. здесь и здесь), мы получаем, например, выражение:

<img src=«habrastorage.org/getpro/habr/post_images/6a9/62b/4cd/6a962b4cd8ff81622ea203aa642d6921.png» alt=«BesselDerivativesBlogRussian_90.png»">

Соответствующая формула для общих m и n может быть получена и проверена в языке Wolfram Language:

В то время как многочлены Белла Y, для которых не существует общего замкнутого вида, как правило, необходимы для представления производных высшего порядка, один из авторов этого поста, Юрий Брычков, нашел способ устранить многочлены Y из n-х производных по параметру функций Бесселя, оставляя нас с замечательным результатом:

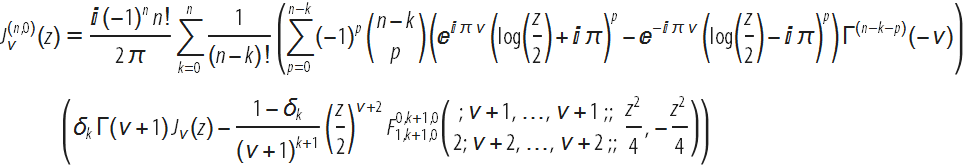
Для удобства заинтересованных пользователей, которые хотели бы видеть в одном месте все известные формулы для производных специальных функций по параметрам (в том числе те, которые перечислены выше), мы собрали и представили эти формулы следующими способами:

1. В табличном формате (скачать здесь).

2. В формате ноутбука Mathematica (скачать здесь).

3. Подмножество формул, которые были известны до 2009, можно увидеть на сайте Wolfram Function Site в разделах “Дифференцирование” различных функций (например, см. эту страницу).

В нашем следующем посте мы дадим выражения замкнутого вида производных для коллекции из более 400 функций с общими правилами для производных символьного и дробного порядка. Мы надеемся, что вам понравится самостоятельно исследовать мир производны специальных функций с помощью языка Wolfram Language!

По вопросам о технологиях Wolfram пишите на info-russia@wolfram.com

Автор: Wolfram Research

Источник