Так сложилось, что последние полгода я активно занимался тестами производительности и мне кажется, что в этой области IT царит абсолютное непонимание происходящего. В наше время, когда рост вычислительных мощностей снизился (vertical scalability), а объем задач растет с прежней скоростью, проблема производительности становится всё острее. Но прежде, чем броситься на борьбу с производительностью, необходимо получить количественную характеристику.
Краткое содержание статьи:
- Простейший тест: способы измерения теста, выбор статистики (квантили, медиана, среднее).
- Параметризованный тест: оценка сложности алгоритма, применения МНК к оценки линейности теста.
- Тесты на многоядерных машинах: сложность экстраполяции результатов тестов на многоядерные машины, закон Амдала и целесообразность измерений.
- Поведенческий тест: каким, при заданной модели поведения пользователей, будет время ожидание запроса и что может привести к коллапсу системы. Пропускная способность (throughput) и как его считать.
- Удивительное статическое распределение результатов performance теста.
Предыстория
Однажды, путешествуя в поезде, я захотел посчитать, каково расстояние между столбами электропередач. Вооружившись обычными часами и оценивая среднюю скорость поезда 80-100км/ч (25 м/с), я засекал время между 2-мя столбами. Как ни странно, этот наивный метод давал очень удручающие результат, вплоть до 1.5-2 кратной разницы. Естественно метод несложно было исправить, что я и сделал, достаточно было засечь 1 минуту и посчитать количество столбов. И не важно, что мгновенная скорость на протяжении минуты может варьироваться и даже не важно посчитаем мы последний столб или минута истечет посередине, потому как измерений вполне достаточно для требуемого результата.
Смысл теста в том, чтобы получить убедительные для себя и для других измерения.
Тесты «на коленке»
Эта история мне напоминает то, что происходит с тестированием производительности в Software Engineering. Достаточно частое явление — запуск 1-2 тестов, построение графиков и получение выводов о scalability система. Даже, если есть возможность применить МНК или узнать стандартную ошибку, это не делается за «ненадобностью.» Особенно интересная ситуация, когда после этих 2 измерений, люди обсуждают насколько быстрая система, как она масштабируется и сравнивают её с другими системами по личным ощущениям.
Конечно, оценить, насколько быстро выполняется команда, не сложно. С другой стороны, быстрее не значит лучше. Системы ПО имеют свыше 10 различных параметров, от hardware на котором они работают до input, которые вводит пользователь в разные моменты времени. И зачастую 2 эквивалентных алгоритма могут давать совершенно разные параметры масштабируемости в разных условиях, что делает выбор совсем не очевидным.
Недоверие к тестам
С другой стороны результаты измерений всегда остаются источником спекуляций и недоверий.
— Вчера мы меряли было X, а сегодня 1.1*X. Кто-то что-то менял? — 10% — это нормально, у нас теперь больше записей в БД.
— При проведении теста был отключен антивирус, скайп, анимация заставки?
— Не-не, для нормальных тестов нам надо закупить кластер серверов, установить микросекундную синхронизацию времени между ними… удалить ОС, запускать в защищенном режиме…
— Сколько пользователей мы поддерживаем? У нас 5000 зарегистрированных пользователей, вдруг 20% из них залогинится, надо запускать тесты с 1000 параллельными агентами.
Что же нам делать?
Во-первых, стоит признать, что железо, которое мы имеем, у нас уже есть и надо получить максимум результатов именно на нём. Другой вопрос, как мы сможем объяснить поведение на других машинах (production/quality testing). Те кто ратует, за эксперименты «чистой комнаты», попросту вам не доверяют, так как вы не даете достаточно объяснений или данных, «чистая комната» — это иллюзия.
Во-вторых, самое главное преимущество в тестировании программ — это дешевизна тестов. Если бы физики могли провести 100 тестов упрощенной ситуации вместо 5 полноценных, они бы точно выбрали 100 (и для проверки результатов 5 полноценных :) ). Ни в коем случае, нельзя лишаться дешевизны тестов, запускайте их у себя, у коллеге, на сервере, утром и в обед. Не поддавайтесь соблазну «реальных» часовых тестов с тысячами пользователей, важнее понимать, как ведет себя система, нежели знать пару абсолютных чисел.
В-третьих, храните результаты. Ценность тестов представляют сами измерения, а не выводы. Выводы гораздо чаще бывают неправильными, чем сами измерения.
Итак, наша задача провести достаточное число тестов, для того, чтобы прогнозировать поведение системы в той или иной ситуации.
Простейший тест
Сразу оговоримся, что мы рассматриваем систему как «черный ящик». Так как системы могут работать под виртуальные машиной, с использованием БД и без, не имеет смысла расчленять систему и брать измерения в середине (обычно это приводит к неучтенным важным моментам). Зато если есть возможность тестировать систему, в разных конфигурация это обязательно следует делать.
Для тестирования, даже простого теста, лучше иметь независимую систему как JMeter, которая может подсчитать результаты, усреднить. Конечно, настройка система требует время, а хочется получить результат гораздо быстрее и мы пишем что-то такое.
long t = - System.currentTimeMillis();
int count = 100;
while (count -- > 0) operation();
long time = (t + System.currentTimeMillis()) / 100;
Запись результата измерения
Запустив один раз мы получаем число X. Запускаем еще раз получаем 1.5*X, 2 *X, 0.7*X. На самом деле тут можно и нужно остановиться, если мы делаем временный замер и нам не надо вставлять это число в отчет. Если же мы хотим поделиться этим числом с кем-то, нам важно, чтобы оно сходилось с другими измерениями и не вызывало подозрений.
Первым «логичным» шагом кажется положить числа X и усреднить их, но, на самом деле, усреднение средних ни что иное, как увеличение count для одного теста. Как ни странно увеличение count может привести к еще более не стабильным результатам, особенно если вы будете запускать тест и делать что-то одновременно.
Минимальное время исполнения как лучшая статистика
Проблема в том, что среднее является не стабильной характеристикой, одного заваленного теста, выполнявшегося в 10 раз дольше, будет достаточно, чтобы ваши результаты не совпадали с другими. Как не парадоксально для простых performance тестов желательно брать минимальное время исполнения . Естественно operation() должна быть измеряемая в данном контектсе, обычно 100 мс — 500 мс для системы более, чем достаточно. Конечно, минимальное время не будет 1 к 1 совпадать с наблюдаемым эффектом или с реальным, но это число будет сравнимо с другими измерениями.
Квантили
Квантили 10%, 50% (медиана), 90% являются более стабильными, чем среднее, и гораздо информативнее. Мы можем узнать с какой вероятностью запрос будет выполняться время 0.5*X или 0.7*X. С ними есть другая проблема, посчитать квантили на коленке гораздо сложнее чем взять min, max.
JMeter предоставляет измерение медианы и 90% в Aggregate Report из коробки, чем естественно следует пользоваться.
Параметризованный тест
В результате измерений мы получаем некоторое число (медиану, минимум или другое), но что мы можем сказать о нашей системе (функции) по одному числу? Представьте вы автоматизируете процесс получения этого числа и каждый день вы будете его проверять, когда вам надо бить тревогу и искать виноватых? К примеру, вот типичный график один и тот же тест каждый день.
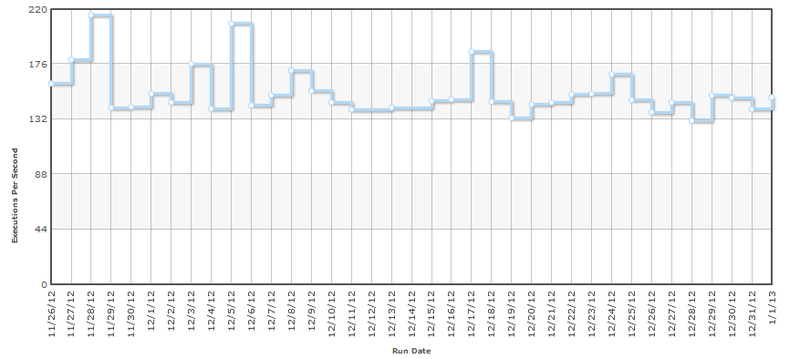
Если мы захотим написать отчет производительности, с одним числом он будет выглядеть пусто. Поэтому мы обязательно протестируем для разных параметров. Тесты для разных параметров дадут нам красивый график и представление о scalability системы.
Тест с одним параметром
Рассмотрим систему с одним числовым параметром. Прежде всего необходимо выбрать значения параметров. Не имеет смысла выбирать числа из разных диапазонов, как [1, 100, 10000], вы попросту проводите 3 абсолютно разных несвязных теста и найти зависимость на таких числах будет невозможно. Представьте вы хотите построить график, какие числа вы бы выбрали? Что-то похожее на [X*1, X * 2, X*3, X*4,X*5, ].
Итак выбираем 5-10 (7 лучшее) контрольных точек, для каждой точки проводим 3-7 измерений, берем минимальное число для каждой точки и строим график.

Сложность алгоритма
Как можно заметить точки располагаются аккурат вокруг мнимой прямой линии. Теперь мы подходим к самой интересной части измерений, мы можем определить сложность алгоритма исходя из измерений. Определение сложности алгоритма на основании тестов гораздо проще для сложных программ, чем анализ текста исходных программ. При помощи теста можно даже найти специальные точки, когда сложность меняется, например, запуск Full GC.
Определение сложности программы по результатам теста является прямой задачей Регрессионного анализа. Очевидно, что не существует общего способа нахождения функции только по точка, поэтому для начала делается предположение о некоторой зависимости, а затем оно проверяется. В нашем случае и в большинстве других, мы предполагаем что функцией является линейная зависимость.
Метод наименьших квадратов (линейная модель)
Для поиска коэффициентов линейной зависимости имеется простой и оптимальный метод МНК. Преимущество этого метода в том, что формулы можно запрограммировать в 10 строчек и они абсолютно понятны.
y = a + bx
a = ([xy] - b[x])/[x^2]
b = ([y] - a[x])/ n
Представим наши вычисления в таблице.
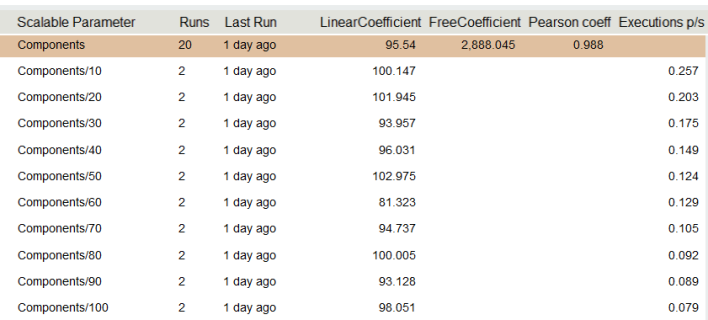
В выделенная строчке мы видим линейный коэффициент нашей модели, он равняется 95.54, свободный коэффициент 2688. Теперь мы можем проделать простой, но не очевидный фокус, мы можем придать значение этим числам. 95.54 измеряется в миллисекундах (как и наши измерения), 95.54 — время которое мы тратим, на каждую компоненту, а 2688 мс время, которое мы тратим на саму систему, не зависит от количества компонент. Данный метод позволил нам выделить достаточно точно время внешней системы, в данном случае БД, хотя оно в десятки раз превышает время 1-й компоненты. Если бы мы пользовались формулой Time_with_N_component/N нам бы пришлось замерять для N>1000, чтобы погрешность оказалась меньше 10%.
Линейный коэффициент модели является самым важным числом нашего измерения и как ни странно он является самым стабильным числом наших измерений. Так же линейный коэффициент позволяет адекватно измерить и интерпретировать операции, которые происходят за наносекунды, причем отделив overhead самой системы.
На графике результаты независимых запусков теста в разное время, что подтверждает большую стабильность линейного коэффициента, чем отдельно взятых тестов.
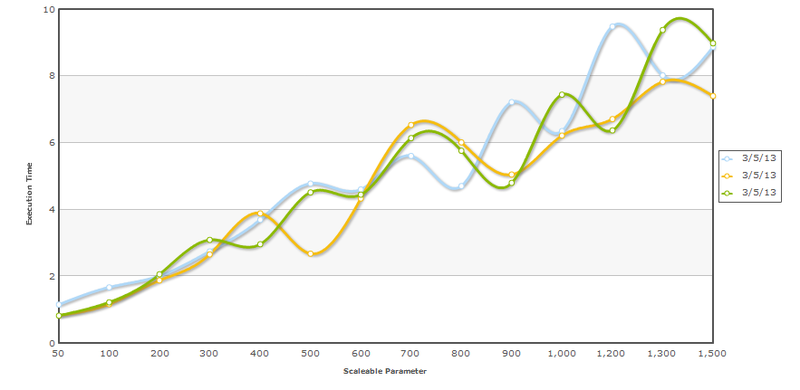
Оценка линейности модели и коэффициент Пирсона
Используя график мы можем наглядно увидеть, что наши измерения действительно удовлетворяют линейной модели, но этот метод далеко не точный и мы не можем его автоматизировать. В этом случае нам может помочь коэффициент Пирсона. Этот метод действительно показывает отклонения от прямой линии, но для 5-10 измерений его явно недостаточно. Ниже приведен пример, явно не линейной зависимости, но коэффициент Пирсона достаточно высок.
Возвращаясь к нашей таблице, зная ovehead системы (свободный коэффициент) мы можем посчитать линейный коэффициент для каждого измерения, что в таблице и сделано. Как мы видим числа (100, 101, 93, 96, 102, 81, 94, 100, 93, 98) — достаточно случайно распределены около 95, что и дает нам весомые основания полагать, что зависимость линейная. Следуя букве математике, на самом деле отклонения от средней величины должны удовлетворять нормальному распределения, а для проверки нормального распределения достаточно проверить критерий Колмогорова-Смирнова, но это мы оставим для искушенных тестировщиков.
Как это ни странно, не все зависимости являются линейными. Первое, что приходит на ум, это квадратичная зависимость. На самом деле квадратичная зависимость очень опасна, она убивает performance сначала медленно, а затем очень быстро. Даже если у вас для 1000 элементов все выполняется за доли секунды, то для 10000 это уже будут десятки секунд (умножается на 100). Другим примером, является сортировка, которая не может быть решена за линейное время. Посчитаем насколько применим метод линейной анализа для алгоритмов со сложность O(n*log n)
(10n log 10n )/ (n log n)= 10 + (10*log 10)/(log n)
То есть для n >= 1000, отклонение будет в пределах 10%, что существенно, но в некоторых случаях может применяться, особенно если коэффициент при log достаточно большой.
Рассмотрим пример нелинейной зависимости.
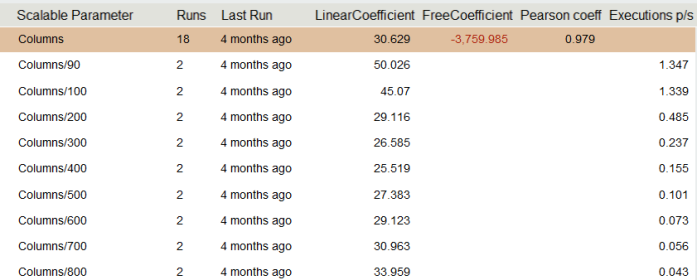
Первое, что следует отметить, отрицательный overhead, по очевидным причинам система не может иметь отрицательное время затрачиваемое на подготовку. Второе, глядя на колонку коэффициентов, можно заметить закономерность, линейный коэффициент падает, а затем растет. Это напоминает график параболы.
Тест с двумя и большим числом параметров
Естественно, что большинство систем не состоят из одного параметра. К примеру, программа чтения из таблицы уже состоит из 2-х параметров, колонок и строк. Используя параметризованные тесты, мы можем посчитать каковы затраты на чтение строки из 100 колонок (пусть 100мс) и каковы затраты на чтение колонки для 100 строк (пусть 150мс). 100*100мс != 100*150мс и это не парадокс, просто мы не учитываем, что в скорости чтения строк уже заложен overhead чтения 100 колонок. То есть 100мс/100 колонок= 1мс — это не скорость чтения одной ячейки! На самом деле 2-х измерений будет недостаточно для расчета скорости чтения одной ячейки. Общая формула такова, где A — затраты на одну ячейку, B — на одну строчку, C — на колонку:
Time(row, column) = A * row * column + B * row + C * column + Overhead
Составим систему уравнений, учитывая имеющиеся значения и еще одно необходимое измерение:
Time(row, 100) = 100 * A * row + B * row + o = 100 * row + o.
Time(row, 50) = 50 * A * row + B * row + o = 60 * row + o.
Time(100, column) = 100 * B * column + C * column + o = 150 * column + o.
100 * A + B = 100.
50 * A + B = 55.
100 * B + C = 150.
Отсюда, получаем A = 0.9 мс, B = 10 мс, C = 50 мс.
Конечно, имея формулу на подобие ЛМНК для данного случая, все расчеты бы упростились и автоматизировались. В общем случае, к нам не применим общий ЛМНК, потому как функция, которая линейная по каждому из аргументов, отнюдь не многомерная линейная функция (гиперплоскость в N-1 пространстве). Возможно воспользоваться градиентным методом нахождения коэффициентов, но это уже не будет аналитический способ.
Многопользовательские тесты и тесты многоядерных систем
Миф «throughput per core»
Одним из любимых занятий с performance тестами является экстраполяция. Особенно люди любят экстраполировать в ту область, для которых они не могут получить значений. К примеру, имея в системе 2 ядра или 1 ядро, хочется проэкстраполировать как бы система вела себя с 10 ядрами. И конечно же первое неверное допущение в том, что зависимость линейна. Для нормального определения линейной зависимости необходимо от 5 точек, что конечно же невозможно получить на 2х ядрах.
Закон Амдала
Одним из самых близких приближений является закон Амдала.
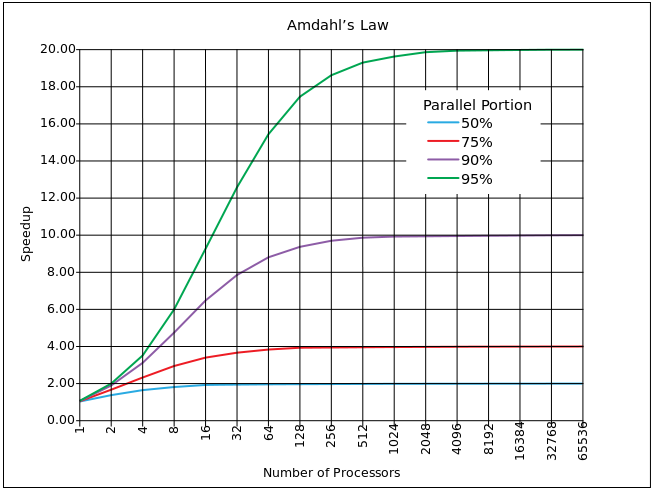
Он основан на расчете процента паралеллизируемого кода α ( вне блока синхронизации) и синхронизируемоего кода (1 — α). Если один процесс занимает время T на одном ядре, тогда при множественных запущенных задачах N время будет T' = T*α + (1-α)*N*T. В среднем конечно же N/2, но Amdahl допускает N. Параллельное ускорение соответственно S = N*T/T' = N / (α + (1-α)*N)=1 / (α/N + (1- α)).
Конечно же, приведенный выше график, не настолько драматичен в реальности (там ведь логарифмическая шкала по X). Однако существенным недостатком блоков синхронизации, является асимптота. Условно говоря, не возможно наращивая мощность преодолеть предел ускорения lim S= 1 / (1- α). И этот предел достаточно жесткий, то есть для 10% синхронизированного кода, предел 10, для 5% (что очень хорошо) предел 20.
Функция имеет предел, но она постоянно растет, из этого возникает, странная на первый взгляд, задача: оценить какое hardware оптимально для нашего алгоритма. В реальности увеличить процент параллизированного бывает достаточно сложно. Вернемся к формуле T' = T*α + (1-α)*N*T, оптимальным с точки зрения эффективности: если ядро будет простаивать, столько же времени сколько и будет работать. То есть T*α=(1-α)*N*T, отсюда получаем N =
α/(1-α). Для 10% — 9 ядер, для 5% — 19 ядер.
Связь количества пользователей и количества ядер. Идеальный график.
Модель ускорения вычислений является теоретически возможной, но не всегда реальной. Рассмотрим ситуацию клиент-сервер, когда N клиентов постоянно запускают некоторую задачу на сервере, одной за одной, и мы не испытываем никаких затрат на синхронизацию результатов, так как клиенты полностью не зависимы! Ведение статистики к примеру вводит элемент синхронизации. Имея M-ядерную машину, мы ожидаем, что среднее время запроса T когда N < M одинаково, а когда N > M время запроса растет пропорционально количеству ядер и пользователей. Посчитаем throughput как количество запросов обрабатываемых в секунду и получим следующие «идеальный» график.
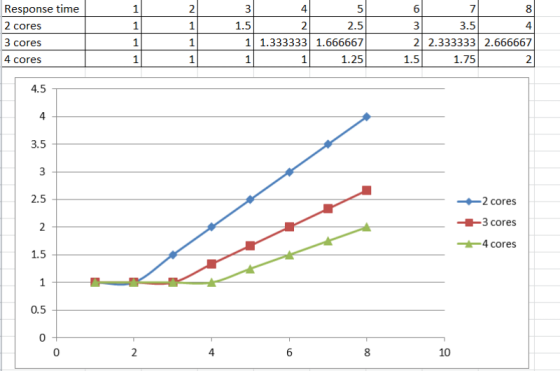
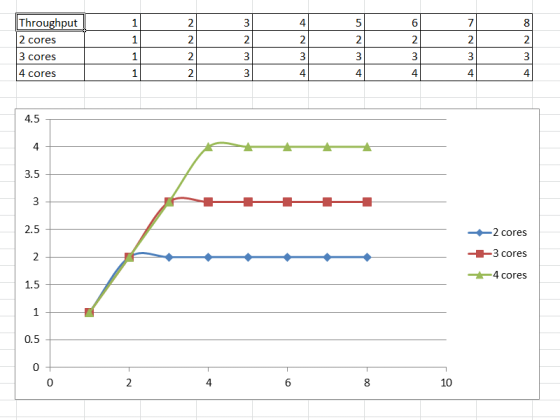
Экспериментальные измерения
Естественно идеальные графики достижимы, если мы имеем 0% synchronized блоков (критических секций). Ниже приведены реальные измерения одного алгоритма с разными значения параметра.

Мы можем рассчитать линейный коэффициент и построить график. Так же имея машину с 8 ядрами, можно провести серию экспериментов для 2, 4, 8 ядер. Из результатов тестов можно заметить, что система с 4 ядрами и 4 пользователями ведет себя точно так же как система с 8 ядрами и 4 пользователям. Конечно, это было ожидаемо, и дает нам возможность проводить только одну серию тестов для машины с максимальным количеством ядер.
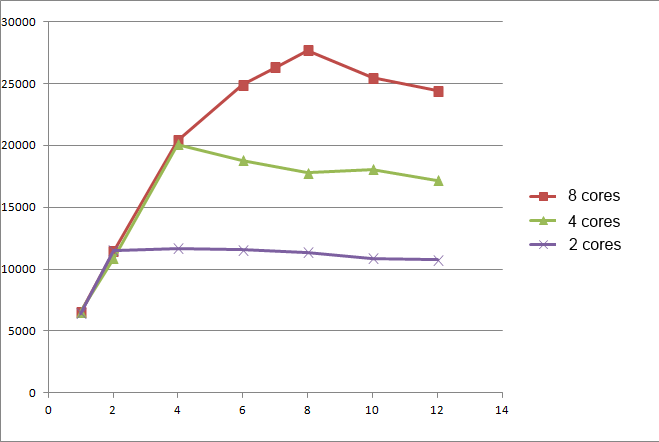
Графики измерений близки по значениям к закону Амдала, но все-таки существенно отличается. Имея измерения для 1, 2, 4, 8 ядер, можно рассчитать количество непараллезируемоего кода по формуле
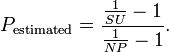
Где NP — количество ядер, SU = Throughpt NP core / Throughput 1 core. Согласно закону Амдала это число должно быть постоянным, но во всех измерениях это число падает, хотя и не значительно (91% — 85%).
График throughput per core не всегда представляет собой непрерывную линию. К примеру, при нехватке памяти или при работе GC отклонения в throughput могут быть очень значительными.
Поведенческий тест
Throughput
При измерениях нагрузки многопользовательских систем мы ввели определение Throughput = NumberOfConcurrentUsers / AverageTimeResponse. Для интерпретации результатов Throughput — это пропускная способность системы, какое количество пользователей система может обслужить в момент времени, и это определение тесно связано с теорией массового обслуживания. Сложность измерения throughput заключается в том, что значение зависит от входного потока. К примеру, в системах массового обслуживания, предполагается, что время ожидания ответа не зависит от того, сколько заявок находится в очереди. В простой программной реализации, без очереди заявок, время между всеми потоками будет делиться и соответственно система будет деградировать. Важно заметить, что не стоит доверять JMeter измерениям throughput, было замечено, что Jmeter усредняет throughput между всеми шагами теста, что является не правильным.
Рассмотрим, следующий случай: при нагрузке с 1 пользователем, система выдает Throughput = 10, при 2-х — Throughput=5. Такая ситуация вполне возможна, так как типичный график Throughput/User — эта функция которая имеет один локальный (и глобальный максимум).
Следовательно, при входящем потоке 1 пользователь каждые 125мс, система будет обрабатывать 8 пользователей в секунду (входной throughput).
При входящем потоке 2 пользователя каждые 125мс система начнет коллапсировать, так как 8 (входной throughput) > 5 (возможного throughput).
Коллапсирующая система
Рассмотрим пример коллапсирующей системы подробнее. После проведения теста Throughput/Users у нас есть следующие результаты.
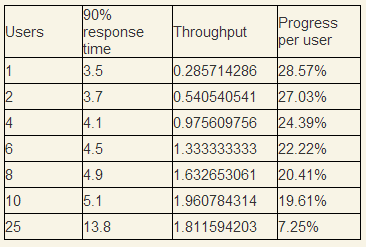
Users — количество пользователей одновременных в системе, Progress per user — какое количество работы в процентах пользователь выполняет за одну секунду. Мысленно сэмулируем ситуацию, что каждую секунду приходит 10 пользователей и начинают выполнять одну и ту же операцию, вопрос, сможет ли система обслуживать данный поток.
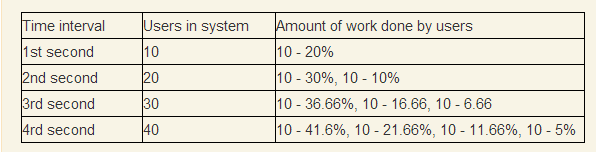
За 1 секунду 10 пользователей в среднем выполнят только 20% своей работы, исходя из предположения, что в среднем они выполняют всю за 5. На 2-й секунде в системе уже будет 20 пользователей и они будут разделять ресурсы между 20 потоками, что еще уменьшит процент выполняемой работы. Продолжим ряд до того, момент когда первые 10 пользователей закончат работу (теоретически они ее должны закончить так как ряд 1/2 + 1/3 + 1/4… расходящийся).
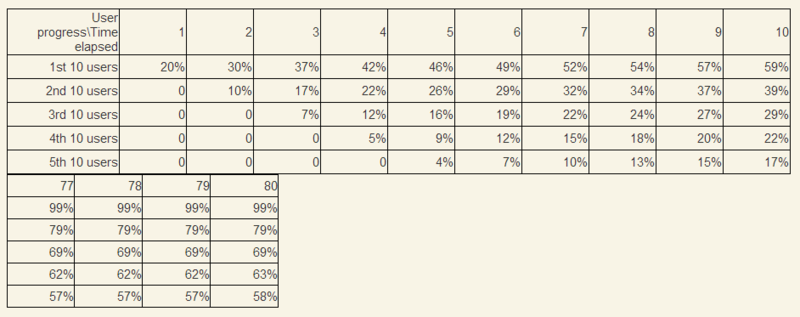
Достаточно очевидно, что система сколлапсирует, так как через 80 секунд в системе будет 800 пользователей, а в этом момент смогут закончить только первые 10 пользователей.
Данный тест показывает, что при любом распределении входящего потока, если входящий throughput (математическое ожидание) больше максимального
измеряемого throughput для системы, система начнет деградировать и при постоянной нагрузке упадет. Но обратное неверно, в 1-м примере максимальный измеряемый throughput (=10) > входящего (8), но система также не сможет справиться.
Система в стационарном режиме
Интересным случаем является работоспособная система. Взяв за основу наши измерения, проведем тест, что каждые 1 секунду приходят 2 новых пользователя. Так как минимальное время ответа превышает секунду, то поначалу количество пользователей будет накапливаться.
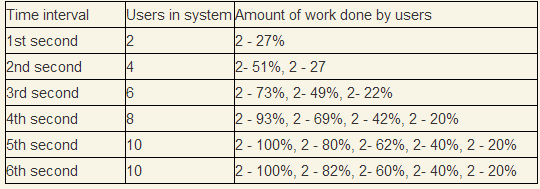
Как мы видим система войдет в стационарный режим именно в той точке, графика когда измеряемый throughput совпадает с входным throughput. Количество пользователей в системе в среднем будет 10.
Из этого можно сделать вывод, что график Throughput/Users с одной стороны представляет количество обрабатываемых пользователей в секунду (throughput) и количество пользователей в системе (users). Падения графика справа от этой точки характеризует только стабильность системы в стрессовых ситуациях и зависимость от характера входящего распределения. В любом случае, проводя тесты Throughput/Users, будет совсем не лишним провести behavioral test с приблизительным характеристиками.
Удивительное распределение
При проведении тестов производительности практически всегда есть измерения занимающие гораздо больше времени, чем ожидалось. Если время тестирования достаточно велико, то можно наблюдать следующую картину. Как из этих всех измерений выбрать одно число?
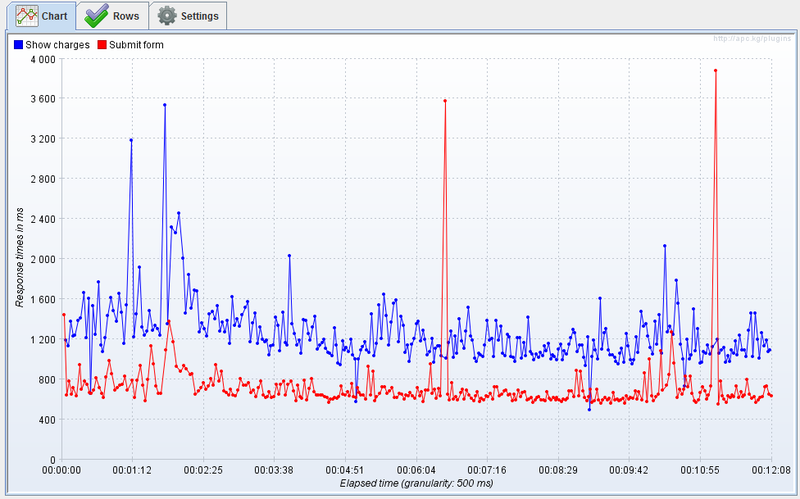
Выбор статистики
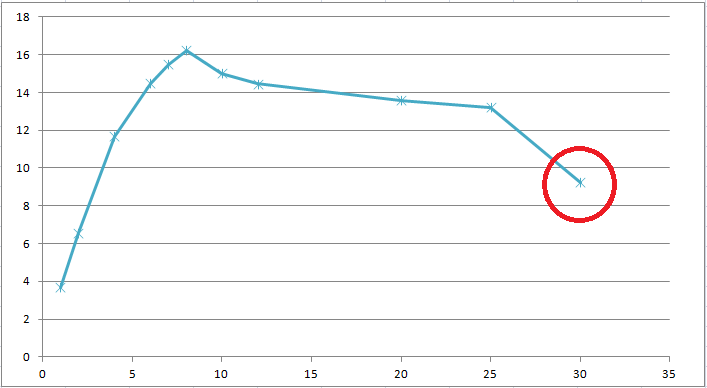
Самой простой статистикой является среднее, но по указанным выше причинам она не совсем стабильна, особенно для малого количества измерений. Для определения квантилей удобно воспользоваться графиком функции распределения. Благодаря замечательному JMeter плагину у нас есть такая возможность. После первых 10-15 измерений обычно картина недостаточно ясная, поэтому для детального изучения функции потребуется от 100 измерений.
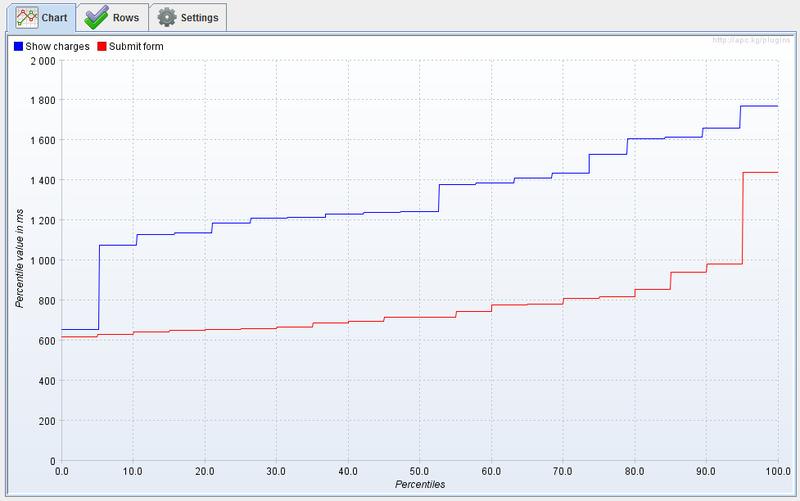

Получить N-квантиль из данного графика очень просто, достаточно взять значение функции в данной точки. Функция показывает достаточно странно поведение вокруг минимума, но дальше растет вполне стабильно и только возле 95% квантиля начинается резкий подъем.
Распределение?
Является ли данное распределение аналитическим или известным? Для этого можно построить график плотности распределения и попытаться посмотреть известные функции, к счастью их не так много.
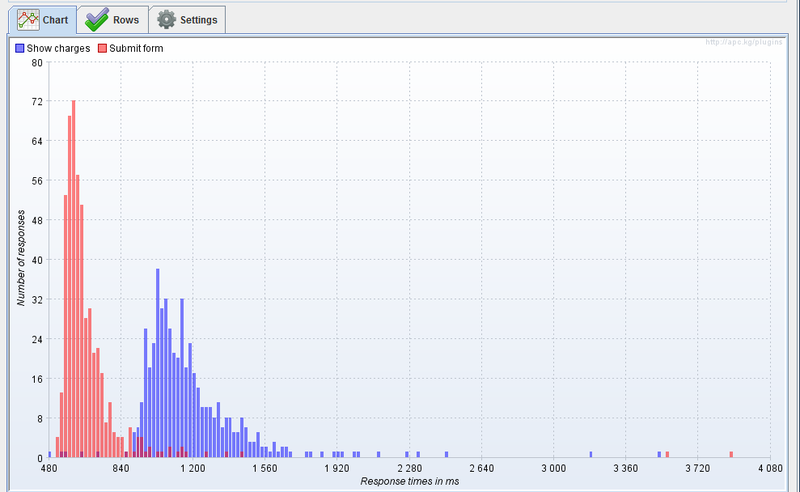
Честно говоря этот метод не принес никаких результатов, на первый взгляд похожие функции распределения: Бета распределение, распределение Максквелла, оказались достаточно далеки от статистик.
Минимум и экспоненциальное распределение
Важно отметить, что область значений нашей случайной величины отнюдь не [0, +∞ [, а некоторое [Min, +∞[. Мы не можем ожидать, что программа может выполниться быстрее, чем теоретический минимум. Если предположить, что измеряемый минимум сходится к теоретическому и вычесть это число из всех статистик, то можно наблютать достаточно интересную закономерность.
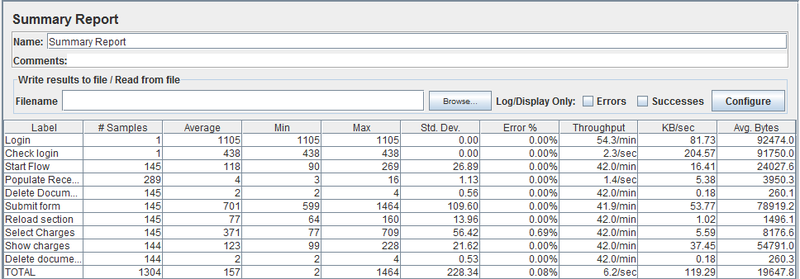
Оказывается Minimum + StdDev = Mean (Average), причем это характерно для всех измерений. Есть одно известное распределение у которого, математические ожидание совпадает с дисперсией (variance), это экспоненциальное распределение. Хотя график плотности распределения отличается в начале области определения, основные квантили вполне совпадают. Вполне возможно случайная величина является суммой экспоненциального распределения и нормального, что вполне объясняет колебания вокруг точки теоретического минимума.
Дисперсия и среднее
К сожалению, мне не удалось найти теоретического обоснования, почему результаты тестов удовлетворяют экспоненциальному распределению. Чаще всего экспоненциальное распределение фигурирует в задачах времени отказа устройств и даже времени жизни человека. Неясно так же, является ли это спецификой платформы (Windows) или Java GC или каких-то физических процессов, происходящих в компьютере.
Однако, учитывая, что каждое экспоненциальное распределение задается 2 параметрами (дисперсией и математическим ожиданием) и функция распределения performance test экспоненциальная, можно считать, что для peformance теста, нам необходимо и достаточно только 2 показателей. Среднее — время выполнения теста, дисперсия — отклонение от этого времени. Естественно, чем меньше дисперсия, тем лучше, но однозначно сказать, что лучше уменьшить среднее или дисперсию, нельзя.
Если у кого-то есть теория, откуда берется дисперсия и как влияет тот или иной алгоритм на ее значение, прошу поделиться. От себя хочу заметить, что зависимости между временем выполнения теста и дисперсии, я не нашел. 2 теста выполняющиеся в среднем одинаковое время (без sleep), могут иметь разные порядки дисперсии.
Автор: vics001