
Данная публикация является переводом второй части статьи Characterization and Optimization Methodology Applied to Stencil Computations инженеров компании Intel. В предыдущей части была описана методология для оценки максимальной производительности, которая может быть получена при использовании какого-либо алгоритма на конкретной платформе на примере довольно распространенного вычислительного ядра, используемого при решении 3D акустического изотропного волнового уравнения. Эта часть описывает серию шагов по оптимизации исходного кода для получения производительности, близкой к ожидаемой отметке.
В следующей части будет рассказано о генетическом алгоритме автотюнинга, который позволяет увеличить производительность реализации за счет подбора наиболее оптимальных параметров запуска и компиляции.
Стандартные оптимизации
Стандартные оптимизации — оптимизации, направленные на улучшение параллелизма, векторизации и локальности данных. Эти 3 области отражают наиболее важные аспекты для оптимизации на современных многоядерных архитектурах. Мы реализовали шаг за шагом следующее:
dev00: Стандартная реализация решения 3D акустического изотропного волнового уравнения для валидации результатов.
dev01: dev00 реализация имела условный переход во внутреннем цикле, чтобы избежать ошибок доступа к данным на границах области. Начиная с AVX, такие переходы реализуются с помощью масок (маскированные инструкции, такие как VMASKMOVPD — прим. переводчика). Таким образом изменения границ циклов реально не повлияло на производительность на 2S-E5, в то время как на Xeon Phi было получено 2-кратное ускорение (рисунок 7).
dev02: Cache blocking снижает количество промахов в кэш и требует только 3 новых цикла (рисунок 1). Недостатком данной оптимизации является добавление 3 новых параметра для контроля размеров блока.
for(int bz=HALF_LENGTH; bz<n3; bz+=n3_Tblock)
for(int by=HALF_LENGTH; by<n2; by+=n2_Tblock)
for(int bx=HALF_LENGTH; bx<n1; bx+=n1_Tblock) {
int izEnd = MIN(bz+n3_Tblock, n3);
int iyEnd = MIN(by+n2_Tblock, n2);
int ixEnd = MIN(n1_Tblock, n1-bx);
int ix;
for(int iz=bz; iz<izEnd; iz++) {
for(int iy=by; iy<iyEnd; iy++) {
float* next = ptr_next_base + iz*n1n2 + iy*n1 + bx;
float* prev = ptr_prev_base + iz*n1n2 + iy*n1 + bx;
float* vel = ptr_vel_base + iz*n1n2 + iy*n1 + bx;
for(int ix=0; ix<ixEnd; ix++) {
float value = 0.0;
value += prev[ix]*coeff[0];
for(int ir=1; ir<=HALF_LENGTH; ir++) {
value += coeff[ir] * (prev[ix + ir] + prev[ix - ir])
;
value += coeff[ir] * (prev[ix + ir*n1] + prev[ix -
ir*n1]);
value += coeff[ir] * (prev[ix + ir*n1n2] + prev[ix -
ir*n1n2]);
}
next[ix] = 2.0f* prev[ix] - next[ix] + value*vel[ix];
}
}}}
Рисунок 1. Исходный код вычислительного ядра с cache blocking.
dev03: Чтобы гарантировать, что переменные являются private для каждого потока не только на каждой отдельной итерации мы разделили #pragma omp parallel и the #pragma omp for директивы, соответствующим образом декларируя private переменные между двумя OpenMP модификаторами (clause).
dev04: #pragma ivdep директива может быть использована для подсказки векторизатору, что элементы массива внутри цикла не пересекаются (т.е. нет так называемого pointer aliasing, что часто предполагаются по умолчанию для C/C++ компилятора). Использование векторизации в этом случае может быть также облегчено при помощи специальных ключей компиляции (-fno-alias) или с помощью C/C++ прагм или директив языка Fortran.
dev05: Даже если компилятор сообщает о векторизованных циклах, использование расширения набора инструкций AVX (а также использование ymm векторных регистров) может быть неэффективно. Соответственно, ручная развертка циклов вместе с такими директивами, как __assume_aligned (для сообщения компилятору, что массивы выровнены — прим. переводчика) может улучшить автоматическую AVX векторизацию (рисунок 2).
__assume_aligned(ptr_next, CACHELINE_BYTES);
__assume_aligned(ptr_prev, CACHELINE_BYTES);
__assume_aligned(ptr_vel, CACHELINE_BYTES);
#pragma ivdep
for(int ix=0; ix<ixEnd; ix++) {
v = prev[ix]*c0
+ c1 * FINITE_ADD(ix, 1)
+ c1 * FINITE_ADD(ix, vertical_1)
+ c1 * FINITE_ADD(ix, front_1)
+ c2 * FINITE_ADD(ix, 2)
+ c2 * FINITE_ADD(ix, vertical_2)
+ c2 * FINITE_ADD(ix, front_2)
+ c3 * FINITE_ADD(ix, 3)
+ c3 * FINITE_ADD(ix, vertical_3)
+ c3 * FINITE_ADD(ix, front_3)
+ c4 * FINITE_ADD(ix, 4)
+ c4 * FINITE_ADD(ix, vertical_4)
+ c4 * FINITE_ADD(ix, front_4)
+ c5 * FINITE_ADD(ix, 5)
+ c5 * FINITE_ADD(ix, vertical_5)
+ c5 * FINITE_ADD(ix, front_5)
+ c6 * FINITE_ADD(ix, 6)
+ c6 * FINITE_ADD(ix, vertical_6)
+ c6 * FINITE_ADD(ix, front_6)
+ c7 * FINITE_ADD(ix, 7)
+ c7 * FINITE_ADD(ix, vertical_7)
+ c7 * FINITE_ADD(ix, front_7)
+ c8 * FINITE_ADD(ix, 8)
+ c8 * FINITE_ADD(ix, vertical_8)
+ c8 * FINITE_ADD(ix, front_8)
next[ix] = 2.0f* prev[ix] - next[ix] + v*vel[ix];
}
Рисунок 2. Исходный код вычислительного ядра с оптимизациями dev04 и dev05. Здесь FINITE_ADD – макрос для симметричной конечной разности (FD) типа v[ix+off]+v[ix-off].
dev06: Факторизация FD коэффициентов (c1, c2, ...) позволяет убрать 2 операции умножения для каждого из коэффициентов. На 2S-E5, данное изменение может уменьшить производительность ввиду увеличения дисбаланса умножений и сложений. Однако, на Xeon Phi in-order микроархитектуре, удаление «лишних» инструкций имеет прямое влияние на возросшую производительность, как отмечено на рисунке 7.
dev07: Непоследовательный доступ в память является известным эффектом на многосокетных платформах. На текущей операционной системе, типичное выделение памяти (например, с помощью mm_malloc) резервирует количество пространства, которое будет необходимо, но физически память выделяется при первом записи/чтении в переменную. Это правило (так называемое first touch policy) вместе с закреплением потоков (well-defined thread или process affinitization), дает возможность разработчикам физически выделить страницы памяти на том же самом NUMA узле, на котором поток будет использовать эти страницы памяти в дальнейшем при вычислениях. Это достигается путем размещения данных при первой инициализации внутри параллельного региона, где в дальнейшем они будут использованы для расчетов.
dev08: Для оптимального использование регистров, данная реализация использует возможности C/C++ по поддержке интринсиков, специфичных для конкретной архитектуры процессора. Очевидным недостатком этого подхода является некоторая сложность и работоспособность реализации только для выбранного набора инструкций. Однако благодаря C макросам, код продолжает оставаться читаемым, как показано на рисунке 5. Данная оптимизация имеет большее влияние на Xeon Phi чем на 2S-E5, как показано на рисунке 9. Это происходит вследствие реализации SHIFT_MULT_INTR с помощью _mm512_alignr_epi32 на Xeon Phi, позволяющий использовать сдвиг вправо для 32-битных переменных (в одинарной точности). Таким образом, конечные элементы по скорейшей размерности могут вычислены для одного вектора с помощью всего 3 загрузок как показано на рисунках 4 и 5.
#pragma ivdep
for(TYPE_INTEGER ix=0;ix<ixEnd; ix+=SIMD_STEP){
SHIFT_MULT_INIT
SHIFT_MULT_INTR(1)
SHIFT_MULT_INTR(2)
SHIFT_MULT_INTR(3)
SHIFT_MULT_INTR(4)
SHIFT_MULT_INTR(5)
SHIFT_MULT_INTR(6)
SHIFT_MULT_INTR(7)
SHIFT_MULT_INTR(8)
MUL_COEFF_INTR(vertical_1, front_1, coeffVec[1])
MUL_COEFF_INTR(vertical_2, front_2, coeffVec[2])
MUL_COEFF_INTR(vertical_3, front_3, coeffVec[3])
MUL_COEFF_INTR(vertical_4, front_4, coeffVec[4])
MUL_COEFF_INTR(vertical_5, front_5, coeffVec[5])
MUL_COEFF_INTR(vertical_6, front_6, coeffVec[6])
MUL_COEFF_INTR(vertical_7, front_7, coeffVec[7])
MUL_COEFF_INTR(vertical_8, front_8, coeffVec[8])
REFRESH_NEXT_INTR
}
Рисунок 3. Исходный код вычислительного ядра с макросом, содержащий интринсики в dev08.
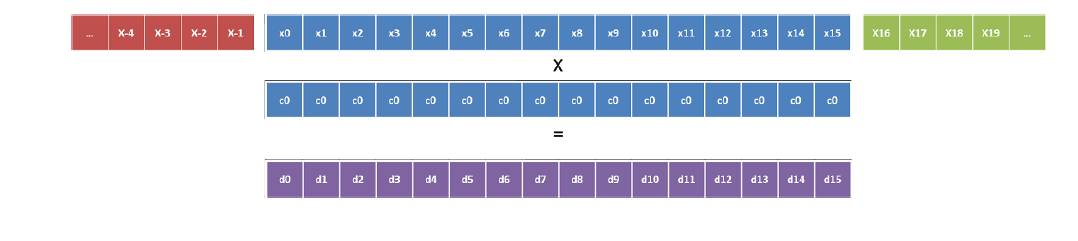
Рисунок 4. Векторизация по скорейшей размерности на Xeon Phi (коэффициент c0).
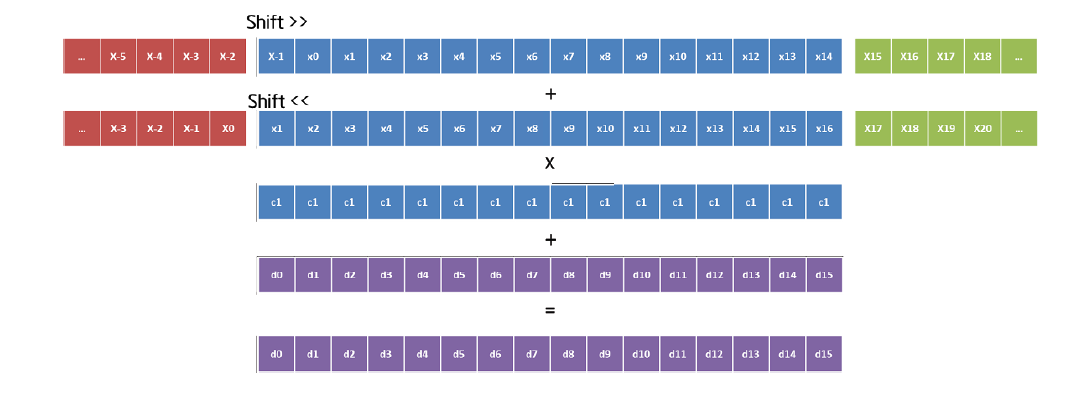
Рисунок 5. Векторизация по скорейшей размерности на Xeon Phi (коэффициент c1).
Сейчас мы исследуем возможности использования AVX2 инструкций для реализации эквивалентной оптимизации на новой архитектуре (на момент выпуска статьи — прим. переводчика) Intel Xeon E5 2600 v3. Для двух остальных размерностей векторизация проще. Для одного коэффициента нам требуется всего 4 загрузки, затем вектора суммируются и умножаются на данный коэффициент (рисунок 6). Это реализуется в рамках макроса MUL_COEFF_INTR.
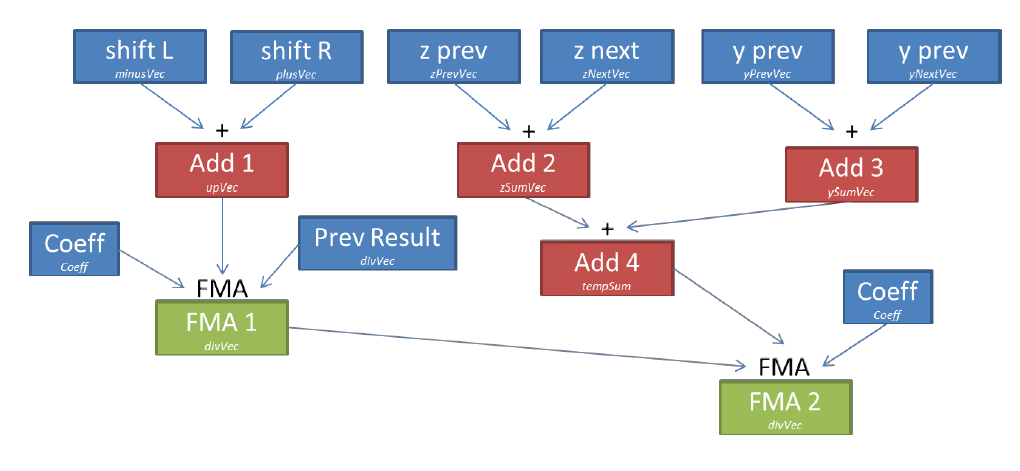
Рисунок 6. Операции для одного коэффициента в dev08.
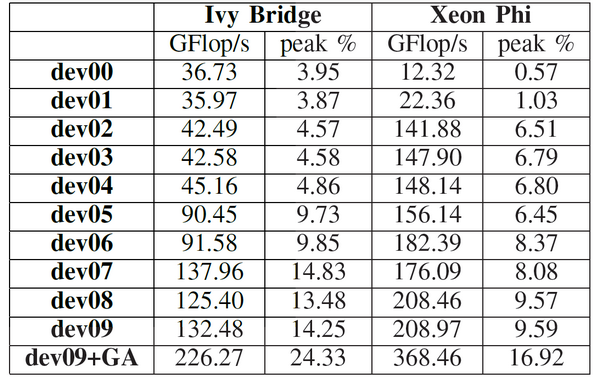
Рисунок 7. Производительность в GFlop/s в режиме ECC off/Turbo on для Xeon Phi и Turbo on для Ivy Bridge.
dev09: На Xeon Phi мы можем уменьшить количество временных переменных, тем самым снижая количество требуемых регистров (так называемое, register pressure, что ведет к spill/fill регистров — прим. переводчика) с помощью FMA инструкций (fused multiply add). Коэффициент может быть записан в один и тот же самый регистр на протяжении всех вычислений (6 FMA) и результат каждой FMA инструкции напрямую используется для следующего набора вычислений, ограничивая перемещение данных между регистрами (рисунок 8).
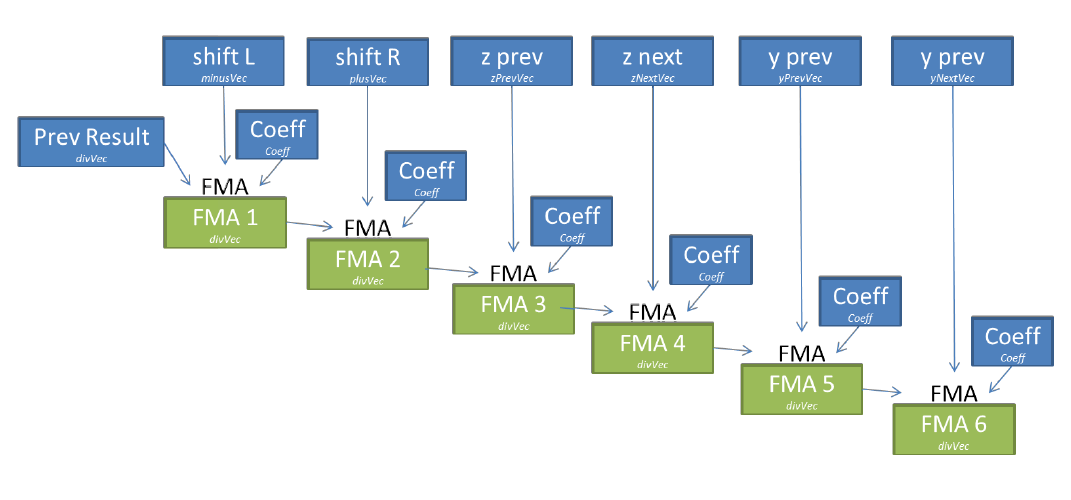
Рисунок 8. Операции для одного коэффициента в dev09.
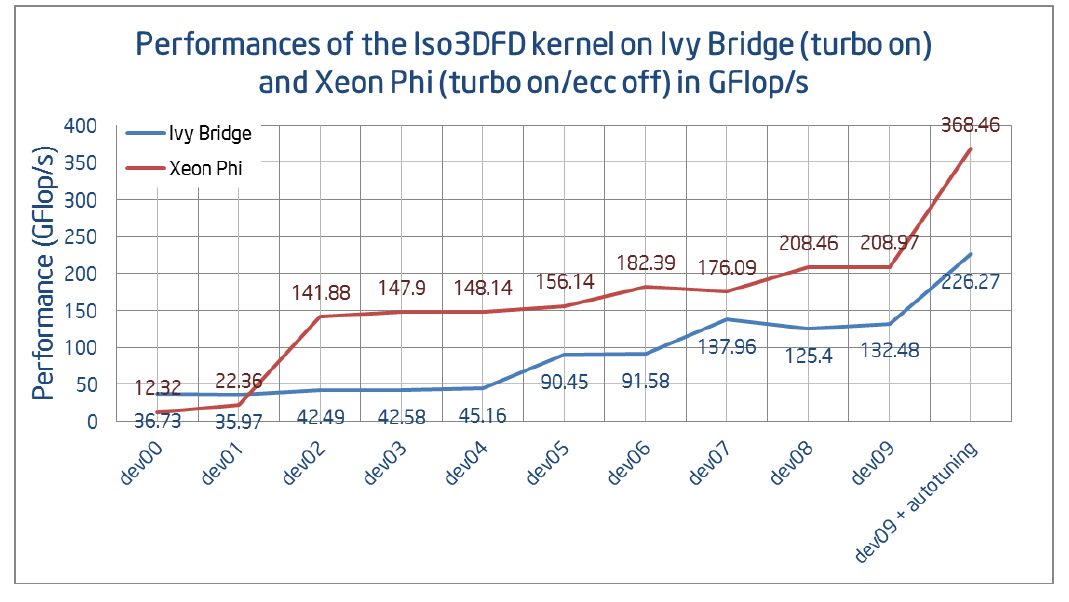
Рисунок 9. Производительность различных версий на 2S-E5 Ivy Bridge и Xeon Phi. Наиболее оптимизированная версия dev09 также была улучшена после применения генетического алгоритма автотюнинга.
Продолжение следует…
Автор: Intel






