Сортировка является одной из базовых операций при обработке данных, которая используется в самом широком спектре задач. В данной статье будет рассмотрена сеть обменной сортировки со слиянием Бэтчера для параллельной сортировки массива произвольного размера.
Введение
Сети сортировки – это вид алгоритмов сортировки, в которых порядок выполнения операций сравнения и их количество не зависит от значения элементов сортируемого массива. Они позволяют создавать масштабируемые параллельные алгоритмы сортировки больших объемов данных.
В сетях сортировки каждый элемент массива последовательно обрабатывается компараторами, которые сравнивают два элемента и, при необходимости, меняют их местами.
Сети сортировки принято изображать следующим образом. Сортируемые элементы массива обозначаются горизонтальными линиями данных, а компараторы – вертикальными отрезками, которые соединяют только две линии. На рисунке 1 ниже показана сеть сортировки для трех элементов и пример упорядочивания массива 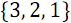 . Значение на каждой линии данных меняется по мере срабатывания соответствующего компаратора.
. Значение на каждой линии данных меняется по мере срабатывания соответствующего компаратора.
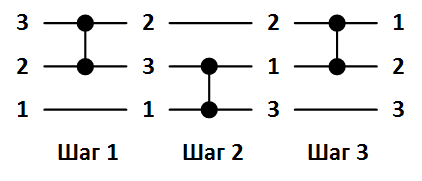
Рисунок 1. Сеть сортировки массива из 3 элементов.
На данный момент способ построения сетей, обладающих минимальным временем для произвольного числа входов, неизвестен, поэтому рассмотрим одну из наиболее быстродействующих масштабируемых сетей сортировки.
Сеть обменной сортировки со слиянием Бэтчера
Сети Бэтчера – наиболее быстродействующие из масштабируемых сетей. Для построения сети будем использовать следующий рекурсивный алгоритм.
При сортировке массива из  элементов с номерами
элементов с номерами 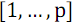 следует разделить его на две части: в первой оставить
следует разделить его на две части: в первой оставить 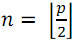 элементов с номерами
элементов с номерами 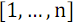 , а во второй
, а во второй 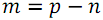 элементов с номерами
элементов с номерами 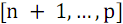 . Далее следует отсортировать каждую из частей (функция B) и объединить результаты сортировки (функция S).
. Далее следует отсортировать каждую из частей (функция B) и объединить результаты сортировки (функция S).
Рассмотрим данные функции подробнее.
B(array) – функция рекурсивного построения сети сортировки группы линий. Рекурсивно делит массив на два подмассива up и down из 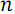 и
и 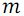 элементов соответственно, после чего вызывает функцию слияния S для этих подмассивов.
элементов соответственно, после чего вызывает функцию слияния S для этих подмассивов.
S(up, down) – функция рекурсивного слияния двух групп линий. В сети нечетно-четного слияния отдельно объединяются элементы массивов с нечетными номерами и отдельно с четными, после чего с помощью заключительной группы компараторов обрабатываются пары соседних элементов с номерами 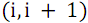 , где
, где 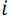 – натуральные числа от
– натуральные числа от 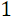 до
до 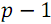 . Данные пары записываются в массив компараторов comparators для дальнейшего использования.
. Данные пары записываются в массив компараторов comparators для дальнейшего использования.
- Массивы типа T обозначаются как array(T).
- Считаем, что все функции работы с массивами определены в каком-нибудь array.h и делают ровно то, что написано в названии.
- Кроме функции array_push(): для векторов она добавляет переданное значение в конец массива, при необходимости выделяя память; для обычных массивов — записывает переданное значение после последнего записанного, начиная с нулевого.
void S(array(int) procs_up, array(int) procs_down)
{
int proc_count = array_size(procs_up) + array_size(procs_down);
if (proc_count == 1) {
return;
} else if (proc_count == 2) {
array_push(&comparators, ((pair_t){ procs_up[0], procs_down[0] }));
return;
}
array(int) procs_up_odd = array_new(array_size(procs_up) / 2 + array_size(procs_up) % 2, int);
array(int) procs_down_odd = array_new(array_size(procs_down) / 2 + array_size(procs_down) % 2, int);
array(int) procs_up_even = array_new(array_size(procs_up) / 2, int);
array(int) procs_down_even = array_new(array_size(procs_down) / 2, int);
array(int) procs_result = array_new(array_size(procs_up) + array_size(procs_down), int);
for (int i = 0; i < array_size(procs_up); i++) {
if (i % 2) {
array_push(&procs_up_even, procs_up[i]);
} else {
array_push(&procs_up_odd, procs_up[i]);
}
}
for (int i = 0; i < array_size(procs_down); i++) {
if (i % 2) {
array_push(&procs_down_even, procs_down[i]);
} else {
array_push(&procs_down_odd, procs_down[i]);
}
}
S(procs_up_odd, procs_down_odd);
S(procs_up_even, procs_down_even);
array_concatenate(&procs_result, procs_up, procs_down);
for (int i = 1; i + 1 < array_size(procs_result); i += 2) {
array_push(&comparators, ((pair_t){ procs_result[i], procs_result[i + 1] }));
}
array_delete(&procs_up_odd);
array_delete(&procs_down_odd);
array_delete(&procs_up_even);
array_delete(&procs_down_even);
array_delete(&procs_result);
}
void B(array(int) procs)
{
if (array_size(procs) == 1) {
return;
}
array(int) procs_up = array_new(array_size(procs) / 2, int);
array(int) procs_down = array_new(array_size(procs) / 2 + array_size(procs) % 2, int);
array_copy(procs_up, procs, 0, array_size(procs_up));
array_copy(procs_down, procs, array_size(procs_up), array_size(procs_down));
B(procs_up);
B(procs_down);
S(procs_up, procs_down);
array_delete(&procs_up);
array_delete(&procs_down);
}Код функций с нормальной подсветкой синтаксиса на гитхабе.
Приведем примеры.
Первый пример.
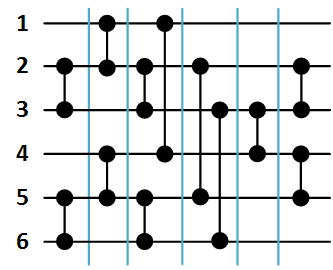
На рисунке 2 ниже представлена сеть сортировки массива из 6 элементов, сформированная в результате вызова функции B(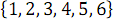 ).
).
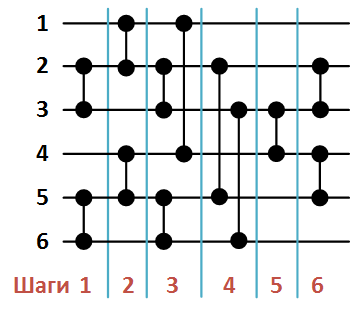
Рисунок 2. Сеть Бэтчера сортировки массива из 6 элементов.
При этом список компараторов в порядке их формирования функцией S будет следующим:
- (2, 3),
- (1, 2),
- (2, 3),
- (5, 6),
- (4, 5),
- (5, 6),
- (1, 4),
- (3, 6),
- (3, 4),
- (2, 5),
- (2, 3),
- (4, 5).
Второй пример.
Рассмотрим пример объединения двух упорядоченных массивов: 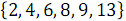 и
и 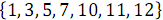 . На рисунке 3 ниже вертикальные блоки обозначают сети слияния, обрабатывающие нечетные и четные группы строк массивов.
. На рисунке 3 ниже вертикальные блоки обозначают сети слияния, обрабатывающие нечетные и четные группы строк массивов.
В результате объединения элементов, имеющих нечетные номера 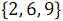 и
и 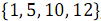 , получен упорядоченный массив
, получен упорядоченный массив 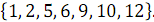 .
.
В результате объединения элементов, имеющих четные номера 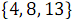 и
и 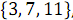 , получен упорядоченный массив
, получен упорядоченный массив 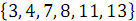 .
.
В результате выполнения последней группы компараторов получен полностью отсортированный массив: 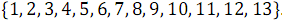 .
.
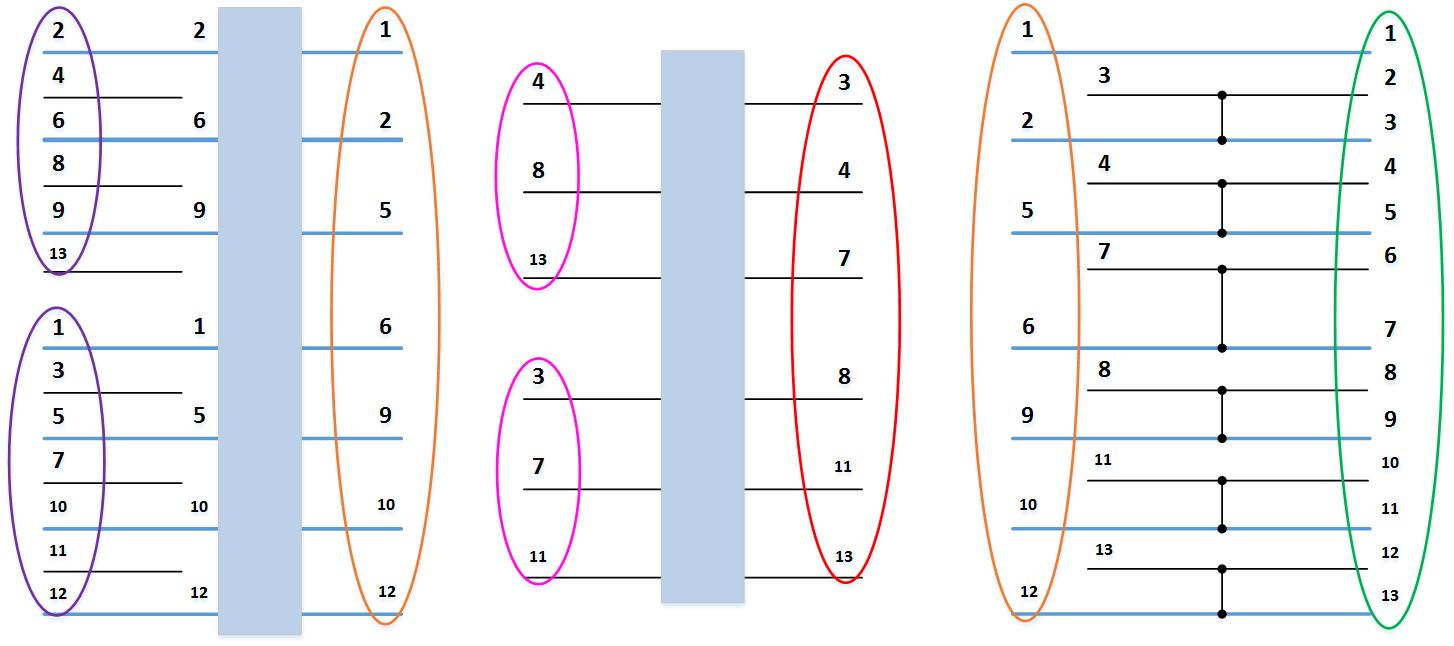
Рисунок 3. Сеть нечетно-четного слияния Бэтчера.
Сортировка больших массивов
В случае, если размер массива превышает число процессоров 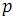 , на каждом процессоре будем хранить по
, на каждом процессоре будем хранить по 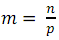 элементов массива. Сортировку будем выполнять в два этапа.
элементов массива. Сортировку будем выполнять в два этапа.
- Сортировка на каждом процессоре массива длиной
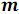 . Каждый процессор независимо от других выполняет процесс упорядочивания элементов массива. Сортировка выполняется наилучшим из доступных последовательных алгоритмов.
. Каждый процессор независимо от других выполняет процесс упорядочивания элементов массива. Сортировка выполняется наилучшим из доступных последовательных алгоритмов. - Слияние каждого отсортированного массива в соответствии с расписанием, заданным используемой сетью сортировки
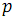 элементов, то есть на данном этапе осуществляется глобальная сортировка.
элементов, то есть на данном этапе осуществляется глобальная сортировка.
Рассмотрим второй этап подробнее. На рисунке 4 ниже каждая линия данных соответствует одному процессору, а каждый компаратор – компаратору слияния.
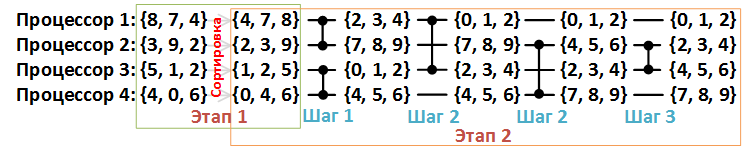
Рисунок 4. Пример сортировки массива {8, 7, 4, 3, 9, 2, 5, 1, 2, 4, 0, 6}, n = 12, p = 4.
Компаратор слияния принимает на вход два массива одинаковой длины и перераспределяет элементы в два новых массива таким образом, что первый из них содержит элементы с меньшими значениями, а второй – с большими.
В случае использования распределенной памяти, добавляется этап пересылки данных между процессорами:
- каждый из процессоров пересылает свой фрагмент массива процессору, подключенному к другому входу компаратора,
- процессор с меньшим номером выделяет из двух фрагментов
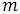 наименьших элементов, а процессор с большим номером –
наименьших элементов, а процессор с большим номером – 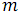 наибольших элементов.
наибольших элементов.
При необходимости будем дополнять массив фиктивными нулевыми элементами, чтобы длина сортируемого процессора была кратна числу процессоров.
Таким образом, первый этап можно записать как:
int proc_count; // всего процессоров
int elems_count; // всего элементов
int elems_count_new = elems_count + (elems_count % proc_count ? proc_count - elems_count % proc_count : 0);
int elems_per_proc_count = elems_count_new / proc_count;Тогда первый этап состоит всего из одной строки кода:
qsort(elems_result, elems_per_proc_count, array_item_size(elems_result), compare_uint32);А второй:
Затем на каждом процессоре формируется третий массив (elems_temp), состоящий из наименьших элементов (для первого процессора) или наибольших (для второго процессора).
После чего массив elems_temp записывается на место массива elems_result.
for (int i = 0; i < array_size(comparators); i++) {
pair_t comparator = comparators[i];
if (rank == comparator.a) {
MPI_Send(elems_result, elems_per_proc_count, MPI_UNSIGNED, comparator.b, 0, MPI_COMM_WORLD);
MPI_Recv(elems_current, elems_per_proc_count, MPI_UNSIGNED, comparator.b, 0, MPI_COMM_WORLD, &status);
for (int res_index = 0, cur_index = 0, tmp_index = 0; tmp_index < elems_per_proc_count; tmp_index++) {
uint32_t result = elems_result[res_index];
uint32_t current = elems_current[cur_index];
if (result < current) {
elems_temp[tmp_index] = result;
res_index++;
} else {
elems_temp[tmp_index] = current;
cur_index++;
}
}
swap_ptr(&elems_result, &elems_temp);
} else if (rank == comparator.b) {
MPI_Recv(elems_current, elems_per_proc_count, MPI_UNSIGNED, comparator.a, 0, MPI_COMM_WORLD, &status);
MPI_Send(elems_result, elems_per_proc_count, MPI_UNSIGNED, comparator.a, 0, MPI_COMM_WORLD);
int start = elems_per_proc_count - 1;
for (int res_index = start, cur_index = start, tmp_index = start; tmp_index >= 0; tmp_index--) {
uint32_t result = elems_result[res_index];
uint32_t current = elems_current[cur_index];
if (result > current) {
elems_temp[tmp_index] = result;
res_index--;
} else {
elems_temp[tmp_index] = current;
cur_index--;
}
}
swap_ptr(&elems_result, &elems_temp);
}
}Особенности ввода-вывода
Для ввода будем использовать функцию MPI_File_read_ordered(), которая последовательно считывает из файла равные фрагменты массива для каждого процессора. В случае, если данных из файла будет недостаточно, она не затрет фиктивные нули, которыми инициализирован массив.
Для вывода будем использовать аналогичную функцию MPI_File_write_ordered(), однако для каждого процессора необходимо высчитывать, сколько элементов он должен записать в файл. Такая необходимость возникает в случае, если длина сортируемого массива была не кратна числу процессоров.
Рассмотрим подробнее.

Рисунок 5. Пример распределения массива по процессорам. Необходимо вывести обведенные синим элементы.
Для каждого процессора будем вычислять смещение (переменная print_offset) относительно начала массива, с которого необходимо начать вывод, а также количество выводимых элементов (переменная print_count).
Возможны три случая.
- Процессор не выводит ничего, т. е. смещение — ноль, количество выводимых — ноль.
- Процессор выводит некоторые свои элементы, т. е. смещение — число пропускаемых элементов, количество выводимых — разность elems_per_proc_count и смещения.
- Процессор выводит все свои элементы массива, т. е. смещение — ноль, количество выводимых — elems_per_proc_count.
Рассмотрим вычисление смещения. Очевидно, что смещение равно нулю всегда, кроме процессора, на котором заканчивается количество пропускаемых элементов. Номер такого процессора вычисляется как отношение skip к elems_per_proc_count с отбрасыванием дробной части, а количество элементов, которые не нужно выводить данному процессору, как остаток от деления в указанном отношении.
Таким образом, после группировки всех условий получаем выражение для print_offset.
По приведенному ниже коду не составит труда разобраться в формуле для вычисления количества элементов.
// Количество элементов из общего числа, которые не нужно выводить.
int skip = elems_count_new - elems_count;
// Номер элемента, с которого начинается вывод для каждого процессора.
int print_offset = (skip / elems_per_proc_count == rank) * (skip % elems_per_proc_count);
// Количество выводимых процессором элементов.
int print_count = (skip / elems_per_proc_count <= rank) * elems_per_proc_count - print_offset;
// Число элементов выводит только один процессор с рангом 0.
MPI_File_write_ordered(output, &elems_count, rank == 0, MPI_UNSIGNED, &status);
// Последовательно выводим элементы на основе рассчитанных смещений и количеств для каждого процессора.
MPI_File_write_ordered(output, (unsigned char *)elems_result + print_offset * array_item_size(elems_result), print_count, MPI_UNSIGNED, &status);Тестирование 32-х битного приложения
Были сгенерированы файлы с случайными беззнаковыми целыми числами на разное число элементов, после чего результат работы программы сравнивался с эталонным ответом, полученным с помощью стандартной функции qsort().
В таблице ниже приведено сравнение скорости работы последовательного алгоритма с сортировкой Бэтчера на разном числе процессоров.
На стационарной машине (Intel Core i7-3770 (4 ядра, 8 потоков), 8 GB RAM):
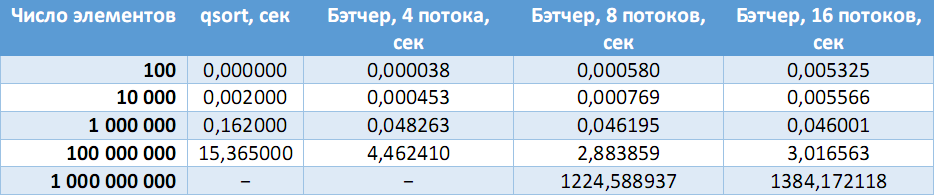
(Прочерки – ошибки выделения необходимого объема памяти).
Исходный код
Исходный код данной сортировки доступен на GitHub по следующей ссылке: https://github.com/zodinyac/batcher-sort. Там же можно найти генератор тестов и другие вспомогательные утилиты, описанные в README.md.
Использованная литература
- Якобовский М. В. Параллельные алгоритмы сортировки больших объемов данных.
- Якобовский М. В. Введение в параллельные методы решения задач.
- Тютляева Е. О. Интеграция алгоритма параллельной сортировки Бэтчера и активной системы хранения данных.
Автор: zodiac