Однострочники на Си/С++. Часть 2

Ранее я уже публиковал статью о Однострочниках на С++. Так в этом посте я хочу упомянуть ещё несколько алгоритмов, а также несколько реализаций алгоритма обмена двух чисел(с вычислением времени работы).
Всех заинтересовавшихся прошу под кат;)

1. Проверка на простоту

Для вызова этой функции надо написать prime(100, int(sqrt(100)));

bool prime(int n, int div) {
  return ( div == 1) ? true : (n % div != 0) && (prime(n, div-1));
}

Чтобы этого избежать можно создать функцию-оболочку:

bool prime(int n) {
  return ( n == 1 )? 0 : ( prime( n, int(sqrt(n))) ) ;
}

и тепер для вызова функции достаточно написать prime(100)

2. Код Грея

Кодом Грея называется такая система нумерования неотрицательных чисел, когда коды двух соседних чисел отличаются ровно в одном бите.

int codeGrey (int n) {
 return n ^ (n >> 1);
}

А также нахождение обратного кода Грея

int revCodeGrey (int g) { 
    int n;  
    for (n=0; g; n ^=g, g>>=1); 
    return n;
}

Коды Грея имеют несколько применений в различных областях:

• битный код Грея соответствует гамильтонову циклу по n-мерному кубу
• в решении задачи о Ханойских башнях
• применение в теории генетических алгоритмов

3. Вычисление биномиального коэффициента

Биномиальный коэффициент — это коэффициент в разложении бинома Ньютона 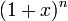по степеням x.

int binomialCoefficient(int k, int n) {
    return (n==k || k==0)?1:binomialCoefficient(k-1,n-1)+binomialCoefficient(k,n-1);
}

4. Нахождение степени делителя факториала

Даны два числа: [n] и [k]. Требуется посчитать, с какой степенью делитель [k] входит в число [n].

int factPow(int n, int k) {
    return (n)? (n/k + factPow(n/k, k)):0;
}

5. Возведение числа [a] в степень [b] по модулю [p].

nt powM(int a, int b, int p) {
    return b ? (a * powM(a-1, b, p) % p) : 1;
}

Также здесь можно использовать индийский алгоритм возведения в степень.

int powM(int a, int b, int p) {
    return b ? ((b&1?a:1)*powM(a*a, b/2, p) % p) : 1;
}

Мое исследование SWAPa

Вот мне пришла мысль исследовать разнообразные SWAPи, какой из них самый быстрый.
Тест SWAPов будет вот такой программкой

    int a=1, b=2;
    for(int i=0; i<=300000000; i++) {
       swap(&a, &b);
    }

где вместо swap, будут различные алгоритмы обмена двух значений.

SWAP0

Итак начнем пожалуй из STLивского, стандартного алгоритма:

template <class T> void swap0 ( T& a, T& b ) {
    T c(a); a=b; b=c;
}

его показатели были таковы:

   1,996 sec.
   1,986 sec.
   1,996 sec.

SWAP1

Следующим SWAPом будет так называемый XOR SWAP:

void swap1(int *a, int *b) {
    *a ^= ( *b ^= ( *a ^= *b ));
}

его показатели были таковы:

   3,603 sec.
   3,603 sec.
   3,608 sec.

SWAP2

void swap2(int *a, int *b) {
    *a += *b -= *a = *b - *a;
}

её показатели были таковы:

   3.728 sec.
   3.723 sec.
   3.728 sec.

SWAP3

void swap3(int *a, int *b) {
    *a /= *b = (*a= *a * (*b)) / (*b);
}

её показатели были таковы:

   7.878 sec.
   7.862 sec.
   7.862 sec.

SWAP4

void swap4(int *a, int *b) {
    *b= *a + *b - (*a = *b);
}

её показатели были таковы:

   2.012 sec.
   2.007 sec.
   2.012 sec.

SWAP5

void swap5(int *a, int *b) {
    *a=(*b=(*a=*b^*a)^*b)^*a;
}

её показатели были таковы:

  3.198 sec.
  3.213 sec.
  3.198 sec.

SWAP6

Ну, и ассемблерная вставка для компилятора GCC

void swap7(int *a, int *b) {
     asm volatile(
        "XOR   %%EAX,  %%EBX;      nt"
        "XOR   %%EBX,  %%EAX;      nt"
        "XOR   %%EAX,  %%EBX;      nt"
        :"=a"(*a),"=b"(*b)
        :"a"(*a),"b"(*b)
    );
}

её показатели были таковы:

   2.199 sec.
   2.153 sec.
   2.167 sec.

Как видим наша таблица исследований такова:

1. SWAP0 -  1.992 sec.
   

2. SWAP4 -  2.010 sec.
   

3. SWAP6 -  2.173 sec.
   

4. SWAP5 -  3.203 sec.
   

5. SWAP1 -  3.604 sec.
   

6. SWAP2 -  3.726 sec.
   

7. SWAP3 -  7.867 sec.
   

Автор: Oleksandr17