В прошлой статье Понятие системы и конструкции. Их место в проектировании информационных систем, посвященной конструкциям, я вкратце затронул герменевтический круг – это один из способов нашего , нацеленного на достижение понимания. Герменевтический круг состоит из двух направлений : анализа и синтеза.
Анализ – это процесс, при котором мы представляем изучаемый объект в виде множества его частей (изучаем различные конструкции, на которые можно разложить изучаемый объект).
Синтез — это обратная «сборка» объекта.
Утверждается, что чувство понимания достигается, когда, сделав разборку объекта (анализ), а затем его сборку (синтез), — субъект получает непротиворечивый результат. В той же статье я отметил, что стандарты, как правило, нацелены на описание только одного направления — анализа, но совершенно игнорируют второе направление – синтез.
Игнорирование процесса синтеза приводит к тому, что мы теряем способность делать проверку результатов анализа и начинаем мыслить шаблонами. Например, если нас спросить, из чего состоит велосипед, то довольно быстро найдется «правильный» ответ. Но если спросить: "Частью чего является велосипед?", – мы сильно затруднимся с ответом.
Множество шаблонов, которые мы заучиваем, касаются только одного направления движения – в сторону анализа и почти никогда – в сторону синтеза. Как только слышим вопросы: "Как устроено что-то?", "Как работает что-то?", – сразу в сознании возникает образ конструкции. Однако, также часто, как мы слышим вопрос: "Как устроен объект?", так же редко слышим вопрос: «В рамках какого контекста существует объект?», «Частью чего он является?» Поэтому нам легко даются ответы на одни вопросы, и с трудом на другие. Будь мы дисциплинированы в своем , мы бы также легко ответили на вопрос: "Частью чего является велосипед?", как и на вопрос: "Из чего состоит велосипед?" И самое главное — привели бы приблизительно одинаковое количество вариантов ответа как на один, так и на второй вопросы.
Где можно столкнуться с подобными вопросами на практике? Например, когда надо решить задачу описания предприятия в рамках какого-то контекста. Мы задаемся вопросом: "Частью чего является предприятие?" Ответов на этот вопрос много: предприятие может быть частью города, частью отрасли, частью холдинга. В конструкции каждого такого объекта предприятие играем свою уникальную роль и связано своими уникальными связями с различными контрагентами. Вы видели стандарты, в которых описан подход к моделированию различных конструкций, частью которых является исследуемый объект? Боюсь утверждать на все сто, но я, к своему стыду, таких стандартов не знаю. Их либо нет, либо они мало известны. Поэтому нет и фреймворков для работы с такого рода моделями. А потребность в такого рода инструментах есть, например, когда мы хотим анализировать связи наших контрагентов в рамках различных коллабораций.
Сформулируем требование к фреймворку, моделирующему конструкции:
Возможность один объект представить в виде различных конструкций, а также возможность один объект представить частью различных конструкций.
Следующее ограничение, которое нас сдерживает при моделировании конструкций, — это непонимание того, что такое множества объектов и как моделируется множество.
Множество – это одно из тех аксиоматических понятий, которое невозможно определить через другие понятия. Кантор сказал, что множество — это многое, мыслимое как целое.
Например, пусть есть множество объектов на космической станции, или множество живых организмов на Земле, или множество ракушек на пляже. Множество – это тоже объект учета, но специфический, отличный от объекта. Множество имеет состав. Что входит в состав множества? Ответ забавный: множество объектов. Получается какой-то порочный круг – множество объектов имеет состав, а состав состоит из множества объектов. Причина этого в том, что два разных понятия обозначены одним термином:
- Множество – это многое, мыслимое нами как целое (мат).
- Множество – синоним слова «много».
Получается, что множество (мат.) имеет состав, а в состав входит МНОГО объектов.
В разговорной речи мы никогда не употребляем термин множество в математическом смысле. Например, когда мы говорим, что на улице множество людей танцевало и пело, то, конечно, имеется ввиду множество как синоним слова много. Множество танцевать не может: на улице много людей танцевало и пело.
Другое дело сказать: Множество танцующих на улице людей имеет ненулевое пересечение со множеством поющих на улице людей. Понятно, что здесь идет речь о множестве во втором смысле этого слова. В разговорной речи такое не услышишь. При этом множество танцующих людей имеет состав. Этот состав включает в себя много танцующих людей.
Если в разговорной речи упоминают слово множество, имеют ввиду МНОГО объектов. Но МНОГО объектов, — это не множество. Множество в математическом смысле – это то, что мыслится как целое. Когда я попросил представить множество объектов на космической станции, большинство из вас представило разные объекты, которые можно там увидеть. Но это представление – не есть представление множества в математическом смысле. Это представление множества объектов в смысле МНОГО объектов. Множество в математическом смысле – это нечто иное. Это то, что представляется нами как единое целое. То, что вы представили много объектов, не дает вам представления о множестве. Вы представили состав множества. Теперь надо этот состав представить, как одно целое (для начала дать ему имя, например). Вот тут и кроется загадка множества – не всякий способен помыслить много объектов как одно целое, а создаваемый при этом образ не обязательно совпадет с образом, представленным другим субъектом. Именно поэтому так трудно объяснить, что такое множество. Именно поэтому проще ввести это понятие аксиоматически, без всякой опоры на здравый смысл.
Множество (так же, как и объект) необходимо в качестве инструмента для описания действительности. Понятие объект нам кажется понятным, только потому, что с этим понятием мы знакомимся в детстве, а множество – непонятным, потому что с ним мы знакомимся в институте, когда изучаем основы математики.
И тем не менее, понятие множества сидит в нас достаточно глубоко и известно каждому так же, как известно понятие объект, но не осознается нами так же ясно. Термин множество был введен не случайно, а как результат осознания этого факта.
Недавно я сделал попытку ввести понятие объекта так, как мы ввели бы его, будь оно нам совершенно неизвестно – при помощи классификации тех моделей, которые мы создаем в своем воображении, когда слышим упоминание об объекте. Эта попытка описана в статье: Строгое определение понятий: объект, состояние, событие, бизнес-операция и бизнес- функция. Попытка ввести понятие множества через модели, которые мы создаем в своем воображении, сделана мной в контексте моделирования конструкций в статье: Классификация конструкций: примеры и заблуждения. Эта статья вызвала бурную дискуссию, но, как мне показалось, обсуждали не классификацию, а вопросы, которые можно назвать скорее религиозными: например, должна ли конструкция обладать эмерджентностью, или может ли конструкция состоять из одного элемента? Понятно, что формальная теория систем не должна ограничивать себя каким-то узким кругом конструкций, иначе нельзя будет выполнять операции над системами. Из этого я сделал вывод, что рассуждения про множества довольно затруднительны и решил еще раз подробно остановиться на этой теме.
Когда мы говорили о конструкции, мы говорили о ней, как об:
- объекте,
- множестве объектов, связанными связями и мыслимыми как целое.
Вопрос: под множеством объектов в данном определении понимается что? Множество в смысле «математическое множество», или множество в смысле «много»? В прошлой статье я не акцентировал на этом внимание, теперь мы можем разобрать это определение более подробно.
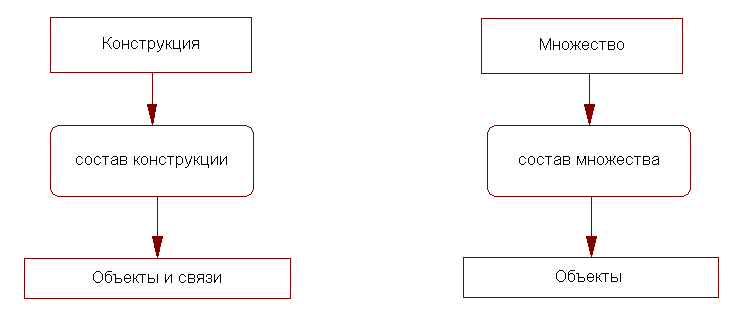
Мы видим, что определение конструкции практически повторяет определение множества: конструкция — это много объектов, мыслимых как единое целое. Множество в математическом смысле и конструкция – это объекты одного сорта. Состав множества – это много объектов, а состав конструкции — это много объектов и много связей. При этом множество – не есть много объектов, и конструкция – не есть много объектов и связей. Если мы говорим, что конструкция состоит из множества объектов, мыслимых как целое, имеется в виду, что состав конструкции включает в себя много объектов, но конструкция при этом– одна. Именно поэтому я сказал, что понятие множества сидит в нашем сознании глубоко, но не осознается нами так, как осознается понятие объекта.
Можно сказать и так: конструкция – это множество (в математическом смысле) объектов и связей между ними. Тогда мы не должны говорить о том, что его необходимо мыслить его как целое, потому что это требование включено в определение термина множества (в математическом смысле) и получается тавтология.
Поэтому определение конструкции можно дать как первым способом, так и вторым.
Чтобы яснее представить себе аналогию, которая есть между понятием множества и понятием конструкции, нарисуем картинку.
Множеству соответствует конструкция. Множество имеет состав, и конструкция имеет состав. В состав множества входит много объектов и в состав конструкции входит много объектов (связи – тоже объекты).
Поскольку такая аналогия напрашивается, то на конструкциях можно построить такую же алгебру, как и на множествах: конструкции можно складывать, искать их пересечения, вычитать. Чтобы такая алгебра имела место быть, надо добавить нулевой элемент, аналог пустого множества, — пустую конструкцию, состоящую из пустого множества элементов. Кроме того, надо будет допустить существование конструкции из одного элемента или из одной связи, что кажется контринтуитивно, но без этого не получится проводить операции на конструкциях. То есть, для проведения операций над конструкциями (и системами) мы должны принять по отношению к термину конструкция ту же аксиоматику, что и по отношению ко множеству. Это позволит нам соединять конструкции, разъединять их, искать пересечения и проч. Что забавно, в математике множества появились в ответ на вопрос: как моделировать реальность, в том числе и конструкции, но, спустя век мы так и не научились этим инструментом пользоваться!
Часто можно слышать такие выражения как: «Конструкция производит электроэнергию». Поскольку множество ничего не «может» делать, не имеет размера, ничего не весит, то все эти свойства может иметь либо объект, входящий в состав множества, либо объект, синтезированный на основе этого множества, но не само множество. Получается, что, когда мы говорим, что конструкция производит электроэнергию, мы имеем в виду либо какой-то ее элемент, либо объект, синтезированный на ее основе, но ни в коем случае не имеем в виду множество объектов и связей, мыслимых как целое! Это важно помнить, и это нам понадобится в следующих статьях.
В информационных системах, с которыми мне приходится иметь дело, нет встроенного механизма для моделирования множеств. Моделирование множества (присвоение ему имени, атрибутов, возможность работать с ним как с обычным объектом, вызывая его по имени, обращаться к его атрибутам, проводить операции сложения, вычитания и пересечения) пока реализуются вручную. Из этого следует, что и конструкции приходится моделировать вручную. Следующее требование к фреймворку, который имеет цель моделировать конструкции:
Способность моделировать множества и производить операции над ними.
В следующей статье так же подробно рассмотрим понятия «тип» и «атрибут».
Автор: Марк Мельник
