Прогнозирование продаж с использованием библиотеки Prophet, часть 2

Привет! Продолжаю знакомить вас с библиотекой Prophet в качестве инстурмента прогнозирования продаж. Первая часть тут.

Функции для критериев качества в нашей прогнозной модели будут выглядеть следующим образом:

def calcucate_mae(data_daily):
"**"Mean Absolute Error calculation"""
data_daily[' abs_error'] = data_daily['y'] - data_daily['yhat']
mae = round(np.mean (abs (data_daily[-predictions:][' abs_error'])), 2)
return mae

def calcucate_mape(data_daily):
""Mean Absolute Percentage Error calculation"""
data daily['abs error']
data_daily['y'] - data_daily[ 'yhat']
data_daily[' abs_error_pers'
data _daily[' abs_error'] * 100 / data _daily['y']
mape =
round (np mean(abs (data_daily[-predictions: ][*abs_error_pers'])), 2)
return mape

Далее выбираем для трех гипер-параметров значения, из которых будем компоновать модели. Параметр seasonality_prior_scale рекомендуется устанавливать в диапазоне до 10 и это и есть значение по умолчанию. Как было сказано ранее, сезонность в нашем рассматриваемом ряду очень выраженная, поэтому логично предположить, что значение параметра должно быть достаточно близко к максимальному. Можно было бы оставить только 10, но попробуем взять также уменьшенное в 2 раза, т.е. 5. 

Параметр changepoint_prior_scale изменяется в диапазоне от 0.01 до 0.5 – возьмем минимальное значение (0.01), дефолтное (0.05), максимальное (0.5) и еще два между ними. Последний параметр changepoint_range также имеет смысл брать максимально близким к максимуму – возьмем дефолтное 0.8, также 0.9 и 0.95. Итого набор гипер-параметров будет иметь вид:

season_scale_list
[5, 10]
changepoint_scale_list = [0.01, 0.05, 0.1, 0.25, 0.5]
changepoint_perc_list = [0.8, 0.9, 0.95]

Построим модели для каждого из сочетаний (всего будет 30) и выберем лучшую – для которой относительная ошибка выборки будет минимальной.

for sc in season scale list:
for cpc in changepoint_scale _list:
for cpp in changepoint_perc_list:
model ex = get _model(trend_type
'linear', season_scale = sC, changepoint_scale = cpc, changepoint _percent
= cpp)
forecast_ex = get forecast (model ex)
cmp_df_ex = forecast_ex. set_index( ds')[['yhat', 'yhat_lower', 'yhat_upper']].join(df.set_index(*ds'))
abs_ error_ex = calcucate_mae(cmp_df_ex)
rel error ex =
calcucate _mape (cmp_df_ex)
print(f'(sc}/{cpc}/{cpp}: mae - {abs_error_ex}, mape - (rel_error_ex]%°)

Лучшей стала модель с параметрами seasonality_prior_scale = 10, changepoint_prior_scale = 0.5 и changepoint_range = 0.95, что было ожидаемо – максимальная величина сезонных колебаний и максимальная доля исторических данных для обучения. Для данной модели построим прогноз.

model_ex 1 1 get_model(trend_type
'linear', season_scale = 10, changepoint_scale = 0.5, changepoint_percent = 0.9)

forecast_ex 1 = get_forecast (model_ex_1_1)

Относительная ошибка (MAPE) лучшей модели составила 0.98%, абсолютная (MAE) – 14.62.

abs_error_ex_1 = calcucate_mae(cmp_df_1)
abs_error_ex_1

14.62

rel_error_ex_1 = calcucate_mape(cmp_df_1)
print (f'{rel _error_ ex 1}%')

0.98%

Для сравнения ошибки худшей модели (с параметрами 5, 0.1, 0.8) составили, соответственно, абсолютная – 39.76 и относительная – 2.67%.

Результаты прогноза также удобно визуально оценить на графиках. Библиотека Prophet имеет собственные средства визуализации, например, с помощью метода plot_components, который позволяет посмотреть отдельно на все компоненты модели: тренд, сезонность, праздники.

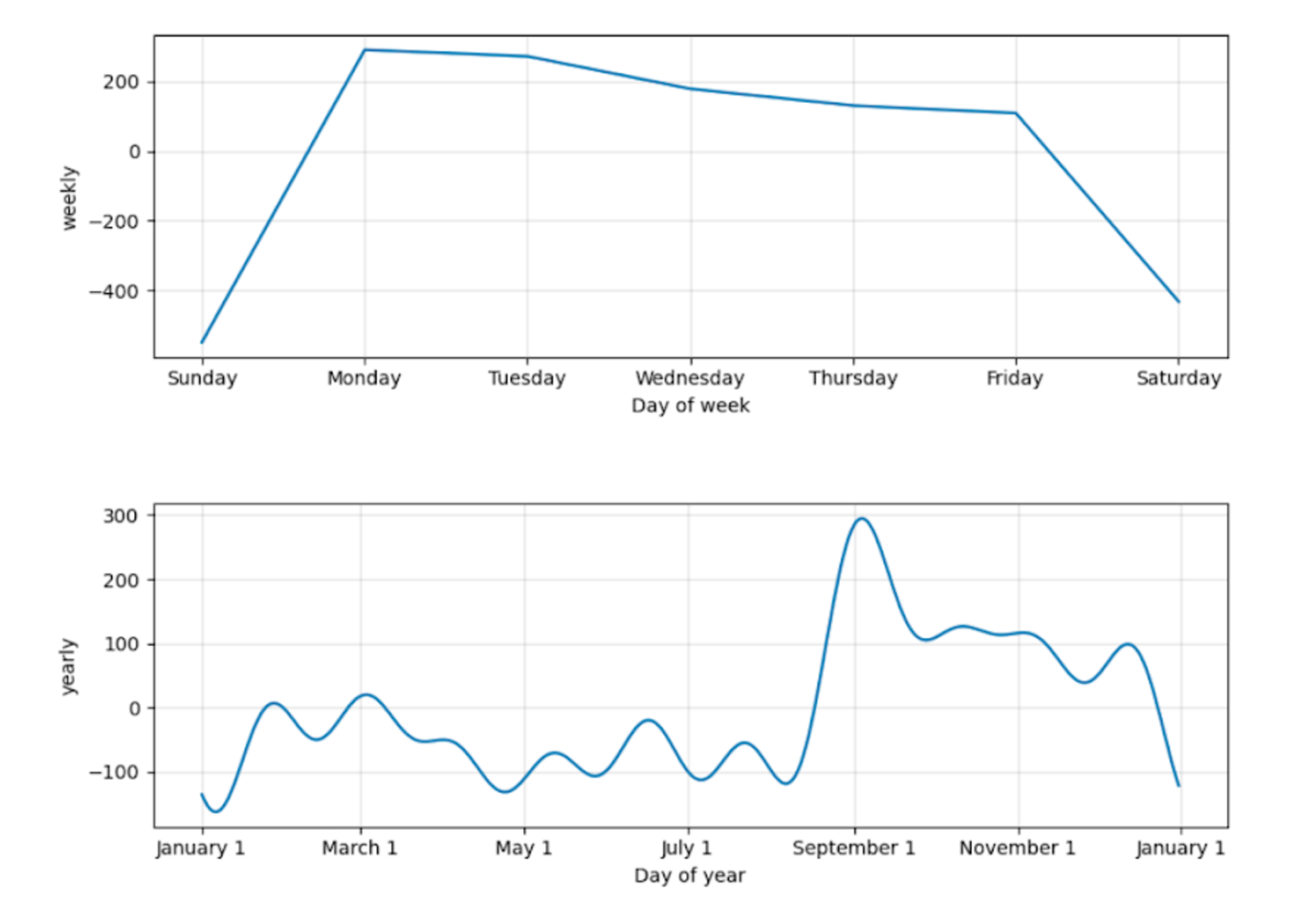
На графиках с праздниками (holidays) отображаются корректировки модели в основные периоды с большим количеством нерабочих дней – январь, конец февраля-начало марта, май.

Сезонность очень точно смоделирована – как по дням недели, так и по месяцам.

Помимо этого, с помощью стандартного метода Prophet.plot можно построить график, на котором будут отображены факт, основные расчетные прогнозные значения, а также границы доверительного интервала – на рисунке это области, выделенные светло-синим. Красным цветом выделены точки перелома тренда – тот самый гипер-параметр changepoint prior scale.

def get_model_plot (model, forecast):
fig = model.plot (forecast)
add_changepoints_to_plot(fig.gca(), model, forecast)
plt. show()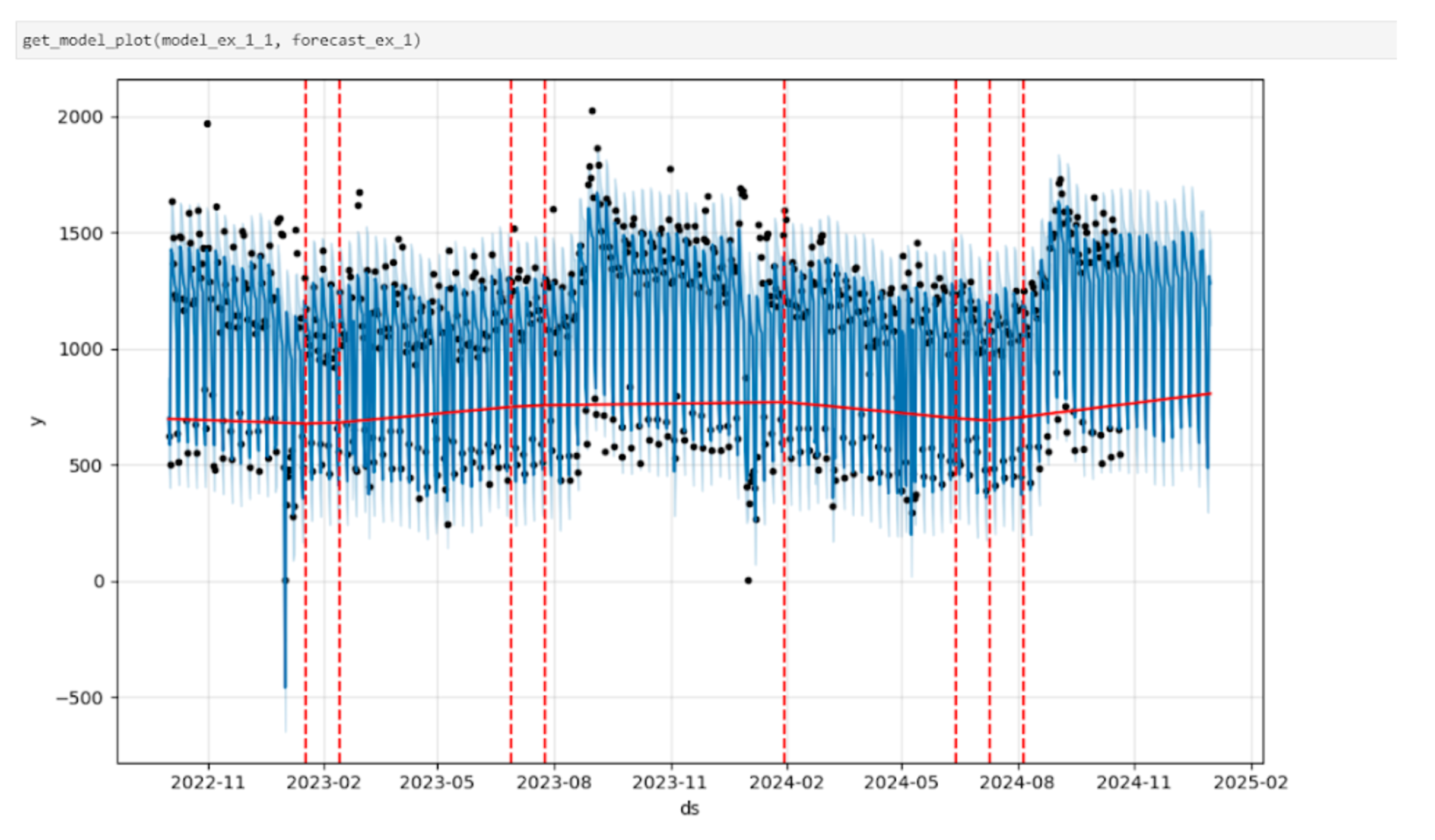

Также построим график, на котором отобразим факт только за последние 3 месяца (чтобы сделать его более информативным) и прогноз. 

Видим, что прогноз практически бесшовно продолжает ряд фактических значений. 

В целом модель демонстрирует вполне удовлетворительные результаты и вполне может служить рабочим вариантом для прогнозирования. Далее построим прогноз отдельно для каждого канала, филиала и сегмента.

Строим итоговую прогнозную модель

Данные по продажам FTTB-FMC хранятся и обновляются на кластере, для выгрузки используем PySpark (версия 3.2.4). Выгружаем данные по продажам за прошедшие 2 года, только FTTB и конвергентные минуса, без переездов, по каналам, филиалам и сегментам. Конкатенируем значения полей канал, филиал и сегмент для создания ключа, по которому будем формировать группы. Это будет основной дата-фрейм.

Как уже упоминалось ранее, все группы по каналу/филиалу/сегменту делятся в сущности на два больших кластера. Первый из них – это группы с четким и ярко выраженным трендом, сезонностью, стабильным количеством продаж – для них мы будем использовать модель с трендом, как рассмотрели выше. Второй кластер– это отсутствие тренда, практически нулевые продажи или мерцающего типа. Для таких групп будем использовать модель без тренда (growth = flat).

Чтобы присвоить каждой группе флаг наличия или отсутствия тренда, считаем среднее значение продаж за последние 3 месяца и, в случае если оно оказывается меньше установленного порогового значения, присваиваем индекс отсутствия тренда. Либо можно сделать наоборот – если значение больше, что тренд наличествует, в данном случае это не принципиально. Получаем таким образом второй дата-фрейм из двух столбцов – ключ группы и флаг наличия тренда.

Прогноз будем строить на 2 месяца вперед – текущий, в данном случае это октябрь и ноябрь 2024. Устанавливаем период для модели.

last _dt = sales_det _df['sale_date'].to_list()[-1]
month_end = last dt. replace (day = 1)
+ relativedelta(months 2)
relativedelta (days
=
-1)
days_delta = (month_end - last_dt). days
predictions = (month_end
-
last_dt). days + 1

В данном случае нет необходимости выделять модель и прогноз как мы делали на этапе подбора параметров, тогда функция для расчета прогноза будет иметь вид:

def get_forecast (filter_key, season_daily, season _weekly, season_yearly, trend_type, dt_type):
df part = sales_det_df[(sales_det_df[concat_key'] == filter_key) & (sales_det _df['sale_date'] ›= dt_type)][[' sale_date', 'sales']]
df_dates = current_dates. merge(df_part, on = 'sale date', how = 'left'). fillna(0)
df - pd. concat ([df_dates, future_dates])
df. columns
['ds', 'y']
predictions = (month end - last dt). days
train_df = df[:
predictions]
model = Prophet(
daily_seasonality = season _daily,
weekly_seasonality = season _weekly,
yearly_seasonality = season_yearly,
growth = trend_type,
# flat, Linear (default), logistic
seasonality_prior_scale = 10,
changepoint_prior_scale = 0.5,
# default = 10
changepoint_range = 0.95,
# default - 0.05
# default = 0.8
-
holidays = holidays russia
model.fit(train_df)
future = model. make future dataframe (periods = predictions)
forecast = model.predict (future)
cmp_df = forecast. set_index('ds')[['yhat', 'yhat_lower', 'yhat_upper']].join(df. set_index (*ds'))
cmp_df[' segm_market_chann'] = filter_key
return cmp df

Сначала строим модель для кластера с трендом – всего в нем будет 492 группы, то есть чуть меньше половины.

linear_trend_list = sales_last3_avg_df[sales_last3_avg_df['avg_low_ind"]==0]['concat_key'].to_list()
len(linear _trend list)

492

forecast_list_trend = []
for component in linear trend list:
forecast_part = get_forecast (filter_key
component, season_daily = True, season_weekly
= True,
trend_type
'linear', dt_type
True, season _yearly
dt_trend)
print(f'=========================
========={component}=======================
forecast_list_trend.append(forecast_part)
forecast_trend_total = pd. concat (forecast_list_trend)

Затем, от противного, находим перечень групп с отсутствующим трендом и для них также строим прогнозную модель.

filters_list_total = []
for m in markets list:
for c in channel list:
for s in segment list:
component
+ C + +S
filters_list_total. append (component)

no_trend_list = list(set(filters_list _total) - set (linear_trend_list))
len(no_trend_list)

522

forecast_list_no_trend = []
for component in no _trend list:
forecast part = get _forecast (filter_key
component, season daily = False, season weekly
False, season yearly = False,
trend type
'flat', dt type = dt_ no_trend)
print (f'==============#=*...=:
=========-{component}====-ass.........:
forecast list no trend. append (forecast part)
forecast_ no trend total =
pd. concat (forecast_list_no_trend)

Конкатенируем оба дата-фрейма и агрегируем данные по месяцам – прогнозная модель готова. Оценим качество прогноза на визуализации.

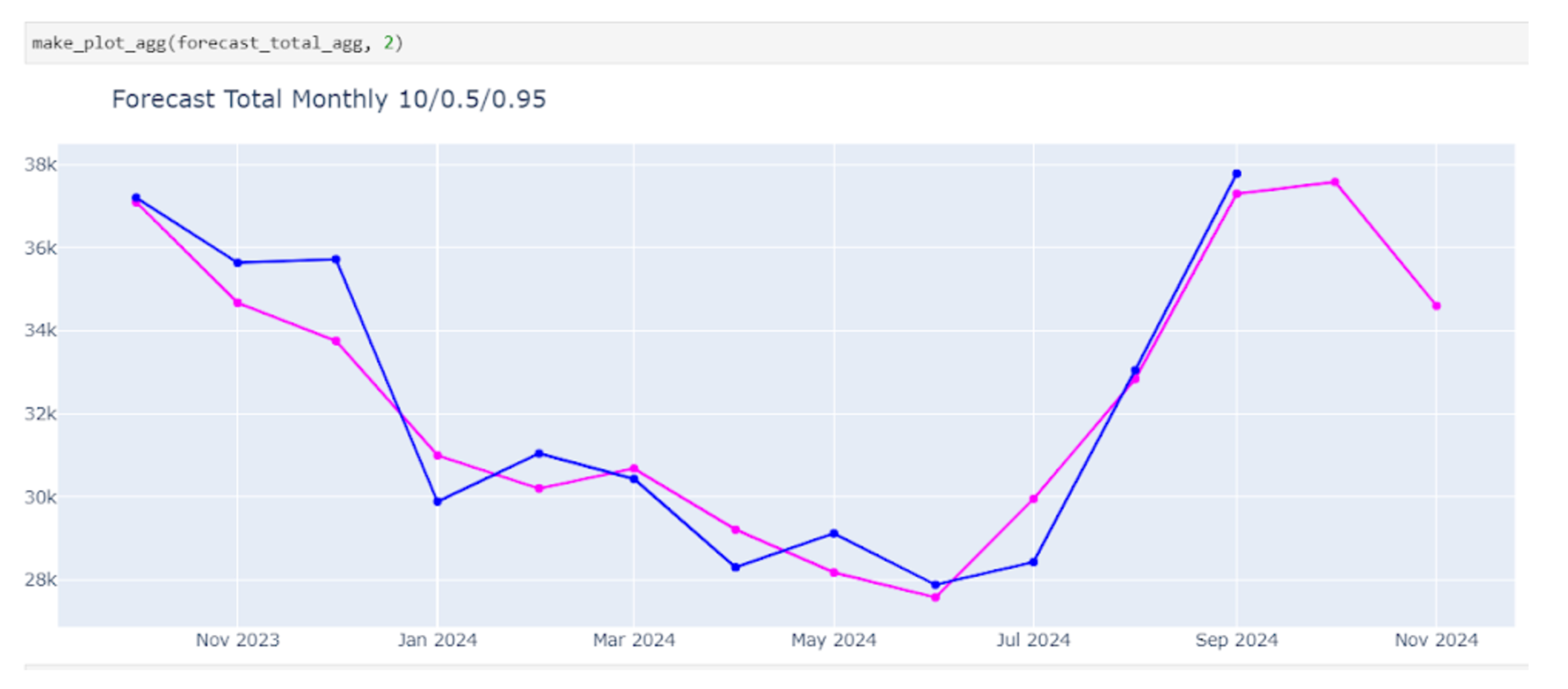
Для наглядности отобразим на графике только данные за 12 месяцев, с ноября 2023 по ноябрь 2024, фактические значения – это синяя линяя и прогнозные – сиреневая. На график видно, что прогноз достаточно хорошо описывает имеющиеся исторические данные – есть эффект сглаживания, прогноз повторяет тренд и сезонность.

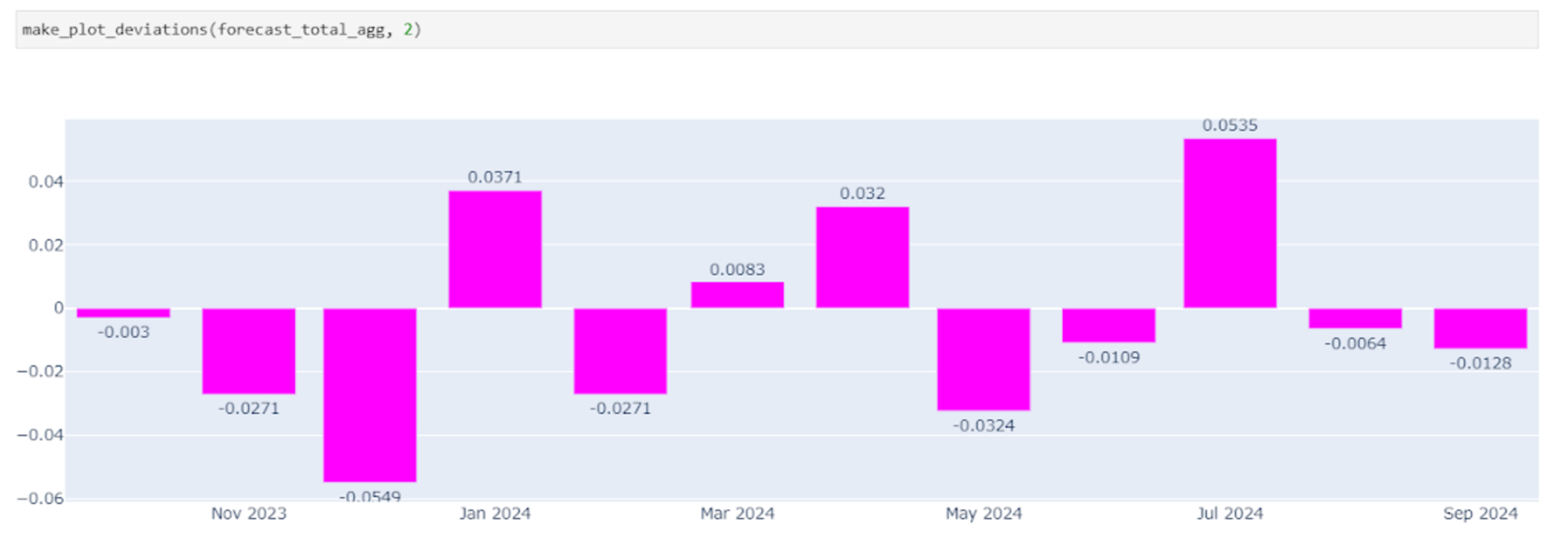
На этом графике представлены отклонения прогноза от факта за выбранный период. Видно, что максимальные отклонения приходятся на декабрь 2023, когда прогноз оказался ниже и в июле 2024, когда, наоборот, прогноз оказался завышен. В данном случае эти отклонения не стоит считать критичными – например, касательно июля все объясняется структурными изменениями в одном из каналов и связанной с этим практически полной остановкой продаж. 

Абсолютная ошибка и относительная ошибка, рассчитанные по агрегированным данным, составили, соответственно, 800.74 и 2.55%. 

В целом могу сказать, что прогнозная модель Phophet заслуживает высокой оценки и вполне подходит для моих ежедневных задач.

Итоги

Подводя итог, еще раз отметим достоинства модели Phophet. Самое главное – это интерпретируемость и гибкость. Модель позволяет выбрать функцию для тренда, учесть сразу все варианты сезонности, управлять гипер-параметрами, причем все компоненты модели представлены в «человеко-интерпретируемом» виде. Очень важная особенность – возможность добавлять аномальные дни, причем есть возможность корректировать поведение модели не только в эти указанные дни, но и в заданное количество дней до и после. Подобные вещи позволяют делать модель более гибкой.

В модель Phophet можно добавлять факторы (или регрессоры). В моей задаче мы не использовали регрессоры или, точнее, использовали в качестве фактора только время, но все же считаю важным отметить это преимущество. Например, если прогнозировать выручку или выживаемость, то в качестве фактора можно добавить активную базу абонентов, пользователей услуги и т.п.

Еще одно преимущество Phophet заключается в том, что модель хорошо обучается на коротких временных рядах, менее 100 наблюдений. На самом деле, чтобы построить приемлемый вариант прогноза на Phophet достаточно иметь хотя бы 12 наблюдений (то есть 1 год по месяцам), не всякая прогнозная модель способна на таком объеме исторических данных построить что-то адекватное.

Теперь о недостатках модели. В первую очередь я бы выделила не слишком высокую скорость. Одна итерация считается примерно за 3-5 секунд, соответственно, в моем случае с учетом 1000+ итераций весь расчет занимает больше часа. 

Следующий недостаток – это невозможность учесть в явном виде авторегрессию, как, например, это делается в моделях SARIMA. Как вариант, если учитывать авторегрессионные процессы необходимо, то можно использовать библиотеку Neural Prophet, но в рамках просто Prophet авторегрессию не добавить.

И последнее, что относится не только к Phophet, но и вообще к подобному классу моделей – они обладают достаточной степенью устойчивости при небольших или даже средних колебаниях, но, конечно, не могут справиться с каким-то серьезными изломами тренда. Например, во время пандемии в 2020-м многие тенденции оказались нарушены – в некоторых каналах продажи были остановлены. Подобные кризисные явления не способна описать модель, базирующаяся на трендах. Для таких случаев подходят адаптивные модели, вроде экспоненциального сглаживания.