Данный текст является продолжением серии статей, посвященных краткому описанию основных методов анализа данных. В предыдущий раз мы осветили методы классификации, сейчас рассмотрим способы прогнозирования. Под прогнозированием будем понимать поиск конкретного числа, которое ожидается получить для нового наблюдения или для будущих периодов. В статье указаны названия методов, их краткое описание и скрипт на Python. Конспект может быть полезен перед собеседованием, в соревновании или при запуске нового проекта. Предполагается, что аудитория знает эти методы, но имеет необходимость быстро освежить их в памяти.
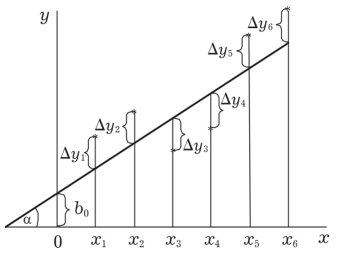
Регрессия, оцененная методом наименьших квадратов. Осуществляется попытка представить зависимость одного фактора от другого в виде уравнения. Коэффициенты оцениваются путем минимизации функции потерь (ошибки).
Если решить это уравнение, то можно найти оцениваемые параметры:

Графическое представление:
Если данные обладают свойствами Гаусса-Маркова:
— математическое ожидание ошибки равно 0
— гомоскедастичность
— отсутствие мультиколлинеарности
— детерминированная величина
— ошибка нормально распределена
То по теореме Гаусса-Маркова оценки будут иметь следующие свойства:
- Линейность — при линейном преобразовании вектора Y оценки также изменятся линейно.
- Несмещенность — при увеличении объема выборки математическое ожидание стремится к истинному значению.
- Состоятельность — при увеличении объема выборки оценки стремятся к их истинному значению.
- Эффективность — оценки обладают наименьшей дисперсией.
- Нормальность — оценки нормально распределены.
#imports
import statsmodels.api as sm
#model fit
Y = [1,3,4,5,2,3,4]
X = range(1,8)
X = sm.add_constant(X)
model = sm.OLS(Y,X)
results = model.fit()
#result
print(results.summary())
results.predict(X)-Обобщенный мнк GLS. Используется, когда не выполняются условия Гаусса-Маркова о гомоскедастичности (постоянстве дисперсии) остатков и некоррелированности остатков между собой. Цель GLS — учесть значения ковариационной матрицы остатков путем корректировки расчета параметров уравнения регрессии. Матрица оцениваемых параметров:
$$display$$a^* = (X^TΩ^{-1}X)^{-1}X^TΩ^{-1}Y$$display$$
где Ω — ковариационная матрица остатков. Отметим, что при Ω = 1 получим обычный МНК
#imports
import statsmodels.api as sm
from scipy.linalg import toeplitz
#model fit
data = sm.datasets.longley.load(as_pandas=False)
data.exog = sm.add_constant(data.exog)
ols_resid = sm.OLS(data.endog, data.exog).fit().resid
res_fit = sm.OLS(ols_resid[1:], ols_resid[:-1]).fit()
rho = res_fit.params
order = toeplitz(np.arange(16))
sigma = rho**order
gls_model = sm.GLS(data.endog, data.exog, sigma=sigma)
gls_results = gls_model.fit()
#result
print(gls_results.summary())
gls_results.predict-Взвешенный мнк wls. Используется, когда не выполняется эффективность оценок (есть гетероскедастичность) то есть первым шагом мы, взвешиваем наблюдения на их дисперсию, и далее применяем обычный МНК.
#imports
import statsmodels.api as sm
#model fit
Y = [1,3,4,5,2,3,4]
X = range(1,8)
X = sm.add_constant(X)
wls_model = sm.WLS(Y,X, weights=list(range(1,8)))
results = wls_model.fit()
#result
print(results.summary())
results.predict-Двухшаговый мнк tsls. Дисперсия для wls, как правило, неизвестна, поэтому на первом шаге мы ее оцениваем, а потом применяем wls. Такой подход также помогает решить проблему эндогенности.
#imports
from linearmodels import IV2SLS, IVLIML, IVGMM, IVGMMCUE
from linearmodels.datasets import meps
from statsmodels.api import OLS, add_constant
#model fit
data = meps.load()
data = data.dropna()
controls = ['totchr', 'female', 'age', 'linc','blhisp']
instruments = ['ssiratio', 'lowincome', 'multlc', 'firmsz']
data['const'] = 1
controls = ['const'] + controls
ivolsmod = IV2SLS(data.ldrugexp, data[['hi_empunion'] + controls], None, None)
res_ols = ivolsmod.fit()
#result
print(res_ols)
print(res_ols.predict)-ARIMA. Модель временных рядов. Auto-regression (зависит от Y в прошлом периоде) integrated (берутся разности для избавления от нестационарности — когда есть единичные корни, то есть тренд или цикличность) moving average (зависимость от остатка в прошлом периоде).
#imports
from pandas import read_csv
from pandas import datetime
from pandas import DataFrame
from statsmodels.tsa.arima_model import ARIMA
from matplotlib import pyplot
#model fit
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
model = ARIMA(series, order=(5,1,0))
model_fit = model.fit(disp=0)
#result
print(model_fit.summary())
model_fit.forecast()
-GARCH . General autoregression conditional heteroscedastic — применяется, когда во временных рядах есть гетероскедастичность.
#imports
import pyflux as pf
import pandas as pd
from pandas_datareader import DataReader
from datetime import datetime
#model fit
jpm = DataReader('JPM', 'yahoo', datetime(2006,1,1), datetime(2016,3,10))
returns = pd.DataFrame(np.diff(np.log(jpm['Adj Close'].values)))
returns.index = jpm.index.values[1:jpm.index.values.shape[0]]
returns.columns = ['JPM Returns']
#result
model = pf.GARCH(returns,p=1,q=1)
x = model.fit()
x.summary()Если упущен какой-либо важный метод, пожалуйста, напишите об этом в комментариях и статья будет дополнена. Спасибо за внимание.
Автор: Илья Герасимов



