При изучении Data Science, я решил составить для себя конспект по основным приемам, используемым в анализе данных. В нем отражены названия методов, кратко описана суть и приведен код на Python для быстрого применения. Готовил конспект для себя, но подумал, что кому-то это также может быть полезно, например, перед собеседованием, в соревновании или при запуске нового проекта. Рассчитано на аудиторию, которая в целом знакома со всеми этими методами, но имеет необходимость освежить их в памяти. Статья под катом.
-Наивный байесовский классификатор. Формула расчета вероятности отнесения наблюдения к тому или иному классу:
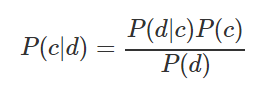
Например, нужно рассчитать вероятность, что спортивный матч состоится при условии, что погода солнечная. Исходные данные и расчеты приведены в таблице ниже:
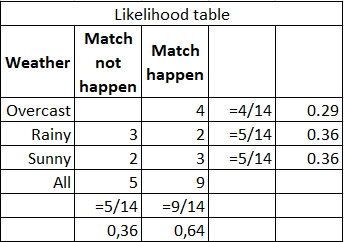
Можно посчитать по формуле (3/9) * (9/14) / (5/14) = 60%, или просто из здравого смысла 3/(2+3)=60%. Сильные стороны — легко интерпретировать результат, подходит для больших выборок и мультиклассовой классификации. Слабые стороны — не всегда выполняется предположение о независимости характеристик, характеристики должны составлять полную группу событий.
#imports
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
#model fit
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
#result
print("Number of mislabeled points out of a total %d points : %d"
% (X_test.shape[0], (y_test != y_pred).sum()))
-Метод ближайших соседей. Классифицирует каждое наблюдение по степени похожести на остальные наблюдения. Алгоритм является непараметрическим (отсутствуют ограничения на данные, например, функция их распределения) и использует ленивое обучение (не применяются заранее обученные модели, все имеющиеся данные используются во время классификации).
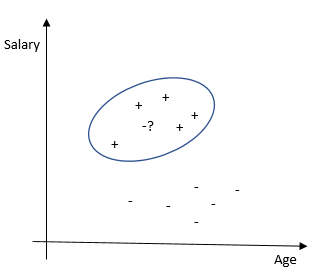
Сильные стороны — легко интерпретировать результат, хорошо подходит для задач с малым количеством объясняющих переменных. Слабые стороны — невысокая точность по сравнению с другими методами. Требует значительных вычислительных мощностей при большом количестве объясняющих переменных и больших выборках.
#imports
from sklearn.neighbors import KNeighborsClassifier
#model fit
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X, y)
#result
print(neigh.predict([[1.1]]))
print(neigh.predict_proba([[0.9]]))
-Метод опорных векторов (SVM). Каждый объект данных представляется как вектор (точка) в p-мерном пространстве. Задача — разделить точки гиперплоскостью. То есть, можно ли найти такую гиперплоскость, чтобы расстояние от неё до ближайшей точки было максимальным. Искомых гиперплоскостей может быть много, поэтому полагают, что максимизация зазора между классами способствует более уверенной классификации.
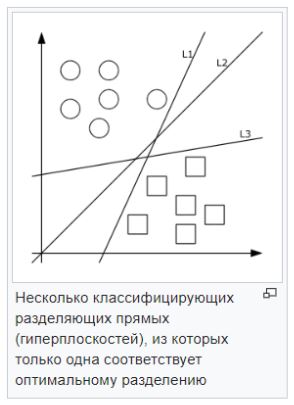
Сильные стороны — Эффективен при большом количестве гиперпараметров. Способен обрабатывать случаи, когда гиперпараметров больше, чем количество наблюдений. Существует возможность гибко настраивать разделяющую функцию. Слабые стороны — в случае, когда наблюдений меньше, чем объясняющих переменных, необходимо применять методы регуляризации, чтобы не переобучить модель. Также этот метод напрямую не дает вероятностных оценок.
#imports
from sklearn import svm
#model fit
X = [[0, 0], [1, 1]]
y = [0, 1]
clf = svm.SVC()
clf.fit(X, y)
#result
clf.predict([[2., 2.]])
-Деревья решений. Разделение данных на подвыборки по определенному условию в виде древовидной структуры. Математически разделение на классы происходит до тех пор, пока не найдутся все условия, определяющие класс максимально точно, т. е. когда в каждом классе отсутствуют представители другого класса. На практике используется ограниченное количество характеристик и слоев, а ветви всегда две.
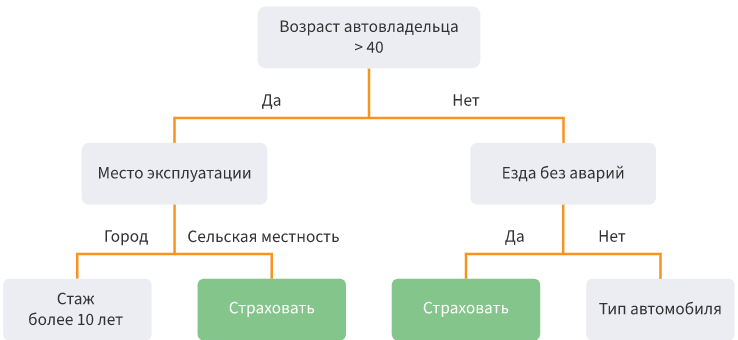
Сильные стороны — возможно моделировать сложные процессы и легко их интерпретировать. Возможна мультиклассовая классификация. Слабые стороны — легко переобучить модель, если делать много слоев. Выбросы могут повлиять на точность, решение этих проблем — обрезать нижние уровни.
#imports
from sklearn.datasets import load_iris
from sklearn import tree
#model fit
X, y = load_iris(return_X_y=True)
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X, y)
#result
tree.plot_tree(clf.fit(iris.data, iris.target)) -Случайный лес/Ансамбль деревьев. Это много бустингов и деревьев решений объединенных вместе. Бустинг — случайная выборка из базовой выборки. За счет большого числа таких подвыборок (random patching) и построения на каждой своей модели увеличивается качество финальной модели за счет усреднения. Для оценки качества модели нужно применять oob-оценку.
Сильные стороны: нечувствительность к выбросам, малые требования к предобработке данных, к масштабированию, небольшая чувствительность к гиперпараметрам, разброс модели меньше, а значит она не склонна к переобучению. Так как построение деревьев независимое, то вычисления можно распараллелить. Слабые стороны — потребляет память и время, чтобы считать и хранить много деревьев. Не применять, когда признаков очень много (больше 100 000), в этом случае лучше — регрессии.
#imports
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
#model fit
X, y = make_classification(n_samples=1000, n_features=4,
n_informative=2, n_redundant=0,
random_state=0, shuffle=False)
clf = RandomForestClassifier(max_depth=2, random_state=0)
clf.fit(X, y)
#result
print(clf.feature_importances_)
print(clf.predict([[0, 0, 0, 0]]))-Метод градиентного спуска. Итерационный алгоритм минимизации функции потерь (по умолчанию hinge loss function). Алгоритм также применяется в задачах прогнозирования.
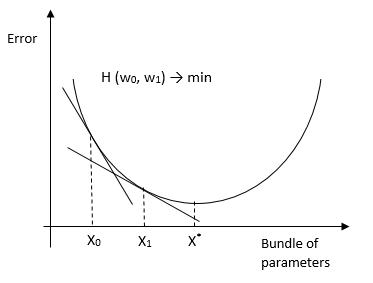
Также есть версия стохастического градиентного спуска, который применяется при больших выборках. Его суть в том что он считает производную не по всей выборке, а по каждому наблюдению (online learning) (или по группе наблюдений mini-batch) и меняет веса. В итоге он приходит в тот же оптимум что и при обычном ГС. Существуют методы применения ГС для МНК, логит, тобит и других методов (доказательства).
Сильные стороны: высокая точность классификации и прогнозирования, подходит для мультиклассовой классификации. Слабые стороны — чувствительность к параметрам модели.
#imports
from sklearn.linear_model import SGDClassifier
#model fit
X = [[0., 0.], [1., 1.]]
y = [0, 1]
clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
clf.fit(X, y)
#result
clf.predict([[2., 2.]])
clf.coef_
clf.intercept_-Градиентный бустинг. Это ансамбли моделей. Строятся регрессии или деревья решений и минимизируется функция потерь, как в градиентном спуске. Используется, когда выборка помещается в память, есть смесь разных признаков.
Сильные стороны: высокая точность классификации и прогнозирования, подходит для мультиклассовой классификации, не чувствителен к выбросам, способен решать задачи ранжирования. Слабые стороны — требователен к ресурсам компьютера.
#imports
import numpy as np
import matplotlib.pyplot as plt
from sklearn import ensemble
from sklearn import datasets
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error
#model fit
boston = datasets.load_boston()
X, y = shuffle(boston.data, boston.target, random_state=13)
X = X.astype(np.float32)
offset = int(X.shape[0] * 0.9)
X_train, y_train = X[:offset], y[:offset]
X_test, y_test = X[offset:], y[offset:]
params = {'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 2,
'learning_rate': 0.01, 'loss': 'ls'}
clf = ensemble.GradientBoostingRegressor(**params)
clf.fit(X_train, y_train)
#result
mse = mean_squared_error(y_test, clf.predict(X_test))
print("MSE: %.4f" % mse)-Логистическая регрессия/logit. Используется для классификации от 0 до 1, доказывается методом максимального правдоподобия (log likelihood). ММП — это вероятность получить Y при заданных Х и найденных параметрах w.
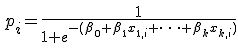
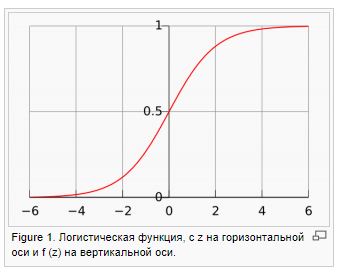
Сильные стороны: хорошо работает, когда гиперпараметры коррелируют с объясняющей переменной. Слабые стороны — подходит для бинарной классификации, слабо работает при эндогенности.
#imports
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
#model fit
X, y = load_iris(return_X_y=True)
clf = LogisticRegression(random_state=0).fit(X, y)
clf.predict(X[:2, :])
#result
clf.predict_proba(X[:2, :])
clf.score(X, y) -Probit. Отличается от логит модели тем, что предполагает нормальность распределения гиперпараметров, в то время, как логит модель предполагает логистическое распределение.
#imports
import statsmodels
#model fit
result_3 = statsmodels.discrete.
discrete_model.Probit(labf_part, ind_var_probit )
#result
print(result_3.summary()) -Tobit. Применяется, когда зависимая переменная ограничена и непрерывна.
#imports
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
import pandas as pd
from tobit import *
#model fit
tr = TobitModel()
#result
tr = tr.fit(x, y, cens, verbose=False)
tr.coef_Если упущен какой-либо важный метод, пожалуйста, напишите об этом в комментариях. Планируется выпуск статей по обучению без учителя, методам предобработки, методам оценки качества модели, интересным терминам и доказательствам. Спасибо за внимание.
Автор: Илья Герасимов