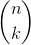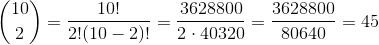Предисловие
Прежде всего хочу сказать, мне всего 14 лет. Я надеюсь, что информация, которой поделюсь, будет для кого-то интересна.
Речь пойдет о некоторых задачах комбинаторики.
Сколько вариантов расставить n предметов?
Способ №1
Первое, что приходит на ум обычному человеку: «Возьму-ка я 3 предмета и начну их расставлять в ряд. Сколько разных комбинаций получится — столько вариантов расстановок и есть». Да, это так. Но есть способ, который по своей простоте опережает приведенный ранее способ.
Способ №2
Факториал — количество способов расставить n предметов.
Факториал высчитывается перемножением чисел от 1 до n.
Обозначается n! (читать как факториал n).
Допустим, нам нужно узнать, сколько вариантов в расстановке 10 предметов. Умножаем: 1x2x3..x10
Получим: 10! = 3628800
Как из n предметов выбрать k предметов?
Способ №1
Допустим, вы — организатор лотереи. Из 10 участников вам нужно выбрать 2 победителя. Вы можете узнать количество способов сделать это.
Так же как и в случае с факториалом, можно посчитать вручную. Выбирать n предметов, пока не иссякнут все варианты.
Цитирую: но есть способ, который по своей простоте опережает приведенный ранее способ.
Способ №2
Число сочетаний — это количество способов из n предметов выбрать k предметов.
Обозначается так:
Высчитывается по формуле: 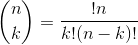
Итак, сколько же способов из 10 участников выбрать 2 победителя?
Числа Фибоначчи
Стоит отдать должное человеку, который «придумал» эти числа. Леонардо Пизанский. Думаю достаточно, чтобы Вы запомнили имя этого великого человека.
Приступим. Числа Фибоначчи применяются в Теории Чисел. Если сказать честно, я знаю не слишком много об этих числах.
Числа Фибоначчи — это последовательность чисел, в котором каждое последующее числовое значение равно сумме двух предыдущих. Первые два числа Фибоначии — единицы. Соответственно, 3-е число = 2.
Первые 22 числа Фибоначчи:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946.
Еще раз повторюсь — я знаю не слишком много об этих числах. Если я еще не слишком вас утомил/отпугнул/надоел — идем дальше.
Функция Эйлера
В этом пункте я попытаюсь выложить все, что знаю об этом. Я потратил достаточно времени и сил, чтобы изучить эту, между прочим абсолютно простою вещь.
По правде говоря, я очень горжусь тем, что такой человек как Леонард Эйлер жил в России.
К делу. Есть три разных способа посчитать функцию Эйлера. На выбор одного из способов влияют некоторые факторы.
Функция Эйлера обозначается 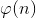 (читать как фи от n).
(читать как фи от n).
Способ №1
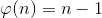
Увы, но этот способ применять следует для высчитывания функции простых чисел.
Например, функция Эйлера для 3 = 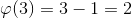
Способ №2
Данный способ следует применять если число можно представить как степень какого-то числа. Например, 9 — это 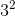
Посчитаем функцию для 9.
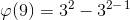
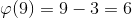
Получаем: 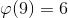
Способ №3
Если число нельзя представить как степень, но можно представить как два множителя — этот способ нам и нужен.
Тут немного сложнее. Нужно разложить число на два множителя, посчитать функцию для каждого из множителей и полученные результаты перемножить.
Также хочу отметить, что если число можно представить и как степень и как два множителя, то в преимуществе всегда степень какого-то числа (о как, в рифму).
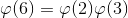
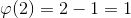
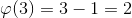
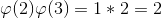
Таким образом получаем: 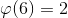
Спасибо за внимание.