Каждый, наверное, сталкивался с задачей расстановки 8 ферзей на шахматной доске.
Рассмотрим решение данной задачи с использованием массива.
Итак, имеем одномерный массив состоящий из 8 элементов. Индексные значения — это строки, а значения в архиве по соответствующим индексам — это столбец шахматной доски соответственно.
Для того, чтобы мы оставили Ферзя в покое и начали перемещать следующего, должны отсутствовать иные Ферзи:
1. по вертикали
2. по диагоналям
3. по горизонтали
Третий пункт в данном методе решения этой задачи можно исключить сразу, так как два Ферзя в одной строке мы изначально не рассматриваем.
На рисунке показано, какие поля попадают под «бой» (Q — устанавливаемый Ферзь, q — поля на которых не должно быть других.)
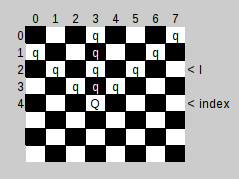
Из чего получаем, что нам необходимо для исключения вертикали сравнить равенство номер столбцов, а для исключения диагоналей сравнить модуль разницы столбцов с разницей строк у устанавливаемого и проверяемого Ферзей.
Вот что мы в итоге получаем:
public class Ferzi2 {
static int[] chessboard = {0,0,0,0,0,0,0,0};
static int index = 0;
static int version = 0;
public static void main(String[] args){
do {
if (checking()){
if (index == 7) {
System.out.println(version++ + " [0]=" + chessboard[0] + " [1]=" + chessboard[1] + " [2]=" + chessboard[2] + " [3]=" + chessboard[3] + " [4]=" + chessboard[4] + " [5]=" + chessboard[5] + " [6]=" + chessboard[6] + " [7]=" + chessboard[7]);
chessboard[index]++;
}
else {
index++;
}
}
else {
chessboard[index]++;
}
} while (chessboard[0]<8);
}
static boolean checking() {
int i;
if (index == 0) {
return true;
}
if (chessboard[index]>7){
chessboard[index] = 0;
index--;
return false;
}
for (i=0;i<index;i++){
if ((chessboard[index] == chessboard[i])|((Math.abs(chessboard[index] - chessboard[i])) == (index-i))){
return false;
}
}
return true;
}
}





![Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс] Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс]](https://www.pvsm.ru/wp-content/plugins/contextual-related-posts/timthumb/timthumb.php?src=http%3A%2F%2Fwww.pvsm.ru%2Fimages%2F2024%2F05%2F10%2Fkak-obhitrit-mozg-i-zastavit-ego-polyubit-slojnye-zadachi-dofaminovyi-detoks-9.jpg&w=100&h=100&zc=1&q=75)
