Функция конкурентного сходства и алгоритм FRiS-СТОЛП

Одной из основных проблем, возникающих при решении задачи классификации каких-либо объектов, является проблема выбора меры схожести. Чаще всего в этой роли выступает расстояние (евклидово, Чебышева, «городских кварталов», и т.п.), однако в некоторых задачах удается добиться более достоверного результата, используя более специфичные меры. В этой статье я хочу немного рассказать о применении т.н. функции конкурентного сходства, или FRiS-функции.

FRiS-функция

FRiS — мера схожести двух объектов относительно некоторого третьего объекта. В отличие от упомянутых ранее классических мер расстояния, эта функция позволяет не просто сказать, похожи объекты друг на друга или нет, но и уточнить ответ на вопрос «по сравнению с чем?». Это позволяет большее количество факторов при классификации.

Пусть дано некоторое множество объектов М с заданной метрикой ρ(a, b). Функция конкурентного сходства объектов a, b ∈ M относительно x ∈ M задается так:

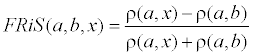
Легко заметить, что значения функции лежат в интервале [–1, 1], причем FRiS(a, a, x) = 1 и FRiS(a, b, a) = –1, В случае же равенства расстояний ρ(a, x) и ρ(b, x) функция примет значение 0.

Пример

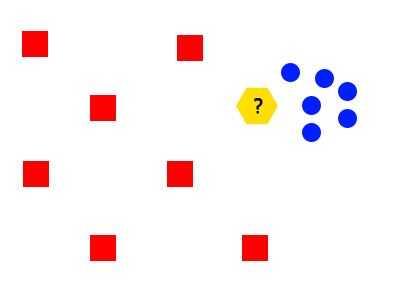
Объекты «красные квадраты» и «синие круги» образуют два класса. Рассматриваемый объект «желтый шестиугольник» располагается ближе к классу «синих кругов», но судя по структуре классов он является типичным представителем «красных квадратов». В большинстве подобных случаев функция конкурентного сходства будет работать корректно.

FRiS-СТОЛП

Другим применением FRiS-функции является один из алгоритмов отбора эталонных образцов для метрического классификатора, именуемый FRiS-СТОЛП. Эталонами здесь называются элементы обучающей выборки X, которые сами образуют обучающую выборку, позволяющую правильно классифицировать само множество X — такая «обучающая выборка в обучающей выборке», набор объектов с наиболее характерными свойствами. В дальнейшем эти эталоны используются в известных алгоритмах классификации, таких как метод ближайших соседей.

Сам алгоритм заключается в следующем. Пусть на входе имеется некоторая обучающая выборка X = {(x_i, c_i )}, где x_i — объекты, а c_i ∈ C — классы, которым они принадлежат (естественно, число классов меньше, чем объектов).

Опишем две вспомогательные функции:

NearestNeighbour(m, M) — возвращает ближайший к m объект из множества M. Реализация близка к очевидной.

FindEtalon(X_с, E) — возвращает новый эталон для класса c исходя из уже имеющихся эталонов E и набора X_с элементов класса c. Для этого для каждого элемента x из X_с вычислим три характеристики:

• Толерантность:
  
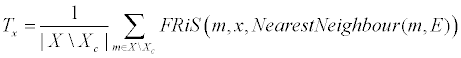
• Обороноспособность:
  
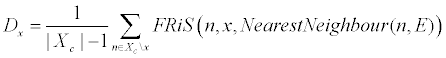
• Эффективность:
  
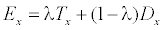
  (параметр λ выбирается из интервала [0, 1] и задает относительный вес характеристик)

Функция FindEtalon(X_с, E) возвращает элемент x из X_с , имеющий максимальную эффективность E_x .

Теперь займемся собственно построением множества эталонов. Для начала проинициализируем начальные множества эталонов для всех классов c ∈ C:

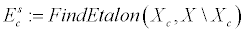
и искомые множества:

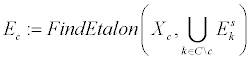
1. Построим множество правильно классифицированных объектов U:

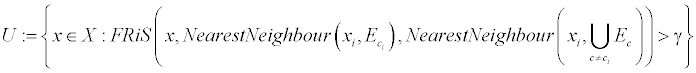
2. Выбросим классифицированные на предыдущем шаге объекты из дальнейшего рассмотрения:


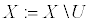
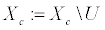
(для всех c ∈ C)

3. Добавим новые эталоны для каждого класса c ∈ C:

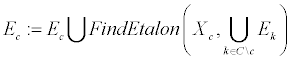
Будем повторять шаги 1–3 до тех пор, пока обучающая выборка X не опустеет либо пока не перестанут появляться новые эталоны. Полученный набор множеств E_с и будет являться искомым набором эталонов, представляющим собой более компактное описание обучающей выборки, исключая из нее неинформативные объекты, удаление которых не скажется на качестве классификации, и выбросы, т.е. объекты одного класса, случайно оказавшиеся внутри другого.

Более подробно с FRiS-функцией можно познакомиться в работе Н.Г. Загоруйко и И.А. Борисовой Функции конкурентного сходства в задаче таксономии / Знания-Онтологии-Теории (ЗОНТ-07).

Автор: r4tz52