Что за распределение у выборочных квантилей?

2024-12-02 в 7:23, admin, рубрики: выборочные квантили, квантили, квантиль, персентиль, перцентиль

Выборочное среднее, выборочная дисперсия, выборочные квантили и прочие статистики – это по своей природе случайные величины. Знание их распределений помогает нам строить более точные доверительные интервалы и проверять статистические гипотезы. И, конечно же, удовлетворять простое любопытство.

Хорошисты курса статистики помнят, что выборочное среднее при некоторых условиях распределено нормально (об этом гласит Центральная предельная теорема). Условия теоремы выполняются для широкого класса распределений, то есть довольно часто, и это очень помогает в повседневных задачах аналитика. Отличники же припоминают кое-что о распределении выборочной дисперсии: при наблюдении n независимых нормально распределенных случайных величин с одинаковыми параметрами, случайная величина $widehatsigma^2 frac{n}{sigma^2}$ (где – выборочная дисперсия и – её оценка) распределена по закону $chi^2_{n-1}$ (хи-квадрат с n-1 степенями свободы; детали этого утверждения приводятся в Теореме Кохрана). Этот факт хоть и менее известен, но всё равно применим при построении доверительных интервалов.

А вот вопрос о выборочных квантилях часто проходит почти незаметно, хотя это тоже широко используемые статистики, и нам бы хотелось строить точные доверительные интервалы и для них. В этой заметке я собрал информацию о распределениях выборочных квантилей и проверил, при каких условиях теоретические выводы работают на практике. Я не буду приводить доказательств, но оставлю код на Python, чтобы при желании можно было повторить эксперименты.

Теорема о распределении выборочных квантилей

В некоторых учебниках можно встретить теорему, которая описывает приближение распределений выборочных квантилей:

Пусть – выборка из распределения с плотностью . Пусть – квантиль уровня , а $z_{n,p}$ – соответствующий выборочный квантиль. Тогда, если непрерывно дифференцируема в окрестности и , то $sqrt{n}(z_p-z_{n,p}) Rightarrow N(0, frac{p(1-p)}{f(z_p)^2})$ .

Другими словами, для определенного класса распределений выборочный квантиль будет распределен примерно нормально с центром в настоящем квантиле и дисперсией $frac{p(1-p)}{f(z_p)^2}$ . Мы будем использовать эту теорему. Я также покажу, при каком можно использовать это приближение.

Распределение на основе порядковых статистик

Следующий вывод основан на том, что, для выборки размером , квантиль уровня примерно равен порядковой статистике $X_{(k)}$ , где .

Если $X_{(k)} leq x$ , то как минимум элементов выборки меньше либо равны . Тогда функция распределения равна:

$F_{X_{(k)}}(x)=sum_{i=k}^n{C_n^kF(x)^i(1-F(x))^{n-i}}$

А соответствующая плотность выражается так:

$f_{X_{(k)}}(x)=frac{n!}{(n-k)!(k-1)!}(1-F(x))^{k-1}F(x)^{n-k}f(x)$

Таким образом, $f_{z_{n,p}}(x) approx f_{X_{([np])}}(x)$ , то есть выборочный квантиль уровня распределен примерно как порядковая статистика уровня , распределение которой мы выписали выше.

Приближение может приводить к проблемам, когда – не целое число, и его необходимо округлить в большую или меньшую сторону. Особенно это заметно, когда дробная часть оказывается равна 0.5, то есть мы теряем больше всего при округлении. Однако даже в этом случае приближение можно использовать на практике.

Также, без дополнительных преобразований такая плотность считается с трудом, потому что и числитель, и знаменатель в дроби растут очень быстро. Уже при , числитель равен примерно $1.3*10^{12}$ .

Какое приближение использовать?

Мы узнали, что в некоторых случаях с ростом размера выборки распределение выборочного квантиля приближается к нормальному, при этом в качестве искомого распределения можно использовать распределение порядковой статистики. Насколько отличны в точности эти два способа в реальных примерах?

Чтобы это понять, я сгенерировал примеры выборочных квантилей для равномерного, экспоненциального и нормального распределений, и сравнил их эмпирические распределения с аппроксимацией нормальным распределением и распределением порядковой статистики. Результаты – ниже.

Равномерное распределение

Сразу отмечу, что приближение нормальным распределением не будет верным для квантилей уровней 0 и 1. Неформально, нормальных распределений с центрами в краях равномерного распределения не получится хотя бы потому, что около этой точки значения будут выбираться только в односторонних окрестностях, то есть оно будет несимметрично. Теорема также не гарантирует приближения, потому что в этих точках плотность распределения не дифференцируема.

Но порядковая статистика $X_{(k)}$ вполне существуют всегда, и случае распределения , распределение можно выразить как бета-распределение: .

Таким образом, выборочный квантиль $z_{n,p}$ для распределения приближенно имеет распределение . А при увеличении и становится верным приближение $z_{n,p} sim N(p, frac{p(1-p)}{n})$ .

Этот вывод можно применить и для случая , если центрировать и нормализовать выборку.

Теперь самое интересное: графики расстояния между двумя способами аппроксимации и эмпирическим распределением. Я использовал метрику Васерштайна (метрика для оценки “расстояния” между распределениями). Чем она меньше – тем ближе друг к другу распределения.

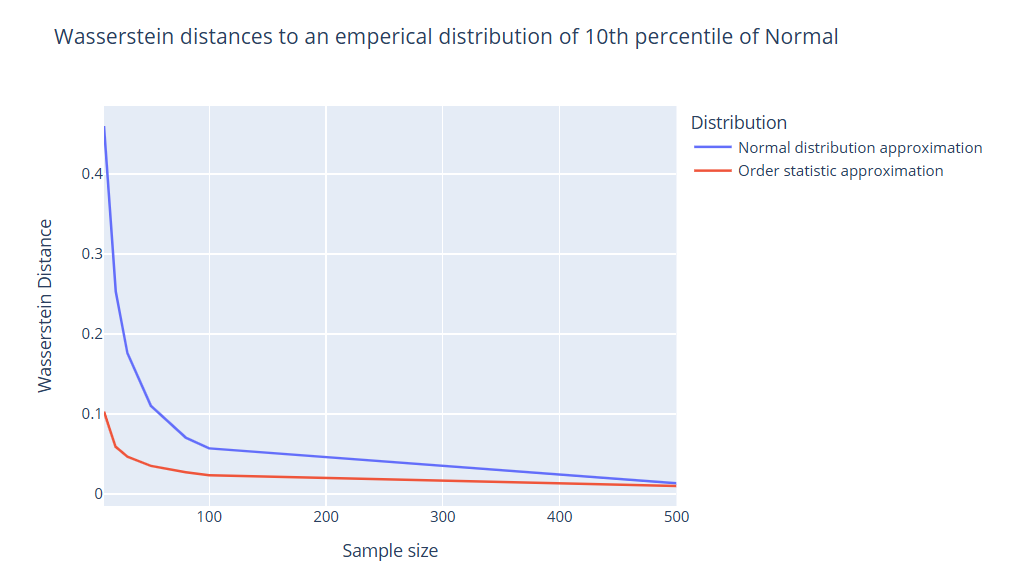
Начнем с квантиля уровня 0.1:

Уже при n=100 разница между нормальным и порядковым приближением невелика — Уже при n = 100 разница между нормальным и порядковым приближением невелика

Можно заметить, что при размерах выборки до 100 распределение, полученное с помощью порядковой статистики, гораздо более точно. А при значениях приближения становятся довольно похожи.

Теперь квантиль уровня 0.5 (медиана):

Медиана приближается нормальным распределением довольно быстро

Теперь нужна гораздо меньшая выборка, чтобы аппроксимация нормальным распределением начала работать – уже при приближения близки друг к другу по качеству.

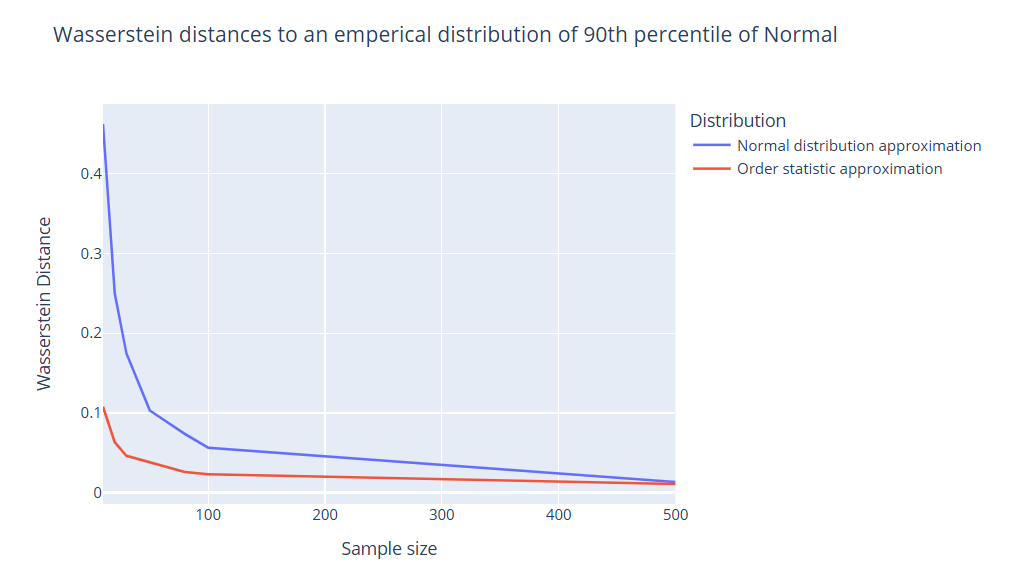
Для квантиля уровня 0.9, квантилей по краям (0.01, 0.99 и подобные), так же как и для оных подальше от медианы, ситуация одинакова – нормальное распределение начинает неплохо приближать распределение квантиля при .

90-ый перцентиль равномерного распределения

Экспоненциальное распределение

Экспоненциальное распределение подходит под условия предельной теоремы для выборочных квантилей во всех точках, кроме 0. Однако порядковая статистика никаким особым способом не выражается, поэтому придется использовать голую формулу из предыдущего раздела.

Результаты очень схожи с тем, что мы видели для равномерного распределения. Если квантиль далек от медианы, приближение нормальным начинает работать при . Медиана же приближается нормальным уже при .

10-ый перцентиль экспоненциального распределения

50-ый перцентиль (медиана) экспоненциального распределения

90-ый перцентиль экспоненциального распределения

Нормальное распределение

Нормальное распределение приближается с помощью теоремы в любой точке. Динамика сходимости для квантилей разных уровней та же, что и с равномерным, и экспоненциальным распределениями.

10-ый перцентиль нормльного распределения

50-ый перцентиль (медиана) нормльного распределения

90-ый перцентиль нормльного распределения

Python-код

Чтобы подсчитать результаты, я для каждого значения размера выборки n из N_LIST генерировал выборку из равномерного/экспоненциального/нормального распределения размера n, получал значение выборочного квантиля для каждого уровня кванитля p из P_LIST, запоминал его и повторял это SAMPLE_SIZE раз. Таким образом, я получал SAMPLE_SIZE квантилей для каждого уровня и каждого размера выборки. Затем я генерировал выборки такого же размера SAMPLE_SIZE из соответствующего нормального распределения и распределения порядковой статистики, и подсчитывал расстояние между ними и реально наблюдаемой выборкой. Я считал такие расстояния AVG_NUM раз, а затем усреднял и сохранял полученное значение. Полный код на Python вы можете найти ниже.

import math

import numpy as np
from scipy.stats import norm, wasserstein_distance


N_LIST = [10, 20, 30, 50, 100, 500]
P_LIST = [0.01, 0.1, 0.25, 0.5, 0.75, 0.9, 0.99]

SAMPLE_SIZE = 1000
AVG_NUM = 30

MU, SIGMA = 1, 2


def norm_order_pdf(x, mu, sigma, n, k):
    tmp_factorial = 1
    for i in range(n, n-k, -1):
        tmp_factorial *= i

    return_val =  tmp_factorial /
    math.factorial(k-1) 
    * norm.cdf(x, loc=mu, scale=sigma)**(k-1) 
    * (1 - norm.cdf(x, loc=mu, scale=sigma))**(n-k) 
    * norm.pdf(x, loc=mu, scale=sigma)

    return return_val


def calc_distances():
    norm_var = norm(MU, SIGMA)
    
    norm_approx_res = {}
    order_approx_res = {}
    
    for p in P_LIST:
        norm_approx_res[p] = {}
        order_approx_res[p] = {}
        for n in N_LIST:
            norm_approx_distances = []
            order_approx_distances = []
            for _ in range(AVG_NUM):
                q_sample = []
                for i in range(SAMPLE_SIZE):
                    norm_sample = norm_var.rvs(size=n)
                    sample_q = np.quantile(norm_sample, p)
                    q_sample.append(sample_q)
                x0 = norm_var.pdf(norm_var.ppf(p))
                norm_approx_distances.append(
                    wasserstein_distance(
                        q_sample, 
                        norm(loc=norm_var.ppf(p), scale=(p * (1-p) / (n * (x0**2))) ** 0.5).rvs(SAMPLE_SIZE)
                    )
                )
                k = round(n * p) + int(p < 0.5)
                x = np.linspace(np.min(q_sample), np.max(q_sample), 50)
                theor_pdf = norm_order_pdf(x, MU, SIGMA, n, k)
                order_sample = np.random.choice(x, p=theor_pdf/theor_pdf.sum(), size=SIGMA)
                order_approx_distances.append(wasserstein_distance(q_sample, order_sample))
            norm_approx_res[p][n] = np.mean(norm_approx_distances)
            order_approx_res[p][n] = np.mean(order_approx_distances)
    return norm_approx_res, order_approx_res


calc_distances()

Выводы

Распределение выборочных статистик можно приближать с помощью распределения соответствующей порядковой статистики или с помощью нормального распределения. Но первое может быть сложнее вычислительно.
При выборках размером приближение с помощью распределения порядковых статистик качественнее, чем нормальное. Однако если квантиль расположен близко к медиане и условия теоремы о выборочных квантилях выполняются, то нормальное распределение приближает распределение выборочного квантиля практически так же хорошо.
При выборках размером нормальное распределение приближает распределение выборочных квантилей любых уровней почти так же хорошо, как и распределение порядковой статистики.
Для равномерного распределения теорема о выборочном квантиле не работает по краям, для экспоненциального – в точке 0. Для других распределений в список “плохих” точек входят точки разрыва плотности вероятности и другие точки, где производной не существует (например, точка 0 у распределения Лапласа).

Теперь вы сможете уверенно строить доверительные интервалы не только для средних, но и для квантилей любых уровней, включая медиану. Возможно, вам понадобится такой навык, и надеюсь, что вам было интресно!

Автор: AntonSoroka

Источник

Информация

Обсуждаемое

Рекомендуем

Что за распределение у выборочных квантилей?

Теорема о распределении выборочных квантилей

Распределение на основе порядковых статистик