Дисклеймер: данная статья является адаптированным переводом. Оригинал можно прочесть здесь.
Байесовские сети при помощи Питона — объяснение с примерами
Из-за ограниченности информации (особенно на родном русском) и ресурсов работы, байесовские сети окружены рядом проблем. И можно было бы спать спокойно, если бы их реализация не осуществлялась в большинстве передовых технологий эры, таких как искусственный интеллект и машинное обучение.
Основываясь на данном факте, эта статья полностью посвящена работе Байесовских сетей и тому, как они сами могут не формировать проблемы, а применяться в их решении, даже если решаемые проблемы крайне запутаны.
Структура статьи
- Что такое Байесовская сеть?
- Что такое направленные ациклические графы?
- Какая математика лежит в Байесовских сетях
- Пример, отражающий идею Байесовской сети
- Суть Байесовской сети
- Байесовская сеть в Питоне
- Применение Байесовских сетей
Погнали.
Что такое Байесовская сеть?
Байесовские сети входят в категорию вероятностных графических моделей (ВГМ). ВГМ используются для вычисления изменчивости для применения в концепциях вероятности.
Общепринятое название Байесовских сетей — Глубокие сети. С их помощью моделируются направленные ациклические графы.
Что такое направленные ациклические графы?
Направленный ациклический граф (как и любой граф в статистике) представляет собой структуру узлов и ссылок, где узлы отвечают за некоторые значения, а ссылки отражают отношения между узлами.
Ациклический == не имеющих направленных циклов. В контексте графов это прилагательное означает, что начиная путь от одной точки, мы пройдем не полностью всю схему графа, а только её часть. (То есть, например если мы начнем с узла 2 на картинке, мы точно не попадем в узел 1).
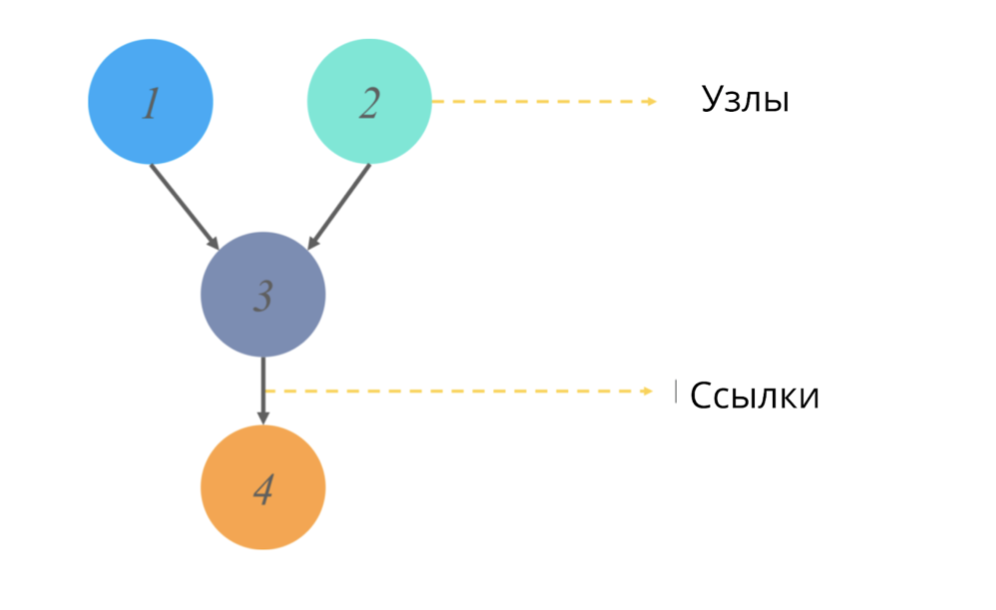
Что же моделируют эти графики и какое выходящее значение дают?
Модели неопределенных направленных графов в том числе базируются на изменении вероятностного происхождения события для каждого из рандомных значений. Для представления и интерпретации каждого значения применима таблица условной вероятности и, таким образом мы можем смоделировать разветвление вероятности последовательно-происходящих событий.
Всё ок. Я тоже сначала запуталась. Для пущего понимания разберем математическую составляющую Байесовских сетей.
Математика Байесовских сетей
Как уже было сказано в определении, Байесовские Сети основываются на теории вероятности, следовательно до начала работы с Байесовскими сетями надо разобраться с двумя вопросами:
Что такое условная вероятность?
Что такое совместное среднее распределение вероятностей?
Условная вероятность
Условная вероятность некоторого Х события — это численное значение вероятности того, что событие Х произойдет при условии, что некоторое событие У уже произошло.
Стандартная формула вероятности для одного значения (не приводится в статье): P(X) = n(x) / N, где n — исследуемые события, а N — все возможные события.
Для двух значений применимы следующие формулы:
Если Х и У зависимые события:
P (X или Y) = P (X ⋂ Y) / P (Y), пересечение вероятность X и У / на вероятность У. (Знак “⋂” в числителе означает пересечение вероятностей)
Если события Х и У независимы:
P(X или Y) = P (X), то есть наступление исследуемых событий равновероятно друг другу.
Совместная вероятность
Совместная вероятность — определение статистической меры для двух или более событий, происходящих единовременно. То есть события Х, У и, допустим С происходят вместе и мы отражаем их совокупную вероятность, используя значение P(X ⋂ У ⋂ С).
Как же это работает в Байесовских сетях? Разберемся на примере.
Пример, отражающий суть Байесовской сети
Допустим, что нам нужно смоделировать вероятность получения одной из градаций оценки студента на экзамене.
Оценка складывается из:
- Уровня сложности экзамена (е): дискретная переменная с двумя градациями (тяжелый, лёгкий)
- IQ студента: дискретная переменная с двумя градациями (низкий, высокий)
Полученное значение оценки будет использоваться в качестве предиктора (предсказательного значения) вероятности поступления студента или студентки в университет.
При этом на допуск к поступлению также будет влиять переменная IQ.
Представим все значения при помощи направленного ациклического графа и таблицы распределения условной вероятности событий.
Используя такое представление, мы сможем рассчитать некоторую совокупную вероятность, формирующуюся из произведения условных вероятностей пяти переменных.
Совокупная вероятность: $inline$p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)$inline$
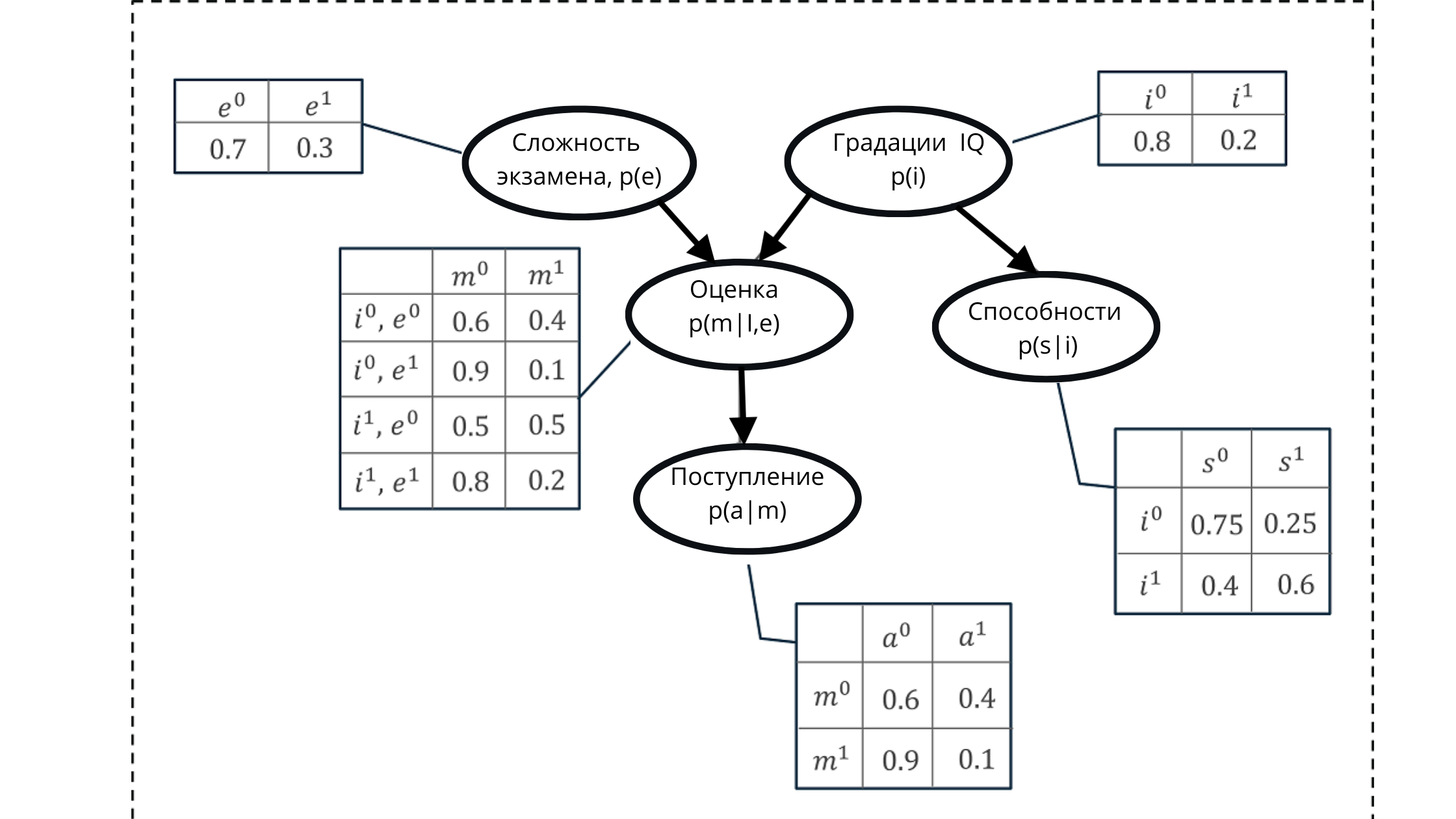
На иллюстрации:
p(e) — распределение вероятностей для градаций переменной экзамен (влияет на оценку p(m|i,e)))
p(i) — распределение вероятностей для градаций переменной IQ (влияет на оценку p(m|i,e)))
p(m |i, e) — распределение вероятности для градаций оценок, базирующаяся на уровне IQ и сложности экзамена (зависит от p(i) и p(e))
p(s| i) — коэффициенты вероятности для способностей студента, базирующиеся на уровне его IQ (зависит от переменной IQ p(i))
p(a | m) — вероятность зачисления студента в университет, базирующаяся на его оценках p(m|i,e)
Здесь напомню, что свойство ациклического графа — отражение взаимосвязи. На рисунке мы четко видим, как родительские узлы влияют на дочерние и как дочерние зависят от родительских.
Отсюда вырисовывается формулировка множества значений, генерируемых при помощи Байесовских сетей.
Суть Байесовской Сети
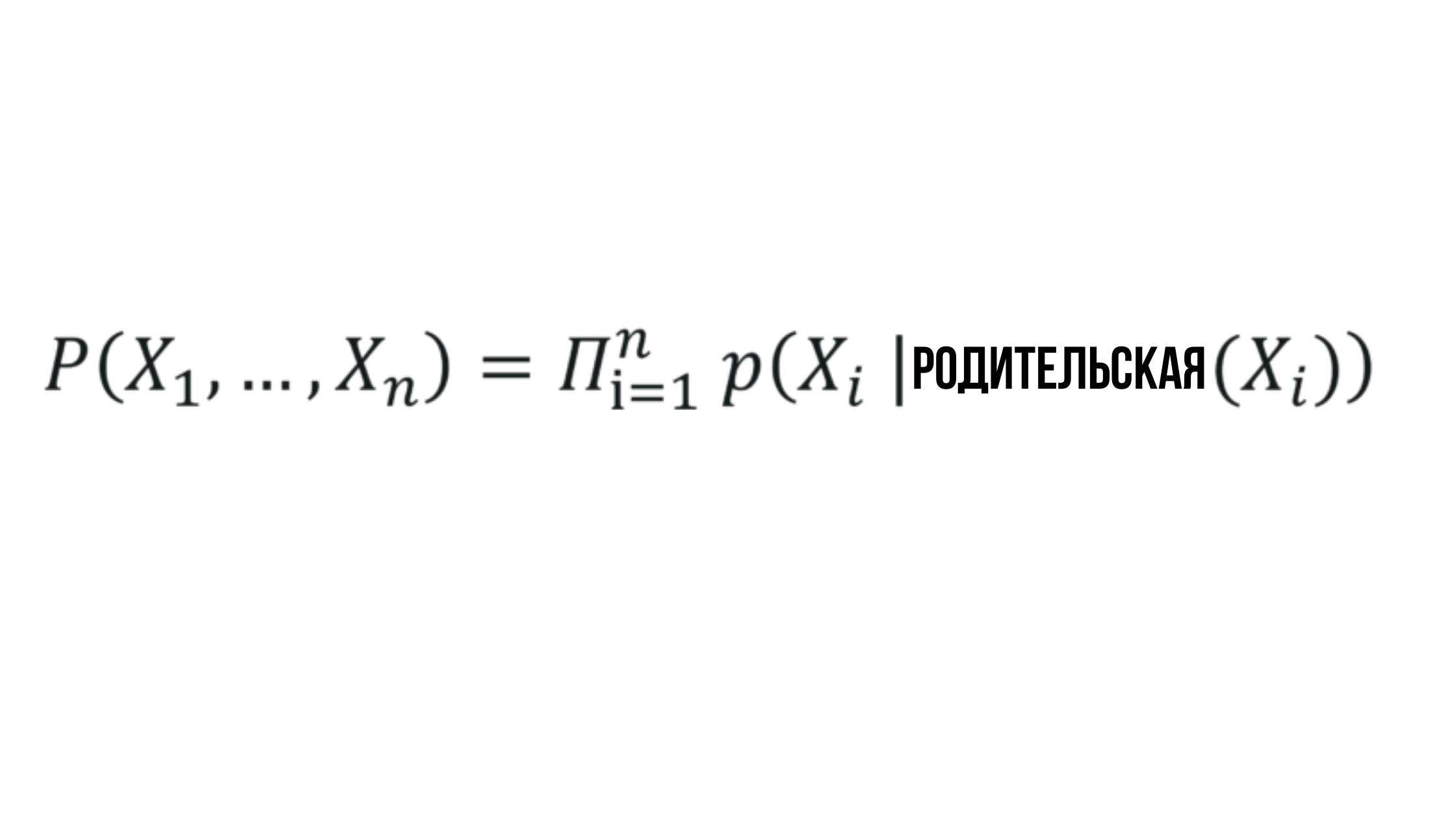
Где вероятность X_i зависит от вероятности соответствующего родительского узла и может быть представлена любым рандомным значением.
Звучит просто и это справедливо — Байесовские сети являются одним из наиболее простых методов, применяемых в описательном (дескриптивном) анализе, прогнозном моделировании и пр.
Байесовская Сеть в Питоне
Давайте рассмотрим применение Байесовской сети к задаче, именуемой “парадокс Монти Холла”.
Суть: представьте, что вы участник апдейт-формата игры “поле Чудес”. Барабан больше не крутиться — теперь вы должны не прилагать свою F, а играть с p.
Перед вами три двери, за которыми равновероятно может расположиться один автомобиль. Двери же, за которыми нет автомобиля приведут вас к козам.
После выбора, ведущий из оставшихся открывает ту, что ведет к козе (например, вы выбрали дверь 1, значит ведущий открывает либо 2, либо 3 дверь) и предлагает вам сменить выбор.
Вопрос: шо делать?
Решение: изначально вероятность выбрать дверь с автомобилем = 33%, а с козой = 66%.
- Если вы попали в 33%, смена двери ведет к проигрышу => вероятность выиграть == 33%
- Если попали в 66% смена ведет к выигрышу => вероятность выиграть == 66%
С точки зрения математической логики, смена двери совокупно в 66% процентах ведет к выигрышу, а в 33% — к проигрышу. Следовательно верная стратегия — менять дверь.
Но мы тут о сети говорим, да и дверей может быть очень много, поэтому переложим решение в модель.
Построим направленный ациклический граф с тремя узлами:
- Дверь с призом (всегда с авто)
- Выбираемая дверь (либо с авто, либо с козой)
- Открываемая дверь в событии 1 (всегда с козой)
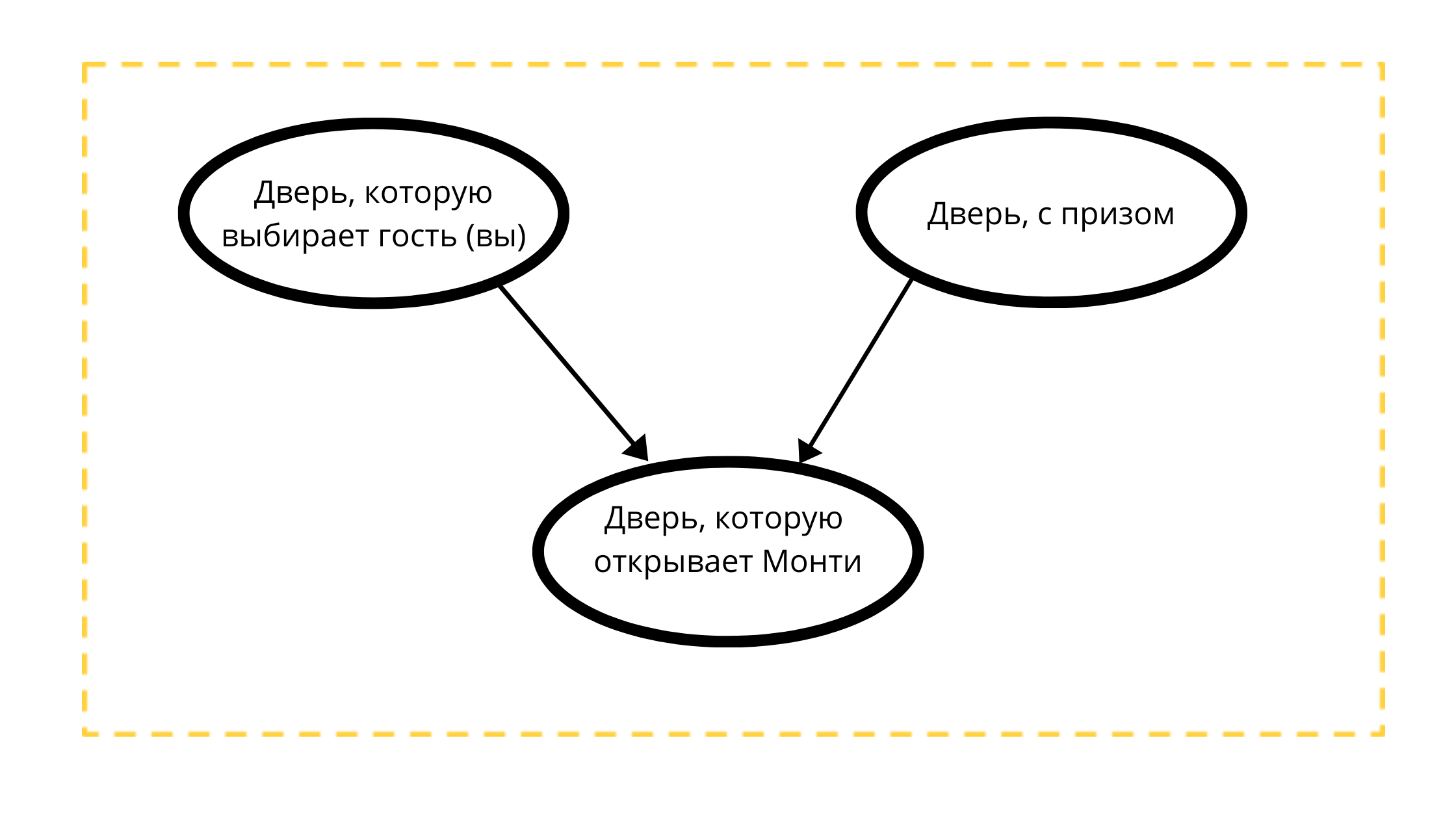
Чтение графа:
На дверь, которую откроет Монти строго влияют две переменные:
- Дверь, выбираемая гостем (вами) тк Монти 100% НЕ откроет ваш выбор
- Дверь с призом, тк Монти всегда открывает непризовую дверь.
По математическим условиям классического примера приз равновероято может быть расположен за любой из дверей, ровно как и вы равновероятно можете выбрать любую дверь.
#Импорт пакетов для работы
import math
from pomegranate import *
# Отражаем вероятность события "Гость выбирает дверь" (равновероятно одну из 3х)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# Отражаем вероятность события "За дверью есть приз" (равновероятно за одной из трёх)
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# Поскольку дверь, которую выберет Монти зависит от двух други, для данной переменной
# строим таблицу распределния вероятностей
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
#Создаём Байесовскую сеть
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()Во фрагменте значения:
- А — дверь, выбранная гостем
- B — призовая дверь
- С — дверь, выбранная Монти
На фрагменте мы рассчитываем значение вероятности для каждого из узлов графа. Два верхних узла подчиняются в нашем примере равному распределению вероятностей, а третий отражает зависимое распределение. Поэтому, чтобы не потерять значения, для С рассчитаны вероятности каждой из возможных комбинаций игры.
Подготовив данные, создаём Байесовскую сеть.
Здесь важно отметить, что одно из свойств такой сети — выявления влияния скрытых переменных на наблюдаемые. При этом ни скрытые, ни наблюдаемые переменные не нужно указывать или определять заранее — модель сама исследует влияние скрытых переменных и сделает это тем точнее, чем больше получаемых ею переменных.
Приступаем к предсказаниям.
beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}Разберем фрагмент на примере переменной А.
Допустим, гость выбрал её (А).
Событие “за дверью есть приз” на этапе выбора двери гостем имеет распределение вероятностей == ⅓ (тк каждая дверь равновероятно можем быть призовой).
Далее добавим значение вероятностей двери быть призовой на этапе, когда дверь выбирает Монти. Поскольку мы не знаем, призовую ли дверь исключили собственным (гостевым) выбором на шаге 1, вероятность двери быть призовой на данном этапе распределиться 50/50
beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B
На этом этапе мы модифицируем входные значения для нашей сети. Теперь она работает с распределением вероятностей, полученным на шагах 1 и 2, где
- шансы быть призовой у двери, выбранной нами, не изменились (33%)
- шансы быть призовой у двери, которую открыл Монти (В) аннулировались
- шансы быть призовой у двери, которая осталась без внимания приняли значение 66%
Следовательно, как и было заключено выше, верной стратегией со стороны гостям для данной игры является смена двери — те, кто поменяет дверь математически имеют ⅔ шансов на победу против тех, кто дверь не сменит (⅓).
В примере с тремя узлами, несомненно, хватает расчетов вручную, но при увеличении числа переменных, узлов и факторов влияния — Байесовская сеть способна решить задачу прогностического значения.
Применение Байесовских сетей
1. Диагностика:
- предсказание наличия болезни на основе симптоматики
- моделирование симптоматики для исходной болезни
2. Поиск в Сети интернет:
- формирование выдачи на основе анализа пользовательского контекста (намерений)
3. Классификация документов:
- спам-фильтры на основе анализа контекста
- распределение документации по категориям/классам
4. Генная инженерия
- моделирование поведения сетей регуляции генов на основе взаимосвязей и взаимоотношений сегментов ДНК
5. Фармацевтика:
- мониторинг и прогностическое значение допустимых доз
Изложенные выше примеры — факты. Для полнного понимания релевантно попредставлять, на каком этапе подключается создание Байесовской сети и из каких узлов состоит граф, её описывающий.
Задача о парадоксе Монти Холла — лишь фундамент, который позволяет “на пальцах” проиллюстрировать работу цепей, основанных на комбинации зависимого и независимого распределения вероятностей. Надеюсь, у меня это получилось.
P.S. я не являюсь асом Питона и только учусь, поэтому не могу отвечать за код автора. Публикация данной статьи на Хабре преследует больше выпуск в мир интеллектуального труда перевода. Думаю, в будущем смогу и генерировать собственные туториалы — в них уже буду рада видеть конструктивные мысли насчет кода.
Автор: Сабрина