Главная

Как IndVarSimplification применяет математику в вашем коде

2023-05-29 в 11:02, admin, рубрики: induction variable, llvm optimization, Rust, scalar evolution, оптимизация

Хочу поделиться своей историей расследования одной довольно необычной компиляторной оптимизации. Необычна она в том плане, что для нее производятся довольно нетривиальные математические вычисления. Приступим!

Чем я пользовался

Есть такой замечательный сайт: Compiler Explorer. Туда можно вставить код на одном из многих популярных языков программирования и посмотреть на ассемблер, в который этот код компилируется. Помимо ассемблера можно увидеть и другую полезную информацию, например промежуточные представления кода в процессе компиляции, а также список применяемых LLVM оптимизаций.

Рассмотрим вот такой простой код на языке Rust:

pub fn fancy_function(n: u64) -> u64 {
    let mut sum = 0;
    for i in 0..n {
        sum += i;
    }
    sum
}

Даже люди, не знакомые с Rust, смогут понять, что тут происходит: заводим переменную sum, проходим циклом по числам от до и суммируем их. Сумма возвращается из функции.

Казалось бы, как это можно упростить? Давайте заглянем в ассемблер:

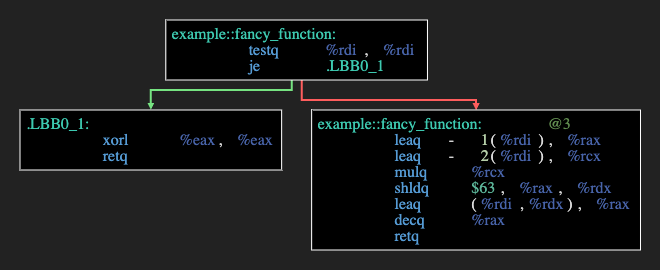
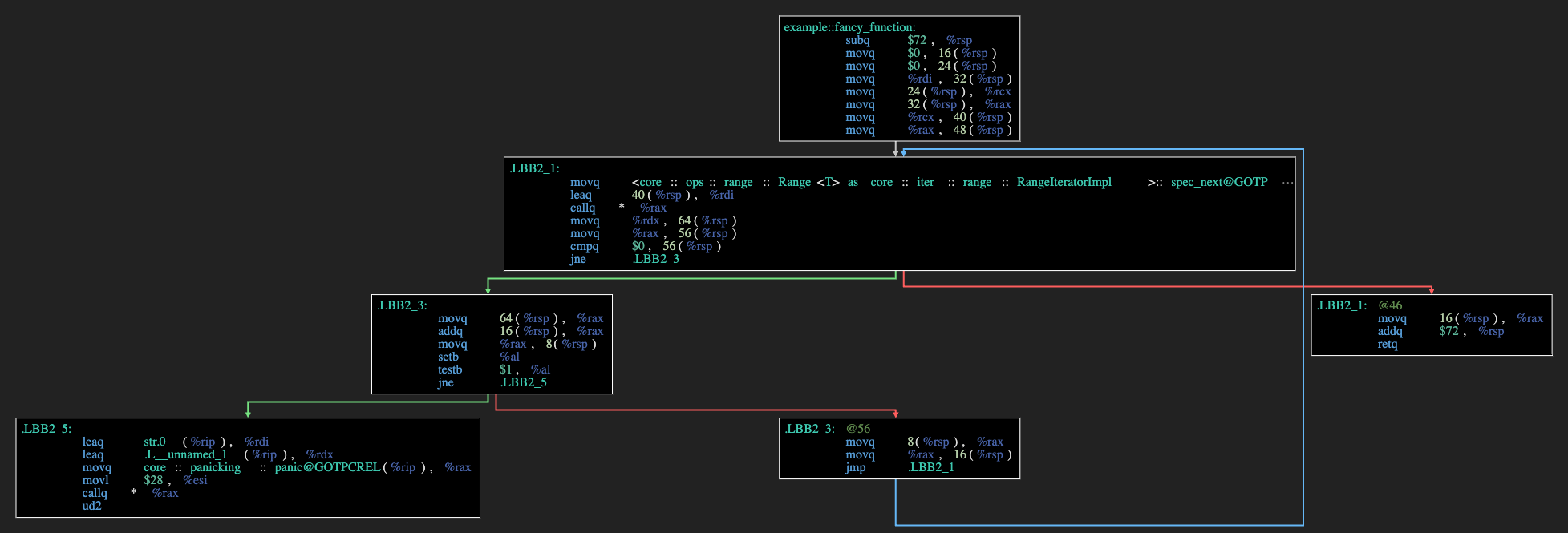
Я нарисовал это в виде графа условных переходов. Зеленая ветка - если переход произошел, красная - если нет.

Самое интересное тут в том, что в ассемблере нет циклов вообще. Как же тогда он делает вычисления? Разобрав правую ветку, я вспомнил школьную математику, а именно, что:

$1 + 2 + dots + (n - 1)=frac{n(n - 1)}{2}$

Да, действительно, по такой формуле все и считается. Это выглядит очень любопытно, давайте посчитаем более сложную сумму:

pub fn fancy_function(n: u64) -> u64 {
    let mut sum = 0;
    for i in 0..n {
        sum += i * i * i + 2 * i * i + 3 * i + 42;
    }
    sum
}

Здесь мы считаем сумму многочленов 3 степени. Кажется, я вспоминаю, как нам в универе рассказывали, что сумму любых многочленов можно выразить в виде формулы от n. Выведет ли эту формулу компилятор?

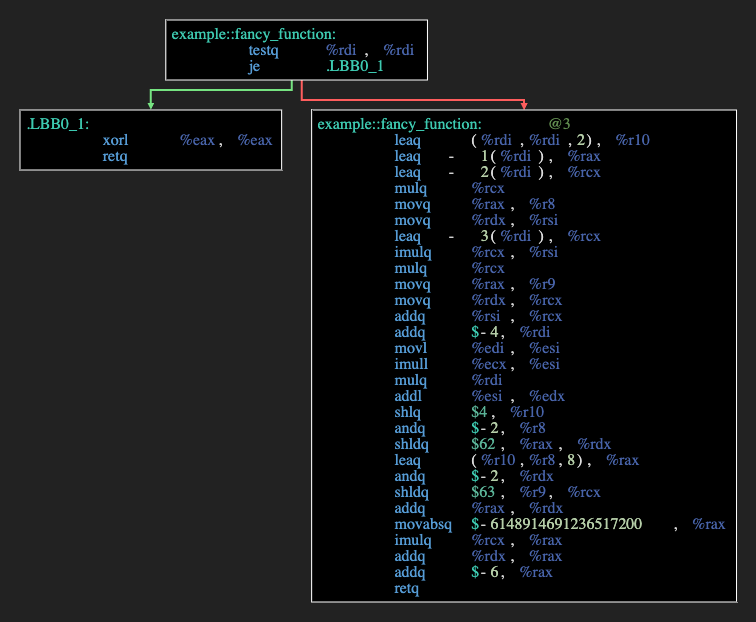
Да, это произошло! Формула конечно гораздо сложнее, чем в первом случае, но это все еще формула, которая считается за .

На этом моменте мне захотелось разобраться, кто, в какой момент и каким образом проводит эту замечательную оптимизацию, и я начал с описания процесса компиляции Rust. Если вкратце, то код на языке Rust оптимизируется в двух местах:

Mid-level Intermediate Representation (MIR) - представление кода, в котором убран весь синтаксический сахар и выведены типы всех объектов. На данном этапе применяются оптимизации, специфичные для языка Rust.
LLVM Intermediate Representation (LLVM-IR) - формат кода, который передается в LLVM для последующей компиляции в бинарный файл. Здесь применяются оптимизации LLVM.

Попробуем отключить оптимизации MIR. Для этого выберем nightly версию компилятора Rust и посмотрим. Для простоты я вернулся к первому примеру с суммой от до

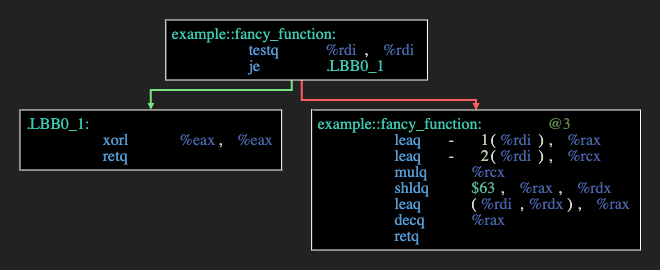
А теперь наоборот, включим оптимизации MIR и выключим оптимизации LLVM:

Видите голубую стрелочку наверх? Это цикл! И даже в ассемблере больше нет инструкций умножения чисел, только сложения. Выходит это оптимизация на уровне LLVM? Давайте проверим.

В Compiler Explorer можно вывести список всех примененных оптимизаций, и среди них я нашел такую:

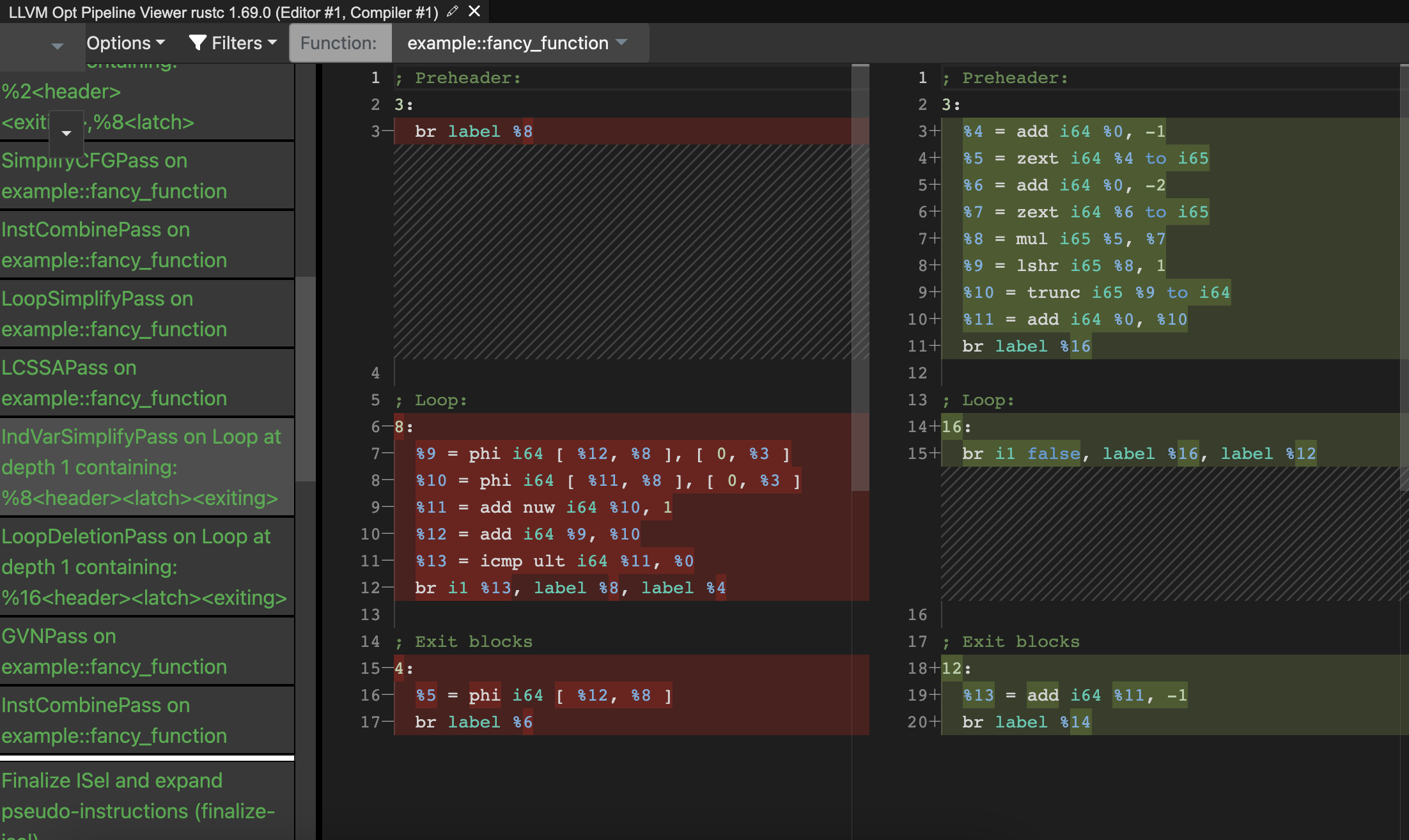
Оптимизация называется IndVarSimplifyPass. Тут было удалено тело цикла и вынесено в виде формулы . А то, что осталось от цикла, будет удалено позже другими оптимизациями.

Беглым взглядом пробежавшись по исходному коду IndVarSimplifyPass, я нашел комментарий о том, что вся "магия" происходит с помощью Scalar Evolution Evaluation.

Перед тем, как читать его исходный код, я посмотрел видео на YouTube от LLVM, где разбирается SCEV Evaluation, и вкратце объясняется, какая математика за этим стоит.

Если вкратце, то бывают простые рекуррентные последовательности, записывающиеся в нотации :

То есть это обычная арифметическая прогрессия. Можно подняться на уровень выше и получить более сложную:

То есть начинаем с элемента , а затем на каждом шаге прибавляем элементы арифметической прогрессии . Можно аналогично определять последовательности больших порядков.

В данной нотации можно выразить сумму i-го элемента:

${x_1, +, x_2, +, dots, +, x_n}_i=x_1 binom{i}{0} + x_2 binom{i}{1} + ldots + x_n binom{i}{n - 1}$

А сумму можно выразить так:

$sum_{i=1}^n {x_1, +, dots, +, x_n}={0, +, x_1, +, dots, +, x_n}_n$

А еще есть правила, по которым такие последовательности можно поэлементно складывать и умножать.

И вот, проглядев код SCEV Evaluation, я нашел места, где происходят математические вычисления:

Тут вычисляются биномиальные коэффициенты
Тут считается i-й элемент последовательности
Тут считается сумма двух последовательностей
А тут вычисляется произведение последовательностей.

Чтобы окончательно разобраться в этом, я написал простой парсер выражений, в который вводится формула i-го элемента (в виде полинома от i), и выводится формула суммы этих элементов при i от 0 до Пример:

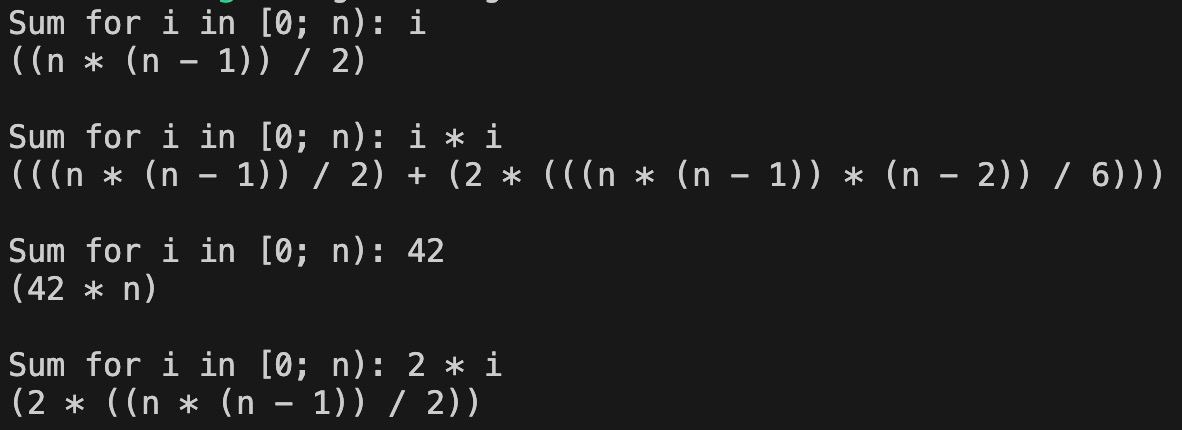
Посмотреть код и попробовать можно в моем репозитории.

В заключение, хочу выразить мысль, что такая оптимизация в очередной раз подчёркивает, что код, который вы написали, не обязательно будет совпадать в точности с тем, что будет исполнять процессор.

Автор: Тагир Хамитов

Источник