Сканирующее окно по массивам NumPy

CoLab блокнот с примерами

Возможно сделать скользящее окно (rolling window, sliding window, moving window) по массивам NumPy на языке программирования Python без явных циклов. В данной статье рассматривается создание одно-, двух-, трех- и N-мерных скользящих окон по массивам NumPy. В результате скорость обработки данных увеличивается в несколько тысяч раз и сравнима по скорости с языком программирования С.

Cкользящее окно применяется в: обработке изображений, искусственных нейронных сетях, интернет протоколе TCP, обработке геномных данных, прогнозировании временных рядов и т.д.

Отказ от ответственности: в исходном коде могут быть ошибки! Если вы видите ошибку, пожалуйста, напишите мне.

• Введение
• Скользящее 1D окно по ND массиву в Numpy
• Скользящее 2D окно по ND массиву в Numpy
• Скользящее 3D окно по ND массиву в Numpy
• Скользящее MD окно по ND массиву, где M ≤ N
• Скользящее MD окно по ND массиву для любых M и N

---

Введение

Эта статья является продолжением моего ответа на сайте StackOverflow. Мои первые эксперименты со скользящим окном здесь и здесь.

Практическая реализация скользящего двумерного окна по двумерному массиву изображения находится в функции roll файла logic_tools.py проекта Ручная разметка изображений с помощью многоугольников.

Алгоритмы для одномерного скользящего окна уже реализованы здесь, здесь и здесь.

Для понимания темы, вам необходимо знать, что такое страйды (strides, шаги).

Какое-то скользящее окно реализовано в библиотеке Pandas, однако автор плохо знаком с библиотекой Pandas, чтобы сказать, насколько универсальная и быстрая приведенная там реализация. К тому же всегда интереснее сделать функционал самому, если есть такая возможность. Как альтернативу, можно задействовать библиотеку Cython, однако скорость обработки все-равно будет ниже, чем в NumPy.

---

1. Скользящее 1D окно по ND массиву в Numpy

Простейшее одномерное скользящее окно по многомерному массиву выглядит так:

# Rolling 1D window for ND array
def roll(a,      # ND array
         b,      # rolling 1D window array
         dx=1):  # step size (horizontal)
    shape = a.shape[:-1] + (int((a.shape[-1] - b.shape[-1]) / dx) + 1,) + b.shape
    strides = a.strides[:-1] + (a.strides[-1] * dx,) + a.strides[-1:]
    return np.lib.stride_tricks.as_strided(a, shape=shape, strides=strides)

Функция numpy.lib.stride_tricks.as_strided создает новый вид (view) массива с заданной формой (shape) и шагами (strides).

Форма (shape) нового массива создается из формы входного многомерного массива, по которому осуществляется движение сканирующего окна, и формы одномерного сканирующего окна. Тогда как шаги (strides) создаются только из шагов входного многомерного массива без участия одномерного сканирующего окна.

Форма (shape) состоит из трех слагаемых:

• a.shape[:-1] — это остаток от формы ND-массива, где N > 1. Если N == 1, то этот остаток будет равен пустому кортежу t == (), таким образом это слагаемое не важно для N == 1.
• (int((a.shape[-1] - b.shape[-1]) / dx) + 1,) — это количество шагов скользящего окна по последней размерности [-1] массива. Шаг сканирующего окна dx может быть равным: 1, 2, 3 и т.д.
• b.shape — это форма скользящего окна.

Шаги (strides) также состоят из трех сладаемых:

• a.strides[:-1] — это остаток от шагов ND-массива, где N > 1. Если N == 1, то этот остаток будет равен пустому кортежу t == (), таким образом это слагаемое не важно для N == 1.
• (a.strides[-1] * dx,) — это количество байт между шагами скользящего окна. Например, целочисленный int массив имеет 4 байта в одном шаге между соседними элементами, таким образом для шага dx == 2 шаг в байтах составит 4 * 2 = 8 байт.
• a.strides[-1:] — это шаг в байтах между соседними элементами. Например, целочисленный int массив имеет шаг 4 байта между соседними элементами, тогда данный кортеж равен (4,).

---

2. Скользящее 2D окно по ND массиву в Numpy

Примеры скользящего 2D окна по 2D массиву:

• найти меньшее изображение в большем;
• сделать операцию свертки в искусственной нейронной сети;
• применить цифровой фильтр к изображению (фильтры Собеля, Гауссиан, размытия и т.д.).

В общем, скользящее 2D окно позволяет проводить периодические операции на матрице с каким-либо шагом. Операции сравнения, свертки, вычитания, умножения, применения цифрового фильтра и т.д. Здесь так же, как в разделе один, создается вид нового массива с помощью формы и шагов.

# Rolling 2D window for ND array
def roll(a,      # ND array
         b,      # rolling 2D window array
         dx=1,   # horizontal step, abscissa, number of columns
         dy=1):  # vertical step, ordinate, number of rows
    shape = a.shape[:-2] + 
            ((a.shape[-2] - b.shape[-2]) // dy + 1,) + 
            ((a.shape[-1] - b.shape[-1]) // dx + 1,) + 
            b.shape  # sausage-like shape with 2D cross-section
    strides = a.strides[:-2] + 
              (a.strides[-2] * dy,) + 
              (a.strides[-1] * dx,) + 
              a.strides[-2:]
    return np.lib.stride_tricks.as_strided(a, shape=shape, strides=strides)

Форма состоит из четырех слагаемых: три слагаемых такие же, как в разделе один, а четвертое слагаемое — это количество вертикальных шагов скользящего окна ((a.shape[-2] - b.shape[-2]) // dy + 1,). Выражение:

    (int((a.shape[-1] - b.shape[-1]) / dx) + 1,)

было заменено на

    ((a.shape[-1] - b.shape[-1]) // dx + 1,)

потому что эти два выражения эквивалентны.

Шаги (страйды) также похожи на раздел один, но с дополнительным страйдом (a.strides[-2] * dy,) для вертикального шага скользящего 2D окна.

Функция для проверки результатов выводит в консоль количество найденных совпадений counts, их координаты coords и выглядит следующим образом:

def show_results(a, b, dx=1, dy=1):
    axis = a.ndim  # number of dimensions
    # np.all over 2 dimensions of the rolling 2D window
    bool_array = np.all(np.all(
            roll(a, b, dx, dy) == b,
        axis=axis),axis=axis)
    counts = np.count_nonzero(bool_array)
    coords = np.transpose(np.nonzero(bool_array)) * [dy, dx]
    print("Found {counts} elements with coordinates:n{coords}".format(
        counts=counts, coords=coords))

Здесь np.all применяется к двум размерностям 2D скользящего окна. Для получения правильных координат совпадения coords результат домножается на вертикальный и горизонтальный шаги [dy, dx] скользящего окна.

---

3. Скользящее 3D окно по ND массиву в Numpy

Можно увидеть шаблон (паттерн) для одно- и двумерных скользящих окон. Сложно понимать работу алгоритма в более высоких размерностях, однако можно воспользоваться замеченным шаблоном для реализации скользящего 3D окна по ND-мерному массиву.

Пример скользящего 3D окна по 3D массиву — это различные операции с вокселами (трехмерными пикселами) в трехмерных изображениях. В тестовом CoLab примере ищутся обычные совпадения малого 3D под-массива в большем, однако можно придумать и более сложные операции (свертка, цифровые фильтры, сравнения и т.д.).

# Rolling 3D window for ND array
def roll(a,      # ND array
         b,      # rolling 2D window array
         dx=1,   # horizontal step, abscissa, number of columns
         dy=1,   # vertical step, ordinate, number of rows
         dz=1):  # transverse step, applicate, number of layers
    shape = a.shape[:-3] + 
            ((a.shape[-3] - b.shape[-3]) // dz + 1,) + 
            ((a.shape[-2] - b.shape[-2]) // dy + 1,) + 
            ((a.shape[-1] - b.shape[-1]) // dx + 1,) + 
            b.shape  # multidimensional "sausage" with 3D cross-section
    strides = a.strides[:-3] + 
              (a.strides[-3] * dz,) + 
              (a.strides[-2] * dy,) + 
              (a.strides[-1] * dx,) + 
              a.strides[-3:]
    #print('shape =', shape, " strides =", strides)  # for debugging
    return np.lib.stride_tricks.as_strided(a, shape=shape, strides=strides)

Для нахождения количества совпадений counts и координат этих совпадений coords применяется следующая функция:

def show_results(a, b, dx=1, dy=1, dz=1):
    axis = a.ndim  # number of dimensions == 3
    # np.all over 3 dimensions of the rolling 3D window
    bool_array = np.all(np.all(np.all(
            roll(a, b, dx, dy, dz) == b,
        axis=axis), axis=axis), axis=axis)
    counts = np.count_nonzero(bool_array)
    coords = np.transpose(np.nonzero(bool_array)) * [dz, dy, dx]
    print("Found {counts} elements with coordinates:n{coords}".format(
        counts=counts, coords=coords))

---

4. Скользящее MD окно по ND массиву, где M ≤ N

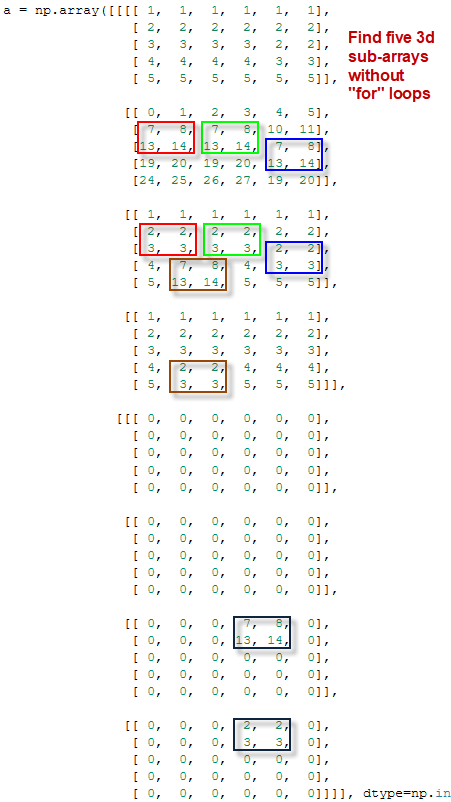
Обобщим функции roll и show_results на многомерное скользящее MD окно по ND массиву, где размерность M скользящего окна меньше либо равна размерности N исходного массива: M ≤ N.

# Rolling MD window for ND array
def roll(a,        # ND array
         b,        # rolling MD window array
         d=None):  # steps array

    # Make several verifications
    n = a.ndim  # array dimensions
    m = b.ndim  # rolling window dimensions
    if m > n:  # check if M ≤ N
        print("Error: rolling window dimensions is larger than the array dims")
        return None
    if d is None:  # steps are equal to 1 by default
        d = np.ones(m, dtype=np.uint32)
    elif d.ndim != 1 and d.size != m:
        print("Error: steps number must be equal to rolling window dimensions")
        return None
    elif not np.issubdtype(d.dtype, np.integer) or 
         not (d > 0).all():
        print("Error: steps must be integer and > 0")
        return None

    s = np.flip(d)  # flip the 1D array of step sizes
    sub = np.subtract(a.shape[-m:], b.shape[-m:])
    steps = tuple(np.divide(sub, s).astype(np.uint32) + 1)
    shape = a.shape[:-m] + steps + b.shape

    section = tuple(np.multiply(a.strides[-m:], s))
    strides = a.strides[:-m] + section + a.strides[-m:]

    #print('shape =', shape, " strides =", strides)  # for debugging
    return np.lib.stride_tricks.as_strided(a, shape=shape, strides=strides)

Вначале функции roll находится тривиальная проверочная часть для массива шагов скользящего окна. Нетривиальные части следующие:

• steps = tuple(np.divide(sub, s).astype(np.uint32) + 1) — вычисление количества шагов скользящего окна по многомерному массиву.
• section = tuple(np.multiply(a.strides[-m:], s)) — рассчет секции (вставки) для страйдов «многомерной сосиски».
• Создание «многомерной сосиски» путем вставки section в ND-массив: strides = a.strides[:-m] + section + a.strides[-m:].

Функция нахождения количества совпадений counts и координат этих совпадений coords выглядит следующим образом:

def show_results(a, b, d=None):
    n = a.ndim  # array number of dimensions == N
    m = b.ndim  # rolling window dimensions == M
    if d is None:  # step sizes are equal to 1 by default
        d = np.ones(m, dtype=np.uint32)
    bool_array = roll(a, b, d) == b
    # np.all over M dimensions of the rolling MD window
    for i in range(m):
        bool_array = np.all(bool_array, axis=n)
    counts = np.count_nonzero(bool_array)
    # flip 1D array of step sizes and concatenate it with remaining dimensions
    s = np.concatenate((np.ones(n-m, dtype=int), np.flip(d)))
    coords = np.transpose(np.nonzero(bool_array)) * s
    print("Found {counts} elements with coordinates:n{coords}".format(
        counts=counts, coords=coords))

Нетривиальные части функции show_results следующие:

• Создание логического (двоичного) массива bool_array или маски для найденных совпадений. Затем применение numpy.all ко всем m размерностям для проверки, все ли элементы массива в данном измерении имеют значение True. Обратите внимание, что bool_array — это ND массив и он имеет axis=n, но np.all применяется m раз по всем размерностям скользящего MD окна:

    bool_array = roll(a, b, d) == b
    # np.all over M dimensions of the rolling MD window
    for i in range(m):
        bool_array = np.all(bool_array, axis=n)

• Еще одна нетривиальная часть для M < N. Если M < N мы должны не только перевернуть одномерный 1D массив шагов скользящего окна, но и объединить его с одномерным массивом из единиц для оставшихся размерностей N-M (шаг по высшим размерностям равен 1). Если M == N, то оставшиеся размерности равны нулю, и в этом случае конкатенация не требуется:

  # flip 1D array of step sizes and concatenate it with remaining dimensions
  s = np.concatenate((np.ones(n-m, dtype=int), np.flip(d)))

---

5. Скользящее MD окно по ND массиву для любых M и N

Возможно ли сделать скользящее MD окно по ND массиву, где M > N? В общем, да! Однако только часть скользящего окна будет пересекаться с ND массивом, потому что у скользящего MD окна будет больше размерностей M > N.

Давайте найдем совпадения между пересечениями MD и ND массивов. И реализуем скользящее MD окно по ND массиву для любых M и N. Для этого используем предыдущие функции roll и show_results.

def get_results(a, b, d=None):  # the same as `show_results` function
    n = a.ndim  # array number of dimensions == N
    m = b.ndim  # rolling window dimensions == M
    if d is None:  # step sizes are equal to 1 by default
        d = np.ones(m, dtype=np.uint32)
    bool_array = roll(a, b, d) == b
    # np.all over M dimensions of the rolling MD window
    for i in range(m):
        bool_array = np.all(bool_array, axis=n)
    counts = np.count_nonzero(bool_array)
    # flip 1D array of step sizes and concatenate it with remaining dimensions
    s = np.concatenate((np.ones(n-m, dtype=int), np.flip(d)))
    coords = np.transpose(np.nonzero(bool_array)) * s
    return (counts, coords)

def show_intersections(a, b, d=None):
    d_tmp = d
    n = a.ndim  # array number of dimensions == N
    m = b.ndim  # rolling window dimensions == M
    #
    if d_tmp is None:  # step sizes are equal to 1 by default
        d_tmp = np.ones(m, dtype=np.uint32)
    elif m > n and d_tmp.size == n:  # for m > n case
        # Concatenate d_tmp with remaining dimensions
        d_tmp = np.concatenate((np.ones(m-n, dtype=int), d_tmp))
    #
    counts = 0
    coords = None
    if m <= n:
        results = get_results(a, b, d_tmp)  # return previous example
        counts = results[0]
        coords = results[1]
    else:  # if m > n
        t = m - n  # excessive dimensions
        layers = np.prod(b.shape[:t])  # find number of layers
        # Reshape MD array into (N+1)D array.
        temp = b.reshape((layers,) + b.shape[t:])
        # Get results for every layer in the intersection
        for i in range(layers):
            results = get_results(a, temp[i], d_tmp[t:])
            counts += results[0]
            if coords is None:
                coords = results[1]
            else:
                coords = np.concatenate((coords, results[1]))
    print("Found {counts} elements with coordinates:n{coords}".format(
        counts=counts, coords=coords))

Функция get_results та же самая, что и show_results с небольшими изменениями в выводе результата.

Функция show_intersections получает пересечения между многомерными массивами. Если M <= N, то функция show_intersections просто возвращает функцию get_results, как в предыдущем разделе. Если M > N, то мы должны найти пересечение между массивами b и a.

Для этого найдем количество излишних размерностей t = m - n между MD массивом b и ND массивом a. И найдем количество слоев в пересечении между b и a: layers = np.prod(b.shape[:t]). Затем переформируем (придадим иную форму, reshape) массив b из MD массива в (N+1)D массив:

    # Reshape MD array into (N+1)D array.
    temp = b.reshape((layers,) + b.shape[t:])

Наконец найдем результат: совпадения между двумя массивами (N+1)D и ND, где размерность (N+1) имеет количество слоев равное layers:

    # Get results for every layer in the intersection
    for i in range(layers):
        results = get_results(a, temp[i], d_tmp[t:])

Объединим количество совпадений counts и найдынных координат этих совпадений coords для каждого слоя:

    # Get results for every layer in the intersection
    for i in range(layers):
        results = get_results(a, temp[i], d_tmp[t:])
        counts += results[0]
        if coords is None:
            coords = results[1]
        else:
            coords = np.concatenate((coords, results[1]))

Все примеры находятся в CoLab блокноте.

Спасибо за внимание!

Автор: FooBar167

Источник