Точность глубины — это боль в заднице, с которой рано или поздно сталкивается любой программист графики. На эту тему написано множество статей и работ. А в разных играх и движках, и на различных платформах можно увидеть множество различных форматов и настроек depth buffer.
Преобразование глубины на GPU выглядит неочевидным из-за того, как именно оно взаимодействует с перспективной проекцией, и изучение уравнений ситуацию не проясняет. Чтобы понять как это работает, полезно нарисовать несколько картинок.
Эта статья разделена на 3 части:
- Я попытаюсь объяснить мотивацию нелинейного преобразования глубины.
- Я представлю несколько графиков, которые помогут понять как нелинейное преобразование глубины работает в разных ситуациях, интуитивно и визуально.
- Обсуждение основных выводов Tightening the Precision of Perspective Rendering [Paul Upchurch, Mathieu Desbrun (2012)], касающихся влияния ошибки округления чисел с плавающей точкой на точность глубины.
Почему 1/z?
Аппаратный GPU depth buffer обычно не хранит линейное представление расстояния между объектом и камерой, вопреки тому, что от него при первой встрече наивно ожидают. Вместо этого, depth buffer хранит значения, обратно пропорциональные view-space глубине. Я хочу кратко описать мотивацию такого решения.
В этой статье я буду использовать d для представления значений, хранимых в depth buffer (в диапазоне [0, 1] для DirectX), и z для представления view-space глубины, т.е. реальное расстояние от камеры, в мировых единицах измерения, например метры. В общем случае отношение между ними имеет следующий вид:

где a,b — это константы, связанные с настройками near и far плоскостями. Другими словами d — это всегда некоторое линейное преобразование от 1/z.
На первый взгляд может показаться, что в качестве d можно взять любую функцию от z. Так почему она выглядит именно так? На это есть две основные причины.
Во-первых, 1/z естественно вписывается в рамки перспективной проекции. А это самый основной класс преобразований, который гарантированно сохраняет прямые. Поэтому перспективная проекция подходит для аппаратной растеризации, поскольку прямые ребра треугольников остаются прямыми на экране. Мы можем получить линейное преобразование от 1/z, используя преимущества перспективного деления, которое GPU уже выполняет:

Конечно, реальная сила этого подхода в том, что матрицу проекции можно перемножить с другими матрицами, позволяя объединять множество преобразований в одно.
Вторая причина заключается в том, что 1/z ― линейно в screen space (пространстве экрана), как подметил Emil Persson. Таким образом становится простой интерполяция d в треугольнике при растеризации, и такие вещи, как hierarchical Z-buffers, early Z-culling и сжатие depth buffer.
float dx = ddx(In.position.z);
float dy = ddy(In.position.z);
return 1000.0 * float4(abs(dx), abs(dy), 0, 0);
Здесь In.position ― это SV_Position. Результат выглядит как-то так:

Заметьте, все поверхности выглядят одноцветными. Разница в z от пикселя к пикселю одинакова для любого примитива. Это очень важно для GPU. Одна из причин ― интерполяция z дешевле, чем интерполяция w. Для z не нужно выполнять перспективную коррекцию. С более дешевыми аппаратными единицами можно обрабатывать большее количество пикселей за цикл с тем же бюджетом на транзисторы. Естественно, это очень важно для pre-z pass и shadow map. С современным аппаратным обеспечением линейность в screen space ― также очень полезное свойство для z-оптимизаций. Учитывая, что градиент линейный для всего примитива, также относительно легко вычислить точный диапазон глубины в пределах тайла для Hi-z culling. Это также означает, что возможен z-compression. С постоянной Δz в x и y вам не нужно хранить много информации, чтобы уметь полностью восстановить все значения z в тайле, при условии, что примитив покрыл весь тайл.
Графики карт глубины
Уравнения ― это сложно, давайте рассмотрим пару картинок!
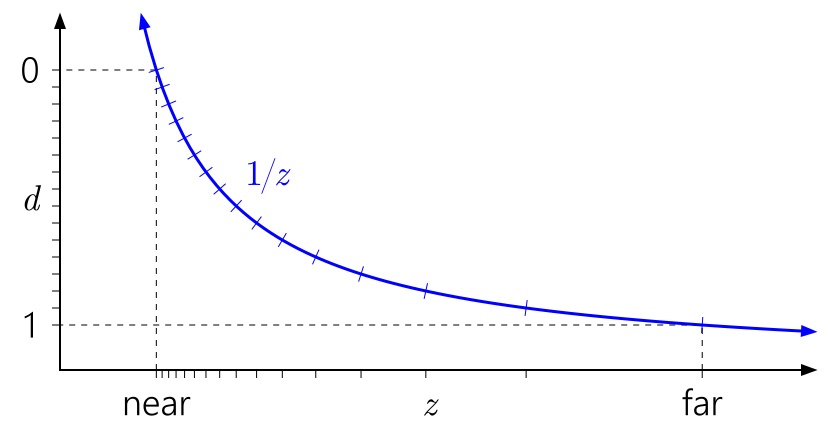
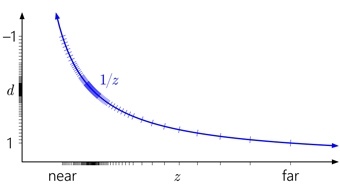
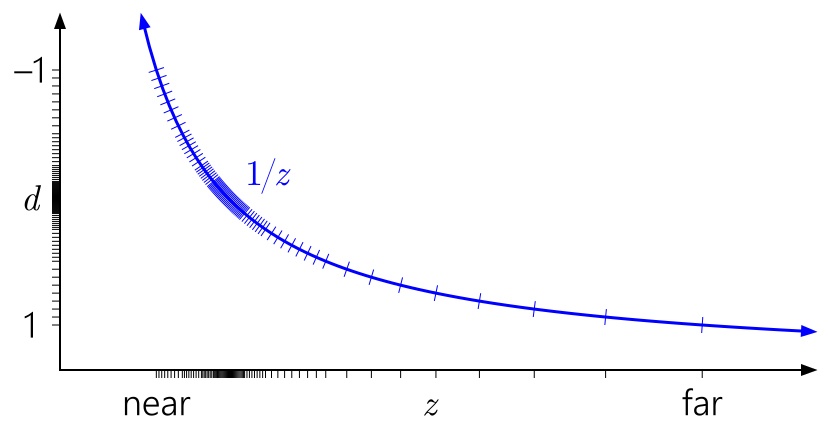
Способ чтения этих графиков: слева направо, затем вниз. Начните с d на левой оси. Так как d может быть произвольным линейным преобразованием от 1/z, мы можем расположить 0 и 1 в любое удобное место на оси. Отметки указывают на разные значения depth buffer. В целях наглядности я моделирую 4-битный целочисленный нормализованный depth buffer, так что есть 16 равномерно расположенных отметок.
На графике выше изображено “стандартное” ванильное преобразование глубины в D3D и аналогичных API. Вы сразу можете заметить как из-за кривой 1/z значения, близкие к near плоскости, сгруппированы, а значения, расположенные близко к far плоскости, разбросаны.
Также легко понять, почему near плоскость так сильно влияет на точность глубины. Отдаление near плоскости приведет к стремительному росту значений d относительно значений z, что приведет к еще более неравномерному распределению значений:
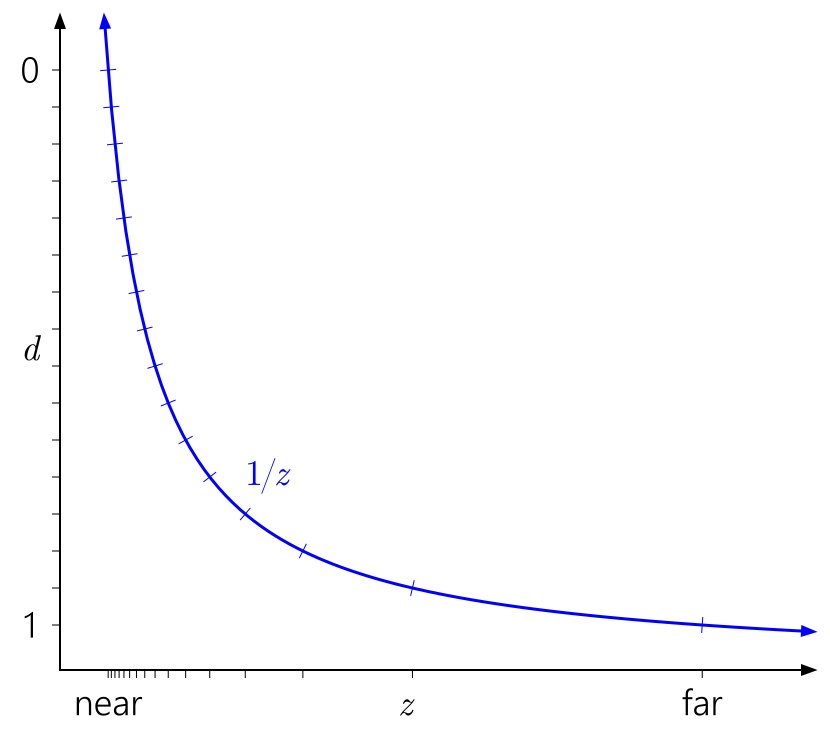
Аналогично в этом контексте легко заметить, почему отдаление far плоскости до бесконечности не имеет такого большого эффекта. Это просто означает расширение диапазона d до 1/z = 0:
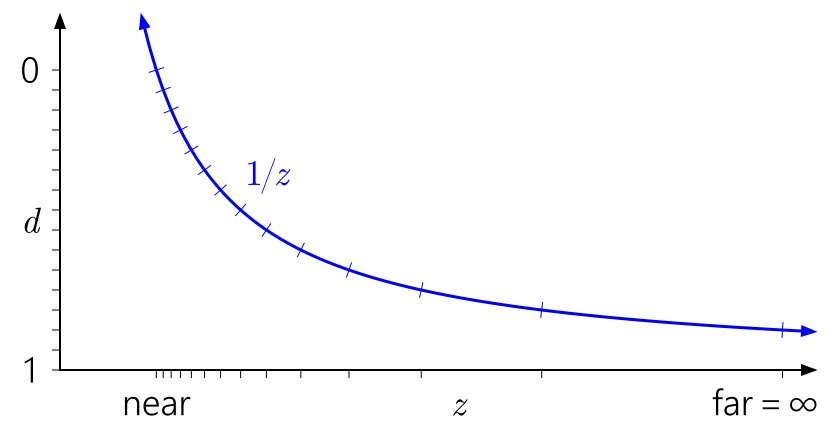
Но что насчет floating-point глубины? На следующем графике добавлены отметки, соответствующие float формату с 3 битами экспоненты и 3 битами мантиссы:

Теперь в диапазоне [0,1] есть 40 различных значений ― немного больше, чем 16 значений ранее, но большинство из них бесполезно сгруппированы близко к near плоскости (ближе к 0 у float точность выше), где большая точность нам действительно не нужна.
Сейчас широко известный трюк ― инвертировать depth, отображая near плоскость на d=1 и far плоскость на d=0:

Намного лучше! Теперь квази логарифмическое распределение float кое-как компенсирует нелинейность 1/z, при этом ближе к near плоскости дает точность, схожую с целочисленным depth buffer, и дает значительно большую точность где-либо еще. Точность глубины ухудшается очень медленно, если двигаться дальше от камеры.
Трюк reversed-Z, возможно, изобретался заново независимо несколько раз, но, по крайней мере, первое упоминание было в SIGGRAPH ’99 paper [Eugene Lapidous и Guofang Jiao (к сожалению нет в открытом доступе)]. И недавно он заново упоминался в блоге Мэттом Петинео и Брано Кеменом, и в выступлении Эмиля Перссона Creating Vast Game Worlds SIGGRAPH 2012.
Все предыдущие графики предполагали диапазон depth [0,1] после проецирования, что является соглашением в D3D. Что насчет OpenGL?
OpenGL по умолчанию предполагает диапазон depth [-1, 1] после проецирования. Для целочисленных форматов ничего не меняется, но для floating-point вся точность концентрируется бесполезно в середине. (Значение depth отображается в диапазон [0,1] для последующего хранения в depth buffer, но это не помогает, так как первоначальное отображение на [-1,1] уже уничтожило всю точность в дальней половине диапазона.) И из-за симметрии трюк reversed-Z здесь не сработает.
К счастью, в десктопном OpenGL это можно пофиксить с помощью широко поддерживаемого расширения ARB_clip_control (также начиная с OpenGL 4.5 в стандарт входит glClipControl). К сожалению, GL ES в пролете.
Влияние ошибки округления
Преобразование 1/z и выбор float vs int depth buffer ― это большая часть истории о точности, но не вся. Даже если вам хватает точности depth для представления сцены, которую вы пытайтесь отрендерить, легко ухудшить точность арифметическими ошибками в процессе преобразования вершин.
В начале статьи упоминалось, что Upchurch и Desbrun изучили данную проблему. Они предложили две основные рекомендации для минимизации ошибок округления:
- Использовать бесконечную far плоскость.
- Держать projection матрицу отдельно от других матриц, и применять ее отдельной операцией в вершинном шейдере, а не объединять ее с view матрицей.
Upchurch и Desbrun составили эти рекомендации с помощью аналитического метода, основанного на обработке ошибок округления как малых случайных погрешностей, представленных в каждой арифметической операции, и отслеживании их до первого порядка в процессе преобразования. Я решил проверить результаты на практике.
Исходники здесь ― Python 3.4 и numpy. Программа работает следующим образом: генерируется последовательность случайных точек, упорядоченная по глубине, расположенная линейно или логарифмически между near и far плоскостями. Затем точки умножаются на view и projection матрицы и выполняется перспективное деление, при этом используются 32-битные float-ы, и опционально конечный результат преобразуется в 24-битный int. В конце выполняется проход по последовательности и подсчет, сколько раз 2 соседние точки (которые изначально имели различную глубину) либо стали идентичными, так как у них совпал итоговый depth, либо вообще поменялся порядок. Другими словами программа измеряет частоту, с которой возникают ошибки сравнения depth ― что соответствует таким проблемам, как Z-fighting ― при различных сценариях.
Здесь представлены результаты для near = 0.1, far = 10K, с линейной глубиной 10K. (Я пробовал логарифмический интервал глубины и другие отношения near/far, и хотя конкретные числа менялись, общие тенденции в результатах были одинаковыми.)
В таблице, “eq” ― две точки с ближайшей глубиной получают одно и то же значение в depth buffer, и “swap” ― две точки с ближайшей глубиной поменялись местами.
| Составная view-projection матрица | Отдельные view и projection матрицы | |||
| float32 | int24 | float32 | int24 | |
| Не измененные значения Z (контрольный тест) | 0% eq 0% swap |
0% eq 0% swap |
0% eq 0% swap |
0% eq 0% swap |
| Стандартная проекция | 45% eq 18% swap |
45% eq 18% swap |
77% eq 0% swap |
77% eq 0% swap |
| Infinite far | 45% eq 18% swap |
45% eq 18% swap |
76% eq 0% swap |
76% eq 0% swap |
| Reversed Z | 0% eq 0% swap |
76% eq 0% swap |
0% eq 0% swap |
76% eq 0% swap |
| Infinite + reversed-Z | 0% eq 0% swap |
76% eq 0% swap |
0% eq 0% swap |
76% eq 0% swap |
| Стандартная + GL-style | 56% eq 12% swap |
56% eq 12% swap |
77% eq 0% swap |
77% eq 0% swap |
| Infinite + GL-style | 59% eq 10% swap |
59% eq 10% swap |
77% eq 0% swap |
77% eq 0% swap |
Извиняюсь за то, что без графика, здесь слишком большая размерность и просто так его не построить! В любом случае, глядя на числа, очевидны следующие выводы:
- В большинстве случаев нет разницы между int и float depth buffer. Арифметические ошибки расчета depth перекрывают ошибки преобразования в int. Частично потому, что у float32 и int24 почти равный ULP (единица наименьшей точности ― расстояние до ближайшего соседнего числа) на [0.5,1] (так как у float32 23-битная мантисса), так что почти на всем диапазоне глубины не добавляется ошибка преобразования в int.
- В большинстве случаев разделение view и projection матриц (следуя рекомендации Upchurch и Desbrun) улучшают результат. Несмотря на то, что общая частота ошибок не снижается, “свопы” становятся равными значениями, а это шаг в правильном направлении.
- Бесконечная far плоскость незначительно меняет частоту появления ошибок. Upchurch и Desbrun предсказали 25% снижение частоты численных ошибок (ошибки точности), но похоже это не приводит к снижению частоты ошибок сравнения.
Однако вышеупомянутые выводы не имеют реального значения по сравнению с магическим reversed-Z. Проверьте:
- Reversed-Z с float depth buffer дает в тесте нулевую частоту ошибок. Сейчас, конечно, вы можете получить некоторые ошибки, если продолжите увеличивать интервал входных значений depth. Тем не менее, reversed-Z с float смехотворно точнее, чем любой другой вариант.
- Reversed-Z с целочисленным depth buffer так же хорош, как и другие целочисленные варианты.
- Reversed-Z стирает различия между составной и раздельными view/projection матрицами, и конечной и бесконечной far плоскостями. Другими словами, с reversed-Z вы можете перемножить projection с другими матрицами, и использовать любую far плоскость, которую захотите, без ущерба для точности.
Заключение
Я думаю, что вывод здесь ясен. В любой ситуации, имея дело с перспективной проекцией, просто используйте float depth buffer и reversed-Z! И если у вас не получается использовать float depth buffer, вам все еще следует использовать reversed-Z. Это не панацея от всех бед, особенно если вы создаете open-world окружение с экстремальными диапазонами depth. Но это отличное начало.
Автор: migom





