Learn OpenGL. Урок 5.4 – Всенаправленные карты теней

Всенаправленные карты теней

В предыдущем уроке мы разобрались с созданием динамических проекционных теней. Эта техника отлично работает, но, увы, подходит она только для направленных источников света, поскольку карта теней создается в одном направлении, совпадающим с направлением источника. Именно поэтому данная техника также называется направленной картой теней, так как карта глубин (карта теней) создается именно вдоль направления действия источника света.
Данный же урок будет посвящён созданию динамических теней, проецирующихся во всех направлениях. Этот подход отлично подходит для работы с точечными источниками освещения, ведь они должны отбрасывать тени во всех направлениях сразу. Соответственно, данная техника называется всенаправленной картой теней.

Урок во многом опирается на материалы предыдущего урока, так что если вы еще не практиковались с обычными картами теней, стоит сделать это перед продолжением изучения этой статьи.

В целом, алгоритм работы остается практически идентичным таковому для направленных теней: создаем карту глубин с точки зрения источника света и для каждого фрагмента сравниваем значения его глубины и считанного из карты глубин. Главное отличие направленного и всенаправленного подхода в типе применяющейся карты глубин.
Карта теней, которая нам потребуется, подразумевает рендер сцены во всех направлениях вокруг источника света и обычная 2D текстура здесь не годится. Так, может, использовать кубическую карту? Поскольку кубическая карта может хранить данные об окружении с помощью всего шести граней, то можно отрисовать всю сцену на каждую из этих граней и затем осуществлять выборку глубины из кубической карты.

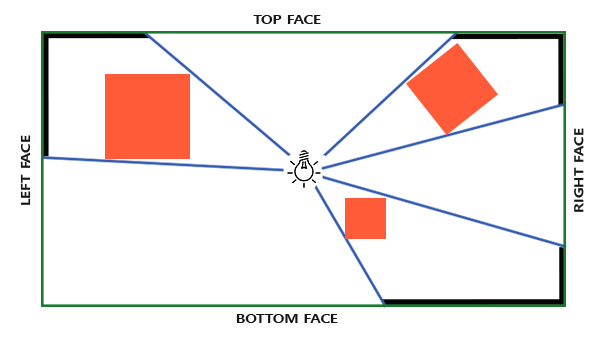
Созданная кубическая карта теней в итоге попадает во фрагментный шейдер, где осуществляется выборка из нее с помощью вектора направления для получения значения глубины фрагмента (с точки зрения источника). Большую часть технически сложных деталей мы уже обсудили в предыдущем уроке, так что остается одна тонкость – использование кубической карты.

Создание кубической карты

Для создания кубической карты, хранящей значения глубины окружения источника света, нам потребуется отрендерить сцену шесть раз: по разу для каждой грани карты. Одним из (очевидных) способов это осуществить будет просто отрисовать сцену шесть раз, используя шесть разных видовых матриц, и в каждый проход подключая отдельную грань кубической карты к прикреплению цвета объекта кадрового буфера:

for(unsigned int i = 0; i < 6; i++)
{
    GLenum face = GL_TEXTURE_CUBE_MAP_POSITIVE_X + i;
    glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, face, depthCubemap, 0);
    BindViewMatrix(lightViewMatrices[i]);
    RenderScene();  
}

Такой подход может оказаться весьма затратным по производительности, поскольку множество вызовов отрисовки осуществляется для создания единственной карты теней. В уроке мы попробуем реализовать более оптимальный подход, используя небольшую хитрость, связанную с использованием геометрического шейдера. Это позволит создать кубическую карту глубин всего за один проход.
Сначала создадим кубическую карту:

unsigned int depthCubemap;
glGenTextures(1, &depthCubemap);

И каждую грань зададим как 2D текстуру, хранящую значения глубины:

const unsigned int SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
for (unsigned int i = 0; i < 6; ++i)
        glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_DEPTH_COMPONENT, 
                     SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL); 

Также не забудем задать подходящие параметры текстуры:

glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);  

В обычном подходе мы бы подключали каждую грань кубической карты к кадровому буферу и рендерили бы сцену шесть раз, в каждом проходе заменяя грань кубической карты, подключенную к прикреплению глубины буфера кадра. Но с использованием геометрического шейдера мы сможем вывести сцену сразу на все грани в один проход, а потому подключаем кубическую карту напрямую к прикреплению глубины:

glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glFramebufferTexture(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, depthCubemap, 0);
glDrawBuffer(GL_NONE);
glReadBuffer(GL_NONE);
glBindFramebuffer(GL_FRAMEBUFFER, 0);  

И снова отмечу вызовы glDrawBuffer и glReadBuffer: поскольку нам важны только значения глубины, мы явно указываем OpenGL, что можно не осуществлять запись в буфер цвета.
В конечном итоге здесь будет применяться два прохода: первым подготавливается карта теней, вторым рисуется сцена, а карта используется для создания затенения. С использованием кадрового буфера и кубической карты код выглядит примерно так:

// 1. рендер в кубическую карту глубин
glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
    glClear(GL_DEPTH_BUFFER_BIT);
    ConfigureShaderAndMatrices();
    RenderScene();
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 2. обычный рендер сцены с использованием кубической карты глубин для затенения
glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
ConfigureShaderAndMatrices();
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
RenderScene();

В первом приближении процесс идет так же, как и при использовании направленных карт теней. Отличие только в том, что мы осуществляем рендер в кубическую карту глубины, а не в привычную 2D текстуру.
Прежде чем мы приступим к непосредственному рендеру сцены со направлений, относительно источника, нам необходимо подготовить подходящие матрицы трансформации.

Преобразование в систему координат источника света

Имея подготовленный объект буфера кадра и кубическую карту мы переходим к вопросу трансформации всех объектов сцены в координатные пространства, соответствующие всем шести направлениям от источника света. Составим матрицы преобразования так же, как и в предыдущем уроке, но в этот раз нам понадобится отдельная матрица для каждой грани.
Каждое итоговое преобразование в пространство источника содержит как матрицу проекции, так и видовую матрицу. Для матрицы проекции используем матрицу перспективной проекции: источник представляет собой точку в пространстве, поэтому перспективная проекция здесь подходит больше всего. Данная матрица будет одинакова для всех итоговых преобразований:

float aspect = (float)SHADOW_WIDTH/(float)SHADOW_HEIGHT;
float near = 1.0f;
float far = 25.0f;
glm::mat4 shadowProj = glm::perspective(glm::radians(90.0f), aspect, near, far); 

Отмечу важный момент: параметр угла обзора при формировании матрицы устанавливается в 90°. Именно это значение угла обзора обеспечивает нам проекцию, позволяющую корректно заполнить грани кубической карты, чтобы они сходились без разрывов.
Поскольку матрица проекции остается постоянной, то можно повторно использовать одну и ту же матрицу для создания всех шести матриц итогового преобразования. Но видовые матрицы нужны уникальные для каждой грани. Используя glm::lookAt создадим шесть матриц, представляющих шесть направлений в следующем порядке: право, лево, верх, низ, ближняя грань, дальняя грань:

std::vector<glm::mat4> shadowTransforms;
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3( 1.0, 0.0, 0.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3(-1.0, 0.0, 0.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 1.0, 0.0), glm::vec3(0.0, 0.0, 1.0));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3( 0.0,-1.0, 0.0), glm::vec3(0.0, 0.0,-1.0));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 0.0, 1.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 0.0,-1.0), glm::vec3(0.0,-1.0, 0.0));

В приведенном коде шесть созданных видовых матриц умножаются на матрицу проекции для задания шести уникальных матриц преобразование в пространство источника света. Параметр target в вызове glm::lookAt представляет собой направление взгляда на каждую из граней кубической карты.
Далее этот список матриц передается в шейдеры при рендере кубической карты глубин.

Шейдеры записи глубины

Для записи глубины в кубическую карту мы используем три шейдера: вершинный, фрагментный и дополнительный геометрический, который исполняется между этими стадиями.
Именно геометрический шейдер будет отвечать за преобразование всех вершин в мировом пространстве в шесть отдельных пространств источника света. Таким образом, вершинный шейдер тривиален и просто выдает координаты вершины в мировом пространстве, которые уйдут в геометрический шейдер:

#version 330 core
layout (location = 0) in vec3 aPos;

uniform mat4 model;

void main()
{
    gl_Position = model * vec4(aPos, 1.0);
}  

Геометрический шейдер принимает на входе три вершины треугольника, а также юниформ с массивом матриц преобразования в пространства источника света. Здесь и кроется интересный момент: именно геометрический шейдер будет заниматься преобразованием вершин из мировых координат в пространства источника.
Для геометрического шейдера доступна встроенная переменная gl_Layer, которая задает номер грани кубической карты для который шейдер будет формировать примитив. В обычной ситуации шейдер просто отправляет все примитивы дальше в пайплайн без дополнительных действий. Но изменением значения этой переменной мы можем управлять тем, в какую грань кубической карты мы собираемся рендерить каждый из обрабатываемых примитивов. Конечно, это работает только в том случае, если к кадровому буферу подключена кубическая карта.

#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices=18) out;

uniform mat4 shadowMatrices[6];
// переменная FragPos вычисляется в геометрическом шейдере 
// и выдается для каждого вызова EmitVertex()
out vec4 FragPos; 

void main()
{
    for(int face = 0; face < 6; ++face)
    {
        // встроенная переменная, определяющая в какую 
        // грань кубической карты идет рендер
        gl_Layer = face; 
        for(int i = 0; i < 3; ++i) // цикл по всем вершинам треугольника
        {
            FragPos = gl_in[i].gl_Position;
            gl_Position = shadowMatrices[face] * FragPos;
            EmitVertex();
        }    
        EndPrimitive();
    }
}  

Представленный код должен быть довольно понятен. Шейдер получает примитив типа треугольника на входе, а в качестве результата выдает шесть треугольников (6 * 3 = 18 вершин). В функции main мы проходим в цикле по всем шести граням кубической карты, устанавливая текущий индекс как номер активной грани кубической карты соответствующей записью в переменную gl_Layer. Также мы преобразуем каждый входные вершины из мировой системы координат в соответствующее текущей грани кубической арты пространство источника света. Для этого FragPos умножается на подходящую матрицу преобразования из массива-юниформа shadowMatrices. Обратите внимание, что значение FragPos также передается во фрагментный шейдер для вычисления глубины фрагмента.
В прошлом уроке мы использовали пустой фрагментный шейдер, а вычислением глубины для карты теней была занята сама OpenGL. В этот раз мы вручную сформируем линейное значение глубины, взяв за основу расстояние между положением фрагмента и источником света. Такой расчет значения глубины делает последующие расчеты затенения немного более интуитивными.

#version 330 core
in vec4 FragPos;

uniform vec3 lightPos;
uniform float far_plane;

void main()
{
    // вычисление расстояния между фрагментом и источником 
    float lightDistance = length(FragPos.xyz - lightPos);
    
    // преобразование к интервалу [0, 1] посредством деления на far_plane
    lightDistance = lightDistance / far_plane;
    
    // запись результата в результирующую глубину фрагмента
    gl_FragDepth = lightDistance;
}  

На вход фрагментного шейдера попадает переменная FragPos из геометрического шейдера, вектор положения источника, а также расстояние до дальней плоскости отсечения пирамиды проекции источника света. В данном коде мы просто вычисляем расстояние между фрагментом и источником, приводим к диапазону значений [0., 1.] и записываем как результат выполнения шейдера.
Рендер сцены с этими шейдерами и подключенной к объекту кадрового буфера кубической картой должно сгенерировать полностью подготовленную карту теней для использования в следующем проходе рендера.

Всенаправленные карты теней

Раз у нас все подготовлено, то можно приступать к непосредственному рендеру всенаправленных теней. Порядок действий схож с тем, что был представлен в предыдущем уроке для направленных теней, но в этот раз мы используем в качестве карты глубин кубическую текстуру вместо двухмерной, а также передаем в шейдеры юниформ со значением дальней плоскости пирамиды проекции для источника света.

glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
shader.use();  
// ... передача данных юниформов в шейдер (включая параметр матрицы проекции источника света far_plane)
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
// ... привязка текстур
RenderScene();

В примере функция renderScene выводит несколько кубиков, расположенных в большом кубическом помещении, которые будут отбрасывать тени от источника света, расположенного в центре сцены.
Вершинный и фрагментный шейдеры практически идентичны рассмотренных в уроке по направленным теням. Так, во фрагментном шейдере теперь не требуется входной параметр положения фрагмента в пространстве источника света, так как выборка из карты теней теперь делается с помощью вектора направления.
Вершинный шейдер, соответственно, теперь не должен преобразовывать вектор положения в пространство источника света, так что мы можем выкинуть переменную FragPosLightSpace:

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;

out vec2 TexCoords;

out VS_OUT {
    vec3 FragPos;
    vec3 Normal;
    vec2 TexCoords;
} vs_out;

uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;

void main()
{
    vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
    vs_out.Normal = transpose(inverse(mat3(model))) * aNormal;
    vs_out.TexCoords = aTexCoords;
    gl_Position = projection * view * model * vec4(aPos, 1.0);
}  

Код модели освещения Блинна-Фонга во фрагментном шейдере остается нетронутым, в нем также оставлено умножение на коэффициент затенения в конце:

#version 330 core
out vec4 FragColor;

in VS_OUT {
    vec3 FragPos;
    vec3 Normal;
    vec2 TexCoords;
} fs_in;

uniform sampler2D diffuseTexture;
uniform samplerCube depthMap;

uniform vec3 lightPos;
uniform vec3 viewPos;

uniform float far_plane;

float ShadowCalculation(vec3 fragPos)
{
    [...]
}

void main()
{           
    vec3 color = texture(diffuseTexture, fs_in.TexCoords).rgb;
    vec3 normal = normalize(fs_in.Normal);
    vec3 lightColor = vec3(0.3);
    // ambient
    vec3 ambient = 0.3 * color;
    // diffuse
    vec3 lightDir = normalize(lightPos - fs_in.FragPos);
    float diff = max(dot(lightDir, normal), 0.0);
    vec3 diffuse = diff * lightColor;
    // specular
    vec3 viewDir = normalize(viewPos - fs_in.FragPos);
    vec3 reflectDir = reflect(-lightDir, normal);
    float spec = 0.0;
    vec3 halfwayDir = normalize(lightDir + viewDir);  
    spec = pow(max(dot(normal, halfwayDir), 0.0), 64.0);
    vec3 specular = spec * lightColor;    
    // calculate shadow
    float shadow = ShadowCalculation(fs_in.FragPos);                      
    vec3 lighting = (ambient + (1.0 - shadow) * (diffuse + specular)) * color;    
    
    FragColor = vec4(lighting, 1.0);
}  

Также отмечу несколько тонких отличий: код модели освещения действительно неизменен, но теперь используется сэмплер типа samplerCubemap, а функция ShadowCalculation принимает координаты фрагмента в мировых координатах, вместо пространства источника света. Также мы используем параметр пирамиды проекции источника света far_plane в дальнейших расчетах. В конце шейдера мы вычисляем коэффициент затенения, который равен 1 при нахождении фрагмента в тени; или 0 при нахождении фрагмента вне тени. Данный коэффициент используется для воздействия на подготовленные значения диффузной и зеркальной составляющих освещения.
Самые большие изменения касаются тела функции ShadowCalculation, где выборка значения глубины теперь ведется из кубической карты, а не 2D текстуры. Разберем код этой функции по порядку.
Первым делом необходимо получить непосредственное значение глубины из кубической карты. Как вы помните, при подготовке кубической карты мы записали в нее глубину, представленную в виде дистанции между фрагментом и источником света. Тот же подход используется здесь:

float ShadowCalculation(vec3 fragPos)
{
    vec3 fragToLight = fragPos - lightPos; 
    float closestDepth = texture(depthMap, fragToLight).r;
}  

Вычисляется вектор разницы между положением фрагмента и источника света, который используется в качестве вектора направления для выборки из кубической карты. Как мы помним, вектор выборки из кубической карты не обязательно должен иметь единичную длину, потом не необходимости его нормализовывать. Полученное значение closestDepth – нормализованное значение глубины ближайшего видимого фрагмента относительно источника света.
Поскольку значение closestDepth заключено в интервале [0., 1.], то сперва следует провести обратное преобразование в интервал [0., far_plane]:

closestDepth *= far_plane;  

Далее, мы получаем значение глубины для текущего фрагмента относительно источника света. Для выбранного подхода это предельно просто: нужно только вычислить длину уже подготовленного вектора fragToLight:

float currentDepth = length(fragToLight);  

Таким образом получим значение глубины, лежащее в том же (а, может, и в большем) интервале, что и closestDepth.
Теперь мы можем приступить к сравнению обоих значений глубины, дабы выяснить, находится ли текущий фрагмент в тени или нет. Также мы сразу включаем в сравнение значение смещения, чтобы не столкнуться с проблемой «теневой ряби», объясненной в предыдущем уроке:

float bias = 0.05; 
float shadow = currentDepth -  bias > closestDepth ? 1.0 : 0.0; 

Полный код ShadowCalculation:

float ShadowCalculation(vec3 fragPos)
{
    // get vector between fragment position and light position
    vec3 fragToLight = fragPos - lightPos;
    // use the light to fragment vector to sample from the depth map    
    float closestDepth = texture(depthMap, fragToLight).r;
    // it is currently in linear range between [0,1]. Re-transform back to original value
    closestDepth *= far_plane;
    // now get current linear depth as the length between the fragment and light position
    float currentDepth = length(fragToLight);
    // now test for shadows
    float bias = 0.05; 
    float shadow = currentDepth -  bias > closestDepth ? 1.0 : 0.0;

    return shadow;
}  

С приведенными шейдерами приложение уже выводит вполне сносные тени и в этом раз они отбрасываются во все стороны от источника. Для сцены с источником в центре, картинка представляется следующая:

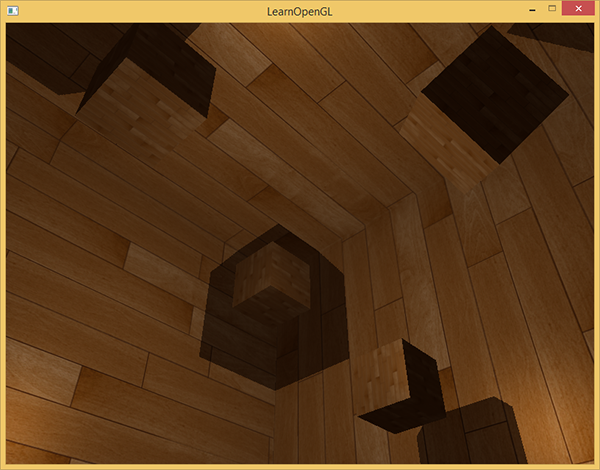
Полный исходный код лежит здесь.

Визуализация кубической карты глубин

Если вы в чем-то похожи на меня, то, думается, с первого раза у вас не получится сделать все верно, и потому какое-то средство отладки приложения вполне бы пригодилось. Как самый очевидный вариант было бы неплохо иметь возможность проверить корректность подготовки карты глубин. Поскольку у нас теперь используется кубическая карта, а не двухмерная текстура, вопрос визуализации требует несколько более замысловатого подхода.
Простым выходом было бы взять нормализованное значение closestDepth из тела функции ShadowCalculation и вывести его как результат фрагментного шейдера:

FragColor = vec4(vec3(closestDepth / far_plane), 1.0);  

В результате получается сцена в градациях серого, где интенсивность цвета соответствует линейному значению глубины в данной сцене:

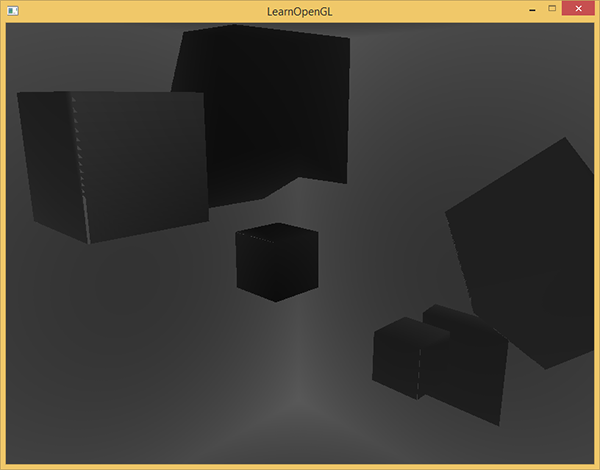
Также видны области затенения на стенах помещения. Если результат визуализации схож с приведенным, то можно быть уверенным, что карты теней подготовлена верно. В противном случае где-то закралась ошибка: например, значение closestDepth было взято из интервала [0., far_plane].

Percentage-closer filtering

Поскольку всенаправленные тени строятся на тех же принципах, что и направленные тени, они унаследовали все артефакты, связанные с точностью и конечностью разрешения текстур. Если приблизиться к границам затененных областей, то становятся видны зазубренные края, т.е. артефакты алиасинга. Фильтрация по методу Percentage-closer filtering (PCF) позволяет сгладить следы алиасинга с помощью фильтрации множества выборок глубины вокруг текущего фрагмента и усреднения результата сравнения глубин.
Возьмем код PCF из предыдущего урока и добавим третье измерение (выборка из кубической карты ведь требует вектора направления):

float shadow  = 0.0;
float bias    = 0.05; 
float samples = 4.0;
float offset  = 0.1;
for(float x = -offset; x < offset; x += offset / (samples * 0.5))
{
    for(float y = -offset; y < offset; y += offset / (samples * 0.5))
    {
        for(float z = -offset; z < offset; z += offset / (samples * 0.5))
        {
            float closestDepth = texture(depthMap, fragToLight + vec3(x, y, z)).r; 
            closestDepth *= far_plane;   // Undo mapping [0;1]
            if(currentDepth - bias > closestDepth)
                shadow += 1.0;
        }
    }
}
shadow /= (samples * samples * samples);

Отличий немного. Рассчитываем смещения для текстурных координат динамически, на основе количества выборок, которые хотим сделать по каждой оси и усредняем результат делением на число выборок, возведенное в куб.
Теперь тени выглядят намного более достоверно и края их достаточно гладкие.

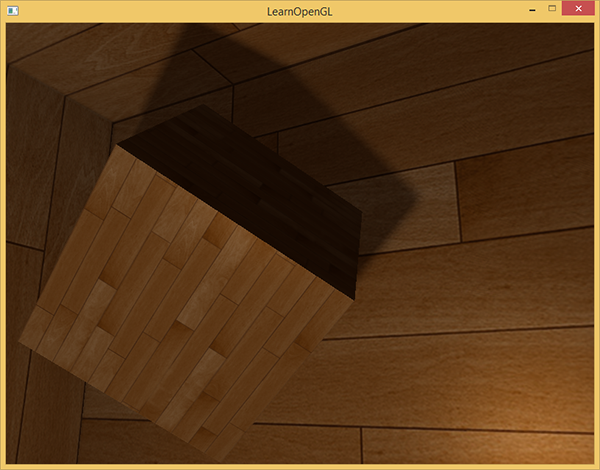
Однако, установив число выборок samples = 4, мы по факту потратим целых 64 выборки на каждый фрагмент, что очень много.
И в большинстве случаев эти выборки будут излишними, поскольку окажутся очень близкими к исходному вектору выборки. Пожалуй, было бы более полезно делать выборки в направлениях, перпендикулярных исходному вектору выборки. Увы, простого метода для выяснения, какие из порожденных дополнительных направлений окажутся излишними не существует. Можно воспользоваться одним приемом и задаться массивом направлений смещения, которые все являются практически полностью разделимыми векторами, т.е. каждый из них будет указывать в совершенно разные стороны. Это уменьшит количество направлений смещения, которые окажутся слишком близки друг к другу. Ниже как раз приведен подобный массив с двадцатью специально подобранными направлениями смещения:

vec3 sampleOffsetDirections[20] = vec3[]
(
   vec3( 1,  1,  1), vec3( 1, -1,  1), vec3(-1, -1,  1), vec3(-1,  1,  1), 
   vec3( 1,  1, -1), vec3( 1, -1, -1), vec3(-1, -1, -1), vec3(-1,  1, -1),
   vec3( 1,  1,  0), vec3( 1, -1,  0), vec3(-1, -1,  0), vec3(-1,  1,  0),
   vec3( 1,  0,  1), vec3(-1,  0,  1), vec3( 1,  0, -1), vec3(-1,  0, -1),
   vec3( 0,  1,  1), vec3( 0, -1,  1), vec3( 0, -1, -1), vec3( 0,  1, -1)
);   

Далее, мы можем модифицировать алгоритм PCF для использования массивов с фиксированным размером подобных sampleOffsetDirections в процессе выборки из кубической карты. Главное преимущество подобного подхода заключается в создании результата, визуально схожего с первым подходом, но требующего значительно меньшее количество дополнительных выборок.

float shadow = 0.0;
float bias   = 0.15;
int samples  = 20;
float viewDistance = length(viewPos - fragPos);
float diskRadius = 0.05;
for(int i = 0; i < samples; ++i)
{
    float closestDepth = texture(depthMap, fragToLight + sampleOffsetDirections[i] * diskRadius).r;
    closestDepth *= far_plane;   // Undo mapping [0;1]
    if(currentDepth - bias > closestDepth)
        shadow += 1.0;
}
shadow /= float(samples);  

В приведенном коде вектор смещения умножается на величину diskRadius, представляющую радиус диска, построенного вокруг исходного вектора выборки fragToLight и в пределах которого производится дополнительные выборки.
Можно пойти еще дальше и провернуть следующий трюк: попробуем менять величину diskRadius в соответствии с удалением наблюдателя от фрагмента. Так мы сможем увеличить радиус смещения и сделать тени мягче для удаленных фрагментов, резче для близких к наблюдателю фрагментов:

float diskRadius = (1.0 + (viewDistance / far_plane)) / 25.0;  

Результат такого алгоритма PCF выдает мягкие тени не хуже, если не лучше, чем исходный подход:

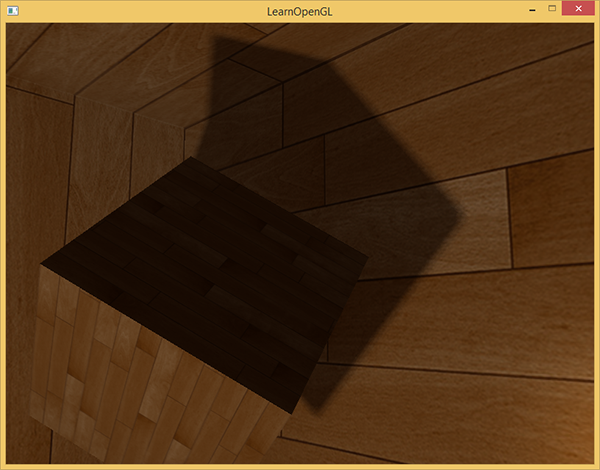
Безусловно, величина bias, которая добавляется для каждого фрагмента чрезвычайно сильно зависит от контекста и содержания сцены, а потому всегда будет требовать дополнительной экспериментальной настройки. Поэкспериментируйте с параметрами предложенного алгоритма, чтобы увидеть их влияние на итоговую картинку.
Исходный код примера можно найти здесь.

Также отмечу, что использование геометрического шейдера для создания кубической карты глубин не обязательно окажется быстрее, чем шестикратный рендер сцены для каждой её грани. Применение такого подхода накладывает свои собственные негативные эффекты, касающиеся производительности. Вполне возможно, что негативный вклад в производительность вообще перевесит весь выигрыш от использования геометрического шейдера и единственного вызова отрисовки. И, конечно, это зависит от того, в каком окружении вы работаете, какая видеокарта и какие драйверы вам доступны, и еще от множества других вещей. Поэтому, если производительность для вас действительно важна, то всегда стоит проводить профилирование всех рассматривающихся альтернатив и выбирать оказавшийся наиболее эффективным для сцены в приложении. Лично я придерживаюсь использования геометрических шейдеров для задачи создания карт теней, поскольку вижу их более интуитивными в использовании.

Дополнительные материалы:

• Shadow Mapping for point light sources in OpenGL: урок по всенаправленным картам теней от sunandblackcat.
• Multipass Shadow Mapping With Point Lights: аналогично, но от автора ogldev.
• Omni-directional Shadows: занимательная презентация, касательно всенаправленных карт теней, от Peter Houska.

P.S.: У нас есть телеграм-конфа для координации переводов. Если есть серьезное желание помогать с переводом, то милости просим!

Автор: UberSchlag

Источник