Процедурная растительность на OpenGL и GLSL

В этом посте я хотел бы рассказать об использовании аппаратной тесселяции и геометрического шейдера для генерации большого количества геометрии на основе минимальных входных данных. Надеюсь, пост будет полезен тем, кто имеет начальное представление о программировании шейдеров, но ещё не познал всю мощь программируемого графического конвейера. Это не руководство по шейдерам для начинающих, поэтому многие моменты их работы заметены под ковёр или снабжены ссылкой на соответствующую документацию.

Повествование будет вестись на примере небольшой демки, которая генерирует сцену как на картинке выше. Мы пройдём увлекательное путешествие от подготовки данных на CPU до записи значений цвета на выход фрагментного шейдера.

Цели и средства

При написании демки я поставил перед собой следующие цели:

• Максимально сократить объём данных, хранимых в видеопамяти. Как следствие:
• Максимально утилизировать графический процессор, используя все доступные стадии конвейера.
• Сделать некоторые параметры сцены настраиваемыми.
• Сосредоточиться на геометрии и написании шейдеров, потратив минимум усилий на остальные компоненты. Поэтому был использован наиболее привычный мне инструментарий: C++11 (gcc), Qt5 + qmake, GLSL.
• По возможности упростить сборку и запуск получившейся демки на различных платформах.

Исходя из этого списка, пришлось пожертвовать проработкой некоторых моментов:

• Основной цикл сделан примитивно. Поэтому скорость анимации и перемещения камеры зависит от частоты кадров, а значит и от положения камеры в пространстве.
• В единый класс камеры замешаны её координаты, ориентация, проекция и функции для изменения всего этого. В таком виде его написание не заняло много времени и позволило сделать достаточно оптимальный проброс параметров камеры в шейдер.
• Класс шейдера выполнен в виде достаточно тонкой обёртки над соответствующим классом Qt5. Общие для различных стадий куски кода склеиваются воедино и отдаются на откуп оптимизатору компилятора, который выкинет неиспользуемый код и глобальные переменные.
• В программе используется единственный шейдер, поэтому передача данных в него сделана без «новомодных» UBO. В этом случае они не добавили бы производительности, усложнив код.
• Счётчик кадров в секунду сделан на основе запросов OpenGL. Поэтому он показывает не «настоящие» FPS, а немного завышенный идеализированный показатель, в котором не учитывается оверхед, привносимый Qt.
• Крутое освещение не было целью написания данной демки, поэтому используется простая реализация освещения Фонга с одним, захардкоженным в шейдере, источником света.
• Реализация шумов в шейдерах была взята у стороннего автора.

Дабы предоставить возможность читателю обозревать весь код демки по ходу повествования, сразу приведу ссылку на репозиторий.

Краткий обзор генерации геометрии

Мы будем отрисовывать набор патчей, каждый из которых содержит единственную вершину. Каждая вершина, в свою очередь, содержит единственный четырёхкомпонентный атрибут. Используя эту минимальную порцию данных в качестве затравки, мы «нарастим» на каждый такой патч (т.е. на одну точку) целый куст шевелящихся стеблей. Кроме того, все кусты могут быть подвержены действию ветра с задаваемыми пользователем параметрами. Большая часть работы по генерации куста выполняется в шейдере тесселяции (Tesselation evaluation shader) и в геометрическом шейдере. Так, в шейдере тесселяции генерируется скелет куста со всеми деформациями, вносимыми шевелением и ветром, а в геометрическом шейдере на этот скелет натягивается полигональная «плоть», толщина которой зависит от высоты кости на скелете. Фрагментный шейдер, как водится, вычисляет освещение и наносит процедурно генерируемую текстуру на основе диаграммы Вороного.

Итак, начнём!

CPU

Путь данных к раскрашиванию пикселей монитора начинается с их подготовки на CPU. Как было сказано выше, каждая «модель» сцены изначально состоит из одной вершины. Сделаем эту вершину четырёхмерной, где первые три компоненты — это положение вершины в пространстве, а четвёртая компонента — количество стеблей в кусте. Таким образом, кусты смогут отличаться друг от друга количеством стеблей. Начнём генерацию координат с узлов квадратной решётки конечного размера, и возмутим каждую координату на случайную величину из заданного интервала:

const int numNodes = 14; // Количество узлов решётки вдоль одной стороны.
const GLfloat gridStep = 3.0f; // Шаг решётки.
// Максимальные смещения в горизонтальной плоскости:
const GLfloat xDispAmp = 5.0f; 
const GLfloat zDispAmp = 5.0f;
const GLfloat yDispAmp = 0.3f; // Максимальное смещение по вертикали.
numClusters = numNodes * numNodes; // Количество кустов.
GLfloat *vertices = new GLfloat[numClusters * 4]; // Буфер для генерируемых вершин.
std::random_device rd;
std::mt19937 mt(rd());
std::uniform_real_distribution<GLfloat> xDisp(-xDispAmp, xDispAmp);
std::uniform_real_distribution<GLfloat> yDisp(-yDispAmp, yDispAmp);
std::uniform_real_distribution<GLfloat> zDisp(-zDispAmp, zDispAmp);
std::uniform_int_distribution<GLint> numStems(12, 64); // Количество стеблей.
for(int i = 0; i < numNodes; ++i) {
    for(int j = 0; j < numNodes; ++j) {
	const int idx = (i * numNodes + j) * 4;
	vertices[idx]     = (i - numNodes / 2) * gridStep + xDisp(mt);
	vertices[idx + 1] = yDisp(mt);
	vertices[idx + 2] = (j - numNodes / 2) * gridStep + zDisp(mt);
	vertices[idx + 3] = numStems(mt);
    }
}

Сгенерированные данные отправим в видеопамять:

GLuint vao; // https://www.opengl.org/wiki/Vertex_Specification#Vertex_Array_Object
GLuint posVbo; // https://www.opengl.org/wiki/Vertex_Specification#Vertex_Buffer_Object
glGenVertexArrays(1, &vao);
glBindVertexArray(vao);
glGenBuffers(1, &posVbo);
glEnableVertexAttribArray(ATTRIBINDEX_VERTEX);
glBindBuffer(GL_ARRAY_BUFFER, posVbo);
glVertexAttribPointer(ATTRIBINDEX_VERTEX, 4, GL_FLOAT, GL_FALSE, 0, 0);
glBufferData(GL_ARRAY_BUFFER, sizeof(GLfloat) * numClusters * 4, vertices, GL_STATIC_DRAW);
glFinish();
delete[] vertices;

Теперь метод отрисовки всего газона из сгенерированной травы выглядит очень лаконично:

void ProceduralGrass::draw() {
    glBindVertexArray(vao);
    glPatchParameteri(GL_PATCH_VERTICES, 1);
    glDrawArrays(GL_PATCHES, 0, numClusters);
    glBindVertexArray(0);
}

Кроме геометрии, в шейдерах нам понадобятся равномерно распределённые случайные числа. Наиболее оптимально на CPU получить числа в интервале [0; 1], а на GPU в каждом конкретном месте приводить их к требуемому интервалу. В видеопамять мы их доставим в виде одномерной текстуры, у которой в качестве фильтрации установлен выбор ближайшего значения. Напомню, что в двумерном случае такая фильтрация приводит к подобному результату:

Источник

Код генерации и настройки текстуры:

const GLuint randTexSize = 256;
GLfloat randTexData[randTexSize];
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_real_distribution<float> dis(0.0f, 1.0f);
std::generate(randTexData, randTexData + randTexSize, [&](){return dis(gen);});
// Create and tune random texture.
glGenTextures(1, &randTexture);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_1D, randTexture);
glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_BASE_LEVEL, 0);
glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_MAX_LEVEL, 0);
glTexImage1D(GL_TEXTURE_1D, 0, GL_R16F, randTexSize, 0, GL_RED, GL_FLOAT, randTexData);
glUniform1i(glGetUniformLocation(grassShader.programId(), "urandom01"), 0);

Вершинный шейдер

Как правило, при использовании тесселяции вершинный шейдер получается очень ленивым, так как с него начинается конвейер, а геометрии как таковой ещё нет. В нашем случае вершинный шейдер тривиален. В нём мы просто отправим точку со входа сразу на выход:

layout(location=0) in vec4 position;
void main(void) {
    gl_Position = position;
}

Тесселяция

Аппаратная тесселяция — это мощная техника повышения детализации полигональных моделей средствами GPU. Не путайте с алгоритмами разбиения полигонов на треугольники, выполняемыми на центральном процессоре. Аппаратная тесселяция состоит из трёх стадий графического конвейера, две из которых можно программировать (выделены жёлтым):

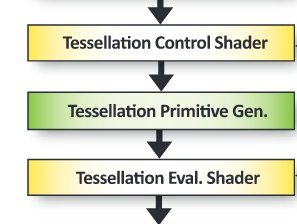
Подробнее о шейдерах и их входах/выходах рассказано ниже. Здесь стоит сказать, что на вход тесселяции подаётся патч, состоящий из произвольного количества вершин, которое фиксировано для каждого вызова glDraw* и ограничено как минимум числом 32. Атрибуты этих вершин не имеют каких либо выделенных значений, а значит в обоих шейдерах программист волен интерпретировать их как угодно. Это даёт поистине фантастические возможности по сравнению со старыми вершинными шейдерами.

Модель работы программируемой тесселяции существенно отличается от других шейдеров, и может вызвать недоумение при первом знакомстве с ней, даже если у вас есть опыт работы с вершинными и геометрическими шейдерами.

Шейдер управления тесселяцией

В общем случае шейдеру управления тесселяцией доступны все вершины входного патча, прошедшие через вершинный шейдер по отдельности. На его вход поступает поступает количество вершин в патче gl_PatchVerticesIn, порядковый номер патча gl_PrimitiveID и порядковый номер выходной вершины gl_InvocationID, о котором позже. Порядковый номер патча gl_PrimitiveID считается в рамках одного вызова glDraw*. Сами данные вершин доступны через массив структур gl_in, объявленный следующим образом:

in gl_PerVertex
{
  vec4 gl_Position;
  float gl_PointSize;
  float gl_ClipDistance[];
} gl_in[gl_MaxPatchVertices];

Этот массив индексируется от нуля до gl_PatchVerticesIn — 1. Наибольший интерес в этом объявлении представляет поле gl_Position, в котором записаны данные с выхода вершинного шейдера. Количество вершин выходного патча задаётся в коде самого шейдера глобальным объявлением:

layout (vertices = 1) out; // В данном случае задана одна вершина

и оно не обязано совпадать с количеством вершин во входном патче. Количество вызовов шейдера равно количеству выходных вершин. В каждом вызове шейдер имеет доступ ко всем входным вершинам патча, но при этом имеет право записывать только по индексу gl_InvocationID выходного массива gl_out, который объявлен как

out gl_PerVertex
{
  vec4 gl_Position;
  float gl_PointSize;
  float gl_ClipDistance[];
} gl_out[];

Теперь перейдём к более интересному факту. Шейдер может записывать только по индексу gl_InvocationID, однако он может читать выходной массив по любому индексу! Мы помним, что работа шейдеров очень сильно распараллелена, и порядок их вызова не детерминирован. Это накладывает ограничения на совместное использование данных шейдерами, но делает возможным SIMD-параллелизм и даёт компилятору карт-бланш на использование самых суровых оптимизаций. Чтобы эти правила не нарушались, в шейдере управления тесселяцией доступна барьерная синхронизация. Вызов встроенной функции barrier() блокирует исполнение до тех пор, пока все шейдеры патча не вызовут эту функцию. На вызов этой функции наложены серьёзные ограничения: её нельзя вызывать из любой функции, кроме main, её нельзя вызывать ни в одной конструкции управления потоком (for, while, switch), и её нельзя вызывать после return.

И, наконец, самое интересное на этой стадии конвейера: выходные данные вершин — не главное. Полигоны будут собираться не из координат, записанных в gl_out. Основным продуктом шейдера управления тесселяцией является запись в следующие выходные массивы:

patch out float gl_TessLevelOuter[4];
patch out float gl_TessLevelInner[2];

Эти массивы управляют количеством вершин в так называемых абстрактных патчах, и именно поэтому данная стадия называется управлением тесселяцией. Абстрактный патч — это набор точек двумерной геометрической фигуры, который генерируется на стадии tessellation primitive generation. Абстрактные патчи бывают трёх видов: треугольники, квадраты и изолинии. При этом для каждого вида абстрактного патча шейдер должен заполнить только нужные ему индексы gl_TessLevelOuter и gl_TessLevelInner, а остальные индексы этих массивов игнорируются. Генерируемый патч содержит не только вершины геометрической фигуры, но и координаты точек на границах и внутри фигуры. Например, квадрат при некоторых значениях gl_TessLevelOuter и gl_TessLevelInner будет сформирован из треугольников такого вида:

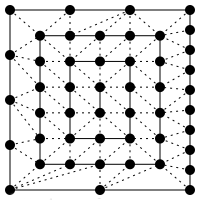
Левый нижний угол квадрата всегда имеет координату [0; 0], правый верхний — [1; 1], а все остальные точки будут иметь соответствующие координаты со значениями от 0 до 1.

Изолинии — это по сути тоже квадрат, разбитый на прямоугольники, а не на треугольники. Значения координат точек на изолиниях так же будут принадлежать интервалу от 0 до 1.

А вот координаты внутри треугольника устроены принципиально по-другому: в двумерном треугольнике используются трёхкомпонентные барицентрические координаты. При этом их значения так же лежат в отрезке от 0 до 1, а треугольник является равносторонним.

Конкретный вид разбиения (которое, собственно, и называется тесселяцией в изначальном смысле) абстрактного патча сильно зависит от gl_TessLevelOuter и gl_TessLevelInner. Мы здесь не будем останавливаться на нём подробно, как и не будем разбирать чем Inner отличается от Outer. Всё это подробно изложено в соответствующем разделе руководства по OpenGL.

Теперь вернёмся к нашим растениям. На данном этапе графического конвейера мы ещё не можем выполнить какие-либо осмысленные преобразования над имеющейся единственной точкой, поэтому на выход этого шейдера подадим входную вершину без изменений:

gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;

Для генерации геометрии мы будем использовать прямоугольную решётку, то есть абстрактный патч типа «изолинии». Генерация изолиний управляется только двумя переменными: gl_TessLevelOuter[0] — количество точек по координате y, и gl_TessLevelOuter[1] — количество точек по x. В нашей программе цикл по y будет пробегать по стеблям куста, а для каждого стебля цикл по x будет пробегать вдоль стебля. Поэтому количество стеблей (четвёртую координату входной точки) мы записываем на соответствующий выход:

gl_TessLevelOuter[0] = gl_in[gl_InvocationID].gl_Position.w;

Количество точек вдоль стебля определяет количество отрезков, из которых стебель составлен, то есть его детализацию. Дабы не тратить ресурсы впустую, сделаем уровень детализации зависимым от расстояния между камерой и кустом:

uniform vec3 eyePosition; // Положение камеры передаётся в эту переменную из объекта камеры.
int lod() {
    // Расстояние от камеры до куста:
    float dist = distance(gl_in[gl_InvocationID].gl_Position.xyz, eyePosition);
    // Количество точек на стебле в зависимости от расстояния:
    if(dist < 10.0f) {
        return 48;
    }
    if(dist < 20.0f) {
        return 24;
    }
    if(dist < 80.0f) {
        return 12;
    }
    if(dist < 800.0f) {
        return 6;
    }
    return 4;
}

Со стороны CPU перед каждым вызовом glDraw* заполняются однородные переменные:

grassShader.setUniformValue("eyePosition", camera.getPosition());
grassShader.setUniformValue("lookDirection", camera.getLookDirection());

Первая из них — это координаты камеры в пространстве, а вторая — направление взгляда. Зная положение камеры, направление взгляда и координату куста, мы можем узнать, находится ли этот куст позади камеры:

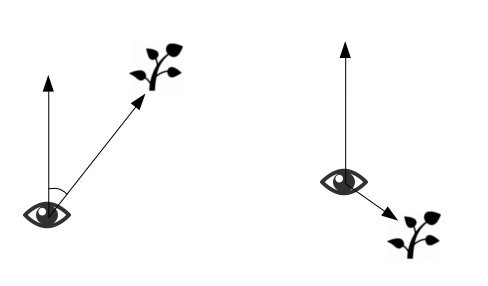
Если куст находится спереди, то угол между направлением из камеры вперёд и из камеры на куст будет острым, в противном случае — тупым. Соответственно, в первом случае скалярное произведение изображённых на рисунке векторов будет больше нуля, а во втором — меньше. Вычислим скалярное произведение и воспользуемся функцией step со ступенькой в нуле, чтобы получить переменную, которая равна нулю, если куст позади и единице если он спереди:

float halfspaceCull = step(dot(eyePosition - gl_in[gl_InvocationID].gl_Position.xyz, lookDirection), 0);

Наконец, мы можем записать количество точек для стеблей будущего куста:

gl_TessLevelOuter[1] = lod() * halfspaceCull;

Шейдер тесселяции

Замечание о терминологии: в английском оригинале этот шейдер называется Tesselation evaluation shader. В русском интернете можно найти дословные переводы вроде «шейдер оценки тесселяции» или «шейдер вычисления тесселяции». Они выглядят неуклюже и, на мой взгляд, не отражают суть этого шейдера. Поэтому здесь tesselation evaluation shader будет называться просто шейдером тесселяции, в отличие от предыдущей стадии, где был шейдер управления тесселяцией.

Тесселяция включается только если в шейдерную программу добавлен шейдер тесселяции. При этом шейдер управления тесселяцией не является обязательным: его отсутствие равносильно подаче входного патча на выход без изменений. Значения массивов gl_TessLevel* при этом можно задать со стороны CPU вызовом glPatchParameterfv с параметром GL_PATCH_DEFAULT_OUTER_LEVEL или GL_PATCH_DEFAULT_INNER_LEVEL. В этом случае все абстрактные патчи в шейдере тесселяции будут одинаковыми. Добавление в программу только шейдера управления тесселяцией не имеет смысла и приводит к ошибке компоновки шейдера. Вид абстрактного патча, в отличие от его параметров, определяется в коде шейдера тесселяции:

layout(isolines, equal_spacing) in; // В нашем случае это изолинии.

Шейдер тесселяции вызывается для каждой точки абстрактного патча. Например, если мы заказали изолинии с точками 64х64, то шейдер будет вызван 4096 раз. На его вход поступают все вершины с выхода шейдера управления тесселяцией:

in gl_PerVertex
{
  vec4 gl_Position;
  float gl_PointSize;
  float gl_ClipDistance[];
} gl_in[gl_MaxPatchVertices];

а так же уже знакомые нам gl_PatchVerticesIn, gl_PrimitiveID, gl_TessLevelOuter и gl_TessLevelInner. Две последние переменные имеют тот же самый тип, что и в шейдере управления тесселяцией, но доступны только на чтение. Наконец, самая интересная входная переменная — это

in vec3 gl_TessCoord;

В ней находятся координаты текущей (для данного вызова) точки абстрактного патча. Она объявлена как vec3, однако gl_TessCoord.z имеет смысл только для треугольников. Чтение этой координаты для квадратов или изолиний не определено.

На выход шейдера можно подать несколько переменных. Главная из них — vec4 gl_Position, в которую нужно записывать координаты вершин, из которых будут собраны примитивы для следующей стадии конвейера. В нашем случае это последовательность отрезков, т.к. шейдер тесселяции изготавливает только скелет для будущего куста.

Итак, у нас есть много (вплоть до 4096) вершин абстрактного патча, организованных в линии, которые разбиты на равные отрезки. Если мы отрисуем эту фигуру в виде линий без изменений:

gl_Position = vec4(gl_TessCoord.xy, 0.0f, 1.0f);

то увидим нечто, похожее на картинки в документации:

Здесь и далее на скриншотах вид немного сбоку

Как же сделать из этих линий стебли? Для начала поставим их вертикально:

gl_Position = vec4(gl_TessCoord.yx, 0.0f, 1.0f);

и научимся располагать их по кругу, поворачивая вокруг вертикальной оси:

vec3 position = vec3(2.0f, gl_TessCoord.x, 0.0f);
float alpha = gl_TessCoord.y * 2.0f * M_PI;
float cosAlpha = cos(alpha);
float sinAlpha = sin(alpha);
mat3 circDistribution = mat3(
    cosAlpha, 0.0f, -sinAlpha,
    0.0f,     1.0f,      0.0f,
    sinAlpha, 0.0f, cosAlpha);
position = circDistribution * position;
gl_Position = vec4(position, 1.0f);

Однако, такие линии больше похожи на забор, чем на куст. Чтобы сделать наш куст натуральнее, давайте изогнём линию как кубическую кривую Безье:

И здесь очень пригодится координата gl_TessCoord.x, про которую мы условились думать, что она пробегает вдоль каждого стебля от нуля до единицы. Вид кривой полностью зависит от опорных точек P₀… P₃. Низ стебля у нас всегда будет располагаться на земле, а его верх должен обязательно смотреть в сторону неба, поэтому примем P₀ = (0; 0). А для выбора хотя бы приблизительного положения оставшихся свободных точек прекрасно подойдёт сайт cubic-bezier.com, единственной целью которого является построение кривой требуемого вида. Теперь если gl_TessCoord.x подставить в формулу кривой Безье, то получится ломаная, вершины которой лежат на кривой, а отрезки аппроксимируют кривую:

float t = gl_TessCoord.x; // Параметр кривой.
float t1 = t - 1.0f; // Для удобства используем параметр, проходящий от корня к вершине стебля.
// Кривая Безье:
position.xy = -p0 * (t1 * t1 * t1) + p3 * (t * t * t) + p1 * t * (t1 * t1) * 3.0f - p2 * (t * t) * t1 * 3.0f;
// Отодвигаем стебель от начала координат, чтобы все стебли не росли из одной точки:
position.x += 2.0f;
// Строим стебель в вертикальной плоскости. За поворот по кругу отвечает код, приведённый выше:
position.z = 0.0f;

В дальнейшем нам понадобится наращивать полигоны вокруг искривлённого стебля, для чего в каждой вершине ломаной стебля нужно знать плоскость, перпендикулярную к стеблю. Из курса дифференциальной геометрии известно, что вектор главной нормали к параметрической кривой можно получить как комбинацию векторных произведений производных кривой по параметру:

[B', [B', B'']] (1)

Для однозначного задания плоскости нам нужен ещё один вектор. В нашем случае вся кривая расположена в вертикальной плоскости XY, а значит главная нормаль к расположена в ней же. Поэтому бинормаль к кривой достаётся нам даром — это всего лишь постоянный вектор (0; 0; 1). Теперь мы вспоминаем, что из уютной плоскости XY стебель поворачивается вокруг начала координат, а значит и нормальную плоскость тоже надо повернуть. Для этого достаточно умножить оба её образующих вектора на ту же матрицу поворота, что и точки стебля. Собираем всё воедино:

// Глобальные объявления:
out vec3 normal;
out vec3 binormal;
// Нормаль:
normal = normalize(
circDistribution * // Матрица поворота, определённая в коде выше.
vec3( // Векторы нормали в вершианх ломанной, вычисленные по формуле (1):
    p0.y * (t1 * t1) * -3.0f + p1.y * (t1 * t1) * 3.0f - p2.y * (t * t) * 3.0f +
	p3.y * (t * t) * 3.0f - p2.y * t * t1 * 6.0f + p1.y * t * t1 * 6.0f,
    p0.x * (t1 * t1) *  3.0f - p1.x * (t1 * t1) * 3.0f + p2.x * (t * t) * 3.0f -
	p3.x * (t * t) * 3.0f + p2.x * t * t1 * 6.0f - p1.x * t * t1 * 6.0f,
    0.0f
));

// Бинормаль:
binormal = (circDistribution * vec3(0.0f, 0.0f, 1.0f));

И для наглядности уменьшим детализацию стеблей. Нормали отрисованы красным, а бинормали — синим:

Теперь коротко об анимации. Во-первых, стебли шевелятся сами по себе. Это сделано через круговое вращение опорных точек кривой вокруг других, первоначальных точек. При этом положение первоначальных точек и начальная фаза вращения зависят от случайной величины (помните случайную одномерную текстуру?), которая, в свою очередь, зависит от gl_TessCoord.y и gl_PrimitiveID. Таким образом, каждый стебель в каждом кусте шевелится по своему, что создаёт иллюзию хаоса. А так как шевеление сделано через передвижение опорных точек, то нормали и бинормали остаются полностью корректными. По сути, у нас получилась скелетная анимация, у которой кости генерируются налету, а не занимают память.

Кроме собственного шевеления кустов, на них ещё воздействует «ветер». Ветер — это смещение вершин стебля в заданном пользователем направлении на величину, которая зависит от двух пользовательских параметров и шума Перлина. При этом ветер не должен смещать корни стеблей, поэтому величина смещения умножается на функцию гибкости:

float flexibility(const in float x) {
    return x * x;
}

взятую от координаты вдоль стебля t1. Пользовательские параметры ветра называются «скоростью» и «турбулентностью» чисто условно, потому что их изменение в доступном пользователю диапазоне похоже на изменение этих параметров воздушного потока. Тем не менее, этот «ветер» не имеет никакого отношения к реальной физике. Ползунок скорости в интерфейсе намеренно ограничен небольшой величиной, потому что ветер применяется к скелету уже после вычисления нормалей без их корректировки. Из-за этого нормали перестают быть таковыми, и при сильном искажении скелета (большой «скорости» ветра), появляются самопересечения полигонов.

Зачем шум Перлина, если есть «шумная» текстура? Дело в том, что значения текстуры не являются непрерывной функцией от координаты, в отличие от шума Перлина. Поэтому, если в каждом кадре делать смещение, зависящее от шумной текстуры, мы получим хаотичное дёрганье с частотой кадров вместо плавного ветра. Качественная реализация шумов Перлина взята у Стефана Густавсона.

Что ещё понадобится для наращивания полигонов? Во-первых, толщина стебля должна уменьшаться от корня к верхушке. Поэтому заведём соответствующую выходную переменную и передадим в неё толщину, зависящую от координаты вдоль стебля:

out float stemThickness;
float thickness(const in float x) {
    return (1.0f - x) / 0.9f;
}
//...
stemThickness = thickness(gl_TessCoord.x);

Саму координату вдоль стебля и номер стебля в кусте тоже передадим дальше по конвейеру:

out float along;
flat out float stemIdx;
// ...
along = gl_TessCoord.x;
stemIdx = gl_TessCoord.y;

Они понадобятся нам при наложении текстуры.

Геометрический шейдер

Наконец мы подошли к завершению геометрической части нашего пути. На вход геометрического шейдера мы получаем примитивы целиком. Если на входе стадии тесселяции были произвольные патчи, которые могли содержать приличное количество данных, то здесь примитивы — это точки, линии, либо треугольники. Если шейдеры тесселяции отсутствуют, то на вход геометрического шейдера появляются примитивы (как правило, треугольники) из вызова glDraw*, которые, возможно, было повершинно обработаны вершинным шейдером. В нашем же случае тесселяция выдаёт изолинии, которые мы принимаем в виде отрезков, то есть пар вершин:

layout(lines) in;

Эти вершины записаны во встроенный входной массив

in gl_PerVertex
{
  vec4 gl_Position;
  float gl_PointSize;
  float gl_ClipDistance[];
} gl_in[];

который в нашем случае можно индексировать только нулём иди единицей. Пользовательские входные переменные так же определены как массивы с тем же диапазоном индексов:

in vec3 normal[];
in vec3 binormal[];
in float stemThickness[];
in float along[];
flat in float stemIdx[];

На выход геометрического шейдера можно подавать точки, последовательность линий или последовательность треугольников. Мы воспользуемся последним вариантом:

layout(triangle_strip) out;

Шейдер вызывается для каждого входного примитива и может выдать несколько примитивов. Это делается с помощью двух встроенных функций. Как и на предыдущих стадиях, выходная переменная называется gl_Position. После её заполнения шейдер должен вызвать встроенную функцию EmitVertex(), чтобы сообщить видеокарте об окончании формирования вершины. По окончании формирования всех вершин примитива вызывается функция EndPrimitive();

Полигоны стебля формируются просто: зная плоскости, перпендикулярные кривой стебля в начале и в конце отрезка, мы движемся в этих плоскостях вокруг точки пересечения с отрезком и выпускаем вершины с некоторым шагом. От этого шага зависит детализация, т.е. будет ли стебель больше похож на пирамиду или на конус.

Например, вот так выглядит куст из 5-секторных стеблей с неинтерполированными (flat) координатами и нормалями фрагментов для наглядности:

А вот код, реализующий описанный подход:

for(int i = 0; i < numSectors + 1; ++i) { // Цикл по секторам
    float around = i / float(numSectors); // Координата на окружности, отображённой на [0; 1]
    float alpha = (around) * 2.0f * M_PI; // Аргумент (угол) текущей точки на окружности
    for(int j = 0; j < 2; ++j) { // Цикл по концам отрезка
        // Радиус-вектор вершины будущего полигона относительно конца отрезка:
	vec3 r = cos(alpha) * normal[j] + sin(alpha) * binormal[j];
        // Вершина полигона в мировой системе координат:
	vec3 vertexPosition = r * stemRadius * stemThickness[j] + gl_in[j].gl_Position.xyz; 
        // Передаём координату вершины во фрагментный шейдер с интерполяцией.
        // Она понадобится для вычисления освещения.
        // Её требуется передавать через пользовательскую переменную, т.к. gl_Position отвечает
        // только за формирование полигонов, но не появляется на входе фрагментного шейдера.
	fragPosition = vertexPosition;
        // Аналогично с нормалью.
	fragNormal = r;
        // Координата вдоль стебля передаётся без изменений и будет интерполирована.
	fragAlong = along[j];
        // Координата вокруг стедля так же будет интерполирована. В совокупности
        // fragAlong и fragAround образуют систему координат на поверхности стебля, которая
        // будет использована для наложения текстуры.
	fragAround = around;
        // Фрагментный шейдер будет иметь представление о том, к какой части модели
        // принадлежит обрабатываемый фрагмент. Такой информации можно придумать
        // очень разнообразное применение.
	stemIdxFrag = stemIdx[j];
        // Наконец, запишем координату вершины с преобразованием камеры и проекции.
        // Сравните это со "старомодными" шейдерами, где аналогичное преобразование делалось
        // в вершинном шейдере для каждой вершине по отдельности.
	gl_Position = viewProjectionMatrix * vec4 (vertexPosition, gl_in[j].gl_Position.w);
	EmitVertex();
    }
}
EndPrimitive();

Фрагментный шейдер

Фрагментный шейдер выглядит довольно стандартно, поэтому расскажу о нём коротко. В нём обычное освещение по Фонгу суммируется с процедурной текстурой в виде клеток на основе диаграммы Вороного, взятой у уже знакомого нам Стефана Густавсона. Цвет «текселя» зависит не только от текстурных координат, но так же от времени (номера кадра) и от номера стебля в кусте:

out vec4 outColor;
float sfn = float(frameNumber) / totalFrames;
float cap(const in float x) {
    return -abs(fma(x, 2.0f, -1.0f)) + 1.0f;
}
//...
float cell = cellular2x2(vec2(fma(sfn, 100, rand(stemIdxFrag) + fragAlong * 3.0f),
        cap(fragAround)) * 10.0f).x * 0.3f;
outColor = ambient + diffuse + specular + vec4(0.0f, cell, 0.0f, 0.0f)

Таким образом, клетки плавно «ползут» по стеблю, выглядя разными на различных стеблях.

На этом путь данных по графическому конвейеру заканчивается, а значит самое время подвести итог.

Зачем?

Итак, что же мы выиграли по сравнению с более традиционными подходами? Ответ: память, гибкость и экономию пропускной способности. При попытке сделать анимацию аналогичной гибкости другим способом, нам пришлось бы делать что-то из этого:

• Стримить геометрию в видеопамять, а заодно и грузить центральный процессор. Это самый лобовой способ, так вряд ли кто-то делает для таких объёмов данных.
• Хранить в памяти кости и использовать геометрический шейдер. Но тогда скорее всего понадобились бы дополнительные атрибуты вершин под какие-нибудь метаданные, плюс проброс больших объёмов данных через однородные переменные.
• Пожертвовать хаотичностью анимации или добавить больше случайных величин. Это вылилось бы в большие объемы текстур со случайными данными или же в большее количество вычислений шума Перлина.

Полезные ссылки

Большая часть ссылок уже находится в тексте. Здесь я хотел бы оставить полезные ссылки, которые были использованы в ходе работы над демкой:

• Уравнение Навье-Стокса в реальном времени. Описанный по ссылке способ обсчёта поведения сплошной среды можно применить вместо рассмотренного в посте псевдо-ветра, реализовав его в вычислительном шейдере. Этот «настоящий» ветер будет завихряться и обтекать препятствия.
• Официальный краткий референс-мануал по OpenGL. Полезен при написании шейдеров, так как позволяет не забыть о существовании той или иной встроенной функции.
• Обзор программируемого конвейера.

Спасибо за внимание!

Автор: SergeySib

Источник