OpenGL-Tutorial. Урок 3. Матрицы

Предисловие

В прошлом уроке мы научились рисовать треугольник и работать с шейдерами. В этом уроке мы поговорим о важнейшей части OpenGL, да и вообще компьютерной графики. О матрицах.
Всех заинтересовавшихся, прошу под кат.

КДПВ

Карта уроков

Базовые уроки:

• Урок 1. Создание окна
• Урок 2. Первый треугольник
• Урок 3. Матрицы
• Урок 4. Цветной куб
• Урок 5. Текстурированный куб
• Урок 6. Клавиатура и мышь
• Урок 7. Загрузка моделей
• Урок 8. Базовый шейдинг

Продвинутые уроки:

• Урок 9. VBO индексация
• Урок 10. Прозрачность
• Урок 11. 2D текст
• Урок 12. OpenGL расширения
• Урок 13. Normal Mapping
• Урок 14. Отрисовка на текстуру
• Урок 15. Lightmaps
• Урок 16. Shadow mapping
• Урок 17. Вращение
• Урок 18.1. «Билборды»
• Урок 18.2. Частицы

Всякое:

• Урок 19. FPS счетчик
• Урок 20.1. Нажатие на объекты с помощью OpenGL хака
• Урок 20.2. Нажатие на объекты с помощью физического движка
• Урок 20.3. Нажатие на объекты с помощью собственного raycastingа

Статья

Двигатели не двигают корабль. Корабль остается на месте, это вселенная движется вокруг корабля.
Футурама

Это самый важный урок из всех. Прочтите его как минимум восемь раз.

Введение

Однородные координаты

До этого времени мы работали только с трехкомпонентными вершинами, такими как (x, y, z). Давайте введем w. Теперь мы будем работать с (x, y, z, w) векторами.

Скоро станет яснее, а пока запомните следующие аксиомы:

• Если w == 1, тогда вектор (x, y, z, 1) — это позиция в пространстве.
• Если w == 0, тогда вектор (x, y, z, 0) — это направление.

Так какая разница? Что же, для вращений ничего не поменялось. Когда вы вращаете точку или направление, Вы получаете один и тот же результат. А вот для перемещения, изменения появились. Что означает «подвинуть направление»? Немного бессмысленно.

Однородныекоординаты позволяют нам работать с обоими случаями векторов, используя одну математическую формулу.

Матрицы трансформации

Введение в матрицы

Матрица — это просто набор чисел с заранее известным количеством строк и столбцов. К примеру матрица 2х3 будет выглядеть так:

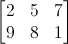
В трехмерной графике чаще всего используют матрицы 4x4. Они позволяют нам трансформировать наши 4х компонентные вершины. Делается это с помощью умножения матрицы на вершину.

Последовательность умножений важна! Матрица * Вершину = ТрансформированнаяВершина

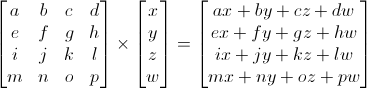
Не так страшен черт как его малюют. Приложите левый указательный палец на «a», а ваш правый указательный на «x». Это «ax». Двигайте левую руку к числу «b», а вашу правую руку к числу «y». Вы получили «by», затем «cz», затем «dw». «ax + by + cz + dw». Вот вы и получили новый «x»!
Проделайте это для каждой строки и вы получите новый (x, y, z, w) вектор.

Довольно утомительно считать все это вручную, поэтому давайте попросим компьютер сделать это за вас.

В С++, с помощью GLM:

glm::mat4 myMatrix;
glm::vec4 myVector;
// Как-нибудь заполняем матрицу и вектор
glm::vec4 transformedVector = myMatrix * myVector; // Опять же, именно в таком порядке. Это важно!

В шейдере GLSL:

mat4 myMatrix;
vec4 myVector;
// Как-нибудь заполняем матрицу и вектор
vec4 transformedVector = myMatrix * myVector; // Да, абсолютно так же как и в GLM

(Не забывайте пробовать код!)

Матрицы перемещения

Это самая простая матрица для понимания. Выглядит матрица перемещения следующим образом:

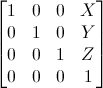
Где X, Y, Z — это значения, которые вы хотите добавить к вашей позиции.

Так что если мы хотим подвинуть вектор (10, 10, 10, 1) на 10 единиц по оси X, мы получим:

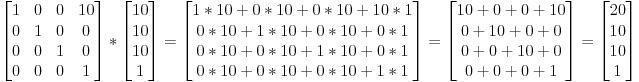
… и в результате мы получили преобразованный однородный вектор (20, 10, 10, 1)! Помните, w == 1 означает, что это позиция, а не направление. Если мы попробуем применить эту матрицу к направлению — то ничего не изменится (что хорошо):
Давайте проверим это. Что произойдет с вектором, который прдставляет направление по оси -z: (0, 0, -1, 0)

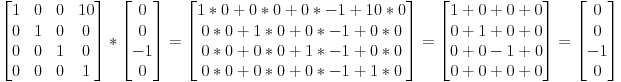
… и мы получили наше начальное направление. И это абсолютно правильно, поскольку как я и говорил ранее: движение направления смысла не имеет.
Но все таки как же нам производить перемещение в коде?

В С++ с помощью GLM:

#include <glm/gtx/transform.hpp> // после <glm/glm.hpp>
 
glm::mat4 myMatrix = glm::translate(10.0f, 0.0f, 0.0f);
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f);
glm::vec4 transformedVector = myMatrix * myVector; // угадайте результат

В шейдере GLSL:

vec4 transformedVector = myMatrix * myVector;

Фактически Вы почти никогда не будете делать этого в GLSL. Чаще всего вы будете производить перемещение в C++ коде с помощью glm::translate и результат отправлять в GLSL.

Единичная матрица

Эта матрица особенная. Она ничего не делает. Но я упомину ее, поскольку важно понимать, что умножение A на 1.0 дает A.

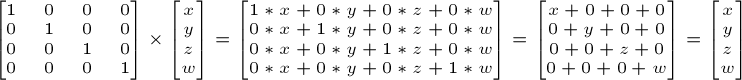
В С++ с помощью GLM:

glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

Матрицы масштабирования

Матрица масштабирования тоже довольно проста:

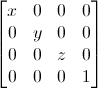
К примеру если вы хотите масштабировать вектор (не важно, позицию или направление) на 2 во всех направлениях:

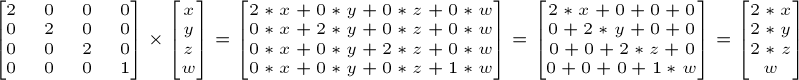
И вектор W опять не изменился. Вы можете спросить: а какой смысл в «направлении масштабирования»? Что же, чаще всего особого смысла это не несет. Но в некоторых, довольно редких случаях, это может быть полезно.

(Заметьте, что единичная матрица — это частный случай матрицы масштабирования)

В С++ с помощью GLM:

// #include <glm/gtc/matrix_transform.hpp> и #include <glm/gtx/transform.hpp>
glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

Матрицы вращения

Эти матрицы довольно сложны. Я опущу детали, поскольку не обязательно понимать всю подноготную, что бы матрицы работали. Если хотите получить больше информации, то можете взглянуть на Matrices and Quaternions FAQ (довольно популярный ресурс. Скорее всего есть на вашем языке. Хотя я на русском найти не смог). Так же вы можете взглянуть на 17 урок.

В С++ с помощью GLM:

// #include <glm/gtc/matrix_transform.hpp> и #include <glm/gtx/transform.hpp>
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );

Объединение трансформаций

Теперь мы знаем, как вращать, перемещать и масштабировать наши векторы. Теперь настало время все это соединить! Делается это умножением матриц:

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

!!! ВАЖНО !!! Именно в таком порядке! В НАЧАЛЕ масштабирование, ЗАТЕМ вращение и в КОНЦЕ перемещение. Так работают матрицы!

Использование другого порядка не дадут такой же результат. Попробуйте сами:

• Сделайте шаг вперед и поверните налево (только в компьютер не врежтесь)
• Поверните налево и сделайте шаг вперед

Собственно, последовательность, представленная ниже обычно используется игровыми персонажами и другими элементами. В начале их масштабируют, потом вращают (устанавливают направление), затем перемещают. Для примера, дана модель корабля (вращение было убрано для упрощения).

Не правильный порядок:

• Вы перемещаете корабль на (10, 0, 0). Теперь его центр на 10 единиц дальне от центра.
• Вы масштабируете корабль в 2 раза. Каждая координата отдаляется от центра на 2. В результате вы имеете большой искаженный корабль с центром в 2*10 = 20. Это не то, что вы хотели.

Правильный порядок:

• Вы масштабируете корабль в 2 раза. Вы получаете большой корабль, отцентрованный по центру.
• Вы перемещаете корабль. Он имеет такой же размер, но теперь на правильной позиции.

Умножение матрица-матрица похоже на умножение матрица-вектор, так что я опять опущу некоторые детали и отправлю вас к Matrices and Quaternions FAQ за деталями.
А теперь просто попросим компьютер произвести все умножения:

В C++ с помощью GLM:

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

В шейдере GLSL:

mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

Матрицы модели, вида и проекции

До конца этого урока мы предположим, что мы знаем, как нарисовать любимую трехмерную модель Blender: обезьяну Suzanne

Матрицы модели, вида и проекции — это инструментарий, который позволяет разделить трансформации. Вы можете не использовать их (по крайней мере мы не использовали их в 1 и 2 уроках). Но вам стоило бы. Так делают все, потому что это самый простой способ.

Матрица модели

Эта модель, так же как и наш треугольник описывается набором вершин. X, Y и Z координаты этих вершин объявлены относительно центра объекта. То есть если у вершины координаты (0, 0, 0), то она в центре объекта.

Мы бы хотели иметь возможность двигать эту модель, как минимум по причине пользовательского ввода с клавиатуры и мыши. Расслабьтесь, вы уже знаете, что надо делать: translation * rotation * scale и все. Вы применяете эту матрицу к каждой вершине в каждом кадре (В шейдере GLSL, не в C++!) и все будет движется. А все, что не движется — находится в центре мира.

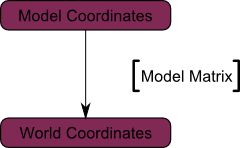
Ваши вершины теперь расположены в Мировых координатах. Это показывает черная стрелка на следующем изображении: Мы перешли от Координат модели (все вершины определены относительно центра модели) к Мировым координатам (все вершины определены относительно центра мира)

Мы можем подвести все наши действия к следующей диаграмме:

Матрица вида

Давайте снова вернемся к футураме:

Двигатели не двигают корабль. Корабль остается на месте, это вселенная движется вокруг корабля.

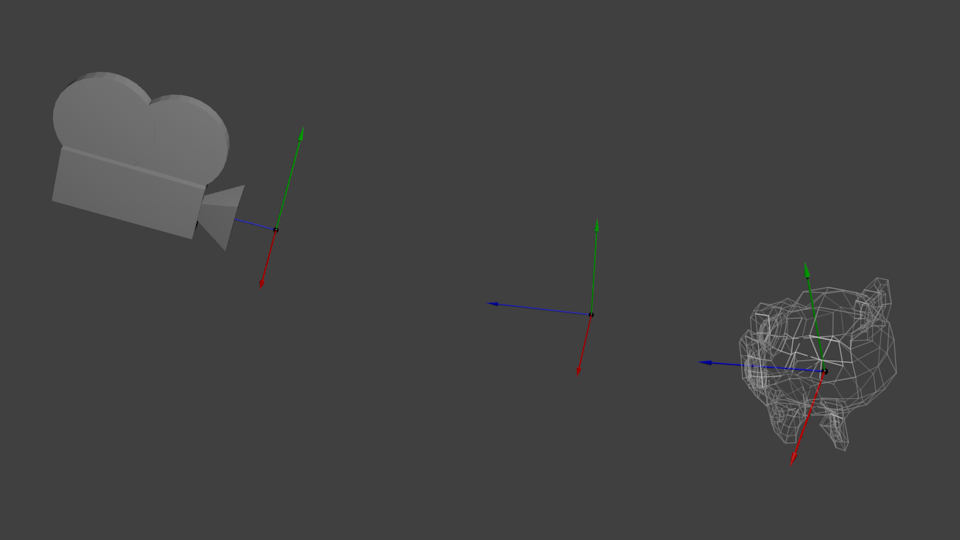
То же самое применимо и к камерам. Если вы хотете посмотреть на гору под другим углом, вы можете либо подвинуть камеру… либо подвинуть гору. Это не применимо к реальной жизни, зато отлично применимо в компьютерной графике.

По умолчанию ваша камера находится в центре Мировых координат. Для того, что бы подвинуть мир мы введем еще одну матрицу. Давайте представим, что вы хотите сместить камеру на 3 единицы направо (+X). Это эквивалентно сдвигу мира на 3 единицы ВЛЕВО (-X). Пока ваш мозг вытекает, давайте попробуем сделать это:

// #include <glm/gtc/matrix_transform.hpp> и #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(-3.0f, 0.0f ,0.0f);

Снова, изображение ниже иллюстрирует этот процесс: Мы переходим из Мировых координат (все вершины определены относительно цента мира) к Координатам камеры (все координаты определены относительно камеры).

Пока ваш мозг окончательно не взорвался, насладитель прекрасной функцией GLMа, glm::lookAt.:

glm::mat4 CameraMatrix = glm::lookAt(
    cameraPosition, // позиция камеры в мировых координатах
    cameraTarget,   // куда будет смотреть камера, в мировых координатах
    upVector        // предположительно glm::vec3(0, 1, 0), но (0, -1, 0) перевернет камеру верх-ногами, что тоже довольно весело.
);

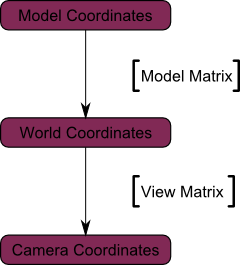
Теперь наша диаграмма выглядит следующим образом:

Но и это еще не все.

Матрица проекции

Сейчас мы находимся в Координатах камеры. Это означает, что после всех изменений вершины, координаты «x» и «y» которых были равны 0 должны быть отрисованы в центре экрана. Но мы не можем использовать только координаты «x» и «y» для определения позиции обхекта на экране. Ведь координата «z» так же учитывается. Для двух координат с одинаковыми «x» и «y», вершина с большей «z» координатой будет ближе к центру, чем вершина с меньшей «z».

Это называется «перспективной проекцией»:

К счастью матрица 4х4 может отобразить проекцию. (Ну то есть не совсем, но это не важно).

// Генерируем очень сложную для понимания матрицу. Но она также 4х4
glm::mat4 projectionMatrix = glm::perspective(
    FoV,         // Горизонтальное поле обзора, в градусах: приближение. Читай "линза камеры". [FoV - угловое пространство, видимое глазом при фиксированном взгляде и неподвижной голове. ] Обычно между 90 градусами и 30 градусами.
    4.0f / 3.0f, // Соотношение сторон. Зависит от размера окна. Заметьте, что 4 / 3 == 800 / 600 == 1280 / 960. Звучит похоже?
    0.1f,        // Ближайшая позиция плоскости отсечения. Должна быть как можно больше, иначе получите ошибки округления.
    100.0f       // Дальняя позиция плоскости отсечения. Должна быть как можно меньше.
);

И в последний раз:

Мы перешли от Координат камеры (все вершины определены относительно камеры) к однородным координатам (все вершины определены в маленьком кубе. Все, что в кубе, находится на экране).

И финальная диаграмма:

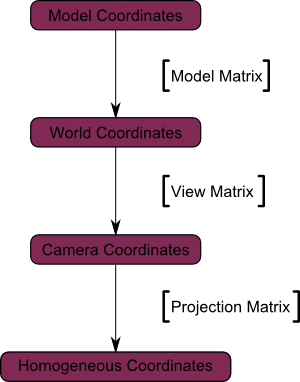
Вот другая диаграмма, которая более наглядно показывает преобразования при применении матрицы проекции. До проекции сининие объекты находятся в Координатах камеры и красная фигура показывает сечение камеры: часть сцены, которую камера на самом деле видит.

Умножение всего этого на матрицу проекции дает следующий эффект:

На этом изображении сечение камеры представляет собой идеальный куб (между -1 и 1 по всем осям), а все синие объекты были искажены определенным образом. Также объекты, которые находятся ближе к камере больше, чем объекты находящиеся дальше. Похоже на реальную жизнь!

Давайте посмотрим что видно за сечением камеры:

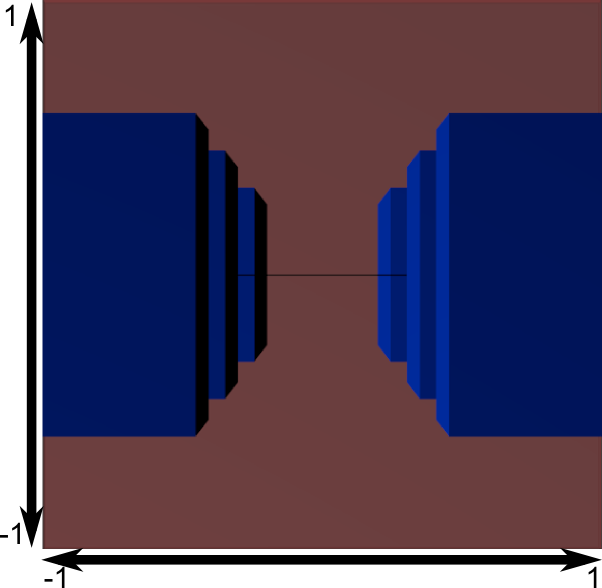
Вот и наше изображение! Но оно немного слишком квадратное, поэтому применяется еще одна транформация (она применяется автоматически и не требует никаких действий в шейдере), что бы наше изображение было в пору нашему окну:

И вот оно, отрисованное изображение!

Соединение трансформаций: Матрица ModelViewProjection

… это просто стандартное перемножение матриц, которое вы так полюбили!

// C++ : вычисление матрицы
glm::mat4 MVPmatrix = projection * view * model; // Помните: наоборот !

// GLSL : применение этой матрицы
transformed_vertex = MVP * in_vertex;

Объединение всего вместе

• 1 шаг. Генерируем нашу MVP матрицу. Это надо делать для каждой модели, которую вы отрисовываете.

  // Матрица проекции : 45° ширина обхора, соотношение сторон 4:3, промежуток отображение: 0.1 единиц <-> 100 единиц
  glm::mat4 Projection = glm::perspective(glm::radians(45.0f), (float) width / (float)height, 0.1f, 100.0f);
    
  // Или для ортогональной матрицы:
  //glm::mat4 Projection = glm::ortho(-10.0f,10.0f,-10.0f,10.0f,0.0f,100.0f); // В мировых координатах
    
  // Матрица камеры
  glm::mat4 View = glm::lookAt(
      glm::vec3(4,3,3), // Камера находится на (4, 3, 3) в мировых координатах
      glm::vec3(0,0,0), // и смотрит в центр мира
      glm::vec3(0,1,0)  // Верх - сверху (установите на (0, -1, 0), что бы смотреть сверху вниз)
      );
    
  // Матрица модели: единичная матрица, поскольку модель будет в центре
  glm::mat4 Model = glm::mat4(1.0f);
  // Наша ModelViewProjection является умножением 3 матриц
  glm::mat4 mvp = Projection * View * Model; // Помните, что матрицы перемножаются в обратном порядке
  

• 2 шаг. Предаем MVP в GLSL

  // Получаем идентификатор для нашей постоянной "MVP" 
  // Только в процессе инициализации
  GLuint MatrixID = glGetUniformLocation(program_id, "MVP");
    
  // Отправляем нашу трансформацию текущему шейдеру в постоянную "MVP"
  // Это делается в главном цикле, поскольку для каждой модели своя MVP (по крайней мере M)
  glUniformMatrix4fv(mvp_handle, 1, GL_FALSE, &mvp[0][0]);
  

• 3 шаг. Использовать MVP в GLSL для изменения наших вершин.

  // Входные данные о вершине. Значение разное при каждом выполнении шейдера.
  layout(location = 0) in vec3 vertexPosition_modelspace;
    
  // Значение, остающееся одним для всей модели
  uniform mat4 MVP;
    
  void main(){
    // Выводим новую позицию вершины: MVP * position
    gl_Position =  MVP * vec4(vertexPosition_modelspace,1);
  }
  

• Вот и все! Это все тот же треугольник, что и во 2 уроке. Все еще в на позиции (0, 0, 0), но наблюдается в перспективной проекции из точки (4, 3, 3) с углом обзора в 45 градусов.

В шестом уроке Вы научитесь изменять все эти значения динамически с помощью клавиатуры и мыши, но в начале нам надо будет придать нашим моделям немного цвета (Урок 4) и текстур (Урок 5).

Упражнения

• Попробуйте поменять значения в glm::perspective
• Используйте вместо перспективной проекции, ортогональную (glm::ortho)
• Поменяйте значения перемещения, вращения и масштабирования
• Измените последовательность умножений матриц

Автор: Megaxela

Источник