На днях была выпущена уже вторая бета-версия Криты 2.9. Этой статьей я хотел бы начать рассказ о том новом функционале, который ждет пользователей в предстоящем релизе.
Одной из самых интересных функций этого релиза является преобразование клеткой. Оно позволяет изменять форму объектов без внесения искажений в изображение. О нем и пойдет сегодня речь…

Координаты Грина
Изначально интерес к инструментам преобразования клеткой возник как к средствам трансформации трехмерных объектов. Обычно такая «клетка» представляла собой многогранник с небольшим количеством полигонов, в который заключался интересующий объект. Передвигая вершины многогранника, пользователь мог деформировать выбранный объект, получая требуемые изгиб и форму. В нашем случае мы работаем не с трехмерными моделями, а с плоскими изображениями, поэтому задача сильно упрощается: клетка становится обычным многоугольником, а деформируемый объект — набором пикселей внутри его. Манипулируя вершинами этого многоугольника, можно получать требуемые деформации изображения.
Существует множество способов задания такой клетки, но большинство из них сводятся к выражению координат каждого пиксела внутри клетки через взвешенную сумму координат вершин этой самой клетки. Полученные веса впоследствии используются для расчета нового положения пикселов после перемещения пользователем узлов клетки. Этот метод прост и понятен, однако у него есть один существенный недостаток: при его использовании сильно страдает форма объекта из-за наличия сдвиговых деформаций (преобразование не обладает свойством конформности).
Чтобы обойти этот недостаток, разработчики из университета Тель-Авива придумали другой способ. Дабы избавиться от сдвиговых деформаций и сохранить форму объекта, они предложили использовать для расчета координат пикселов не только координаты вершин клетки, но и ориентацию нормалей ее ребер. Полученные координаты получили название координат Грина в честь теории функций Грина, используемых при выводе.
Ниже приведено сравнение разных методов преобразования клеткой: a) исходное изображение; b) преобразование с использованием координат Грина; c) классический метод гармонических координат. Источник: [1]
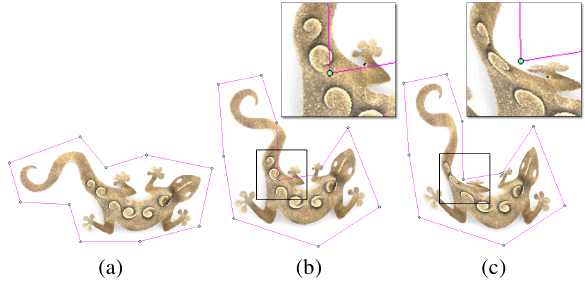
Метод с использованием координат Грина обладает множеством приятных свойств:
- он позволяет получить явные выражения для новых координат пикселов, т.е. нам не требуется решать уравнения или использовать другие итеративные методы
- так же как и другие «клеточные» алгоритмы он работает в две стадии, разделенные во времени: на первой стадии рассчитываются координаты Грина для каждого пиксела изображения с учетом начальной конфигурации клетки, а на второй полученные координаты просто перемножаются на модифицированные пользователем значения координат вершин и реберных нормалей новой клетки. Таким образом, первую стадию, самую ресурсоемкую, требуется просчитывать лишь один раз, вначале работы, а все последующие модификации будут пересчитываться быстрым алгоритмом
- в отличие от всех остальных алгоритмов, координаты Грина обладают свойством конформности, т.е. отображение любой точки изображения можно представить в виде перемещения и поворота, при этом в полученном отображении будут отсутствовать сдвиговые деформации (shear). Это означает, что любая бесконечно малая окружность будет трансформирована в окружность, а не в эллипс, как бы это произошло с обычными методами
Реализация в Крите и проблемы
При реализации алгоритма в Крите разработчики столкнулись с некоторыми интересными особенностями алгоритма. Как уже было сказано выше, по изначальной задумке авторов преобразование разделялось на две стадии, первая из которых, медленная, должна была считаться лишь один раз при инициализации инструмента, а вторая, быстрая, при каждой модификации клетки пользователем. Проблема в том, что «быстрая» стадия алгоритма оказалась не такой уж и быстрой. Преобразование объектов реальных размеров (> 2k пикселов по длинной стороне) занимало несколько секунд, поэтому в результате, поверх оригинального алгоритма была добавлена интерполяция. Изображение разбивается сеткой с шагом 8 пикселов, значения координат Грина считаются для ее узлов, а остальные пикселы интерполируются. Как выяснилось, для реальных изображений, разница практически незаметна.

Pepper and Carrot by David Revoy
Выводы и планы на будущее
Трансформация клеткой уже доступна в последних сборках Криты 2.9 Beta2. Вместе с переписанным инструментом Деформация (Warp Transform) она позволяет изменять позу и мимику двумерного персонажа без дополнительного создания и привязывания скелета.
Однако кроме базового алгоритма, у трансформации клеткой есть еще интересное расширение. Сейчас изменение всего одной вершины способно привести к изменениям всей выделенной области, причем даже в тех частях, которые находятся на другой стороне картинки. Это не всегда удобно, т.к., чтобы изменить, например, руку персонажа потребуется занести его в клетку целиком (см. видео). Для исправления этой ситуации существует метод, позволяющий закреплять выделенные ребра клетки и редактировать части персонажа отдельно. Это как раз и будет темой для будущей работы разработчиков!
Бета-версию Криты 2.9 под Windows и Linux можно скачать на официальном сайте проекта :)
В заключение видео о том, как создавалась заглавная иллюстрация:
Автор: dkazakov-dev






