Некоторое время назад я рассказывал о программном комплексе для выявления скрытого параллелизма в произвольном алгоритме и технологиях его, параллелизма, рационального использовании (https://habr.com/ru/post/530078/). Одним из компонентов этого комплекса является т.н. “универсальный вычислитель”, выполненный в соответствии с архитектурой Data-Flow (далее DF, пото́ковый вычислитель, описание здесь https://habr.com/ru/post/534722/).
В результате обдумывания особенностей выполнения потоковых программ мне пришло в голову написать о интереснейшем (незавершённом!) этапе технологического прогресса человечества в области информационных технологий – развитии техники реализации усло́вного выполнения вычислений. Без наличия усло́вности вычислений труднопредстави́ма реализация современных программ любой парадигмы и уровня сложности.
После краткого э́кскурса в историю будет рассказано о реальном применении предикатного подхода к реализации условности выполнения операторов в (ранее упомянутом) программном симуляторе DF-вычислителя.
Идея условности выполнения некоторой части программного кода формально была озвучена Джоном (Яношом Лайошом) фон Нейманом в 1945 году в (вызвавшем немало нареканий со стороны работавших с автором исследователей) отчёте “ The First Draft Report on the EDVAC”. Ниже приводятся основные принципы архитектуры фон Неймана (она же Принстонская), текст приводится в во́льном изложе́нии:
-
Двои́чного кодирования (применение двои́чной системы счисле́ния).
-
Однородности кодирования (команды и данные хранятся в единой памяти, причём и те и другие могут быть модифицированы одинаковым образом). Гарвардская архитектура предполагает наличие двух пулов памяти – для команд и данных.
-
Адресу́емости памяти (процессору в произвольный момент доступна любая из ячеек основной памяти по её номеру - адресу).
-
Последовательного программного управления (команды располагаются в памяти и выполняются последовательно - одна после завершения другой).
-
Условного перехода (команды могут выполняться не только последовательно, но и в зависимости от состояния данных – т.е. фактически постулируется наличие команд условного перехода).
Похоже, Янош Лайош прекрасно понимал (ибо соответствующее упоминание более чем кратко и выполнено в форме дополнения к одной из б́азисной идей – концепции последовательного программного управления), что последний принцип был прекрасно известен ещё Чарльзу Бэббиджу и сотрудничающей с ним Аде Августе Байрон-Лавлейс - единственной “дочерью дома и сердца” великого поэта). В идиоматике фон Неймана условность выполнения реализовывалась путём перехода к иной (относительно следующей при последовательном выполнении) точке памяти, причём механизм этого перехода вряд ли был интересен самому автору.
Конкретную последовательность действий по “переходу к новой точке памяти” разработчикам пришлось реализовывать “по месту”. Прошли десятилетия, пока технология “устака́нилась”. Пожалуй, наиболее документированной является технология, применяемая в процессорах фирмы Intel Corp.
Ниже приведена (наби́вшая оско́мину всем, кому довелось изучать архитектуру вычислительных систем) классическая структура процессора i8086 от 1978 г. архитектуры фон Неймана с конкретизацией технологии условного выполнения машинных команд (фирма Intel Corp.).
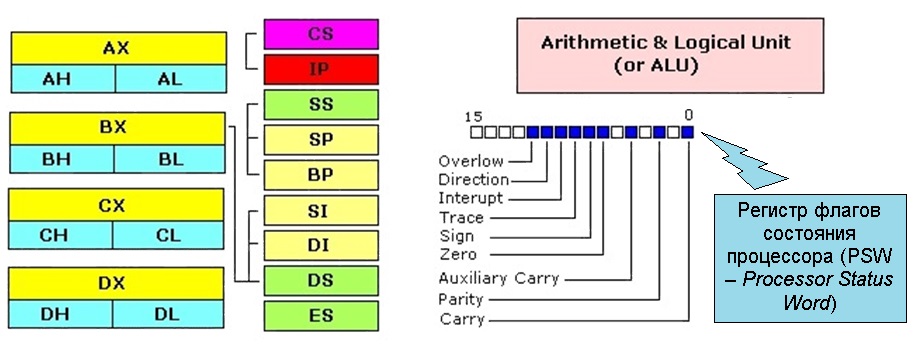
Механизм условного выполнения реализуется в полном соответствие с “указаниями” фон Неймана и включает регистр флагов состояния процессора, регистр - счётчик команд и набор обслуживающих машинных команд (мнемоника которых обычно начинается с символа ‘J’ – от “jump”, “прыжок”, “переход”). Набор битов кодов условий регистра флагов состояния процессора выбран так, что позволяет выявлять все ситуации, необходимые для корректной организации процесса вычислений.
Последовательность выполнения условного (включает и безусловный как вариант) перехода представляет собой двухстадийный процесс (в 32- и 64-битных системах используются дополнительные регистры, но общий принцип не изменяется):
-
Каждая вы́полнившаяся арифметико-логическая машинная команда определённым образом модифицирует биты кодов условий регистра состояния процессора (PSW – Processor Status Word), устанавливая или сбрасывая соответствующие его биты (напр., бит Zero устанавливается/сбрасывается при результате выполнения команды 0 или #0 соответственно, бит Parity указывает на чётность/нечётность результата операции etc).
-
Следующая далее команда перехода анализирует состояние соответствующего ей PSW-бита и заданным образом модифицирует (увеличивает или уменьшает) содержимое регистра – счётчика команд (IP, Instruction Pointer), всегда содержащий адрес в оперативной памяти (обычно в форме смещения относительно некоторого ба́зового адреса) начала следующей до́лженствующей быть исполненной машинной инструкции.
Первая часть процесса выполняется в любом случае, вторая обычно игнорируется (при последовательном выполнении инструкций счётчик команд инкрементируется на число байт длины выполненной команды автоматически (так реализуется “4-й принцип фон Неймана” из вышеприведённого списка).
Описанный механизм хорошо работал два десятка лет, но в конце XX века при попытках дальнейшего увеличения быстродействия вычислителей путём увеличения тактовой частоты начал сказываться сформулированный лордом Рэлеем в 1871 г. фундаментальный закон, согласно которому (в применимости именно к процессорам) мощность их тепловыделения пропорциональна четвёртой степени тактовой частоты процессора (увеличение частоты вдвое повышает тепловыделение в 16 раз). Современные конструкции микропроцессоров обладают рядом неприятных особенностей (ма́лая площадь теплоотдачи и возможность отда́чи тепла только с одной плоскости), ограничивающие эффективное охлаждение при выделяемой мощности (TDP, Thermal Design Power) пределом 150-200 ватт.
Решение нашлось (технология на рубеже XXI позволяла) в разработке многоядерных процессоров, при этом закон тепловыделения трансформировался в линейную зависимость от числа параллельных вычислителей (при сохранении тактовой частоты).
При относительно небольшом количестве процессорных ядер классическая технология обеспечения условности выполнения частей программы не претерпела изменений (каждое ядро получило весь набор регистров). Но начали разрабатываться процессоры с десятками/сотнями и бо́льшим числом ядер – вот тогда стало понятно, что идея снабжать каждое ядро полным набором регистров является анахронизмам.
Пришлось обратиться к иным идеям. Специалисты знают, что чуть ранее “эпохи i8086” фирма ARM (Advanced RISC Machine, иногда Acorn RISC Machine, Великобритания) разработала процессор фон-Неймановской архитектуры с системой команд RISC (Reduced Instruction Set Computer, “компьютер с сокращённым набором команд”).
Одной из особенностью системы команд процессоров ARM является так называемая предика́ция - возможность условного исполнения команд. В то время как для других архитектур таким свойством обычно обладают только команды условных переходов, в ARM была изначально зало́жена возможность условного исполнения практически любой команды. Реализовано это добавлением в коды машинных инструкций особого 4-битового поля (предика́та); одно из его значений зарезервировано на случай безусловного выполнения, а остальные кодируют то или иное сочетание бинарных условий (флагов). Подобная модификация системы команд позволяет строить очень компактные программы (и, кстати, отказаться от ресурсно-затра́тного механизма предсказа́ния перехо́дов в серии i80x86).
В качестве иллюстрации используем сакраментальный пример “с просторов InterNet’а” вычисления наибольшего общего делителя согласно алгоритму Эвклида (вариант, основанный на вычитании), иллюстрирующий выполнение программы на Ассемблере ARM.
Исходный текст на языке C (исходные числа i и j, решение в i):
while ( i != j ) { /* ANSI C-primer */
if (i > j) i-=j
else j-=i;
}Вариант ассемблера ARM (инструкция BNE соответствует JNE в ассемблере для Intel):
loop CMP Ri, Rj ; set condition “NE” if (i != j),
; "GT" if (i > j) or "LT" if (i < j)
; “EQ” if(i = j) nothing is done
SUBGT Ri, Ri, Rj ; if "GT" (greater than), i = i-j;
SUBLT Rj, Rj, Ri ; if "LT" (less than), j = j-i;
BNE loop ; if "NE" (not equal), then goto loop (соответствует while на С)Здесь CMP, как и ожидалось, сравнивает Ri и Rj и устанавливает значение бита Z регистра состояния процессора. Команды SUBGT и SUBLT представляет собой модификации обычной SUB (целочисленное вычитание) с добавленным условий (достаточно комментариев в тексте программы). Интересно, что обработка Ri==Rj не осуществляется вообще!
Идея “проста и гениальна” – никаких команд переходов, а выполнение или про́пуск команд регулируется системой предикатов (булевых переменных, включённых в собственно код команды)! В результате процесс управления выполнением команд становится децентрализованным вместо опоры на центральное управление посредством счётчика команд. Кажется, при таком подходе и сам счётчик команд не особенно нужен (а ведь именно он вызывал проблемы при параллельном выполнении)…Да, имеется минус – длина кода каждой команды увеличивается (всего-то на один или несколько бит).
Естественно, при разработке фирмой Intel революционного для конца XX века процессора Itanium для реализации условного выполнения была использована система предикатов. Itanium (в варианте Itanium-2 архитектура получила название IA-64) относится к VLIW-машинам (VLIW, Very Long Instruction Word, сверхдлинное машинное слово), базируется на подходах ILP (ILP, Instruction-Level Parallelism, параллелизм на уровне команд) и EPIC (EPIC, Explicitly Parallel Instruction Computing, явный параллелизм выполнения команд). Архитектура VLIW предполагает упаковку значительного количества машинных команд последовательно в слово значительной длины (“bundle”, свя́зка), которое поступает на вход процессора и каждая команда выполняется на собственном вычислителе одновременно (параллельно, об этом говорит аббревиатура ILP). EPIC предполагает выявление параллелизма уровня ILP программным путём (уровень компилятора) и формирование VLIW из независимых по данным машинных команд (обеспечивая т.о. параллелизм их выполнения). Itanium-2 разрабатывался в расчёте на идею максимального упрощения аппаратной (естественно, за счёт усложнения программной) части для снижения стоимости без чрезмерного повышения тактовой частоты.
Автор данной публикации считает перспективным подходы EPIC (распараллеливание дело не "железа", а программной части) и ILP (значительно проще провести распараллеливание на уровне машинных команд, чем выявлять гранулы параллелизма бо́льшего размера). Важная проблема Itanium – снижение производительности на некоторых приложениях вследствие малой плотности кода (запо́лненность “связки” отдельными командами небольшая) должна достигаться разработкой рационального расписания параллельного выполнения программы (об этом публикации автора https://habr.com/ru/post/530078/ и, частично, https://habr.com/ru/post/534722/). Автору неизвестны, имеются ли подобные проблемы у отечественных VLIW-процессоров серии Эльбрус.
Далее приведём примеры простого кода, показывающего применение предикации при выполнении команд IA-64 (цитируем из “великого и могучего” Э́ндрю Стюарта Таненба́ума).
Рассмотрим простой if:
if (R1 == 0) /* ANSI C-primer */
R2 = R3;
Код на Ассемблере (классическое использование условного перехода):
CMP R1,0
BNE L1 ; eq JNE in Intel Assembler
MOV R2, R3 ; R2←R3
L1: ; it’s end !...А теперь с предикацией (допустим, имеются условные команды CMOVZ и CMOVN – копирование по условию равенства/неравенства нулю флага Z в PSW, в качестве условия-предиката выступает R1==0):
CMOVZ R2,R3,R1 ; R2←R3 if R1 eq 0
CMOVN R2,R3,R1 ; R2←R3 if R1 # 0Чуть более сложный пример использования предикации:
if (R1 == 0) { /* ANSI C-primer */
R2 = R3;
R4 = R5;
} else {
R6 = R7;
R8 = R9;
}CMP R1,0 ; Assembler with no predicate
BNE L1 ; goto L1 if R1#0
MOV R2,R3
MOV R4,R5
BR L2 ; I didn't understand should be JMP or BAL to L2
L1: MOV R6,R7
MOV R8,R9
L2: ; it’s end !...В архитектуре IA-64 все команды обладают свойством предикатного выполнения, аппаратная часть включает 64 битовых регистра предикатов, доступных всем параллельным вычислителям в связке (конкретный номер управляющего бита выбирается 6-разрядным предикатным регистром).
Окончательный пример:
If (R1 == R2) /* ANSI C-primer */
R3 = R4 + R5;
else
R6 = R4 - R5 CMP R1,R2 ; Assembler with no predicate
BNE L1
MOV R3,R4
ADD R3,R5
BR L2 ; similar to previous case
L1: MOV R6,R4
SUB R6,R5
L2: ; it’s end !...Если номер бита управляющего предиката задаётся в предикатном регистре P4, то получаем удивительно простой и изящный код (синтаксис взят у вышеупомянутого автора с минимальной доработкой, ¬<P4> означит логическое обраще́ние P4-того бита регистра предикатов):
CMPEQ R1,R2,P4 ; set P4=true if R1==R2 and vice versa
<P4> ADD R3,R4,R5 ; add if P4=true
¬<P4> SUB R6,R4,R5 ; subtract if P4=falseПредикатные команды архитектуры IA-64 очень эффективны, т.к. могут помещаться в вычислительный конвейер последовательно без каких-либо проблем и не приводят к просто́ям конвейера. При этом каждая команда физически выполняется (да́бы исключить лаку́ны на ступенях конвейера), а проверка истинности предиката происходит в самом конце конвейера перед сохранением результата (в зависимости от истинности или ложности предиката результат сохраняется в выходной регистр или пропадает).
Концептуально близкое решение использует фирма NVIDIA Corp. в своих содержащих тысячи вычислительных ядер арифметических ускорителяx – априори выполняются операторы всех возможных ветвлений в программе, но результаты сохраняются только для соответствующих заданным логическим условиям.
Однако хватит теории – посмотрим, как это работает на практике. На рис. ниже приведена копия экрана при работающем эмуляторе DF (потокового) вычислителя, упомянутого в самом начале публикации. Инсталлятор http://vbakanov.ru/dataflow/content/install_df.exe (GUI Win’32), дополнительно http://vbakanov.ru/dataflow/dataflow.htm.
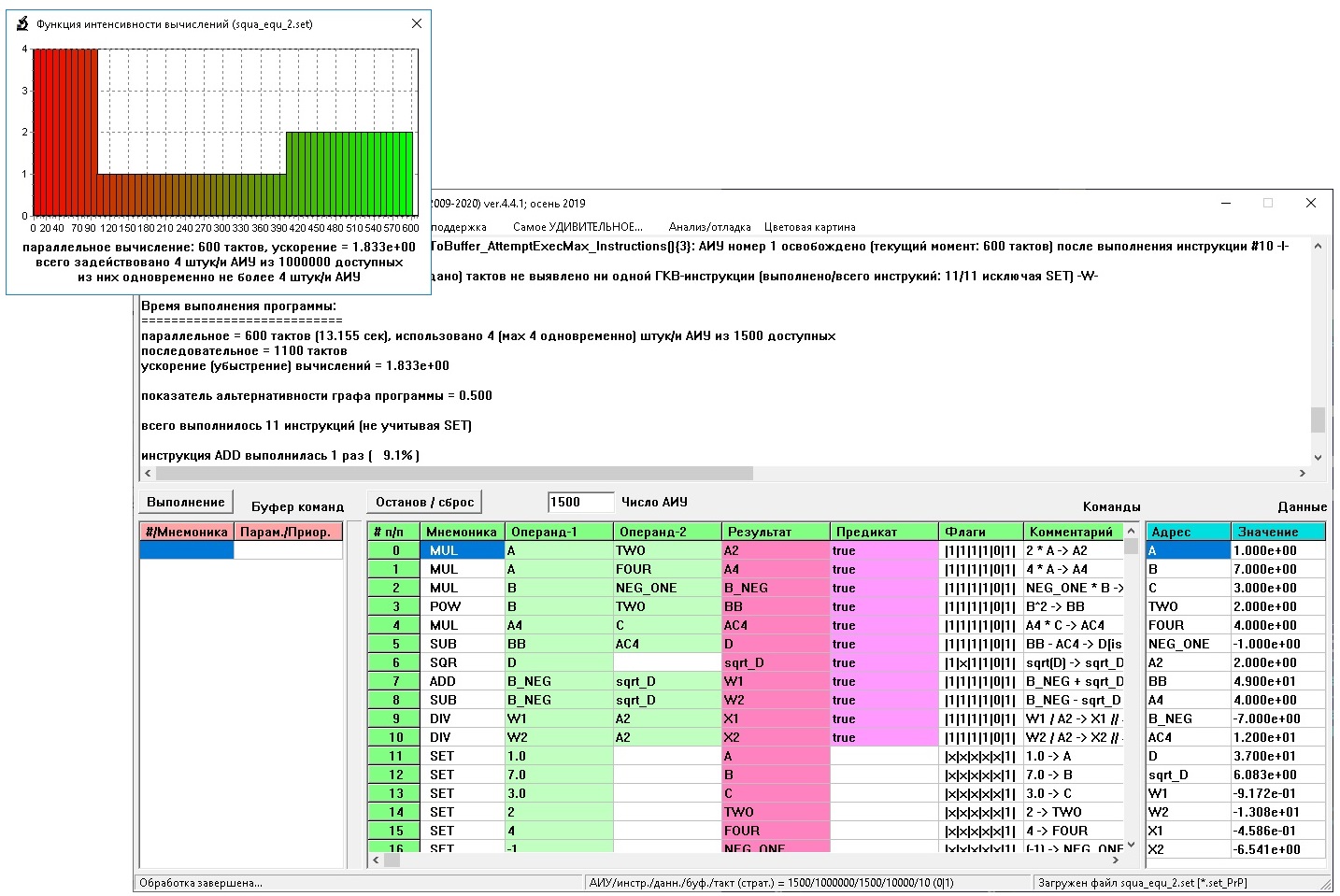
Выбор операторов для исполнения в потоковом вычислителе осуществляется по принципу “готовности к выполнению” (далее ГКВ, которая определяется “готовностью” всех операндов данного оператора – каждый операнд должен являться результатом выполнения иных операторов или быть определён простым присваиванием). ГКВ-оператор поступает на вход одного из свободных параллельных вычислителей (обычно называемых в данном случае АИУ – Арифметические Исполнительные Устройства) и на нём асинхронно относительно иных операторов выполняется, результат сохраняется в общей памяти и служит операндом для зависимых от данного операторов. DF–идеология полностью аппаратного распараллеливания (https://habr.com/ru/post/122479/) - антагонист EPIC-подхода. DF-принцип является зна́чимым расширением идиоматики фон Неймана и естественным образом реализует многие сложные понятия обработки данных. В вычислителях потоковой архитектуры процесс выбора операторов для исполнения удобно представить результатом взаимодействия множества некоторых сущностей, асинхронно выполняющих определённые действия – “актёров”, при этом натуральным образом моделируются связанные с характеристиками времени параметры обработки операторов.
Данный симулятор позволяет визуально проанализировать ход выполнения программы (для это используется отслеживающая динамику процесса вычислений цветовая гамма), получить информацию о функции интенсивности вычислений (число занятых вычислениями АИУ в каждый момент времени, см. подокно в левой верхней части копии экрана), фиксировать в файлах протокола автоматически сгенерированное DF-машиной расписание параллельного исполнения (с возможностью коррекции динамики выполнения путём управлениями приоритетами выборки из буфера ГКВ команд) при любом заданном числе гомогенных АИУ. DF-машина имеет общую память (архитектура SMP, Symmetric Multiprocessing, равно́приоритетный до́ступ всех АИУ к общей памяти).
Сам принцип DF в настоящее время ограниченно применяется фирмой Intel в своих изделиях. Начиная с модели Pentium Pro (P6, 1995 г.) процессор содержит блок DE (Dispatche/Execute Unit, устройство диспетчирования и выполнения команд), выполняющий в согласии с принципом DF ограниченное количество упрежда́юще счи́танных машинных команд. В России до своей кончи́ны в 2005 г. проблемами реализации DF-вычислителей занимался Всеволод Бурцев. Широкомасштабное применению DF в настоящее время сдерживается отсутствием производства ассоциативной памяти значительного объёма и проблемами затрат на обмен данными внутри процессора.
Укрупнённая схема DF-вычислителя приведена ниже:
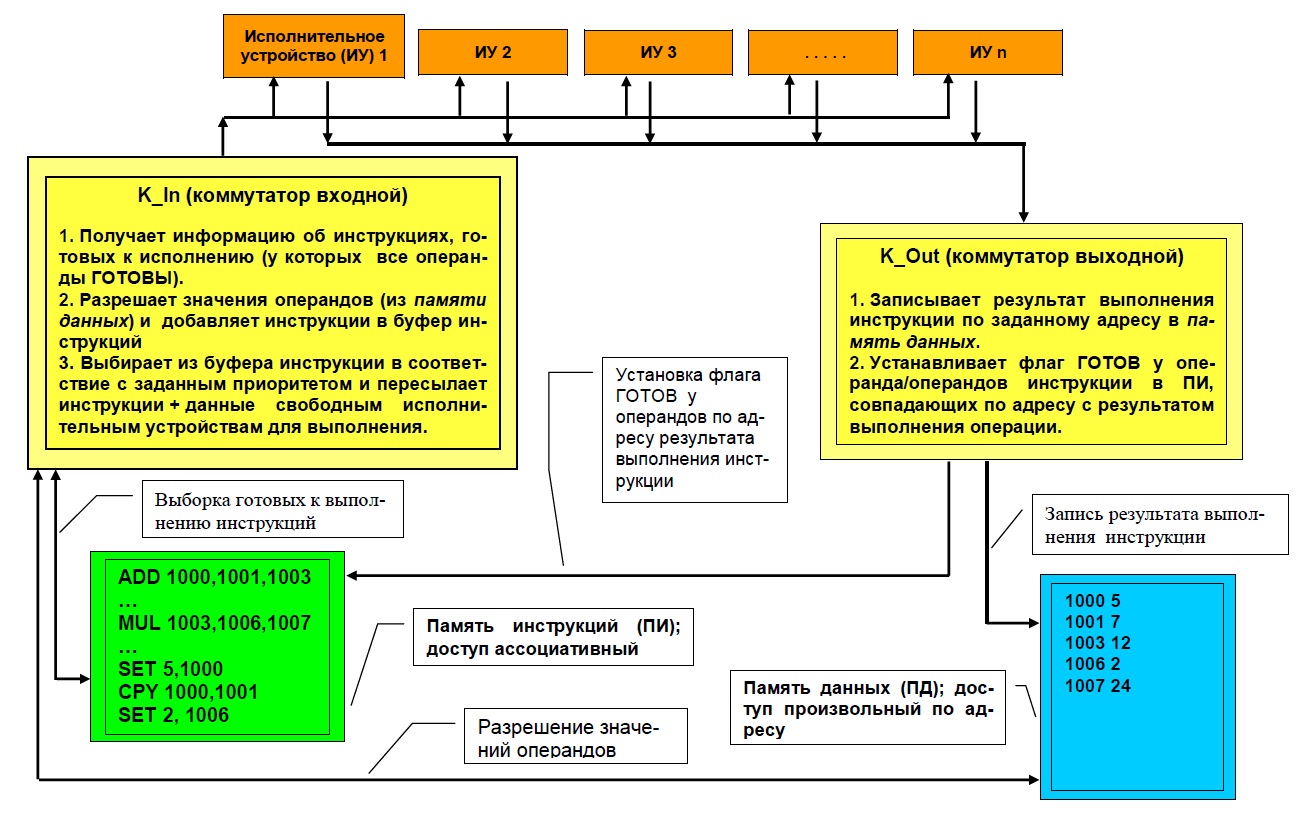
Тем не менее программная симуляция DF вполне полезна в вопросе изучения алгоритмов (в первую очередь со стороны их внутреннего параллелизма) и построения рациональных расписаний выполнения параллельных программ. Программа моделирует статическую DF машину, принцип единократного присваивания (следствие принципиальной неопределённости порядка присваивания значений одинаковым переменным) является обязательным.
DF-симулятор интерпретирует команды низкого уровня (уровня арифметико-логических операций, близких к Ассемблеру) с переменной а́дресностью (2-4), присваивание происходит в стиле AT&T (слева направо), мнемоника команд трёхсимвольная. Пример команды (время обработки каждой задаётся в настроечном файле data_flow.ini):
ADD Op_1, Op_2, Res [, Pred] ; комментарий до конца строки ,где ADD – мнемоника команды сложения, Оp1 и Оp2 – аргументы команды, Res – результат выполнения команды, Pred – необязательное имя предиката (при отсутствии считается true), перед именем предиката допускается символ отрицания ‘!’.
Т.к. здесь (в отличие от Itanium-2) нет необходимости поддержки це́лостности конвейера, вывод о необходимости или нет исполнения каждой команды принимается сразу после анализа поля предиката. Новая переменная создаётся каждый раз, когда в команде встречается неиспользованное ранее имя результата, константы задаются двухадресной командой SET.
Имя предиката не отличается от имени переменной, мнемоника предикатных команд должна начинаться с символа ‘P’, имеются все варианты условий PGE, PLE, PEQ, PGT, PLT, PNT, POR, PAN, PIM, PEV для работы с числовыми переменными и предикатами, сами предикатные функции не могут являться условно выполни́мыми):
PGT D,ZERO, IS_re_1 ; IS_re_1←true if D>ZERO
PEQ D,ZERO, IS_re_2 ; IS_re_2←true if D=ZERO
PAN IS_re_1, IS_re_2, IS_re ; IS_re←true if D>=ZEROСложные логические условия (включающие более двух параметров) обрабатывается двуместными предикатными командами последовательно. Подробное описание синтаксиса команд, особенностей выполнения и др. находится в файле base.pdf, входящем в комплекс инсталлятора http://vbakanov.ru/dataflow/content/install_df.exe.
Первый пример – получение вещественных корней полного квадратного уравнения (применение предикатов не является необходимостью):
; Решение полного квадратного уравнения (корни - вещественные числа)
; A x X^2 + B x X + C = 0
; великий индийский астроном и математик БРАХМАГУПТА (7-й век н.э.)
; in case A = 1, B = 7, C = 3
; the solve is: X1 = -0.45862 , X2 = -6.5414
;
MUL A, TWO, A2 ; А2←2×A
MUL A, FOUR, A4 ; А4←4×A
MUL B, NEG_ONE, B_NEG ; B_NEG←NEG_ONE×B
POW B, TWO, BB ; BB←B^2
MUL A4, C, AC4 ; AC4←A4×C
SUB BB, AC4, D ; D[iskriminant]←BB-AC4
SQR D, sqrt_D ; sqrt_D←sqrt(D)
;
ADD B_NEG, sqrt_D, W1 ; W1←B_NEG+D_SQRT
SUB B_NEG, sqrt_D, W2 ; W2←B_NEG-D_SQRT
DIV W1, A2, X1 ; X1←W1/A2
DIV W2, A2, X2 ; X2←W2/A2
;
SET 1.0, A ; A←2.0
SET 7.0, B ; B←7.0
SET 3.0, C ; C←3.0
;
SET 2, TWO ; TWO←2
SET 4, FOUR ; FOUR←4
SET -1, NEG_ONE ; NEG_ONE←(-1)Для решения такого же уравнения с возможностью получения комплексных корней достаточен один предикат (переменная IS_re, принимающая значение true в случае неотрицательности величины дискриминанта D уравнения; ниже имена предикатов выделены жирным шрифтом):
; Решение полного квадратного уравнения
; для получения решения в мнимых числах используем флаг предиката
; IS_re есть true при значении дискриминанта D>=0 (вещественные корни)
; A x X^2 + B x X + C = 0
; великий индийский астроном и математик БРАХМАГУПТА (7-й век н.э.)
; in case A = 1, B = 7, C = 3
; the solve is: re_X1=-0.45862,im_X1=0; re_X2=-6.5414,im_X2=0
; in case A = 1, B = 3, C = 3
; the solve is: re_X1=-1.5,im_X1=0.866; re_X2=-1.5,im_X2=-0.866
;
MUL A, TWO, A2 ; А2←2×A
MUL A, FOUR, A4 ; A4←4×A
MUL B, NEG_ONE, B_NEG ; B_NEG←NEG_ONE×B
POW B, TWO, BB ; BB←B^2
MUL A4, C, AC4 ; AC4←A4×C
SUB BB, AC4, D ; D[iskriminant]← BB - AC4
SQR D, sqrt_D, IS_re; sqrt_D←sqrt(D)
;
ADD B_NEG, sqrt_D, W1, IS_re ; W1←B_NEG + D_SQRT
SUB B_NEG, sqrt_D, W2, IS_re ; w2←B_NEG - D_SQRT
DIV W1, A2, re_X1, IS_re ; re_X1←W1 / A2
DIV W2, A2, re_X2, IS_re ; re_X2←W2 / A2
;
MUL D, NEG_ONE, NEG_D, !IS_re ; NEG_D←NEG_ONE × D
SQR NEG_D, sqrt_D, !IS_re ; sqrt_D←sqrt(NEG_D)
DIV B_NEG, A2, re_X1, !IS_re ; re_X1←B_Neg / A2
DIV sqrt_D, A2, im_X1, !IS_re ; im_X1←sqrt_D / A2
CPY re_X1, re_X2, !IS_re ; re_X2←re_X1
DIV sqrt_D, A2, W, !IS_re ; W←sqrt_D / A2
MUL W, NEG_ONE, im_X2, !IS_re ; im_X2←W × NEG_ONE
;
SET 1, A ; A←1
SET 3, B ; B←3/(or 7)
SET 3, C ; C←3
;
SET 2, TWO ; TWO←2
SET 4, FOUR ; FOUR←4
SET -1, NEG_ONE ; NEG_ONE←C(-1)
;
SET 0, ZERO ; ZERO←0
;
PGE D,ZERO, IS_re ; IS_re←true if D>=0Пример далее – поиск максимального элемента в массиве методом последовательного сравнения смежных элементов массива (элементы массива m01-m08):
; Поиск максимума в массиве с использование предикатов (выделены жирным)
; используется алгоритм последовательного сравнения чисел в массиве
;
; файл MAX-1_MASS-8.PRED.SET
;
SET 3, m01 ; первый элемент массива
SET 5, m02
SET 2, m03
SET 111, m04
SET 13, m05
SET 9, m06
SET 2, m07
SET 6, m08 ; последний элемент массива
;
PGE m02, m01, IS_02_ge_01 ; IS_02_ge_01←true if m02>=m01
CPY m02, max_01-02, IS_02_ge_01 ; if m02 >= m01
CPY m01, max_01-02, !IS_02_ge_01 ; if m02 < m01
;
PGE m03, max_01-02, IS_03_ge_max_01-02 ; IS_03_ge_max_01-02←true if m03>=max_01-02
CPY m03, max_01-03, IS_03_ge_max_01-02 ; if m03 >= max_01-02
CPY max_01-02, max_01-03, !IS_03_ge_max_01-02 ; if m03 < max_01-02
;
PGE m04, max_01-03, IS_04_ge_max_01-03 ; IS_04_ge_max_01-03←true if m04>=max_01-03
CPY m04, max_01-04, IS_04_ge_max_01-03 ; if m04 >= max_01-03
CPY max_01-03, max_01-04, !IS_04_ge_max_01-03 ; if m04 < max_01-03
;
PGE m05, max_01-04, IS_05_ge_max_01-04 ; IS_05_ge_max_01-04←true if m05>=max_01-04
CPY m05, max_01-05, IS_05_ge_max_01-04 ; if m05 >= max_01-04
CPY max_01-04, max_01-05, !IS_05_ge_max_01-04 ; if m05 < max_01-04
;
PGE m06, max_01-05, IS_06_ge_max_01-05 ; IS_06_ge_max_01-05←true if m06>=max_01-05
CPY m06, max_01-06, IS_06_ge_max_01-05 ; if m06 >= max_01-05
CPY max_01-05, max_01-06, !IS_06_ge_max_01-05 ; if m06 < max_01-05
;
PGE m07, max_01-06, IS_07_ge_max_01-06 ; IS_07_ge_max_01-06←true if m07>=max_01-06
CPY m07, max_01-07, IS_07_ge_max_01-06 ; if m07 >= max_01-06
CPY max_01-06, max_01-07, !IS_07_ge_max_01-06 ; if m07 < max_01-06
;
PGE m08, max_01-07, IS_08_ge_max_01-07 ; IS_08_ge_max_01-07←true if m08>=max_01-07
CPY m08, max_01-08, IS_08_ge_max_01-07 ; if m08 >= max_01-07 ; решение - max_01-08
CPY max_01-07, max_01-08, !IS_08_ge_max_01-07 ; if m08 < max_01-07 ; решение - max_01-08Также поиск максимального элемента в массиве методом “сдва́ивания”:
; Поиск максимума в массиве с использование предикатов (выделены жирным)
; используется алгоритм сдва́ивания
;
; файл MAX-2_MASS-8.PRED.SET
;
SET 3, m01 ; первый элемент массива
SET 5, m02
SET 17, m03
SET 234, m04
SET 13, m05
SET 9, m06
SET 2, m07
SET 6, m08 ; последний элемент массива
;
; первый этап сравнения
;
PGE m02, m01, IS_02_ge_01 ; IS_02_ge_01←true if m02 >= m01
CPY m02, max_01-02, IS_02_ge_01 ; if m02 >= m01
CPY m01, max_01-02, !IS_02_ge_01 ; if m02 < m01
;
PGE m04, m03, IS_04_ge_03 ; IS_04_ge_03←true if m04 >= m03
CPY m04, max_03-04, IS_04_ge_03
CPY m03, max_03-04, !IS_04_ge_03
;
PGE m06, m05, IS_06_ge_05 ; IS_06_ge_05←true if m06 >= m05
CPY m06, max_05-06, IS_06_ge_05
CPY m05, max_05-06, !IS_06_ge_05
;
PGE m08, m07, IS_08_ge_07 ; IS_08_ge_07←true if m08 >= m07
CPY m08, max_07-08, IS_08_ge_07
CPY m07, max_07-08, !IS_08_ge_07
;
; второй этап сравнения
;
PGE max_03-04, max_01-02, IS_0304_ge_0102
CPY max_03-04, max_01-04, IS_0304_ge_0102
CPY max_01-02, max_01-04, !IS_0304_ge_0102
;
PGE max_07-08, max_05-06, IS_0708_ge_0506
CPY max_07-08, max_05-08, IS_0708_ge_0506
CPY max_05-06, max_05-08, !IS_0708_ge_0506
;
; третий этап сравнения
;
PGE max_05-08, max_01-04, IS_0508_ge_0104
CPY max_05-08, max_01-08, IS_0508_ge_0104 ; решение - max_01-08
CPY max_01-04, max_01-08, !IS_0508_ge_0104 ; решение - max_01-08Исходя из целей данной работы автору было достаточно остановиться на уровне стати́ческой DF-машины и не использовать известные языки потокового программирования. Несмотря на это, некоторые средства автоматизации программирования были разработаны
Важной возможностью является работа с циклами и массивами. Аппаратной поддержкой циклов является именно условный переход к нужной точке программы. Но в DF-машине нет привычного понятия а́дреса! В какую точку программы переходить при достижении некоторого логического условия? Значит, и “goto” бессмысленен… Вот она, “территория счастья” для великого Э́дсгера Ви́бе Де́йкстры!
Для DF-машины привычным методом служит “развёртка циклов” (описание в форме последовательности тела цикла при различных значениях индекса). Для описываемого симулятора автором разработан макрос, позволяющий работать с одномерными “псевдомассивами” (пример ниже):
; пример использования ма́кроса работы с псевдо-массивами
; ПРОГРАММА - вычисление числа PI как суммы
; 4*(1/1-1/3+1/5-1/7+1/9-1/11+1/13-1/15...)
; это (медленно сходящийся) ряд Лейбница
;
SET 1, one ; one←1
SET 2, two ; two←2
SET 4, four ; four← 4
;
SET 0, sum[1] ; начало суммирования элементов ряда
;
for[i]=1,100,1 { ; собственно ма́крос для работы с псевдо-массивами
SET i, m[i] ; m[i]←i (подготовка значений для суммирования)
DRE m[i], two, n[i] ; остаток от деления на 2
MUL n[i], two, k[i] ; умножили на 2
SUB k[i], one, sign[i] ; sign[i]←1/(-1) при i нечётном/чётном
SET 2*i-1, divider[i] ; делитель дроби элемента ряда
;
DIV sign[i], divider[i], series[i] ; готов элемент ряда
;
ADD series[i], sum[i], sum[i+1] ; суммирование членов ряда; 1/4 результата - в sum[101]
}
;
MUL sum[101], four, pi ; результат - число PIСинтаксис макроса такой:
for[I]=I1,I2,I3 {
...инструкция #1
SET I^3, m[I+3] ; присваивание элементу m[I+3] значения I^3
...
...инструкция #N
}где I1,I2,I3 - начальное и конечное значения индекса I и шаг его изменения (константы); в квадратных скобках допускается использование выражений вида X[функция_от_I], где "функция_от_I" может включать 4 основные операции арифметики, получение остатка от деления (%), возведение в степень (^), стандартные функции sin, cos, tg, ctg, arcsin, arccos, arctg, arcctg, sh, ch, th, cth, exp, lg, ln, sqrt, поддерживаются круглые скобки любой вло́женности.
Выражение "функция_от_I" будет вычислено и заменено препроцессором конкретным числовым значением в виде строки. Тело макроса повторяется в соответствие со значениями I1,I2,I3; в случае некорректностей макроса все инструкции комментируются и не окажут воздействия на выполняемую программу.
Внутри тела макроcа возможен вариант инструкции SET с первым операндом в форме "функция_от_I". С помощью такого макроса описывается множество алгоритмов, например, с применением дихотомии (“деление отрезка пополам”).
Анализ протокольных файлов, сгенерированных модулем DF при выполнении программы, позволяет получить варианты расписания выполнения программы при разных параметрах (число АИУ, время обработки каждого оператора, правило обслуживания буфера команд). Также DF-модуль даёт возможность получить файл описания информационного графа для дальнейшего (более глубокого) анализа в системе SPF@home (https://habr.com/ru/post/534722/).
Автор: Валерий Баканов
