
Легко отличить автора гениальной идеи от того, кто её всего лишь понял и пересказал, ведь истинный автор знает предысторию, может показать предшествующие этапы понимания, чувствует границы применимости и особенности.
То же самое со сборкой этой головоломки: миллионы людей умеют делать это по формулам, но сколько из них понимают, что делают? А ведь начать чувствовать кубик Рубика не так сложно!
Но сперва давайте договоримся, зачем нам такая головоломка нужна и чем полезна. Вы же уже слышали шутки про то, что кубик Эрно Рубика – штука многогранная? А видите параллели между кубиком Рубика, шахматами и, например, пианино или гитарой?
Сейчас разберёмся вместе. Но сперва несколько оговорок:
Во-первых, даже если использовать кубик Рубика «неправильно» (например, просто научиться применять какие-то формулы), то далеко не факт, что это плохо. Даже занятия ментальной арифметикой какому-то небольшому проценту детей могут быть полезны, а уж потренировать память и прочую ловкость кистей сборкой кубика почти наверняка не вредно.
Во-вторых, далеко не всем людям, которые в остальных случаях заинтересованы в познании и «расковыривании» мира, именно эта головоломка может дать те самые эндорфины, благодаря которым процесс пойдёт задорно и с удовольствием. Если вам не пошло, то, полагаю, надо просто брать что-то другое, а не пересиливать себя.
И в-третьих, поясню всё же про сходство с пианино и гитарой. Человек, «научившийся» собирать кубик по нескольким формулам, подобен очень начинающему музыканту, освоившему четыре простых аккорда на гитаре или «Собачий вальс» на пианино. Да, уже звучит неплохо и может быть привлекательно для противоположного пола, но всё же это далековато от пользы для развития интеллекта, о которой мы здесь, оказывается, собрались говорить.
Какие же грани пользы даёт нам кубик Кубика?
-
учит быстро принимать решения;
-
тренирует сосредоточенность даже в условиях спешки;
-
развивает память, логику и мелкую моторику пальцев;
-
повышает способность концентрироваться;
-
улучшает скорость реакции;
-
снимает стресс.
Не все из этих пунктов одинаково «прокачиваются» при освоении музыкальных инструментов, но в музыке есть много другого хорошего, так что не будем спорить, что лучше, а перейдём к делу – начнём чувствовать и понимать кубик. Перечислю три ветки «прокачки», прекрасно помня, что есть и другие хорошие подходы, а также совершенно не настаивая на необходимости доходить до любого из перечисленных ниже методов быстрой сборки:
-
Собрать одну грань, не обращая внимания на другие -> Собрать одну грань, согласовав её с центрами четырёх соседних граней -> Аналитический F2L для завершения сборки первых двух слоёв -> Аналитическая сборка третьего слоя -> … -> вероятен переход к методу CFOP (Fridrich).
-
Расставить правильно все 8 углов (т.е. решить кубик 2х2х2) -> Добавить к ним 4 рёберных кубика из любой центральной грани -> Расставить оставшиеся 8 рёберных кубиков -> Расставить центры -> … -> возможен переход к методу ROUX.
-
Собрать правильно блок 2х2х2 (т.е. выбрать один угол и правильно расположить рядом с ним его соседей) -> Расширить его до блока 2х2х3 -> … -> вероятен переход к методу PETRUS.
-
...
Сейчас мы перейдём к деталям, но сперва обращу ваше внимание на то, что обычно хорошим является тот способ исследования кубика, который нравится обучающемуся. Другими словами, рассуждения вида «многие рекорды поставлены методом Джессики Фридрих, поэтому пойду по первому пути» могут помешать, так как тут важнее сконцентрироваться на предпочтениях своего . Наша цель – сперва начать лучше чувствовать кубик, а уже потом решать, хочется ли вообще собирать его быстро.
Иногда бывает удобно, если рядом есть источник собранных кубиков, поскольку это даёт возможность легче проводить эксперименты. Если умеющий восстанавливать кубики человек найдёт время, чтобы поддержать исследовательский порыв обучающегося, то будет здорово. Но даже и без этого всё работает хорошо.
Играем с кубиком
Всё, хватит текста, наконец-то переходим к картинкам. Предлагаю смотреть на кубик сверху большим глазом. Так нам всегда видно пять граней, что очень удобно.
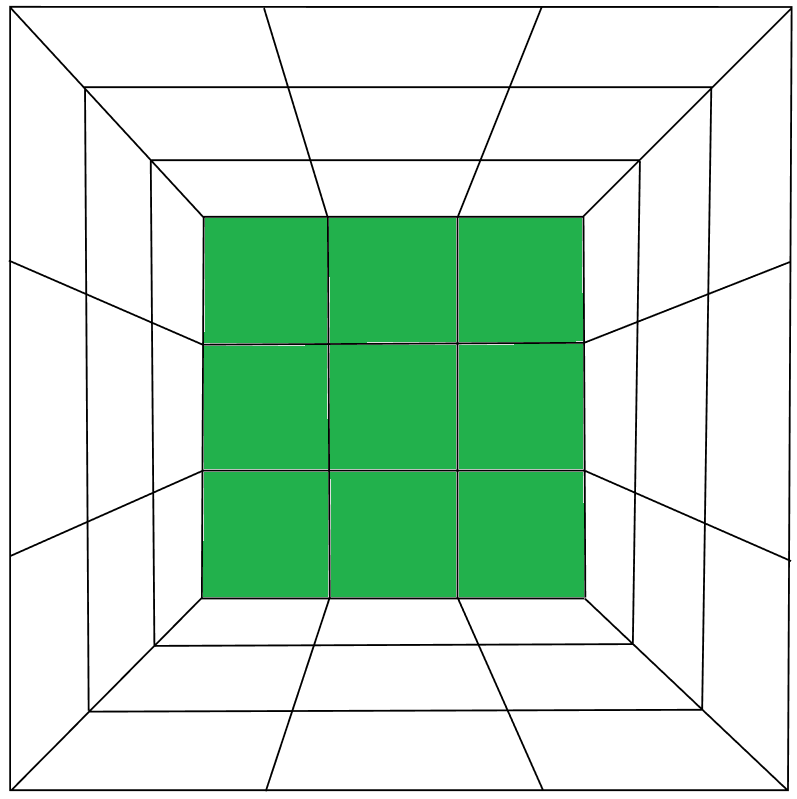
На этой картинке показано, как можно обозначить сборку одной грани. Здесь зелёным отмечены более-менее правильно стоящие элементы, а белым те, которые пока можно игнорировать. Многие начинают знакомиться с кубиком именно с этого, замечали? Кто-то может воскликнуть, что это глупо и неправильно, но я не соглашусь: если мы хотим понять кубик, то даже такое упражнение имеет смысл. А тем, кто интересуется путными подходами к обучению, могу ещё порекомендовать книги Жени Кац (у неё для детей прекрасные рабочие тетради, но и для учителей/родителей тоже всё отлично).
Пройдя этот этап, исследователь может внезапно обнаружить шесть центральных элементов, которые друг относительно друга перемещаться не могут. А это означает, что надо не их согласовать с собранной гранью, а наоборот – научиться собирать первую грань, согласуя её с центрами. Немного повозившись, мы приходим к следующему прорыву:
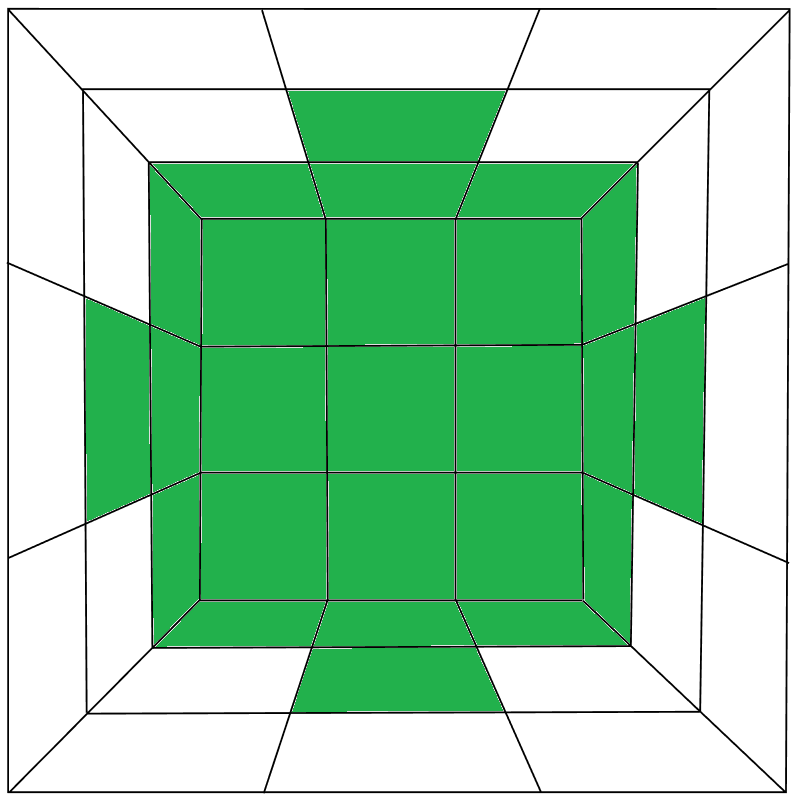
Да, у нас наконец-то полноценно собран первый слой, причём он согласуется с центральными элементами второго слоя (можно даже сказать, что половина второго слоя тоже собрана). Осталось совсем чуть-чуть, да? И вот тут многим начинают мешать раньше времени поставленные угловые элементы, ведь придумать способ собрать второй слой кубика Рубика с ними оказывается сложнее, чем без них.
Шаг назад, два вперёд
Да, это то, что я предлагаю сделать – откатиться назад. Сейчас нам нужен только собранный «согласованный крест». Опытные люди уже давно хотели это предложить, верно?
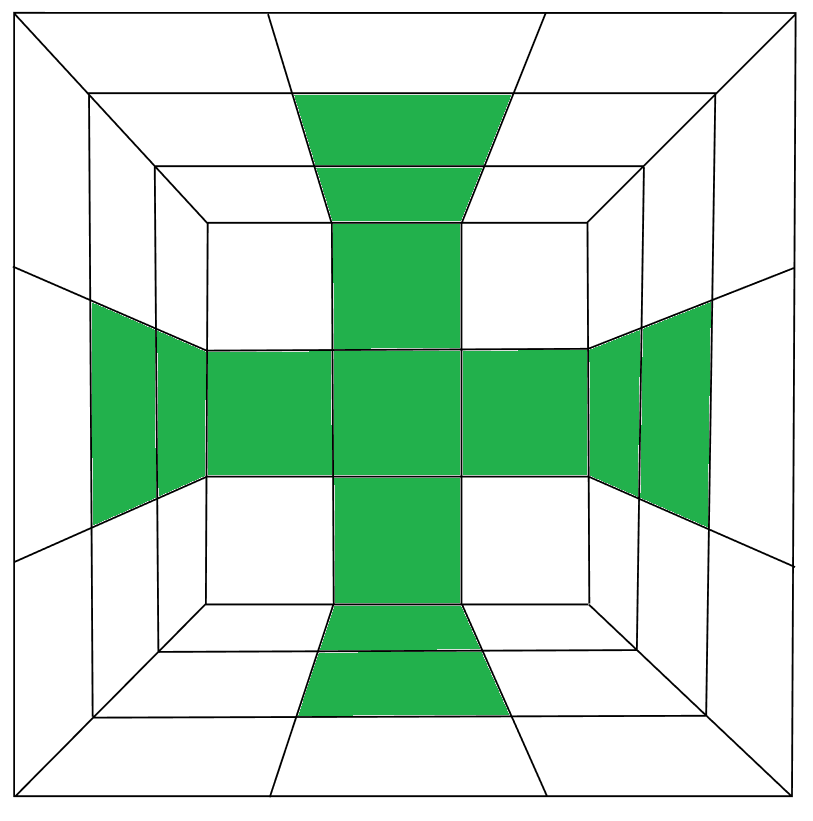
Удаление уголков выглядит странно? Возможно, да. Но это не более странно, чем одновременно смотреть на пять граней кубика гигантским глазом, а ведь именно этим мы занимаемся. Ничего, сейчас я всё объясню. Оказывается, если мы не будем дорожить уголками (а зелёным цветом мы отмечаем не столько то, что собрано, сколько то, что нам жалко разломать), то сможем собирать целые столбики из двух элементов (углового и рёберного). И потом мы эту пару сможем поставить сразу на правильное место, перейдя в следующее радостное состояние (опытные люди его ещё называют XCross):
Тут может возникнуть резонный вопрос, а зачем тогда был нужен предыдущий этап (сборка одной грани), если теперь нам достаточно только одного креста без углов?
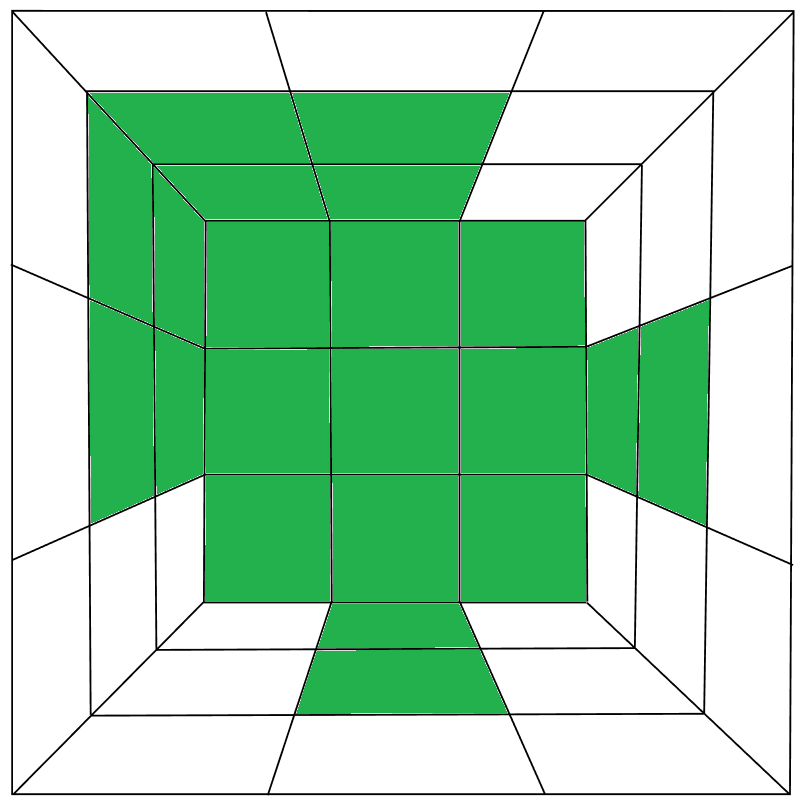
Ответ может быть следующим: стремясь собрать целую грань, мы многое поняли про устройство кубика, поэтому теперь чувствуем его лучше. Сейчас нам надо собирать и ставить на место целые пары из углового и рёберного кубика, что предполагает умение ставить угол на место. А ведь именно это умение мы развили, пока учились собирать первую грань. Кстати, потом мы начнём так хорошо чувствовать кубик, что будем собирать «крест» не более, чем за 8 движений. А кто-то потом и XCross станет собирать «сразу».
Как же нащупать этот способ аналитически собрать пару? Тут нужно время и терпение. Мастера запомнили десятки формул для разных начальных расположений элементов пары, но мы-то пока хотим каждую пару собирать «методом пристального взгляда». И это вполне возможно, хоть и потребует усилий.
Если будет совсем тяжело, то имеет смысл по запросам вида «F2L для новичков» подсмотреть идеи, но я бы рекомендовал ограничиваться одной «первой мыслью» из обучающих видео, а не впитывать всю методику сразу (дайте обучающемуся как можно больше шансов «придумать самому», потому что это существенно для глубины понимания). Также ниже есть годное видео про первые шаги в F2L (first-two-layers).
Аналогичным образом удастся поставить и три оставшиеся пары, после чего обычно начинается кризис: как только собраны первые два слоя, их очень жалко ломать. Значит, нужно придумать способ собрать третий слой, не испортив первые два. Как же это сделать?
Это чуть сложнее, чем научиться нащупывать пары и собирать их в столбики на предыдущем этапе. Благо, есть несколько подходов к сборке третьего слоя. Я бы рекомендовал выделить как минимум пять-семь часов чистого времени на самостоятельный поиск решений. Если терпение кончится, то рекомендую второе и третье видео ниже.
От углов к центру
А иногда хочется собирать кубик, не начиная с одной какой-то грани, а расставив сперва все углы. Нередко с этого начинают люди, у которых кроме кубика 3х3х3 есть и другой полезный тренажёр – кубик 2х2х2.
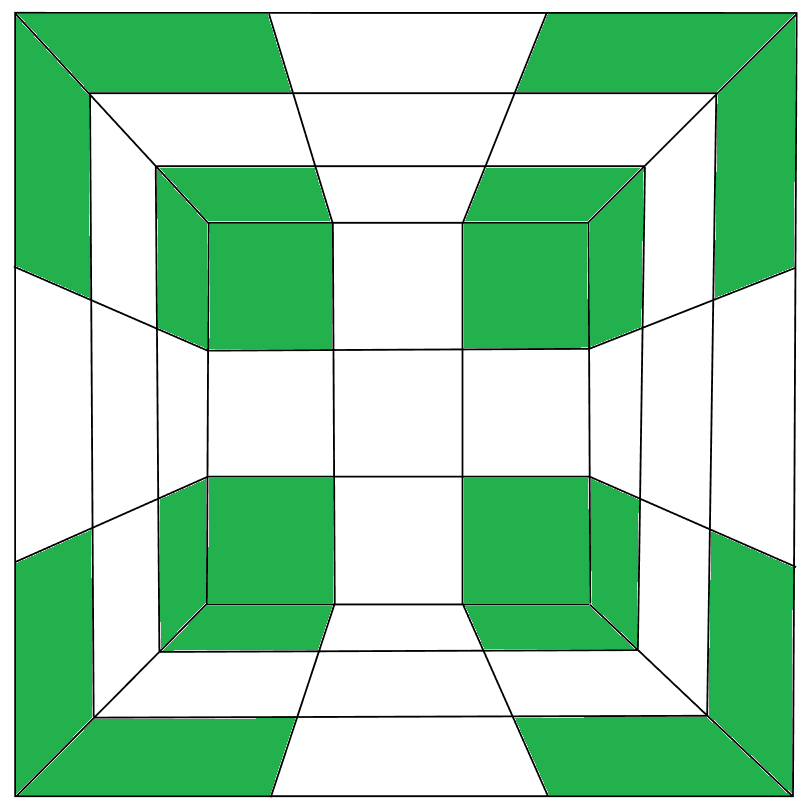
После этого можно идти разными путями, но один из самых популярных – сборка четырёх столбиков (т.е. между восемью углами добавляем четыре рёберных кубика, чтобы получить четыре столба). Делать это можно самыми разными способами, формулы не нужны, а ощущение «на кончиках пальцев» возникает.
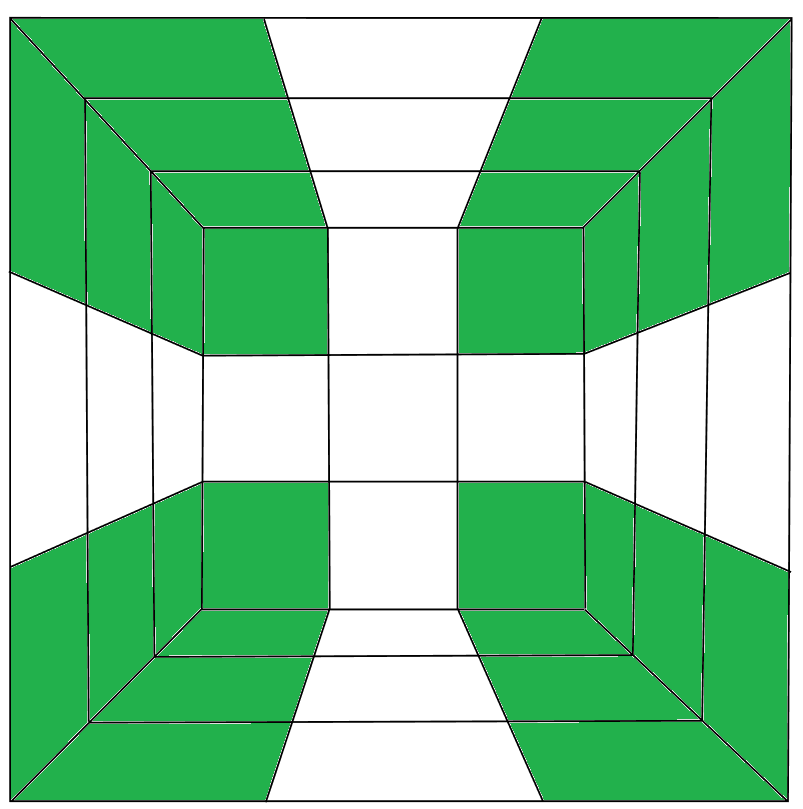
Ну а дальше почти столь же естественно расставляются оставшиеся восемь рёберных кубиков, после чего придумать перестановку центральных элементов совсем легко. Если на этом пути будут сложности, то по запросу про «Метод Морозова» должны найтись идеи. Ниже вы можете найти видео с пояснениями.
Зачем всё это?
Выше я старался не давать конкретных формул или методов, а стремился показать способы «покачать» свою способность понимать кубик Рубика. Не собирать, а именно понимать. Ведь брать производную функции может почти любой путёвый первоклассник (там же простейшие преобразования строк – можно быстро научить), но не каждый второкурсник понимает, «что конкретно он только что взял».
Так и здесь: подходы выше направлены на то, чтобы начать чувствовать кубик, а только потом думать про быструю/эффективную/... сборку кубика. Кстати, знаете, чем они отличаются?
Напомню, что есть разные дисциплины:
-
Сборка кубика на скорость (с вариациями «двумя руками», «одной рукой», «ногами», «сборка трёх кубиков при жонглировании ими же», ...),
-
Сборка кубика на количество действий (очень интересная дисциплина про понимание; как и в шахматных турнирах, есть сложности из-за попыток применять компьютер),
-
Сборка кубика вслепую (с суровой вариацией «мультиблайнд», в которой мы сперва запоминаем много кубиков, а потом последовательно собираем их, не убирая повязку).
Другими словами, развивать себя даже в контексте кубика Рубика можно в самые разные стороны. А раз так, то выбор этот лучше делать осознанно, чувствуя нюансы снаряда, а не просто так выучивать первые попавшиеся формулы из первого попавшегося видеоролика. Короче, всё как с музыкальными инструментами и теми же шахматами.
Мне в своё время было интересно научиться собирать кубики произвольного размера с открытыми и закрытыми глазами, а вот поиск кратчайшего решения пока не даётся. Могу поделиться неплохим побочным эффектом: дети повторяют за родителями, поэтому тоже осваивают кубики, что скорее хорошо, чем плохо (конечно, главное – не давить, чтобы не вызвать отвращение к любым самостоятельным исследованиям и математике вообще).
Ссылки
Обучающие видео
Выше я обещал четыре полезных ролика:
1) Здесь аккуратно рассказано, как заполнить «столбиками» первые два слоя.
2) Тут автор делится подходами к третьему слою:
3) Этот ролик на английском языке можно было бы ставить первым и единственным. Он близок по духу к предыдущему, но более универсальный и ближе к математике:
4) Про метод Морозова и развитие интуиции есть здесь:
Всё же ещё раз усомнюсь в полезности просмотра всех этих роликов до самостоятельных экспериментов. По-моему, надо сперва много пробовать, а потом чуть-чуть смотреть подобные видео до первого же осознания «Ого, и так можно, оказывается!», после чего сразу выключать ролик и возвращаться к экспериментам.
А как вы осваивали головоломки? Какие считаете самыми полезными? Какие не любите?
Автор: Ilya Lichman





