Сегодня мы рассмотрим алгоритм TILT (Transform Invariant Low-rank Texture) и множество его методов применения в области Computer Vision. Статья будет нести несколько обзорный характер, без плотного углубления в математические дебри.
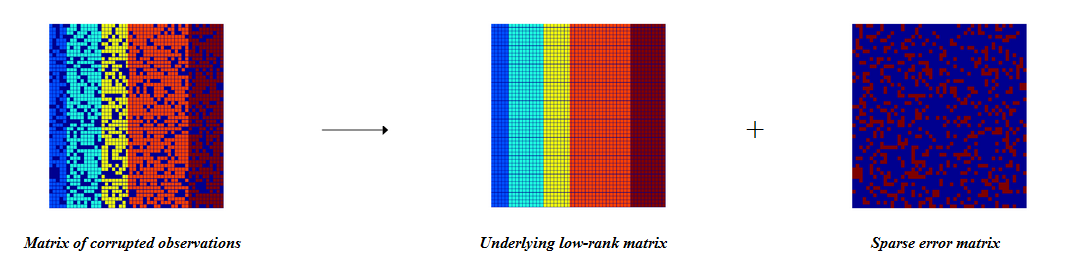
Идея алгоритма, можно сказать, произрастает из конкурса Netflix Prize, который, по сути, является задачей коллаборативной фильтрации, где мы имеем матрицу пользователей и их оценок: матрица разреженная, в ней отсутствуют элементы, а так же может присутствовать шум, а нам надо для каждого фильма предугадать, какую оценку ему поставит каждый пользователь, т.е. мы заполняем матрицу.
Изображение это тоже матрица!
Мы будем использовать определение ранга матрицы
Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
И какое же изображение будет иметь низкий ранг? Например изображение где есть регулярные структуры:

Как показано на картинке сверху поста, мы моделируем нашу исходную матрицу как матрицу низкого ранга (low rank) + разреженную матрицу с шумом, т.е. на деле это может выглядеть как-то так:

Теперь про сам алгоритм TILT:
К изначальной постановке задачи мы добавляем искажение, т.е. мы восстанавливаем не только матрицу низкого ранга и матрицу с шумом, но и геометрическое искажение(например поворот, аффинное преобразование, проективное преобразование) при котором минимизируется ранг матрицы.
Мы будем задавать наше преобразование матрицей гомографии, хотя возможно задать и более сложное преобразование.
Но на практике не минимизруют ранг матрицы напрямую, а берут nuclear norm, причем для матрицы с шумом берется L1 norm, как я понимаю это делается для регуляризации, т.е. чтобы матрица была разреженной.
Постановка задачи минимизации:
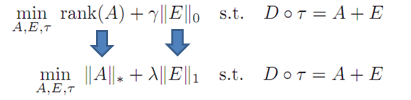
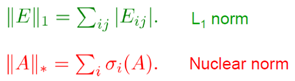
Затем алгоритм итеративно сходиться к оптимальному решению, используя методы оптимизации, как показано на видео:
Теперь переходим к самому интересному, а именно к практическим применениям:
Автокалибровка искажения линз:

Дополненная реальность:

Автоповорот текста, вывесок и штрихкодов:


И да, низкий ранг имеют не только картинки с повторяющейся структурой, но и симметрия снижает ранг! Еще стоит заметить, что если у человека повязка на одном глазу(человек-пират) или на одну сторону зачёсана челка, это не помешает алгоритму «найти симметрию» ведь мы помним что алгоритм моделирует так же и шум.
Автоповорот лиц, козлов и любых предметов имеющих симметрию:

Автоповорот автомобильного номера(небольшой привет недавним постам про распознавание автомобильного номера от ZlodeiBaal изображения взяты отсюда):
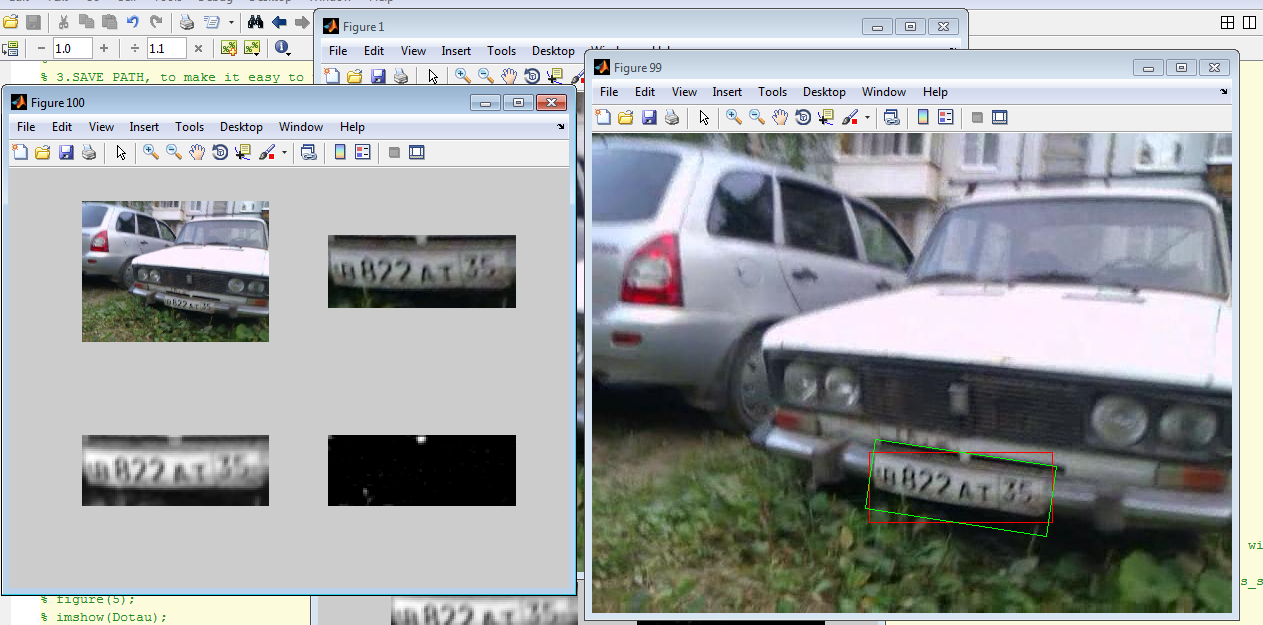
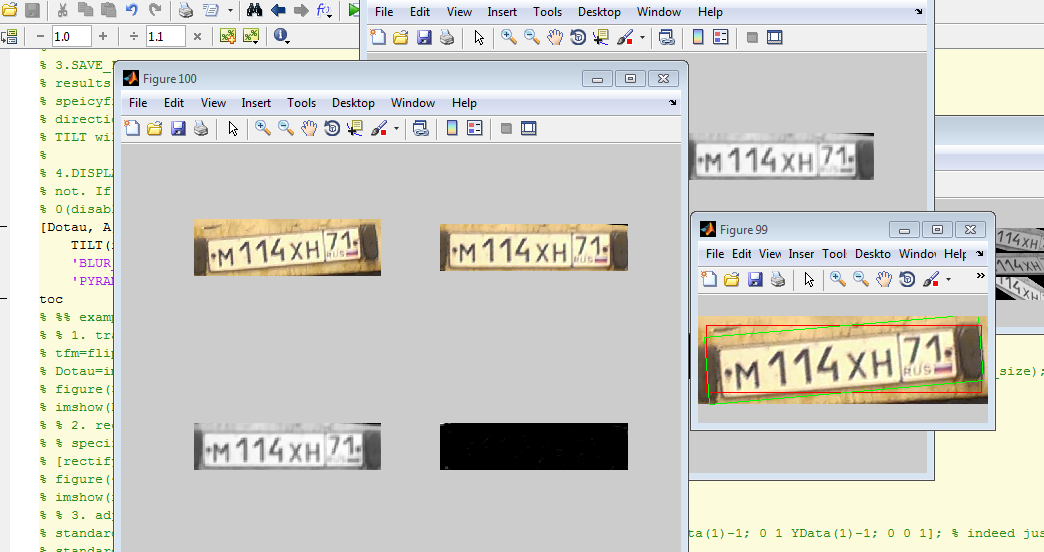
А что, алгоритм и правда такой хороший?
Не совсем. Сходимость алгоритма к правильному решению зависит от инициализации, вот пара негативных примеров:

Что дальше?
Вот ссылка на код на Matlab: TILT code
Ссылки на публикации: TILT: Transform Invariant Low-rank Textures
Ссылки на лекции: Low-rank modeling | The Pursuit of Low-dimensional Structures in High-dimensional Data, Yi Ma, Microsoft
Автор: mrgloom






