Взгляд компьютерным зрением на работу коммунальных служб

Стоит признать, мы таки живем в эпоху киберпанка. Он не похож (пока) на мрачные миры Ридли Скотта и братьев Вачовски, но вполне отвечает меткому определению: high tech, low life. К третьему десятилетию двадцать первого века российская провинция так и не научилась содержать пешеходную инфраструктуру в достойном состоянии, но плотно обвешалась уличными веб‑камерами, круглосуточно взирающими на пробирающихся по заснеженным тропинкам пешеходов.

Небольшое исследование сети подсказывает, что системы аналитики качества уборки дорог и тротуаров зимой на основе данных камер уже внедрено, например, в Москве и Казани. Но то ли это тайна реализации, то ли на самом деле оно так и есть, озвучено отслеживание именно уборочной техники, а главная метрика — счастье пешехода, осталась без внимания. Хотя делается это именно для пешеходов, и параметры их движения (скорость, направление и т. д.), кажется, должны полностью характеризовать качество работы служб ЖКХ.

Проберемся к истине сквозь сугробы видео анализа. Откроем карту города, выберем несколько камер, выгрузим видеопоток, полученный в одинаковое время в будние дни. Сделаем это при разных погодных условиях: после снегопада, в гололедицу и при небольшой плюсовой температуре.

Шаг первый: детектируем пешеходов

Чтобы не быть голословным, сразу статья: Object Detection in 2023: The Definitive Guide. Тема очень популярная, написано по ней немало. Подходы делятся на два периода. Первый — традиционный, главное из него: детектор Виолы — Джонса (2001), детектор на основе гистограммы направленных градиентов (2006), а также детектор на основе модели деформируемых деталей (2008). После 2014 года безоговорочную власть в этой области захватили алгоритмы на основе свёрточных нейронных сетей. Среди последних выигрывает YOLO, он точен и достаточно быстр (есть шустрая tiny‑версия, немного жертвующая точностью).

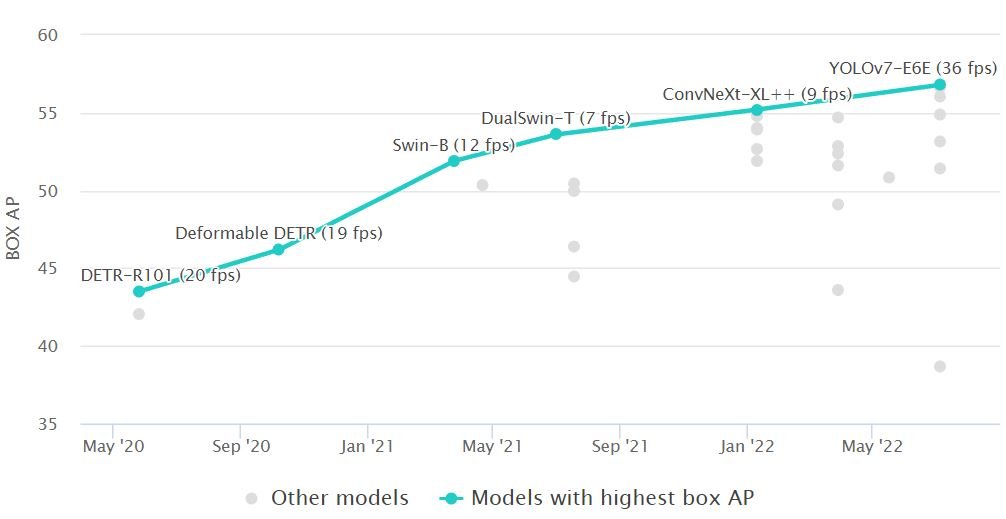
Не долго думая, решаем в сторону YOLO. Он живет на GitHub, где можно скачать веса предобученных моделей. В нашей задаче вполне достаточно tiny‑версии, по причине, которую озвучу позже.

Шаг второй: отслеживаем пешеходов

Итак, пешеходов на видео нашли. Но этого не достаточно, чтобы отследить их передвижение — пока что все детектированные объекты на видео — один и тот же квантовый пешеход. С задачей трекинга в связке с YOLO отлично справляется алгоритм DeepSort. Связывание строится на основе внешних признаков объектов и их динамики движения. Есть статья на Хабре, есть готовый код на GitHub.

Отлично, теперь мы знаем о перемещениях пешеходов по изображению. Можем измерить пиксели за кадр. Чего, конечно, делать не будем, а проследуем в реальный мир с метрами и секундами.

Шаг третий: исправляем дисторсию

Если приглядеться к имеющимся «пикселям за кадр», видно, что ближе к краю изображения пешеходы двигаются медленнее. В реальности это, естественно, не так — объектив камеры деформирует изображение по типу «бочка», сжимая объекты на периферии кадра. В идеальном мире, каждая камера калибруется отдельно и дисторсия компенсируется на основе полученных данных. В реальности, зная модель камеры, можно найти в сети ее коэффициенты дисторсии и довольствоваться этим.

import numpy as np
import cv2

# исходное изображение
src = cv2.imread("frame.jpg")
width  = src.shape[1]
height = src.shape[0]

# коэффициенты дисторсии
distCoeff = np.zeros((4, 1),np.float64)

# уникальны для конкретной модели
k1 = -1.0e-5;
k2 = 0.0;
p1 = 0.0;
p2 = 0.0;

distCoeff[0,0] = k1;
distCoeff[1,0] = k2;
distCoeff[2,0] = p1;
distCoeff[3,0] = p2;

# внутренняя матрица камеры
cam = np.eye(3, dtype=np.float32)

cam[0,2] = width/2.0  # центр по x
cam[1,2] = height/2.0 # центр по y
cam[0,0] = 10.        # фокусное расстояние по x
cam[1,1] = 10.        # фокусное расстояние по y

# исправленное изображение
dst = cv2.undistort(src, cam, distCoeff)

Интересный момент. Зная, что пешеходы, при достаточном количестве накопленных данных, должны двигаться с одинаковой средней скоростью по всей площади кадра (при условии схожих условий), можно, измеряя их скорость, калибровать камеры. Задача преобразования изображений сводится в этом случае к выравниванию средней скорости по всей площади кадра.

Шаг четвертый: проецируем землю

Тот прямоугольник поверхности земли, который мы видим в кадре в реальности имеет очертания вытянутой трапеции. Перевести координаты пешеходов в плоскость земной поверхности призвана перспективная проекция.

Преобразование выполняется путем умножения на трехмерную матрицу проекции, коэффициенты которой можно получить, взяв несколько точек из кадра и задав соответствующие им точки в плоскости проекции. Я для этого взял два объекта: один на переднем, другой на заднем плане, имеющие одинаковый в действительности размер.

import cv2
import numpy as np

points_from = [[15, 225], ...] # исходные точки
points_to = [[960, 225], ...] # точки после преобразования

src = np.float32(points_from)
dst = np.float32(points_to)

M = cv2.getPerspectiveTransform(src, dst) # прямая матрица трансформации
Minv = cv2.getPerspectiveTransform(dst, src) # обратная матрица трансформации

Перемножая координаты в плоскости кадра на полученную матрицу мы переводим их в координаты земной поверхности. Наглядно это можно увидеть, подействовав матрицей на изображение с помощью функции OpenCV warpPerspective. При этом получается следующее изображение, примерно отвечающее виду сверху на рассматриваемую сцену:

Проекция импровизированной координатной сетки с помощью обратной матрицы трансформации в плоскость кадра дает следующий результат:

Шаг пятый: вычисляем скорость

Теперь все готово — массив точек, полученный на выходе алгоритма трекинга, мы подвергаем двум последовательным преобразованиям, сначала исправляя дисторсию, а затем выполняя перспективную проекцию. Эти координаты можно использовать для анализа движения пешеходов.

Для каждой из полученных координат мы сохранили соответствующий порядковый номер кадра. Это спасает нас в ситуации, когда детектор пропускал цель один или несколько кадров подряд. Этим грешит tiny‑версия YOLO. Но пешеходы, как правило, движутся прямолинейно, и сохраненный номер кадра позволяет вычислить скорость даже с пропущенным в процессе движения координатами.

PX_PER_METER = 235 # пикселей на метр в проекции
FRAMES_PER_SECOND = 14.4 # частота кадров в видео

distance = 6 # на сколько пикселей сместился пешеход между кадрами
frames_passed = 2 # сколько кадров сменилось между последовательными детектированиями

speed = (distance / frames_passed) * (FRAMES_PER_SECOND / PX_PER_METER)    

Для перевода полученного значения скорости в км/ч его необходимо домножить на 3.6 дополнительно.

Шаг шестой: считаем метрики

В голову пришли две метрики, отражающие насколько быстро движутся пешеходы и насколько скученно пролегают траектории их движения.

1. Средняя скорость пешеходов.

2. Суммарная площадь траекторий.

Здесь ничего экстраординарного — скорость усредняем по медиане, нивелируя выбросы вроде стоящих на одном месте людей и ошибок трекинга, площадь считаем, суммируя координаты с движением.

Шаг седьмой: рисуем картинки и графики

Переходим к тепловым картам и графикам. Как уже было указано выше, были выбраны три типа погодных условий:

• после снегопада (тротуары не расчищены);

• гололедица (тротуары не обработаны);

• небольшая плюсовая температура.

Последнее в списке состояние считаем базовым, когда ничего не затрудняет движение пешеходов. Нанесенное на координатную сетку, оно выглядит так (цвет кодирует среднюю скорость движения, яркость — плотность движения в этой области).

Далее смотрим на движение в гололедицу и замечаем как заметно падает скорость и плотность передвижения пешеходов.

Теперь попробуем другой печальный вариант — не убранный после сильного снегопада снег. Пешеходы в этом случае придерживаются тропинок, что, впрочем, не сильно сказывается на скорости.

Посмотрим на числовые значения скорости и площади. Скорость в километрах в час, площадь в «попугаях» — координатах импровизированной координатной сетки.

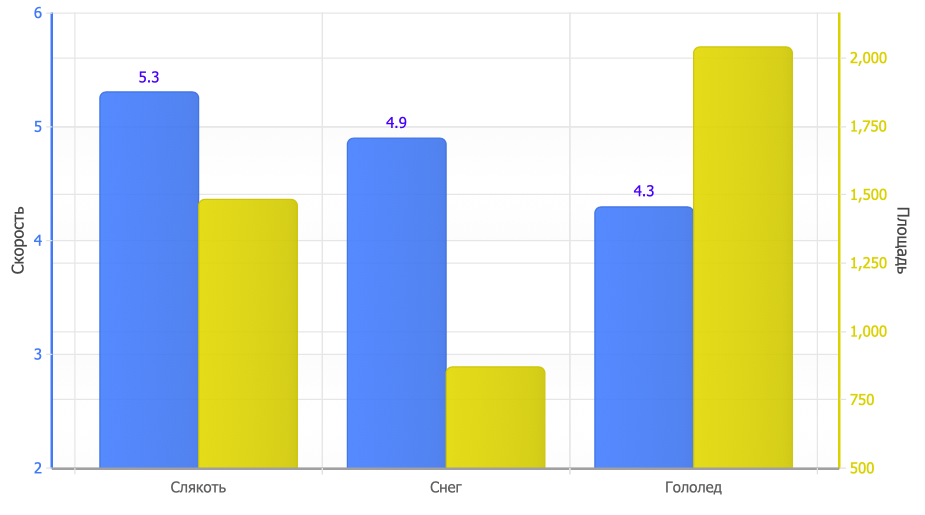
Ничего сверхъестественного, но забавно. В гололед мы передвигаемся медленнее всего. По снежным тропинкам быстрее, хотя и не сильно. Но двигаемся при этом очень скученно вдоль протоптанных направлений. В гололед же разбредаемся максимально широко, минуя встречных прохожих и в поисках лучшего сцепления.

Итого

Небольшое упражнение на несколько вечеров показывает, что анализируя видео с городских уличных камер, можно на основе нескольких метрик оценить насколько качественно справляются со своей работой службы ЖКХ. Где не убран снег, а где не обработан лед. Потенциально эта оценка отражает именно то, для чего и производится уборка — комфорт передвижения пешеходов.

Позднее будет интересно сравнить эти данные с летними, от которых можно будет оттолкнуться как от эталонных. Кроме того, вероятно, достаточно много данных содержит сама форма траектории движения, так как визуально она сильнее отклоняется от прямолинейной в гололед. Подобная метрика также может говорить о качестве содержания пешеходной инфраструктуры.