Привет! Мы вдруг поняли, что наша последняя статья про Эльбрус вышла год назад. Поэтому мы решили исправить эту досадную оплошность, ведь мы не бросили эту тему!
Сложно представить распознавание без нейронных сетей, поэтому мы расскажем о том, как мы запустили 8-битные сетки на Эльбрусе и что из этого получилось. Вообще, модель с 8-битными коэффициентами и входами и 32-битными промежуточными вычислениями крайне популярна. Например, Google [1] и Facebook [2] завели ее собственные реализации, которые оптимизируют доступ в память, задействуют SIMD и позволяют ускорить вычисления на 25% и больше без заметного снижения точности (это конечно зависит от архитектуры нейронной сети и вычислителя, но нужно же было объяснить, насколько это круто?).
Идея замены вещественных чисел на целые для ускорения вычислений витает в воздухе:
- На специализированных платах и ПЛИС часто просто нет блоков вещественных операций и при запуске сеток на них все равно приходилось использовать форматы с фиксированной точкой. Разумеется, хочется делать это более “умным” образом, чем просто взять обученную во float сетку и заменить тип данных, поскольку так мы не можем контролировать точность результирующей сети;
- При вычислениях на центральном процессоре. Где-то в коллективном бессознательном у программистов хранятся воспоминания о том, что вещественные вычисления выполняет сопроцессор, который… так скажем, не очень быстрый. В современных процессорах различия в десятки раз в скорости одной операции уже нет, но зато есть векторные расширения (SIMD). И c помощью 128-битного SIMD можно обработать 4 float’а и 16 uint8. Вот и различие в 4 раза, что вовсе немало;
- Во многих вычислительных задачах доступ к данным в памяти занимает время, сравнимое со временем вычислений. Меньше объем данных — быстрее их загрузка!
И 8-битная нейросетевая модель [3] позволяет удовлетворить этот запрос. Она крайне полезна при работе со специализированными, встраиваемыми и мобильными устройствами, когда нет видеокарты или не хочется ее использовать.
Рассматриваемая модель оперирует 8-битными целыми беззнаковыми коэффициентами, которые перед умножением преобразуются в 16-битные, то же самое происходит со входными сигналами. Для суммирования используется 32-битный аккумулятор. Перед вызовом следующего слоя выполняется нормировка, чтобы снова получить беззнаковые 8-битные значения. Таким образом, переполнения при вычислениях исключены и полученная сумма произведений является верной при любых входных данных.
Самое основное, что нужно сделать для реализации такой модели — это реализовать сверточные слои. Сверточный слой состоит из собственно свертки (см. Рис. 1) и нелинейной функции активации:
где 



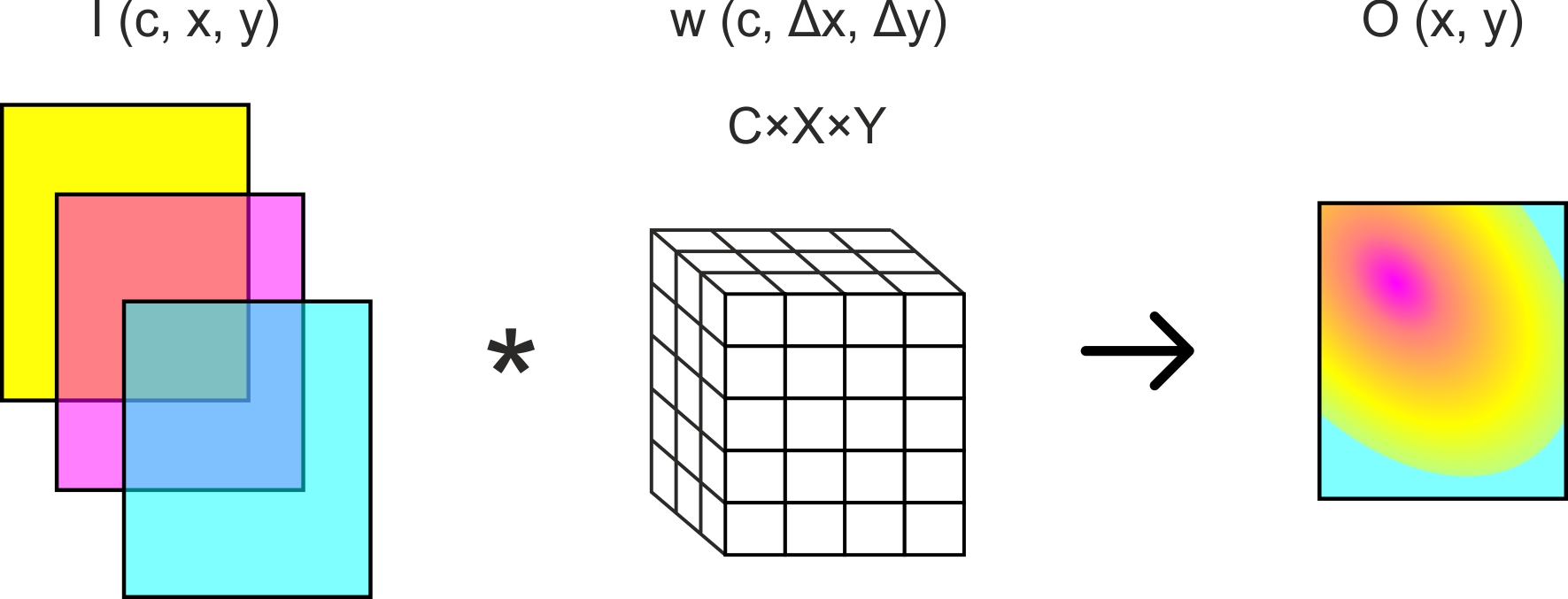
Рис. 1. Свертка многоканального изображения с одним фильтром размера C x X x Y.
Вычислительно эффективная реализация свертки для центральных процессоров — это реализация в виде одной операции умножения матрицы на матрицу [4]. В ней предлагается представить сверточные фильтры в виде одной матрицы, в которой каждой строке соответствует один фильтр, все коэффициенты которого выписаны последовательно. На основе входного изображения формируется матрица, в которой одному столбцу соответствует одно "приложение" фильтра — т.е. коэффициенты входного изображения, на которые умножаются коэффициенты фильтра. Число столбцов соответствует числу выходов одного сверточного фильтра, т.е. числу слагаемых в сумме (1). При этом чаще всего используется "перемежающийся" порядок перечисления элементов, т.е. последовательно расположены первый элемент первого канала фильтра (или изображения), первый элемент второго канала фильтра и т.д.
Поэтому нашей основной задачей была оптимальная реализация матричного умножения для 8-битных матриц с 32-битными результатом.
Архитектура Эльбрус
Все-таки Эльбрусы пока не стоят в каждом офисе, поэтому немного напомним, что же это за архитектура.
Эльбрус – микропроцессорная архитектура, построенная по принципу широкого командного слова. Это означает, что процессор Эльбрус способен исполнять за один такт несколько элементарных команд, которые вместе образуют одну большую инструкция — широкое командное слово. Их формирование происходит полностью на этапе компиляции программы оптимизирующим компилятором. Он способен выполнить глубокий анализ исходного кода и планирование команд по вычислительным устройствам эффективнее, чем аппаратные планировщики команд, так как на этапе компиляции доступно значительно больше как временных, так и вычислительных ресурсов [5-7].
Архитектурно это реализовано с помощью 6 наборов вычислительных устройств на каждом ядре процессора (каждый со своим конвейером операций), которые мы будем называть вычислительными каналами. Эти каналы не идентичны: каждый содержит арифметико-логические устройства, поддерживающее лишь некоторые из доступных операций. Так, например, сложение целых чисел поддерживается всеми каналами, в то время как большая часть векторных операций, выполняемых над упакованными в широкие регистры числами, доступны только на двух каналах. Это означает, что использование векторных операций не всегда оправдано в плане производительности.
С развитием архитектуры Эльбрус АЛУ для каждого вычислительного канала претерпевали некоторые изменения. Информация по основным вычислительным операциям приведена в Таблице 1 для различных версий системы команд (СК). Длина машинного слова предполагается равной 32 бита.
Таблица 1. Параметры АЛУ в зависимости от версии системы команд. В таблице через "/" приводится информация о числе каналов, поддерживающих операцию, и длительность в тактах.
| Процессоры | Эльбрус-4С | Эльбрус-8С, Эльбрус-1С+ | Эльбрус-8СВ |
|---|---|---|---|
| Ширина векторного регистра, бит | 64 | 64 | 128 |
| Целочисленное сложение (64 бита) | 6/1 | 6/1 | 6/1 |
| Вещественное сложение (64 бита) | 4/4 | 6/4 | 6/4 |
| Широкое целочисленное умножение (32х32 -> 64 бита) | 4/4 | 4/4 | 4/4 |
| Вещественное умножение со сложением (64 бита) | 4/8 | 6/8 | 6/8 |
| Целочисленное сложение (вектор) | 2/1 | 2/1 | 2/1 |
| Целочисленное умножение с попарным сложением (вектор) | 2/2 | 2/2 | 2/2 |
| Перестановка байтов (64 бита) | 4/1 | 4/1 | 4/1 |
| Распаковка данных (вектор) | 2/1 | 2/1 | 2/1 |
| Подкачка данных APB | 4/5 | 4/5 | 4/5 |
Кроме того, в архитектуре Эльбрус предусмотрена аппаратная поддержка быстрого доступа в память в виде иерархической системы кэш-памяти и устройства предварительной подкачки массивов APB (array prefetch buffer). APB обеспечивает быструю загрузку n-линейных массивов, хранящихся в основной памяти вычислителя. В отличие от кэш-памяти, нацеленной на предподкачку часто используемых данных, APB оптимизирует время доступа к массивам, использующимся небольшое число раз и обрабатывающимся преимущественно последовательно. Применение APB имеет некоторые ограничения:
- его можно использовать при отсутствии вызовов функций в процессе его непосредственного использования;
- в СК версий 3 и 4 APB можно использовать только при работе с выровненными данными, в СК версии 5 это требование ослаблено и будет полностью снято в СК версии~6.
При этом следует понимать, что APB будет эффективен:
- при достаточно большом числе итераций цикла, в котором происходит обращение к APB;
- при доступе к элементам массива, отстоящим друг от друга не более чем на 32b;
- при отсутствии конфликтов по памяти с операциями записи между итерациями, либо при достаточно большой дистанции таких зависимостей.
Подходы к эффективному умножению матриц на архитектуре Эльбрус
Для вычислительно эффективной реализации матричного умножения необходимо обеспечить максимальную загрузку вычислителей процессора, а также загрузку необходимых данных из памяти перед вычислениями, так как это время способно на порядок превышать время выполнения элементарных арифметических операций. Отличительной особенностью матричного умножения является тот факт, что один и тот же элемент матрицы может использоваться для вычисления нескольких элементов результата. Поэтому в статье Goto [8] предложен метод загрузки элементов матриц в зависимости от их размеров и параметров подсистемы памяти вычислителя. Основная идея заключается в том, чтобы обрабатывать матрицы блоками, причем размеры блоков выбираются таким образом, чтобы блоки помещались в кэш первого и второго уровня соответственно. Это позволяет обеспечить быстрый доступ к элементам матриц и использовать их многократно для вычисления вклада этих элементов в целый блок результата.
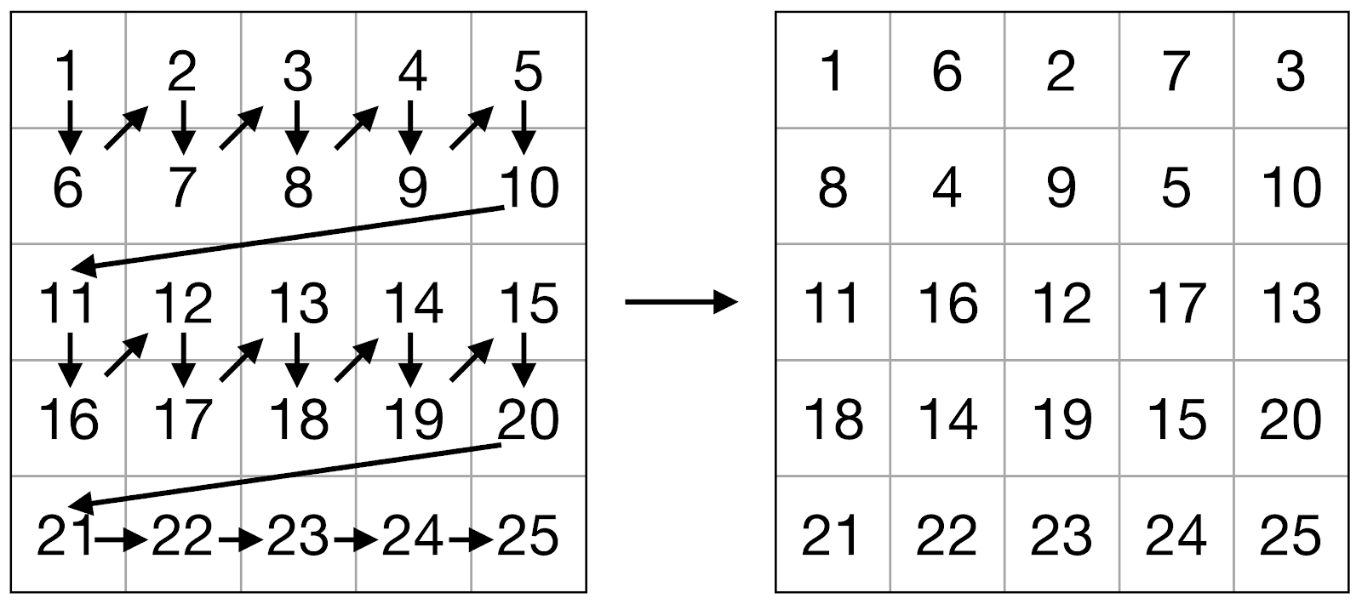
Мы использовали этот алгоритм, с тем лишь отличием, что внутри блока матрицы элементы подверглись операции упаковки (см. Рис. 2-3). Задача операции упаковки — обеспечить оптимальный порядок элементов для их последующей загрузки в регистры и использования векторных команд. Упаковку необходимо выполнить всего один раз для каждого блока, т.е. ее сложность линейно зависит от числа элементов матрицы. Кроме того, упаковка позволила решить проблему с невозможностью использовать APB из-за произвольного выравнивания адресов элементов матриц: было выполнено дополнение нулевыми элементами до ближайшего размера, кратного 8 (для 64-битных регистров) для операндов умножения и до размера кратного 2 для результата.
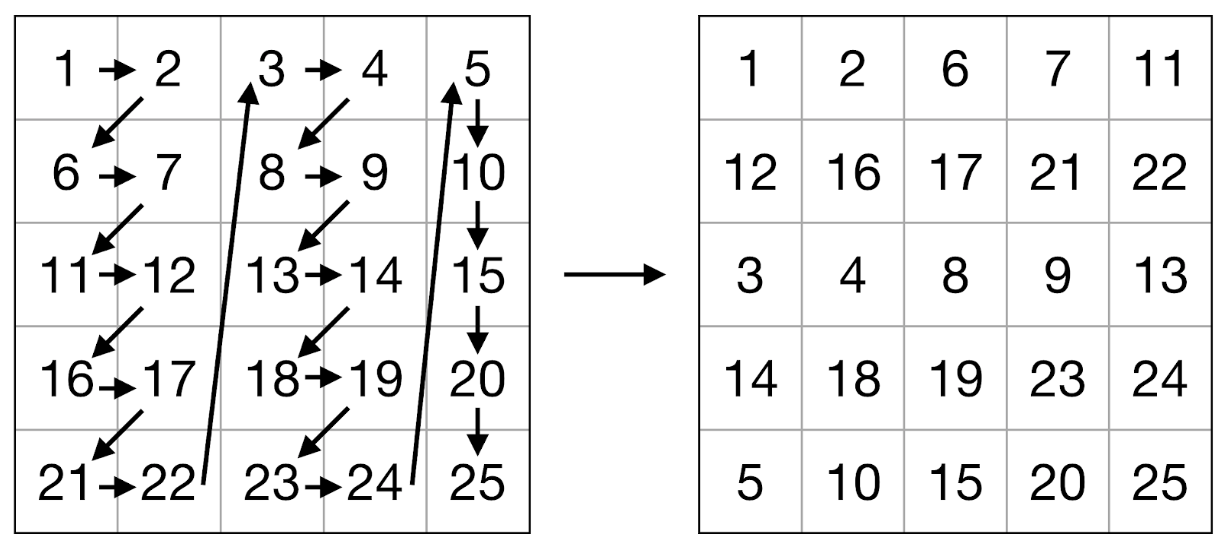
Рис. 2. Схема упаковки левой матрицы.
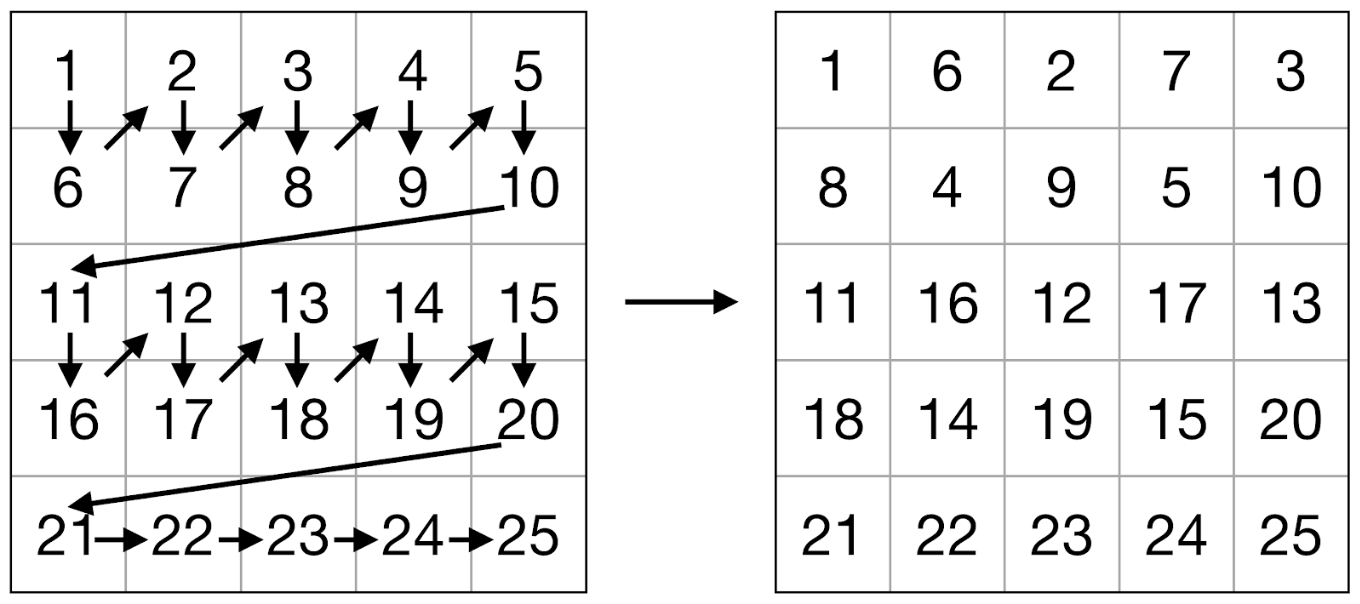
Рис 3. Схема упаковки правой матрицы.
Предложенный алгоритм можно записать в виде псевдокода следующим образом:
for bl_r in block_r(rhs):
packed_r <- pack_rhs(bl_r)
for bl_l in block_l(lhs):
packed_l <- pack_lhs(bl_l)
packed_res <- pack_res(bl_res)
kernel(packed_res, packed_l, packed_r)
bl_res <- unpack_res(packed_res)При этом lhs и rhs — левый и правый операнд матричного умножения соответственно, block_l(.), block_r(.) — методы, которые осуществляют разбиение на блоки lhs и rhs соответственно. Методы pack_rhs и pack_lhs реализуют упаковку блоков матриц, pack_res — упаковку результата, а unpack_res — распаковку результата. Метод kernel выполняет вычисления над упакованными блоками и помещает их в упакованный блок результата.
Псевдокод метода kernel приведен ниже:
for j in {0, ..., cols / nr}
{dst0, dst1} <- следующий блок результата
for i in {0, ..., rows / mr}
for k in {0, ..., depth / 2}
bl_r <- следующий блок правой матрицы
bl_l <- следующий блок левой матрицы
lhs <- pshufb(zero, bl_l, 0x0901080009010800LL)
rhs0 <- punpcklbh(zero, bl_r)
rhs1 <- punpckhbh(zero, bl_r)
dst0 <- dst0 + pmaddh(rhs0, lhs)
dst1 <- dst1 + pmaddh(rhs1, lhs);
// Обработка оставшихся элементовЗдесь pshufb — инструкция, перемешивающая элементы двух векторов согласно заданному правилу (магическое число на месте третьего аргумента), punpckhbh — инструкция, чередующая элементы старших половин входных 16-битных векторов, punpcklbh — инструкция, чередующая элементы младших половин входных 16-битных векторов, pmaddh — инструкция, выполняющая длинное умножение соответствующих элементов входных 16-битных векторов и последующее сложение соседних произведений.
В основном цикле программы дополнительно была выполнена раскрутка цикла с целью минимизации обращений в память за счёт использования регистров. Размер обрабатываемого блока результата составил nr х mr = 12 х 8.
В результате, одна итерация основного цикла занимает 8 тактов и обрабатывает 48 элементов результата. Для вещественного умножения длительность одной итерации цикла составляет 8 тактов для СК версии 3, поскольку загрузка данных выполняется за 14 команд буфера подкачки массивов, а вычисления — за 48 комбинированных команд умножение+сложение, которые распределяются по 8 широким командам.
В Таблице 2 приведены результаты замеров времени умножения двух 8-битных матриц предложенным способом и классического умножения на Эльбрус-4С, реализованного с использованием библиотеки высокопроизводительных функций EML. Каждое измерение было усреднено по N = 10^6 итерациям.
Таблица 2. Время работы умножения двух матриц А и В с помощью предложенной реализации и с помощью EML для матриц разных размеров.
| Размер А | Размер В | Время работы предложенной реализации, мс | Время работы EML, мс |
|---|---|---|---|
| 16x9 | 9х100 | 0.04 | 0.01 |
| 16x9 | 9х400 | 0.15 | 0.04 |
| 16x25 | 25x400 | 0.18 | 0.06 |
| 16x144 | 144x400 | 0.29 | 0.20 |
| 16x400 | 400x400 | 0.62 | 0.50 |
| 16x400 | 400x1600 | 2.57 | 2.07 |
| 32x400 | 400x1600 | 4.57 | 3.94 |
| 32x800 | 800x1600 | 13.91 | 11.88 |
| 32x800 | 800x2500 | 14.05 | 11.90 |
Можно видеть, что для Эльбрус-4С реализация целочисленного матричного умножения не превосходит по скорости высокооптимизированную вещественную реализацию за счет дополнительных затрат на упаковку данных. Для последующих поколений процессоров Эльбрус этот разрыв только усугубится вследствие увеличения количества АЛУ, работающих с вещественными числами.
Заключение
Мы рассмотрели популярную 8-битную нейросетевую модель, которая успешно используется на x86 и ARM, которые составляют большую часть процессорного рынка на сегодняшний день. До тех пор, пока не начнут появляться железки с нейропроцессорами в составе, это самый широкий класс пользовательских устройств, на которых запускается распознавание. Однако ускорение при использовании 8-битных коэффициентов в нейронной сети не является ее неотъемлемым свойством и сильно привязано к архитектуре вычислителя. Так, оказалось, что архитектура Эльбрус хорошо приспособлена для вещественных вычислений (в плане числа вычислителей она лучше, чем x86 и ARM), а вот с операциями над целыми числами все не так хорошо: она предоставляет до 6 64-битных вещественных АЛУ, в то время как АЛУ для векторных целочисленных операций (64 или 128 битных) доступны лишь на 2 из 6 каналов процессора.
Тем не менее, мы реализовали умножение 8-битных матриц с 32-битными результатами промежуточных вычислений. Эта реализация оказалась сравнимой по вычислительной производительности с оптимизированной вещественной реализацией для процессоров с СК версии 3 (Эльбрус-4С), но не превосходит ее для процессоров с СК версий 4 и 5 (Эльбрус-8С и Эльбрус-8СВ).
Что это значит? Мы в очередной раз убедились, что архитектура целевого устройства крайне важна и должна учитываться при разработке. Так, уже ставшие привычными вычисления в целых числах плохо “ложатся” на Эльбрусы потому, что его вещественная производительность не ниже целочисленной. Это хорошо для каких-то алгоритмов и представляет трудности для других, поэтому при обсуждении методов повышения производительности не стоит забывать об особенностях оборудования. Ну а мы все еще можем ускорять сетки иначе, например, уменьшая число коэффициентов и/или упрощая их структуру.
Есть ли какой-то смысл в 8-битных моделях на Эльбрусе? Ну, возможно в экзотических ситуациях, когда необходимо экономить память на запоминающем устройстве или сжать модель, чтобы она помещалась в кэш-память или оперативную память (если доступ к запоминающему устройству особо медленный).
P.S. Статья написана по материалам нашей журнальной публикации
Limonova E. E., Neyman-Zade M. I., Arlazarov V. L. Special aspects of matrix operation implementations for low-precision neural network model on the Elbrus platform // Вестник ЮУрГУ. Математическое моделирование и программирование. — 2020. — Т. 13. — № 1. — С. 118-128. — DOI: 10.14529/mmp200109.
- https://github.com/google/gemmlowp
- https://engineering.fb.com/ml-applications/qnnpack/
- Vanhoucke, Vincent, Andrew Senior, and Mark Z. Mao. "Improving the speed of neural networks on CPUs." (2011).
- K. Chellapilla, S. Puri, P. Simard. High Performance Convolutional Neural Networks for Document Processing // Tenth International Workshop on Frontiers in Handwriting Recognition. – Universite de Rennes, 1 Oct 2006. – La Baule (France). – 2006.
- Ким А.К., Перекатов В. И., Ермаков С. Г. Микропроцессоры и вычислительные комплексы семейства “Эльбрус”. – СПб.: Питер, – 2013. – 272 c.
- Ишин, П.А. Ускорение вычислений с использованием высокопроизводительных математических и мультимедийных библиотек для архитектуры Эльбрус / П.А. Ишин, В.Е. Логинов, П.П. Васильев // Вестник воздушно-космической обороны. – М.: Научно-производственное объединение “Алмаз” им. акад. А.А. Расплетина. – 2015. – No4 (8). – cc. 64-68.
- Limonova E. E., Skoryukina N. S., Neyman-Zade M. I. Fast Hamming Distance Computation for 2D Art Recognition on VLIW-Architecture in Case of Elbrus Platform // ICMV 2018 / SPIE. март 2019. Т. 11041. ISSN 0277-786X. ISBN 978-15-10627-48-2. 2019. Т. 11041. 110411N. DOI: 10.1117/12.2523101
- Goto, K. Anatomy of high-performance matrix multiplication / K. Goto, R.A. Geijn // ACM Transactions on Mathematical Software (TOMS) – 2008. – 34(3). – p.12.
Автор: SmartEngines







