Возможно, прозрачность не кажется какой-то интересной темой. Формат GIF, позволявший некоторым пикселям просвечивать сквозь фон, опубликован более 30 лет назад. Почти в каждом приложении для графического дизайна, выпущенном за последние два десятка лет, поддерживается создание полупрозрачного контента. Эти понятия давно перестали быть чем-то новым.
В своей статье я хочу показать, что на самом деле прозрачность в цифровых изображениях намного интереснее, чем кажется — в том, что мы воспринимаем как нечто само собой разумеющееся, есть невидимая глубина и красота.
Непрозрачность
Если вам когда-нибудь доводилось смотреть сквозь розовые очки, то вы могли видеть нечто подобное тому, что показано на рисунке ниже. [В оригинале статьи многие изображения интерактивны.] Попробуйте перемещать очки, чтобы посмотреть, как они влияют на то, что сквозь них видно:

Подобные очки работают следующим образом: они пропускают много красного цвета, приличное количество синего и совсем мало зелёного. Математику этих очков можно записать набором из трёх уравнений. Буква R обозначает результат операции, а буква D описывает точку, на которую мы смотрим. Индексы RGB обозначают красный, зелёный и синий компоненты:
RR = DR × 1.0
RG = DG × 0.7
RB = DB × 0.9
Это цветное стекло пропускает красный, зелёный и синий компоненты фона с разной силой. Иными словами, прозрачность розовых очков зависит от цвета падающего света. В общем случае прозрачность может варьироваться в зависимости от длины волны света, но в данном упрощённом примере нас интересует только то, как очки влияют на классические компоненты RGB.
Симуляция поведения обычных солнцезащитных очков гораздо проще, они обычно просто ослабляют падающий свет на какую-нибудь величину:

Эти очки пропускают только 30% проходящего через них света. Их поведение можно описать следующими уравнениями:
RR = DR × 0.3
RG = DG × 0.3
RB = DB × 0.3
Все три компонента цвета уменьшены на одинаковое значение — поглощение падающего света одинаково. Мы можем сказать, что тёмные очки на 30% прозрачны (transparent) или что они на 70% непрозрачны (opaque). Непрозрачность (Opacity) объекта определяет, сколько цвета он блокирует. В компьютерной графике мы обычно имеем дело с упрощённой моделью, в которой для описания этого свойства нужно только одно значение. Непрозрачность может пространственно варьироваться. как, например, столб дыма, который становится выше всё прозрачнее.
В реальном мире объекты с непрозрачностью 100% просто непрозрачны и они не пропускают света вообще. Мир цифровых изображений немного отличается. В нём есть пограничные случаи, когда даже сплошные непрозрачные предметы пропускают определённое количество света.
Покрытие
Векторная графика имеет дело с чёткими и бесконечно точными описаниями фигур, задаваемыми при помощи точек. отрезков прямых, кривых Безье и других математических примитивов. Когда нужно выводить фигуры на экран компьютера, эти безукоризненные сущности приходится растеризировать в битовую карту:

Растеризация векторной фигуры в битовую карту
Самый примитивный способ растеризации заключается в проверке того, где находится сэмпл пикселя — внутри или снаружи векторной фигуры. В показанных ниже примерах можно перетаскивать треугольник, в увеличенном виде движения будут более точными. Синий контур обозначает исходную векторную геометрию. Как видите, лесенка на краях треугольника выглядит некрасиво и сильно мерцает при перемещении геометрии:
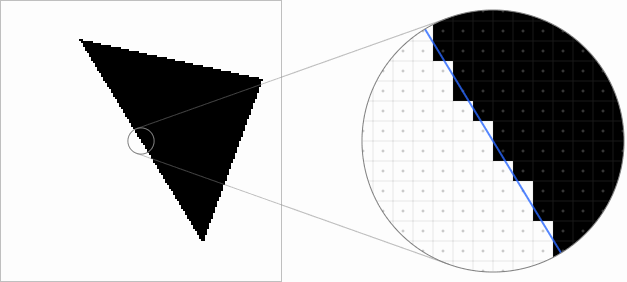
Недостаток такого подхода заключается в том, что мы выполняем только одну проверку на каждый выводимый пиксель, и результаты дискретизируются на одно из двух возможных значений — внутри или снаружи.
Можно сэмплировать векторную геометрию несколько раз на пиксель, чтобы получить большую градацию шагов и решить, что некоторые пиксели закрыты только частично. Одно из возможных решений: использовать четыре точки сэмплирования, позволяющие представить пять уровней покрытия: 0, 1⁄4, 2⁄4, 3⁄4 и 1:
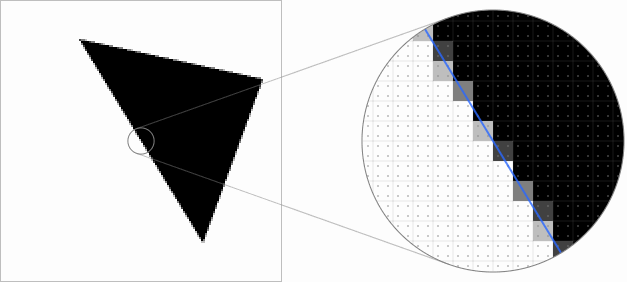
Качество краёв треугольника улучшилось, но всего пяти возможных уровней покрытия часто недостаточно и мы можем запросто добиться гораздо лучшего результата. Хотя на представление пикселя как маленького квадрата в мире обработки сигналов смотрят с неодобрением, в некоторых контекстах это полезная модель, позволяющая нам вычислять точное покрытие пикселя векторной геометрией. Пересечение линии и квадрата всегда можно разложить на трапецию и прямоугольник:

Отрезок прямой делит квадрат на трапецию и прямоугольник
Можно достаточно легко вычислить площадь обеих частей, а их сумма, поделённая на площадь квадрата, определяет процент покрытия пикселя. Таким образом покрытие вычисляется как точное число с произвольной точностью. В показанной ниже демонстрации этот метод используется для рендеринга гораздо более качественных краёв, которые остаются плавными даже при перетаскивании треугольника:
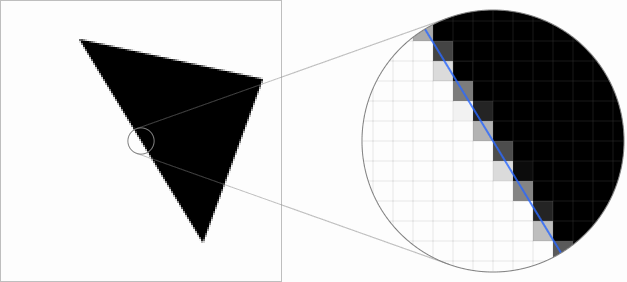
Когда дело доходит до более сложных фигур, например, эллипсов или кривых Безье, то их очень часто подразделяют на простые отрезки прямых, позволяющие вычислять покрытие с нужной точностью.
Концепция частичного покрытия критически важна для высококачественного рендеринга векторной графики и, что более важно, для рендеринга текста. Если вы сделаете скриншот этой статьи и рассмотрите его внимательно, то заметите, что почти все края глифов покрывают пиксели только частично:
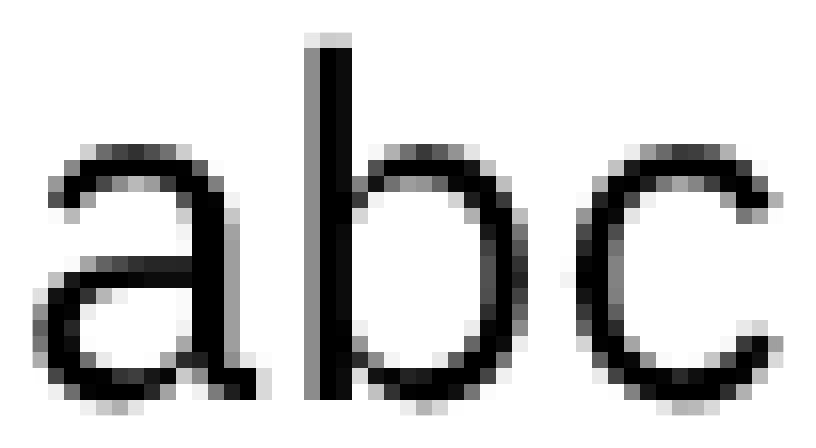
В рендеринге текста активно применяется частичное покрытие
Имея непрозрачность объекта и покрытие им отдельных пикселей, можно соединить их в одно значение.
Альфа
Произведение непрозрачности объекта и его покрытия пикселя называется альфой:
альфа = непрозрачность × покрытие
Объект с непрозрачностью 60%, покрывающий 30% площади пикселя, имеет в этом пикселе значение альфы 18%. Естественно, что когда объект прозрачен или совершенно не покрывает пиксель, то значение альфы в этом пикселе равно 0. После перемножения различия между непрозрачностью и покрытием пропадают, что в некотором смысле оправдывает то, что понятия «альфа» и «непрозрачность» используются как синонимы.
Альфу часто представляют в виде четвёртого канала битового изображения. Обычные значения красного, зелёного и синего дополняются значением альфы, образуя четвёрку значений RGBA.
Когда дело доходит до хранения значений альфы в памяти, есть искушение использовать для этого всего несколько бит. В случае покрытия пикселей краёв непрозрачных объектов кажется, что вполне достаточно будет 4 или даже 3 битов, в зависимости от плотности пикселей экрана:
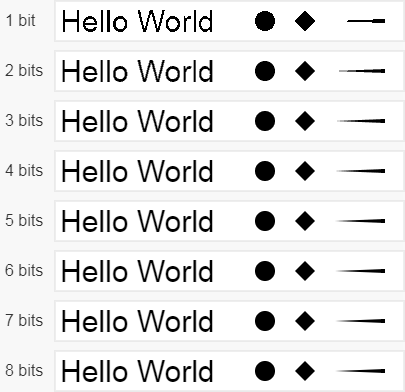
Однако непрозрачность тоже влияет на значение альфы, поэтому низкая битовая глубина может стать катастрофической в некоторых случаях плавно меняющейся прозрачности. На изображении ниже показан градиент от непрозрачного чёрного до белого цвета, который демонстрирует, что низкая битовая глубина приводит к очень сильным перепадам цвета:
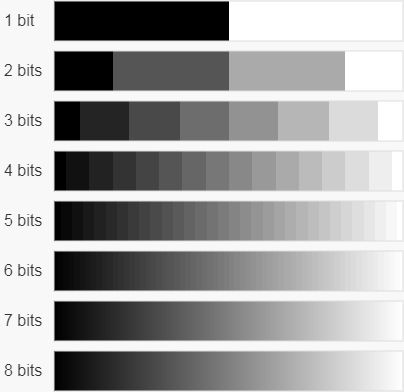
Очевидно, что чем больше бит, тем лучше, и чаще всего для альфы используется битовая глубина 8 для соответствия точности компонентов цвета, из-за чего многие RGBA-буферы занимают по 32 бита на пиксель. Стоит также заметить, что в отличие от компонентов цвета, которые часто кодируются при помощи нелинейного преобразования, альфа хранится линейно — закодированное значение 0.5 соответствует значению альфы 0.5.
Говоря про альфу, мы пока совершенно игнорировали все остальные компоненты цвета, но кроме блокирования фонового цвета пиксель может сам добавлять немного цвета. Идея достаточно проста — полупрозрачный розовый объект блокирует часть поступающего фонового освещения и испускает или отражает немного розового света:

Заметьте, что он ведёт себя не так, как цветное стекло. Стекло просто блокирует часть фонового освещения с различной яркостью. Если посмотреть на абсолютно чёрный объект через розовое стекло, то его чернота сохранится, потому что чёрный объект не испускает и не отражает никакого света. Однако полупрозрачный розовый объект добавляет своего собственного света. Если разместить его поверх чёрного объекта, то результат окажется розоватым. Хорошим аналогом такого поведения является взвешенный в воздухе мелкий материал, например дымка, дым, туман или какой-нибудь цветной порошок.
Визуализировать альфа-канал немного труднее — идеально прозрачный объект невидим по определению, поэтому чтобы различать объекты, нам нужно воспользоваться двумя трюками. Шахматный фон показывает, какие части изображения прозрачные; этот паттерн используется во многих графических приложениях:

Шахматный паттерн показывает прозрачные части
Четыре небольших квадрата под изображением сообщают нам, что мы видим красный, зелёный, синий и альфа-компонент изображения. В некоторых случаях полезно непосредственно видеть значения альфа-канала, и проще всего отобразить их при помощи оттенков серого:

Отображение значений RGB и A на разных поверхностях
Чем ярче оттенок серого, тем выше значение альфы, то есть чистый чёрный соответствует 0% альфы, а чистый белый — 100% альфы. Небольшие квадраты показывают, что компоненты RGB и A изображения разделены на две части.
Сам по себе альфа-компонент не особо полезен, но он становится очень важным, когда мы говорим о композитинге.
Простой композитинг
Очень немногие эффекты 2D-рендеринга можно реализовать одной операцией, и для создания готового результата мы используем процесс композитинга, сочетающего различные изображения. Например, простую кнопку “Cancel” можно создать композитингом пяти отдельных элементов:

Элементы композитинга кнопки “Cancel”
Композитинг часто выполняется в несколько этапов, на каждом из которых комбинируются два изображения. Используемое в композитинге изображение переднего плана обычно называют source. Используемое в композитинге фоновое изображение, на которое накладывается source, обычно называют destination.
Мы начнём с композитинга на непрозрачный фон, потому что это очень распространённый случай. Всё, что вы видите на экране в конечном итоге накладывается композитингом на непрозрачный destination.
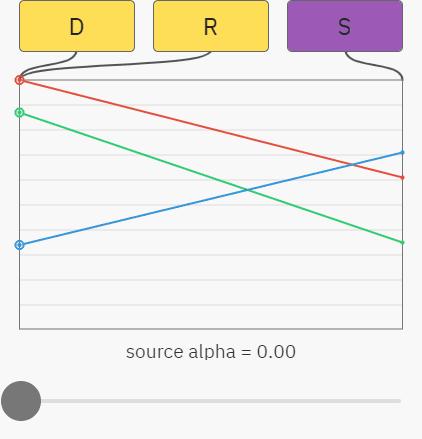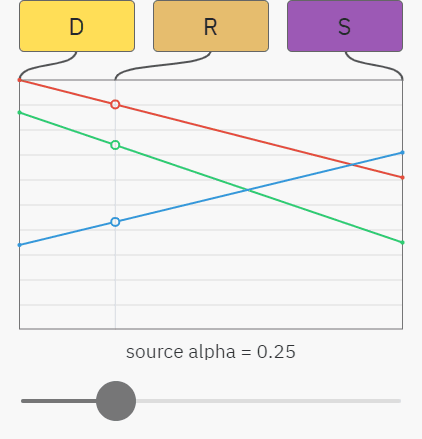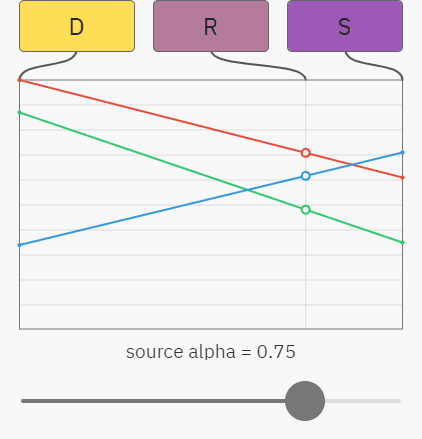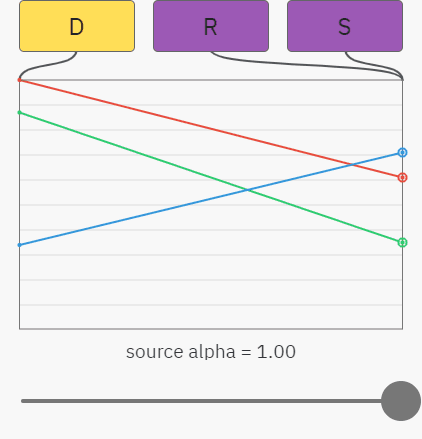
Когда значение альфы у source равно 100%, то source непрозрачен и должен полностью закрывать destination. Если значение альфы равно 0%, то source полностью прозрачен и он никак не влияет на destination. Значение альфы 25% позволяет объекту испустить 25% своего света и пропускает 75% света от фона, и так далее:

Композитинг фиолетовых source с разными значениями альфы на жёлтый destination
Вы можете уже понять, к чему всё идёт — простой случай альфа-композитинга на непрозрачный фон — это просто линейная интерполяция между цветами destination и source. На показанном ниже графике ползунок управляет значением альфы source, а красный, зелёный и синий графики отображают значения RGB-компонентов. Результат R — это просто смешение между source S и destination D:
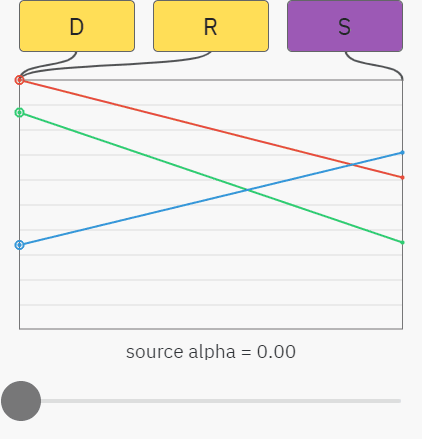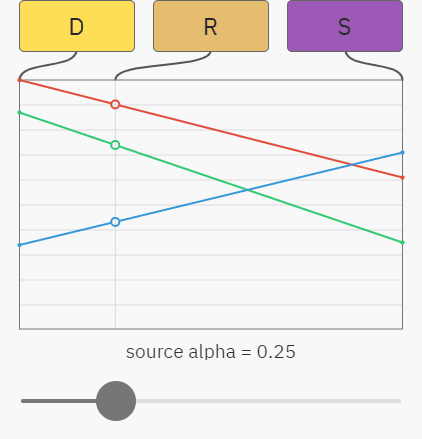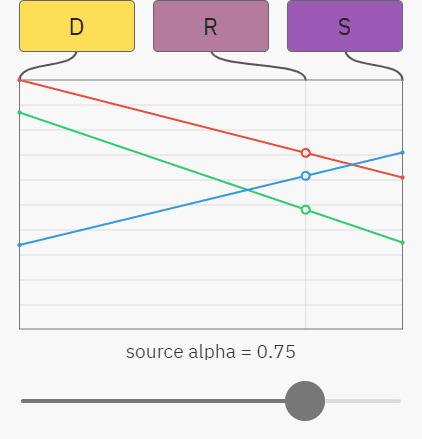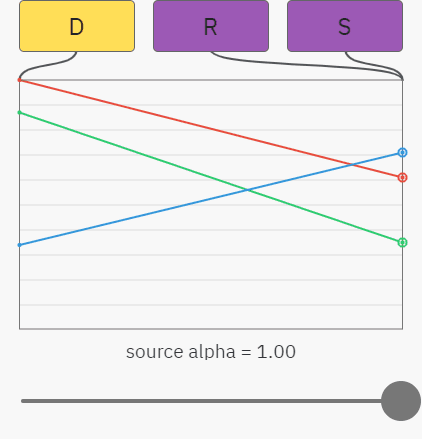
Происходящее здесь можно описать показанными ниже уравнениями. Как и раньше, индекс обозначает компонент, то есть SA — это значение альфы в source, а DG — значение зелёного в destination:
RR = SR × SA + DR × (1 − SA)RG = SG × SA + DG × (1 − SA)
RB = SB × SA + DB × (1 − SA)
Уравнения для красного, зелёного и синего компонентов имеют одинаковый вид, поэтому можно просто использовать индекс RGB и соединить их в одну строку:
RRGB = SRGB × SA + DRGB × (1 − SA)
Более того, поскольку destination непрозрачен и уже блокирует весь фоновый свет, мы знаем, что значение альфы у результата всегда равно 1:
RA = 1
Композитинг на непрозрачный фон выполняется просто, но он довольно ограничен в возможностях. Во многих случаях требуется более надёжное решение.
Промежуточные буферы
На изображении ниже показан двухэтапный процесс композитинга трёх разных слоёв, помеченных как A, B и C. Символ ⇨ будет обозначать «накладывается композитингом на»:

Результат двухэтапного композитинга трёх слоёв
Сначала мы накладываем композитингом B на C, а затем накладываем на них A, чтобы получить готовое изображение. В следующем примере мы выполним всё немного иначе. Сначала мы соединим композитингом два верхних слоя, а затем наложим результат на последний destination:

Результат двухэтапного композитинга трёх слоёв в другом порядке
Вы наверно задаётесь вопросом, возникает ли такая ситуация на практике, но на самом деле она очень распространена. Многие нетривиальные операции композитинга и эффекты рендеринга, например, маскирование и размытие, требуют проходить через промежуточный буфер, содержащий только частичные результаты композитинга. Эта концепция имеет разные названия: внеэкранные проходы (offscreen passes), слои прозрачности (transparency layers) или побочные буферы (side buffers), но обычно в их основе лежит одинаковая идея.
Для нас важнее то, что почти любое изображение с прозрачностью можно воспринимать как частичный результат какого-нибудь рендеринга, который позже будет наложен композитингом на последний destination:
Частичный композитинг кнопки в буфер
Нам нужно понять, как заменить композитинг полупрозрачных изображений A и B одним изображением (A⇨B), имеющим тот же цвет и непрозрачность. Давайте начнём с вычисления значения альфы конечного буфера.
Комбинирование значений альф
Возможно вам будет непонятно, как комбинировать непрозрачность двух объектов, но проще рассуждать об этой задаче, если мы вместо этого будем говорить о прозрачности.
Допустим, некое количество света проходит через первый объект, а затем через второй объект. Если прозрачность первого объекта равна 80%, то он пропустит 80% падающего света. Аналогично этому, второй объект с прозрачностью 60% пропустит 60% проходящего через него света, что даёт нам 60% × 80% = 48% от исходного света. Можете поэкспериментировать с прозрачностью в оригинале статьи; не забывайте, что ползунки управляют прозрачностью, а не непрозрачностью объектов на пути света:
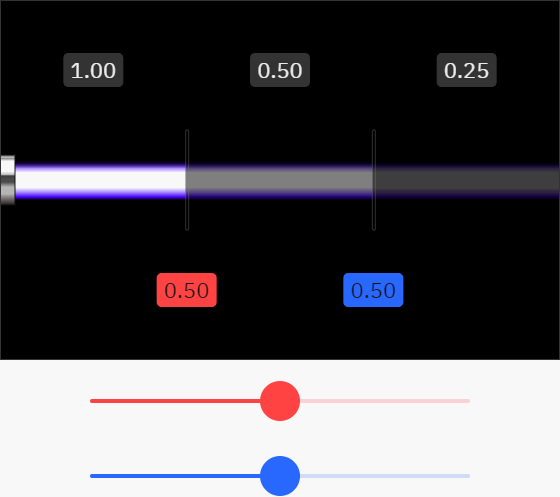
Естественно когда или первый, или второй объект непрозрачны, никакой свет через них не проходит, даже другой полностью прозрачен.
Если объект D имеет прозрачность DT, а объект S имеет прозрачность ST, то окончательная общая прозрачность RT этих двух объектов равна их произведению:
RT = DT × ST
Однако прозрачность — это просто единица минус альфа, поэтому подстановка даёт нам следующее:
1 − RA = (1 − DA) × (1 − SA)
Это выражение можно развернуть в такое:
1 − RA = 1 − DA − SA + DA × SA
И упростить так:
RA = DA + SA − DA × SA
Его можно сократить до одного из двух аналогичных видов:
RA = SA + DA × (1 − SA)
RA = DA + SA × (1 − DA)
Вскоре мы увидим, что чаще используется второй. Интересно также заметить, что получившееся значение альфы не зависит от относительного порядка объектов — непрозрачность получившихся пикселей одинакова, даже если поменять source и destination местами. Это очень логично. Свет проходящий через два объекта, должен затухать одинаково, с какой стороны бы о ни светил: спереди или сзади.
Комбинирование цветов
Вычислить альфу оказалось не так сложно, поэтому давайте попробуем разобраться в вычислениях RGB-компонентов. Изображение source имеет цвет SRGB, но его непрозрачность SA заставляет учитывать в готовом результате только произведение этих двух значений:
SRGB×SA
Изображение destination имеет цвет DRGB, непрозрачность заставляет его испускать свет DRGB×DA, однако часть света блокируется непрозрачностью изображения S, поэтому всё влияние destination равно:
DRGB×DA×(1 − SA)
Общий вклад света от S и D равен их сумме:
SRGB×SA + DRGB×DA×(1 − SA)
Аналогично, вклад объединённых слоёв равен их цвету, умноженному на их непрозрачность:
RRGB×RA
Мы хотим, чтобы эти два значения совпадали:
RRGB×RA = SRGB×SA + DRGB×DA×(1 − SA)
Что даёт нам окончательные уравнения:
RA = SA + DA × (1 − SA)
RRGB = (SRGB×SA + DRGB×DA×(1 − SA)) / RA
Посмотрите, насколько сложным получилось второе уравнение! Заметьте, что для получения значений RGB результата нам нужно выполнить деление на значение альфы. Однако для последующего этапа композитинта снова потребуется умножение на значение альфы, потому что результат текущей операции станет новым source или destination следующей операции. Это просто некрасиво.
Давайте на секунду вернёмся к почти финальному виду RRGB:
RRGB×RA = SRGB×SA + DRGB×DA×(1 − SA)
Source, destination и результат умножаются на их альфа-компоненты. Это даёт нам понять, что цвету и альфе пикселя «нравится» быть вместе, поэтому нужно сделать шаг назад и переосмыслить способ хранения информации о цвете.
Premultiplied Alpha
Вспомните, что мы говорили о непрозрачности — если объект частично непрозрачен, то его вклад в результат тоже будет частичным. Концепция Premultiplied alpha («предварительное умножение на альфу») реализует эту идею. Значения RGB-компонентов, как понятно из названия, предварительно умножаются на альфа-компонент. Начнём с цвета без предварительного умножения:
(1.00, 0.80, 0.30, 0.40)
Предварительное умножение на альфу даёт нам следующее:
(0.40, 0.32, 0.12, 0.40)
Давайте взглянем на несколько пикселей одновременно. На рисунке ниже показано, как информация о цвете хранится без предварительного умножения альфы:

Информация RGB и A в изображении без предварительного умножения
Заметьте, что области, где альфа равна 0, могут иметь произвольные значения RGB, как видно по зелёным и голубым глитчам на изображении. В случае предварительного умножения на альфу информация о цвете также хранит значения непрозрачности пикселя:

Информация RGB и A в предварительно умноженном изображении
Premultiplied alpha иногда называют associated alpha, а не-premultiplied alpha иногда называют straight или unassociated alpha.
Когда альфа-компонент цвета равен 0, предварительное умножение обнуляет все остальные компоненты, вне зависимости от их значений:
(0.0, 0.0, 0.0, 0.0)
В случае premultiplied alpha существует только один полностью прозрачный цвет, и это очаровательно.
Преимущества подобной обработки компонентов цвета постепенно станут вам понятны, но прежде чем мы вернёмся к примеру с композитингом, давайте посмотрим, как premultiplied alpha помогает решать некоторые другие проблемы рендеринга.
Фильтрация
Гауссово размытие — это популярный способ создания интересного расфокусированного фона или снижения высокой частоты фоновой части содержимого некоторых элементов UI. Как мы увидим, предварительное умножение альфы критически важно для создания правильно выглядящего размытия.
Изображение, которое мы будем анализировать, создано заполнением фона непрозрачным на 1% синим цветом, поверх которого нарисован непрозрачный красный круг. Сначала давайте рассмотрим пример без предварительного умножения. Я отделил каналы RGB от канала альфы, чтобы было понятно, что происходит. Стрелка обозначает операцию размытия:
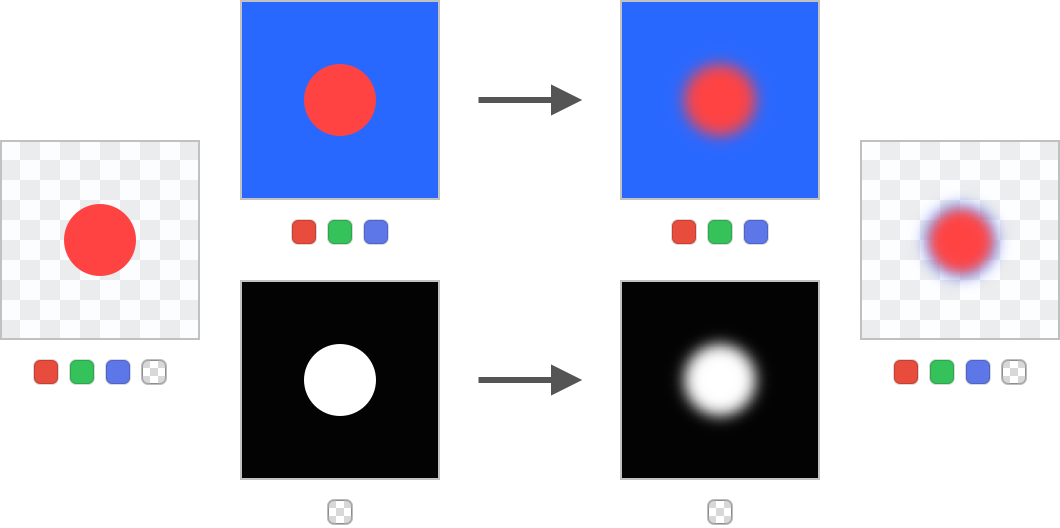
Размытие содержимого без предварительного умножения
Готовый результат имеет некрасивое синее гало. Так получилось, потому что синий фон просочился на красную область во время размытия и уже потом, во время композитинга, к нему был добавлен вес альфы.
Когда цвета предварительно умножены на альфу, результат получается правильным:
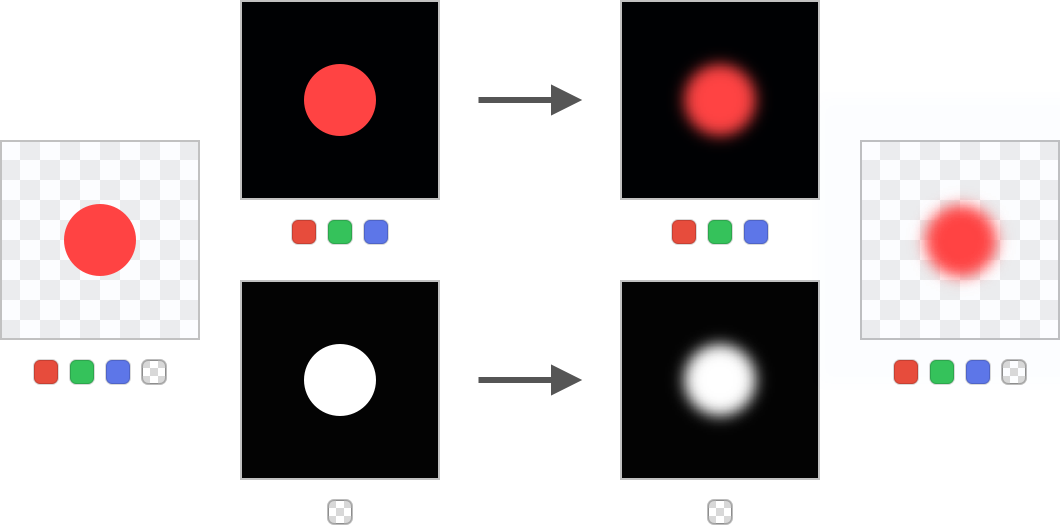
Размытие предварительно умноженного содержимого
Из-за предварительного умножения синий цвет изображения уменьшается до 1% от его исходной силы, поэтому его влияние на цвета размытого круга чрезвычайно мало.
Интерполяция
Рендеринг изображения, пиксели которого идеально сопоставляются с destination — это простая задача, потому что между сэмплами нам нужно выполнять тривиальное сопоставление «один к одному». Проблема возникает, когда не существует простого сопоставления, например, из-за поворота, масштабирования или переноса. На рисунке ниже видно, что пиксели повёрнутого изображения, обозначенные красным контуром, больше не соответствуют destination:

Относительная ориентация изображения и пиксели destination до и после поворота
Существует множество способов выбора цвета из изображения, который должен быть записан в пиксель destination, и самый простой из них — это так называемая «интерполяция по ближайшему соседу» (nearest-neighbor interpolation), при которой в качестве конечного пикселя просто выбирается ближайший сэмпл в текстуре.
В показанной ниже демонстрации красным контуром показана позиция изображения в destination. Справа показаны позиции сэмплов с точки зрения изображения. Перетаскивая ползунок (в оригинале статьи), можно поворачивать четырёхугольник и наблюдать за тем, как сэмплы выбирают цвета из битовой карты. Я выделил один пиксель в source и destination, чтобы их связь была нагляднее:
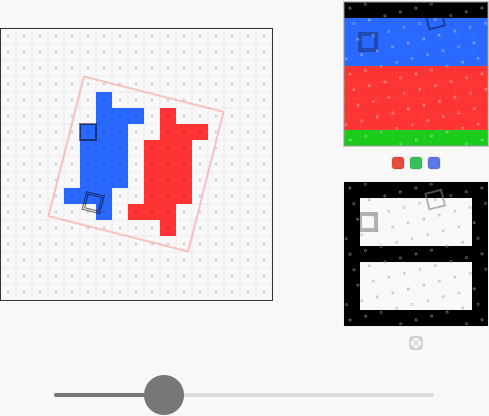
Такое решение вполне функционально и пиксели имеют целостную окраску, но качество при этом оказывается неприемлемым. Лучше будет использовать билинейную интерполяцию, вычисляющую взвешенное среднее четырёх ближайших пикселей сэмплируемого изображения:
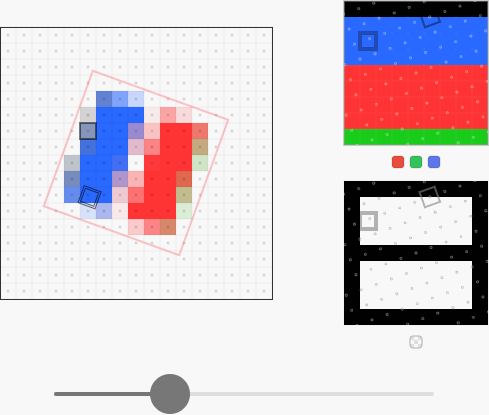
Так получается лучше, но края вокруг прямоугольников выглядят неправильно, содержимое пикселей без умножения сливается, потому что альфа «применяется» после интерполяции. Рекомендуемое иногда решение слияния цвета верного содержимого, которое показано в потрясающей статье Адриана Корреже [перевод на Хабре], далеко от идеала — ни один цвет в зазоре между красным и синим прямоугольниками не будет выглядеть правильно.
Давайте посмотрим, как всё будет выглядеть при изображении с premultiplied alpha и композитинге с усовершенствованной формулой, которую мы вскоре выведем:
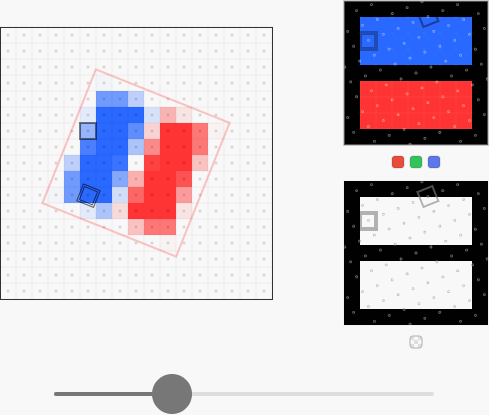
Просто идеально — мы избавились от всех слияний цветов и нигде не видно зубцов.
В конечном итоге, проблемы, связанные с размытием и интерполяцией, тесно связаны. Любая операция, требующая какого-либо комбинирования полупрозрачных цветов, без предварительного умножения цветов на альфу скорее всего даст неверные результаты.
Правильный композитинг
Вернёмся к композитингу. Мы остановились на почти выведенном уравнении:
RRGB×RA = SRGB×SA + DRGB×DA×(1 − SA)
Если представить цвета при помощи premultiplied alpha, то все эти неудобные умножения пропадут, потому что альфа уже будет являться частью значений цветов. Тогда мы получим следующее:
RRGB = SRGB + DRGB×(1 − SA)
Давайте рассмотрим уравнение альфы:
RA = SA + DA × (1 − SA)
Коэффициенты для красного, зелёного, синего и альфа-каналов одинаковы, поэтому мы можем выразить всё выражение одним уравнением и просто запомнить, что каждый компонент подвергается одинаковой операции:
R = S + D × (1 − SA)
Посмотрите, насколько premultiplied alpha всё упростила. Когда мы анализируем компоненты уравнения, все они находятся на своём месте. Операция маскирует часть фонового света и прибавляет новый свет:
R = S + D × (1 − SA)
Такую операцию смешения называют source-over, sover или просто normal, и она, без всяких сомнений, является самым распространённым режимом композитинга. Почти всё, что вы видите на моём веб-сайте, смешано в этом режиме.
Ассоциативность
Важным свойством source-over, выполняемым над предварительно умноженными на альфу цветами, является ассоциативность этой операции. Благодаря нему в сложном уравнении смешения мы можем расставлять скобки совершенно произвольно. Все показанные ниже композиции эквивалентны:
R = (((A⇨B)⇨C)⇨D)⇨E
R = (A⇨B)⇨(C⇨(D⇨E))
R = A⇨(B⇨(C⇨(D⇨E)))
Доказательство этого достаточно просто, но я не буду нагружать вас алгебраическими манипуляциями. На практике это значит, что мы можем выполнять частичный рендеринг сложных рисунков, не боясь, что финальная композиция будет выглядеть неверно.
В подавляющем большинстве случаев альфа используется только для композитинга при помощи source-over, однако её преимущества на этом не заканчиваются. Значения альфы можно использовать и для других полезных операций рендеринга.
Композитинг Портера-Даффа
В июле 1984 года Томас Портер и Том Дафф опубликовали оригинальную статью “Compositing Digital Images”. Авторы не только впервые ввели понятие premultiplied alpha и вывели уравнение композитинга source-over, но и представили целое семейство операций альфа-композитинга, многие из которых малоизвестны, хоть и очень полезны. Новые функции также называют операторами, потому что аналогично сложению или умножению они выполняют действия с входными значениями для создания выходного значения.
Over
В дальнейших примерах мы будем использовать интерактивные демо, показывающие операции различных режимов смешения. Изображением destination будет чёрный символ «треф», а изображением source будет красный символ «червей». Можно перетаскивать сердце по изображению и наблюдать, как накладываемые друг на друга фигуры ведут себя при разных операторах композитинга. Обратите внимание на небольшую мини-карту в углу. Некоторые режимы смешения очень разрушительны и легко запутаться в происходящем. На мини-карте всегда показывается результат простого композитинга source-over, упрощающий понимание:

R = S + D × (1 − SA)
R = S × (1 − DA) + D
Если переключиться в destination-over, то вы сразу поймёте, что он просто «переворачивает» source-over — destination и source меняются в уравнении местами и результат эквивалентен тому, что мы будем считать destination изображением source. Хотя он кажется излишним, оператор destination-over чрезвычайно полезен, потому что он позволяет выполнять композитинг объектов, находящихся под уже существующим содержимым.
Out
Операторы source-out и destination-out отлично подходят для пробивания отверстий в source или destination:
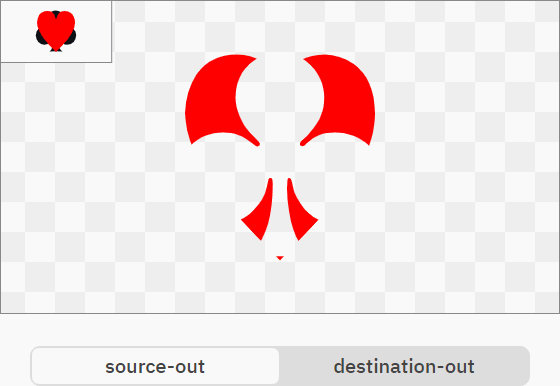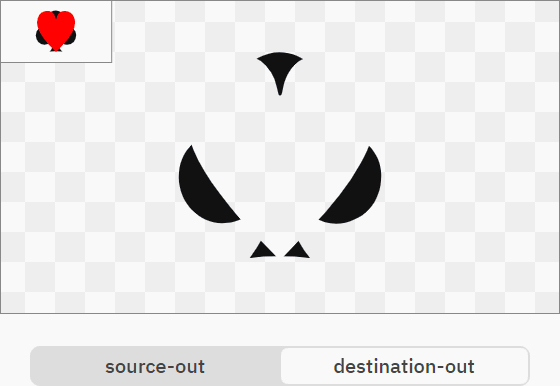
R = S × (1 − DA)
R = D × (1 − SA)
Из этих двух операторов более удобным является Destination-out, потому что использует альфа-канал для пробивания отверстий в форме destination.
In
Операторы source-in и destination-in по сути являются операторами маскирования:
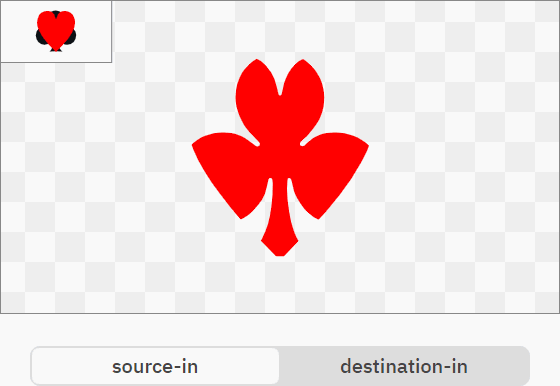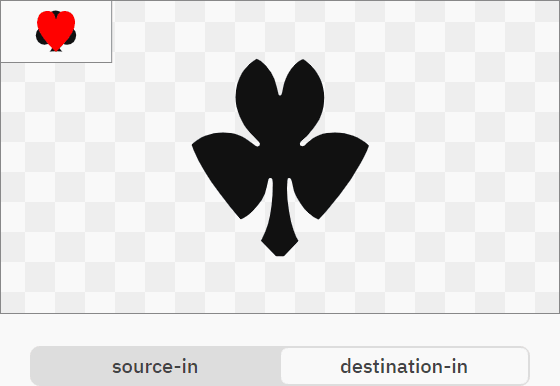
R = S × DA
R = D × SA
Они позволяют довольно просто создавать сложные пересечения нетривиальной геометрии без разрешения относительно трудных в вычислении пересечений векторных контуров.
Atop
Операторы source-atop и destination-atop позволяют накладывать новое содержимое на уже существующее, одновременно маскируя его по контуру destination:

R = S × DA + D × (1 − SA)
R = S × (1 − DA) + D × SA
Xor
Оператор исключающего ИЛИ (xor) сохраняет или source, или destination, а их совпадающие области исчезают:

R = S × (1 − DA) + D × (1 − SA)
Source, Destination, Clear
Последние три классических режима композитинга довольно скучны. Source, также называемый copy, просто берёт цвет source. Аналогично, destination игнорирует цвет source и просто возвращает destination. Оператор clear просто всё очищает:
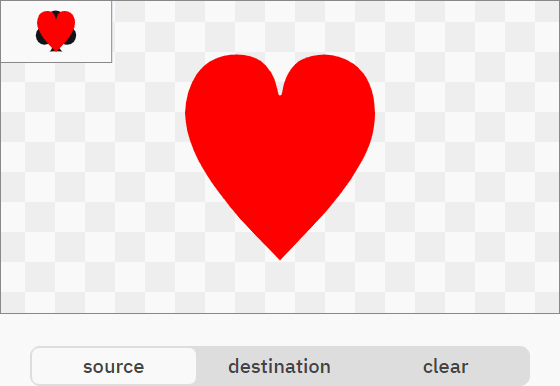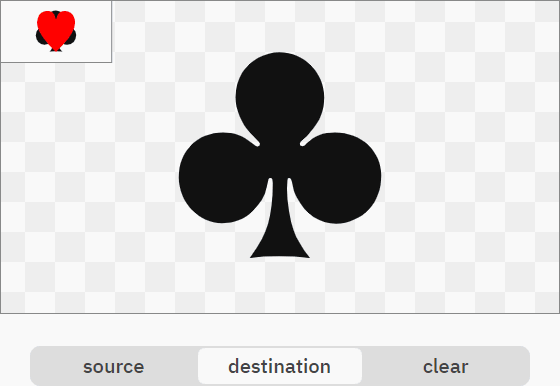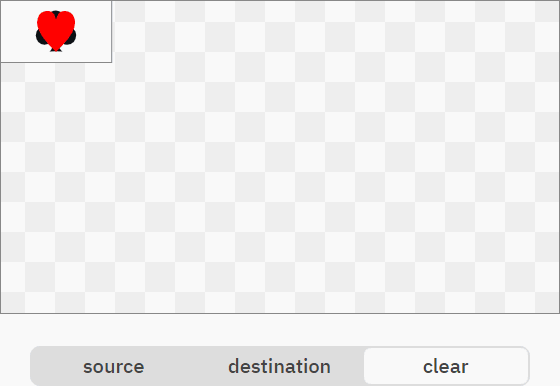
R = S
R = D
R = 0
Применимость этих режимов ограничена. При помощи clear можно сбрасывать заполненный буфер, но эту операцию можно оптимизировать, просто заполнив память нулями. Кроме того, в некоторых случаях source может быть экономнее в вычислениях, потому что он не требует никакого смешивания, а просто заменяет содержимое буфера информацией source.
Портер-Дафф в действии
Разобравшись с отдельными операторами, давайте посмотрим, как можно их сочетать. В показанном ниже примере мы нарисуем морской логотип, не пользуясь маскированием или сложными геометрическими фигурами. Синие контуры показывают создаваемую простую геометрию. Перемещаться по этапам можно, нажимая на правую часть изображения, а возвращаться назад, нажимая на левую:
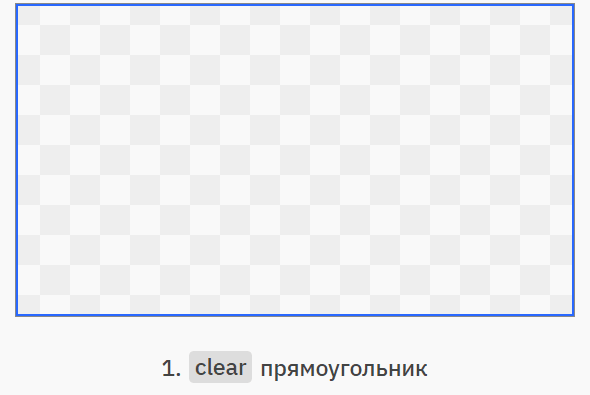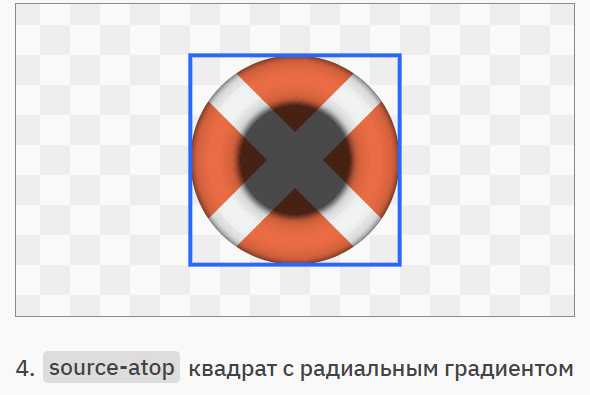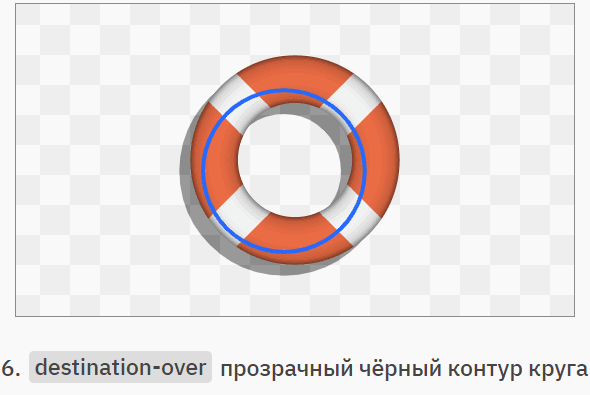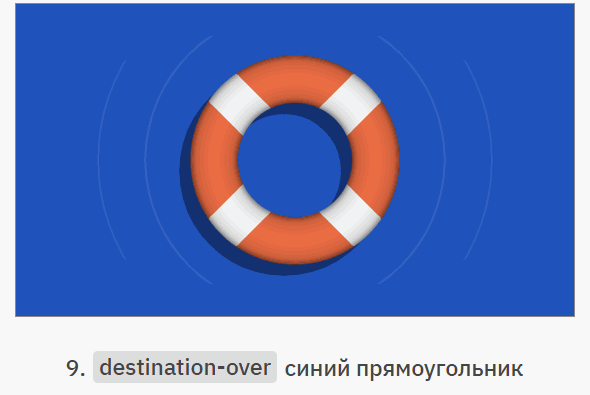
Разумеется, мы ни в коем случае не обязаны отказываться от масок и контуров усечения, но о таком инструменте, как режимы композитинга Портера-Даффа часто забывают, хотя с их помощью гораздо проще создавать некоторые визуальные эффекты.
Операторы
Если присмотреться к операторам Портера-Даффа, то можно заметить, что все они имеют одинаковый вид. Source всегда умножается на некий коэффициент FS и прибавляется к destination, умноженному на коэффициент FD:
R = S×FS + D×FD
FS может принимать значения 0, 1, DA и 1 − DA, а FD может быть равным 0, 1, SA или 1 − SA. Не имеет смысла умножать source или destination на их собственные альфы, потому что они уже предварительно умножены, и мы просто получим причудливый, но не особо полезный эффект квадратичной альфы. Все операторы можно представить в виде таблицы:
| 0 | 1 | DA | 1 − DA | |
| 0 | clear | source | source-in | source-out |
| 1 | destination | destination-over | ||
| SA | destination-in | destination-atop | ||
| 1 − SA | destination-out | source-over | source-atop | xor |
Обратите внимание на симметрию операторов по диагонали. Четыре центральных элемента в таблице отсутствуют и так получилось потому, что они отличаются от остальных.
Аддитивное освещение
В своей статье Портер и Дафф представили ещё один оператор, при котором и FS, и FD равны 1. Он известен под названиями plus, lighter и plus-lighter:
R = S + D
Эта операция по сути прибавляет освещение source к destination:

Аддитивное освещение, реализованное при помощи оператора plus
Зелёный и красный правильно образуют жёлтый, а зелёный и синий образуют голубой (cyan). Чёрный цвет — это отсутствие операции, он никак не изменяет цветовые значения, потому что прибавление к числу нуля ничего не меняет.
Трём оставшимся операторам не дали названий, потому что они не особенно полезны. Они являются просто комбинацией маскирования и смешения.
Также стоит заметить, что premultiplied alpha позволяет нам использовать оператор source-over непредусмотренным образом. Давайте снова взглянем на уравнение:
R = S + D × (1 − SA)
Если нам удастся сделать значение альфы в source равным нулю, то при наличии ненулевых значений в RGB-каналах мы можем добиться аддитивного освещения без использования оператора plus:
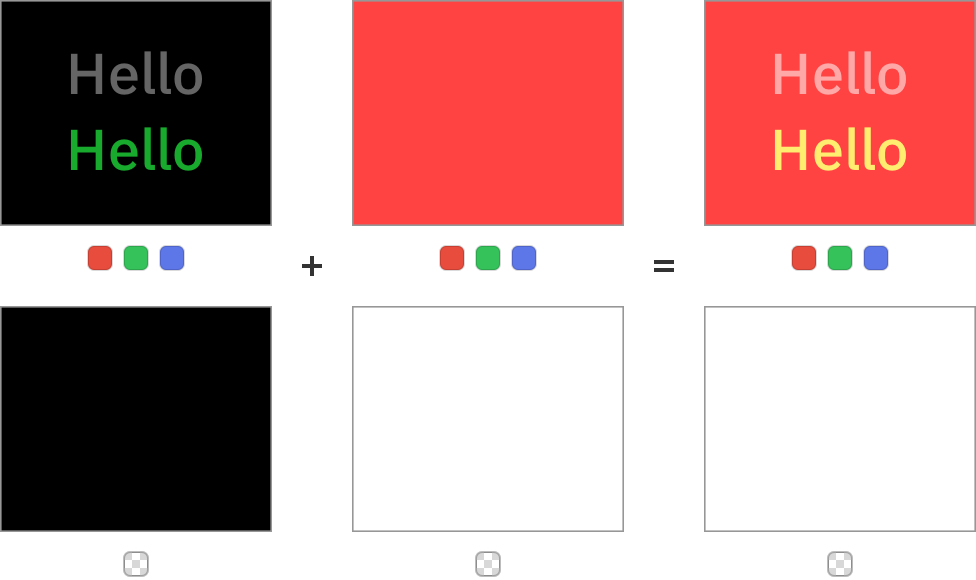
Аддитивное освещение, реализованное при помощи оператора source-over
Заметьте, что здесь надо быть аккуратными — значения больше не умножаются на альфу правильно. В некоторых программах может существовать оптимизация, полностью избегающая смешения цветов с нулевой альфой, а другие программы могут обратить предварительное умножение на значения альфы, выполнить какие-то операции с цветами, а затем снова предварительно умножить на альфу, что полностью уничтожит цветовые каналы. Также может оказаться сложным экспортировать в таком формате ресурсы, поэтому если у вас нет возможности полностью контролировать конвейер рендеринга, то стоит придерживаться оператора plus.
Все обсуждаемые нами элементы пока хорошо между собой сочетались. А теперь давайте «снимем розовые очки» и обсудим некоторые проблемы, которые нужно учитывать при работе с альфа-композитингом.
Групповая непрозрачность
Давайте взглянем на этот простой рисунок пилюли, составленный всего из шести примитивов:
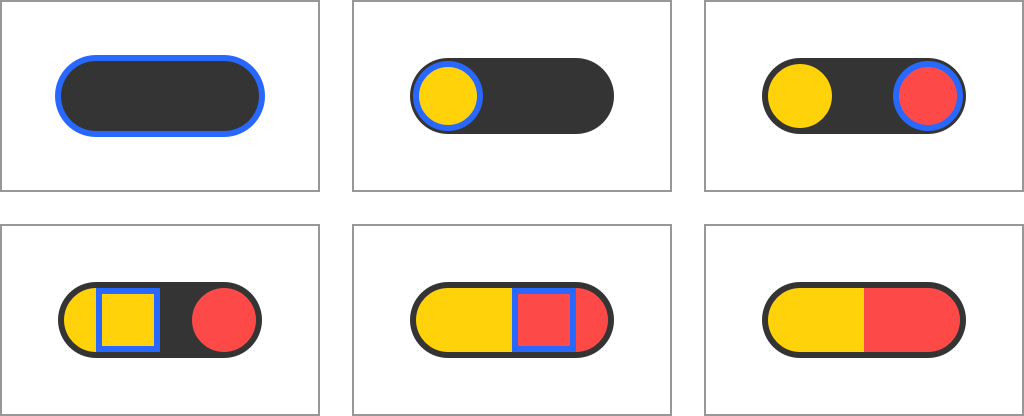
Рисуем пилюлю при помощи простых фигур
Если бы нас попросили отрендерить пилюлю с непрозрачностью 50%, то у нас могло бы возникнуть искушение просто разделить пополам непрозрачность каждой операции отрисовки, но это окажется ошибочным решением:

Неожиданный результат рендеринга пилюли с половинной непрозрачностью
Чтобы достичь правильного результата, мы не можем просто распределить непрозрачность объекта по каждому из его отдельных компонентов. Нам необходимо сначала создать объект, отрендерив его в битовую карту, а уже потом менять непрозрачность битовой карты, и в конце выполнять композитинг:

Ожидаемый результат рендеринга пилюли с половинной непрозрачностью
Это ещё один случай, который демонстрирует полезность концепции рендеринга в побочный буфер.
Покрытие композитингом
Преобразование геометрического покрытия в единственное значение альфы имеет неудобные последствия. Рассмотрим случай, когда в битовую карту рендерятся два идеально совпадающих края фигур векторной геометрии, показанных на рисунке ниже оранжевым и синим контурами. В идеальном мире результаты должны выглядеть приблизительно так, потому то каждый пиксель закрыт полностью:

Идеальный результат рендеринга с правильным покрытием
Однако если мы сначала отрендерим оранжевую геометрию, а затем синюю, то в финальном изображении в пиксели границы всё равно просочится немного белого фона:

Результат двухэтапного композитинга
Как только покрытие сохраняется в альфа-канал, вся его геометрическая информация теряется, и мы никак не можем её восстановить. Синяя геометрия просто смешивается с неким содержимым буфера, но не знает, что геометрия, представленная красноватыми пикселями, должна совпадать с ней. Эта проблема особенно заметна, когда геометрии точно накладываются друг на друга. На рисунке ниже белый круг нарисован поверх чёрного. Заметны тёмные края, хотя оба круга имеют абсолютно одинаковые радиус и позицию:

Белый круг, отрисованный поверх чёрного круга
Один из способов устранения этой проблемы заключается в том, чтобы не вычислять частичное покрытие пикселей, и использовать значительно увеличенные в размерах буферы. Растеризировав векторную геометрию простым покрытием in/out, а затем уменьшив масштаб результата до размеров исходного изображения, можно достичь ожидаемого.
Однако для идеального сопоставления качества рендеринга краёв 8-битного альфа-канала буферы должны быть в 256 раз больше в обоих направлениях, то есть количество пикселей должно увеличиться в 216 раз. Как мы уже видели выше, при снижении битовой глубины для значений покрытия всё равно могут получаться удовлетворительные результаты, поэтому на практике можно использовать и меньший масштаб.
Стоит также заметить, что подобные проблемы часто можно относительно легко избежать без использования огромных битовых карт. Например, вместо отрисовки двух наложенных друг на друга кругов можно просто отрисовать поверх друг друга два квадрата, а затем маскировать результат до формы круга.
Линейные значения
Если вы освежили свои знания о цветовых пространствах, то можете помнить, что большинство из них кодирует цветовые значения нелинейно, и для выполнения правильных математических операций необходима предварительная линеаризация. Когда этот этап выполняется, то результат композитинга выглядит следующим образом; обратите внимание на красивый желтоватый оттенок наложенных друг на друга частей:
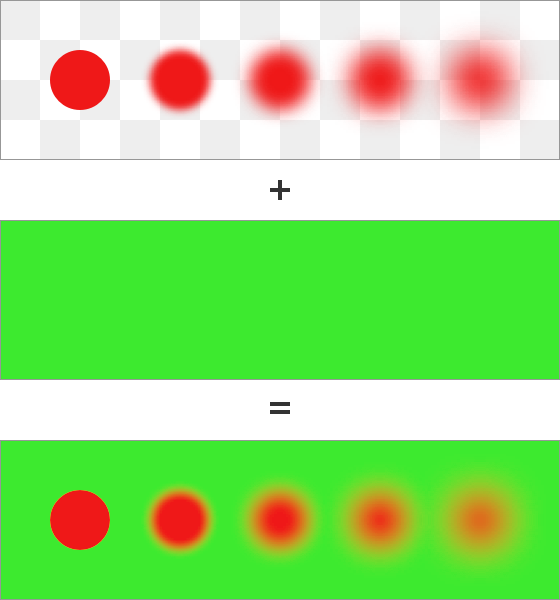
Нечёткие красные круги, наложенные композитингом на зелёный фон при помощи линейных значений
Однако в большинстве случаев композитинг выполняется не так. Стандартным способом для веба и большинства графического ПО является непосредственное смешивание нелинейных значений:

Нечёткие красные круги, наложенные композитингом на зелёный фон при помощи нелинейных значений
Обратите внимание, что области наложения красного на зелёное гораздо темнее. Они далеки от идеала, но в некоторых случаях неправильное выполнение операций глубоко укоренилось в понимании того, как мы воспринимаем цвет. Например, непрозрачный на 50% серый из пространства sRGB выглядит точно так же, как чисто чёрный с непрозрачностью 50%, смешанный с белым фоном:

Композитинг двух цветов на белом фоне без линеаризации
На рисунке ниже цвета sRGB изображений source и destination приведены к линейному виду, а затем преобразованы обратно в нелинейную кодировку для отображения. Вот как должны эти цвета выглядеть на самом деле:

Композитинг двух цветов на белом фоне с линеаризацией
У нас появилось расхождение, не соответствующее нашим ожиданиям. Единственный способ получения визуальной одинаковости при использовании этого метода заключается в подборе всех цветов при помощи линейных значений, но это сильно отличается от того, к чему все привыкли. Серый на 50% с линейными значениями выглядит как серый на 73.5% пространства sRGB.
Кроме того, нужно быть особенно внимательными при работе с premultiplied alpha. Предварительное умножение должно выполняться с линейными значениями, т.е. до кодирования в нелинейные. Благодаря этому этап линеаризации верно завершится с правильными линейными значениями, предварительно умноженными на альфу.
Premultiplied Alpha и битовая глубина
Несмотря на свою большую полезность для композитинга, фильтрации и интерполяции, premultiplied alpha не является «серебряной пулей» и имеет свои недостатки. Самый серьёзный из них — снижение битовой глубины цветов, которые можно представить. Представим 8-битное кодирование значения 150, которое предварительно умножается на альфу 20%. После предварительного умножения на альфу мы получаем
round(150 × 0.2) = 30
Если мы повторим ту же процедуру со значением 151, то получим:
round(151 × 0.2) = 30
Закодированное значение будет таким же, несмотря на различие исходных значений. На самом деле, после умножения на альфу значения 148, 149, 150, 151 и 152 кодируются в 30, и исходное различие между этими пятью уникальными цветами теряется:

Предварительное умножение на альфу 20% сводит различные 8-битные значения к одному
Естественно, чем меньше альфа, тем разрушительнее её влияние. Из возможного диапазона в 2564 (примерно 4,3 миллиарда) различных комбинаций 8-битных значений RGBA после предварительного умножения на альфу сохраняют уникальное представление только 25.2%; по сути, мы теряем почти 2 бита из 32-битного диапазона.
Для преобразования цветов между различными цветовыми пространствами иногда необходимо обратить предварительное умножение, то есть разделить значения на компонент альфы, чтобы получить исходную яркость цвета. Этот этап обязателен, потому что, как говорилось выше, кодирование выполняется нелинейно. Существование предварительного умножения снижает точность представления цвета и преобразования между цветовыми пространствами могут быть неидеальными.
На практике снижение битовой глубины редко оказывается важным, особенно в композитинге. Чем ниже значение альфы, тем менее видим цвет, и тем меньшее влияние он оказывает на композитинг. В конечном итоге, если вы стремитесь к педантично точным операциям над цветами, вы не будете использовать их 8-битное представление — для такой цели гораздо лучше подходят форматы с плавающей запятой.
Дополнительное чтение
Концепция альфа-канала была создана сооснователями студии Pixar Элви Смитом и Эдом Кэтмеллом. В статье Смита “Alpha and the History of Digital Compositing” описывается история изобретения и источники названия “alpha”, а также рассказывается о том, как эти концепции развивались и постепенно заменили в кинопроизводстве концепцию маски.
Для понимания значения альфы я крайне рекомендую вам прочитать статью Эндрю Гласснера “Interpreting Alpha”. В этой статье приводится строгий, но очень доступный математический вывод альфы как меры взаимодействия между непрозрачностью и покрытием.
Подробное рассмотрение premultiplied alpha можно изучить в “GPUs prefer premultiplication” Эрика Хейнса. В статье не только приведён отличный обзор проблем, вызываемых отсутствием предварительного умножения, особенно в 3D-рендеринге, но и представлены ссылки на множество других статей по этой теме.
В заключение
Изначально эта статья задумывалась как объяснение операторов композитинга Портера-Даффа, но все остальные концепции, связанные с альфа-композитингом, оказались настолько интересными, что я не мог их пропустить.
В альфе мне больше всего нравится то, что это просто дополнительное число, сопровождающее RGB-компоненты, но в то же время оно создаёт множество уникальных возможностей в рендеринге. Альфа в буквальном смысле создала новое изменение возможностей в скучном старом мире композитинга и 2D-рендеринга.
Когда в следующий раз вы увидите гладкие края векторных фигур или заметите тёмный оверлей, затемняющий некоторые части интерфейса пользователя, вспомните о небольшом, но мощном компоненте, благодаря которому всё это стало возможным.
Автор: PatientZero






