Полный курс на русском языке можно найти по этой ссылке.
Оригинальный курс на английском доступен по этой ссылке.

Выход новых лекций запланирован каждые 2-3 дня.

Содержание

1. Интервью с Себастьяном Труном
2. Введение
3. Набор данных собак и кошек
4. Изображения различного размера
5. Цветные изображения. Часть 1
6. Цветные изображения. Часть 2
7. Операция свёртки на цветных изображениях
8. Операция подвыборки по максимальному значению на цветных изображениях
9. CoLab: кошки и собаки
10. Softmax и sigmoid
11. Проверка
12. Расширение изображений
13. Исключение
14. CoLab: собаки и кошки. Повторение
15. Другие техники для предотвращения переобучения
16. Упражнения: классификация изображений цветов
17. Решение: классификация изображений цветов
18. Итоги

Интервью с Себастьяном Труном

— Итак, сегодня мы снова здесь, вместе с Себастьяном и говорить мы будем о переобучении. Эта тема нам очень интересна, особенно в практических частях текущего курса по работе с TensorFlow.
— Себастьян, сталкивались ли вы когда-то с переобучением (overfitting — over, fit)? Если вы скажете, что не сталкивались, то я определённо скажу, что не могу вам верить!
— Итак, причиной переобучения является так называемый bias-variance trade-off (компромисс между значениями параметра смещения и их разбросом). Нейронная сеть у которой малое количество весов не способна выучить достаточное количество примеров, подобная ситуация в машинном обучении называется искажением.
— Да.
— Нейронная сеть у которой очень много параметров может произвольным образом выбрать решение, которое вам не понравится, как раз из-за такого большого количества этих параметров. Результат выбора решения нейронной сети зависит от вариантивности исходных данных. Таким образом можно сформулировать простое правило: чем больше параметров присутствует в сети относительно размеров (количества) данных, тем больше вероятность получить случайное решение вместо нужного верного. Например, вы задётесь вопросом "Кто в этой комнате мужчина, а кто — женщина?". Сложная нейронная сеть может сообщить вам, что, например, все те у кого имена начинаются на Т — мужчины и, никогда не переобучиться. Существует два решения. Первое из них использует holdout-набор данных (небольшое количество из обучающей выборки для валидации точности работы модели). Вы можете взять данные, разделить их на две части — 90% на обучение, а 10% на тестирование и провести так называемую кросс-валидацию, где вы проверите точность работы модели на тех данных, которые нейронная сеть не видела — как только значение ошибки начнет расти после определенного цикла обучения,- пора останавливать обучение. Второе решение заключается в том, чтобы ввести в нейронную сеть ограничения. Например, ограничить значения параметров смещений и весов, приводя их всё ближе и ближе к нулю. Чем более ограничены веса, тем менее переобученной будет модель.
— Я правильно понимаю, что у нас могут быть наборы данных как для обучения, так и для тестирования и валидации, верно?
— Верно. Если у вас есть набор данных для валидации, то у вас должен быть такой набор данных, к которому вы ещё никогда не притрагивались и не показывали его вашей нейронной сети. Если же вы показывали модели определённый набор данных много раз, то, безусловно, начнется процесс переобучения, что очень плохо для нас.
— Может быть вы вспомните наиболее интересные случаи, когда ваша модель переобучалась?
— Ах, да… был такой случай в далёкой молодости, когда я занимался разработкой нейронной сети для игры в шахматы. Это было в 1993. Что интересно было, так это то, что из шахматных данных на которых обучалась нейронная сеть, сеть быстро определила, что если эксперт делает ход королевой в центр шахматной доски, то существует 60% вероятность победы. Что она начала делать — открывать "проход" пешкой и двигать королеву в центр шахматной доски. Это было настолько глупым решением для любого игрока в шахматы, которое явно свидетельствовало о переобученности модели.
— Здорово! Итак, мы обсудили несколько техник относительно того, как можно улучшить наши модели. Как вы думаете, что является наиболее недооценённой стороной глубокого обучения?
— 90% вашей работы недооценены, потому что 90% вашей работы будет состоять в очистке данных.
— Здесь я с вами полностью согласна!
— Как показывает практика, любой набор данных содержит какой-то мусор. Привести данные к нужному виду, сделать их консистентными очень сложно, это очень трудоёмкий процесс.
— Да, даже если ты работаешь с такими наборами данных как изображения или видео, где, казалось бы, вся информация уже там, внутри, всё равно есть необходимость производить предобработку изображений.
— Единственные люди для которых данные идеальны — это профессора, потому что у них есть возможность сделать вид в презентации в PowerPoint, что всё именно так и должно быть и всё идеально! В реальности же 90% вашего времени будет занимать очистка данных.
— Отлично. Итак, давайте узнаем больше о переобучении и техниках, которые позволят нам усовершенствовать наши модели глубокого обучения.

Введение

— Привет! И снова добро пожаловать на курс!
— На прошлом уроке мы разработали небольшую свёрточную нейронную сеть для классификации изображений элементов одежды в оттенках серого цвета из набора данных FASHION MNIST. Мы убедились на практике в том, что наша небольшая нейронная сеть может классифицировать поступающие на вход изображения с достаточно высокой точностью. Однако в реальном мире нам предстоит работать с изображениями высокого разрешения и различных размеров. Одним из замечательных преимуществ СНС является тот факт, что они могут так же хорошо работать и с цветными изображениями. Поэтому мы начнём наш текущий урок с изучиния того, каким образом СНС работает с цветными изображениями.
— Позже, в этой же часты, вы построите свёрточную нейронную сеть, которая сможет классифицировать изображения кошек и собак. На пути к реализации свёрточной нейронной сети способной классифицировать изображения кошек и собак, мы так же научимся использовать различные техники для решения одной и самых частых проблем с нейронными сетями — переобучении. А в конце этого урока, в практической части, вы разработаете собственную свёрточную нейронную сеть для классификации изображений цветов. Давайте начинать!

Набор данных кошек и собак

До этого момента мы работали только с изображениями в оттенках серого цвета и размером 28х28 из набора данных FASHION MNIST.

В реальных же приложениях мы вынуждены сталкиваться с изображениями различного размера, например, такими, которые показаны ниже:

Как мы уже упоминали в начале этого урока, на этом занятии мы будем разрабатывать свёрточную нейронную сеть, которая сможет классифицировать цветные изображения собак и кошек.

Для реализации задуманного мы воспользуемся изображениями кошек и собак из набора данных Microsoft Asirra. Каждое изображение в этом наборе данных обладает меткой 1 или 0, если на изображении, соответственно, собака или кошка.

Несмотря на то, что набор данных Microsoft Asirra содержит более 3 млн размеченных изображений кошек и собак, лишь 25 000 доступы публично. Тренировка нашей свёрточной нейронной сети на этих 25 000 изображениях займёт очень много времени. Именно поэтому мы будем использовать небольшое множество изображений для тренировки нашей свёрточной нейронной сети из доступных 25 000.

Наше подмножество тренировочных изображений состоит из 2 000 шт и 1 000 шт изображений для валидации модели. В тренировочном наборе данных 1 000 изображений содержит кошек, а другая 1 000 изображений — собак. О наборе данных для валидации мы поговорим немного позже в этой части урока.

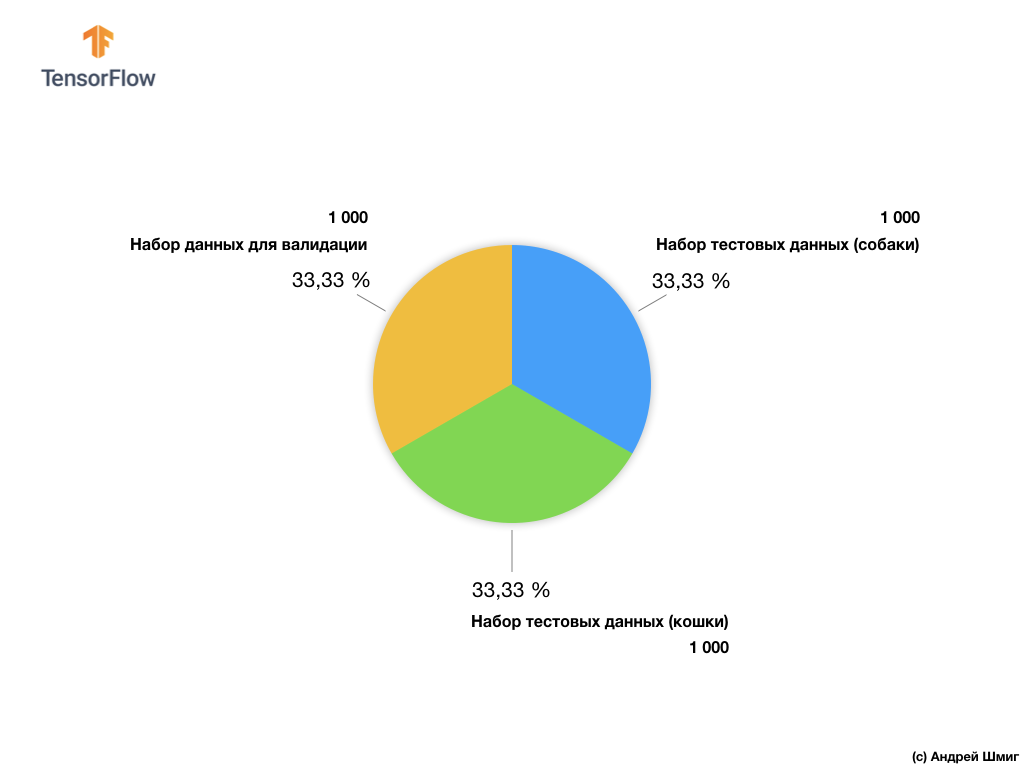
Работая с данным набором данных мы столкнёмся с двумя основными трудностями — работа с изображениями разного размера и работа с цветными изображениями.

Давайте начнём изучение того, каким образом необходимо работать с изображениями различных размеров.

Изображения различного размера

Наше первое испытание будет заключаться в решении задачи обработки изображений различного размера. Всё потому, что нейронной сети на вход нужны фиксированного размера данные.

В качестве примера вы можете вспомнить из наших предыдущих частей использование input_shape параметра при создании Flatten-слоя:

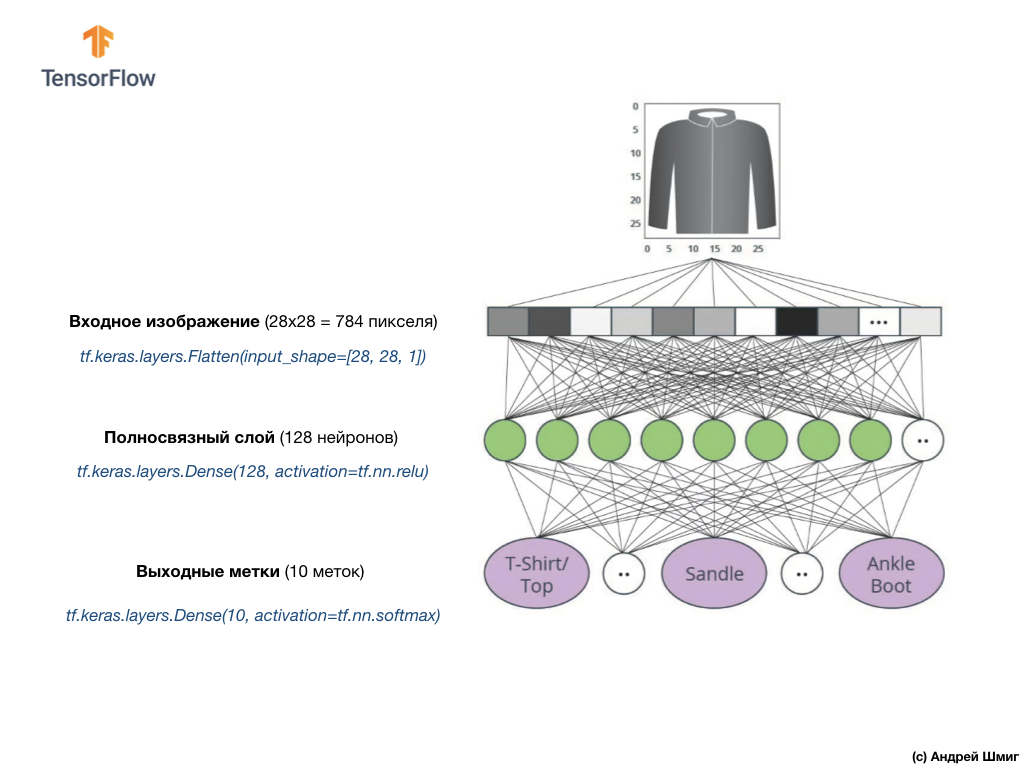
Перед тем как передавать нейронной сети изображение элемента одежды мы его преобразовывали в 1D-массив фиксированного размера — 28х28 = 784 элемента (пикселя). Так как изображения в наборе данных Fashion MNIST были одного размера, то и результатирующий одномерный массив был одного размера и состоял из 784 элементов.

Однако, работая с изображениями различного размера (высота и ширина) и преобразовывая их в одномерные массивы мы получим массивы различных размеров.

Так как нейронные сети на входе требуют данных одного размера, то просто отделаться преобразованием к одномерному массиву значений пикселей уже не сработает.

Решая задачи классификации изображений мы всегда прибегаем к одному из вариантов унификации входных данных — приведение размеров изображений к единым значениям (resizing).

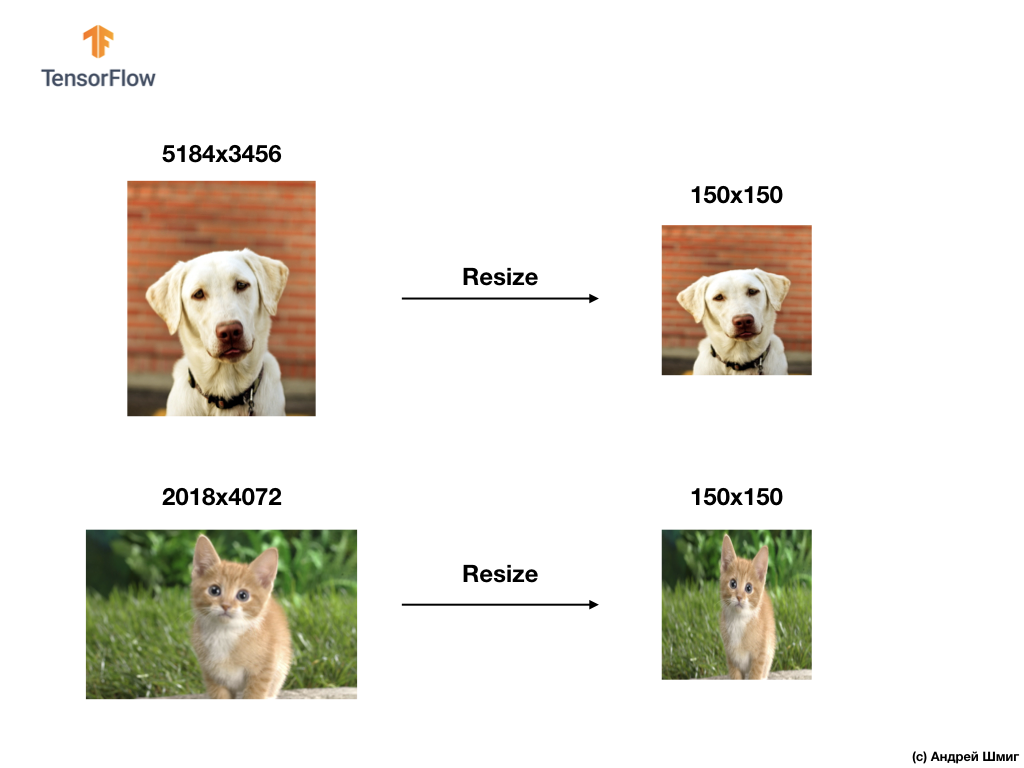
В этом уроке мы прибегнем к изменению размеров всех изображений к размерам 150 пикселей по высоте и 150 пикселей по ширине. Преобразовывая изображения к единому размеры мы, тем самым, гарантируем, что на вход нейронной сети будет поступать картинка нужного размера и при передаче во flatten-слой мы получим одномерный массив такого же размера.

tf.keras.layers.Flatten(input_shape(150,150,1))

В результате мы получил одномерный массив состоящий из 150х150 = 22 500 значений (пикселей).

Следующей проблемой с которой нам предстоит столкнуться будет проблема цвета — цветные изображения. О них мы поговорим в следующей части.

Цветные изображения. Часть 1

Для того чтобы разобраться и понять, каким образом свёрточные нейронные сети работают с цветными изображениями нам стоит углубиться в то, как именно СНС работают вообще. Давайте освежим в памяти то, что мы уже знаем.

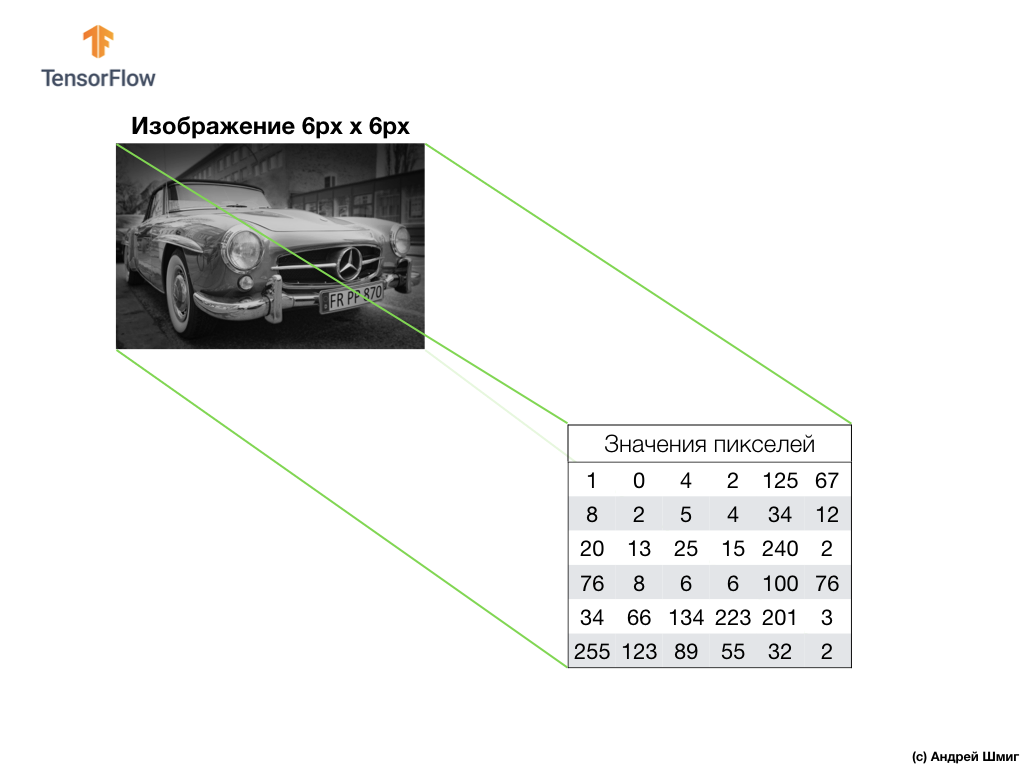
Пример выше — изображение в оттенках серого цвета и то, каким образом его интерпретирует компьютер в виде двумерного массива значений пикселей.

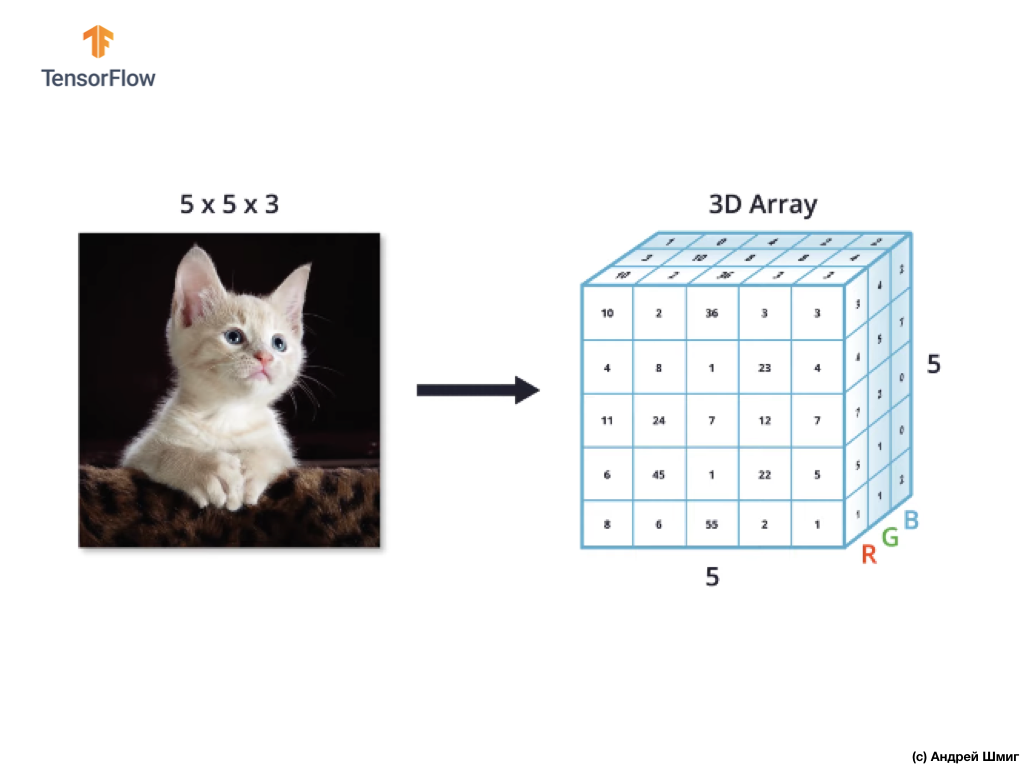
Пример ниже — изображение, на этот раз цветное и то, каким образом его интерпретирует компьютер в виде трёхмерного массива значений пикселей.

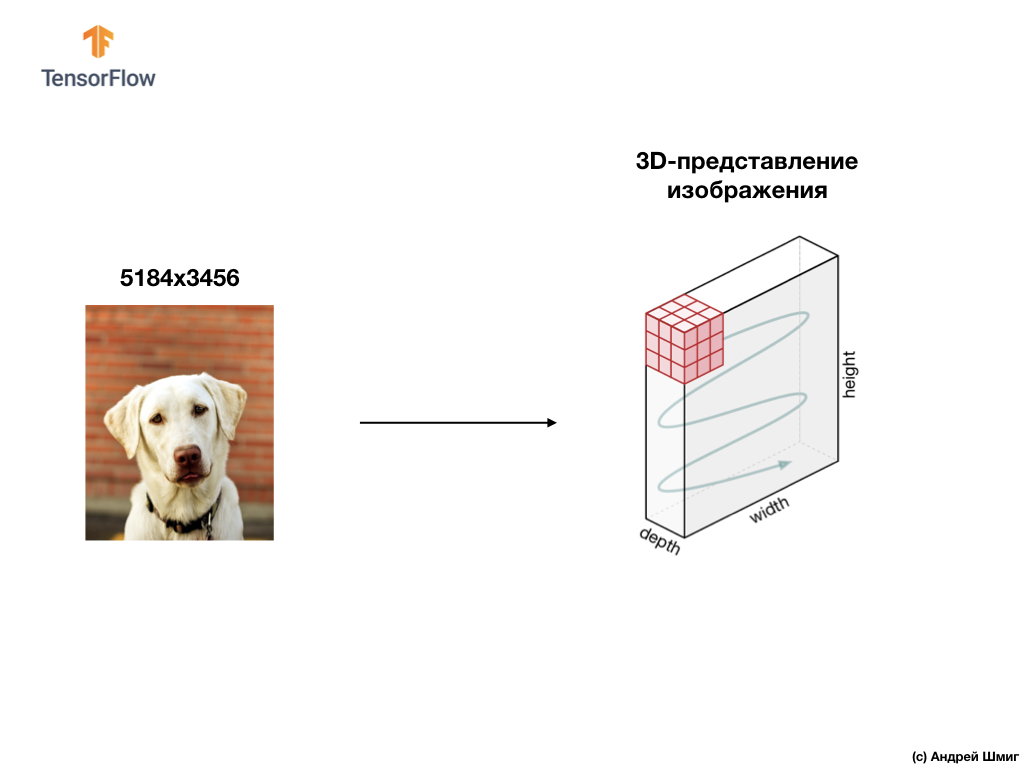
Высота и ширина 3D-массива будет определена высотой и шириной изображения, а глубина (depth) определяет количеством цветовых каналов изображения.

Большинство цветных изображений могут быть представлены тремя цветовыми каналами — красным (red), зеленым (green) и синим (blue).

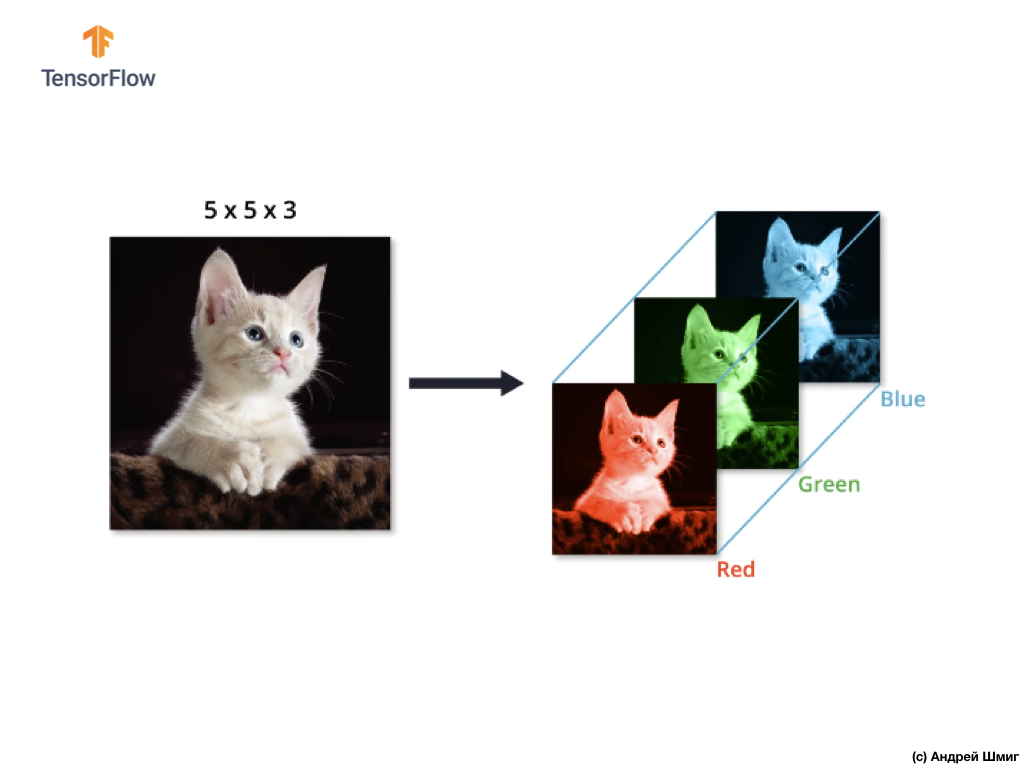
Изображения, которые состоят из красного, зеленого и синего каналов называются RGB-изображениями. Объединение этих трёх каналов в результате даёт цветное изображение. В каждом из RGB-изображении, каждый канал представлен отдельным двумерных массивом пикселей.

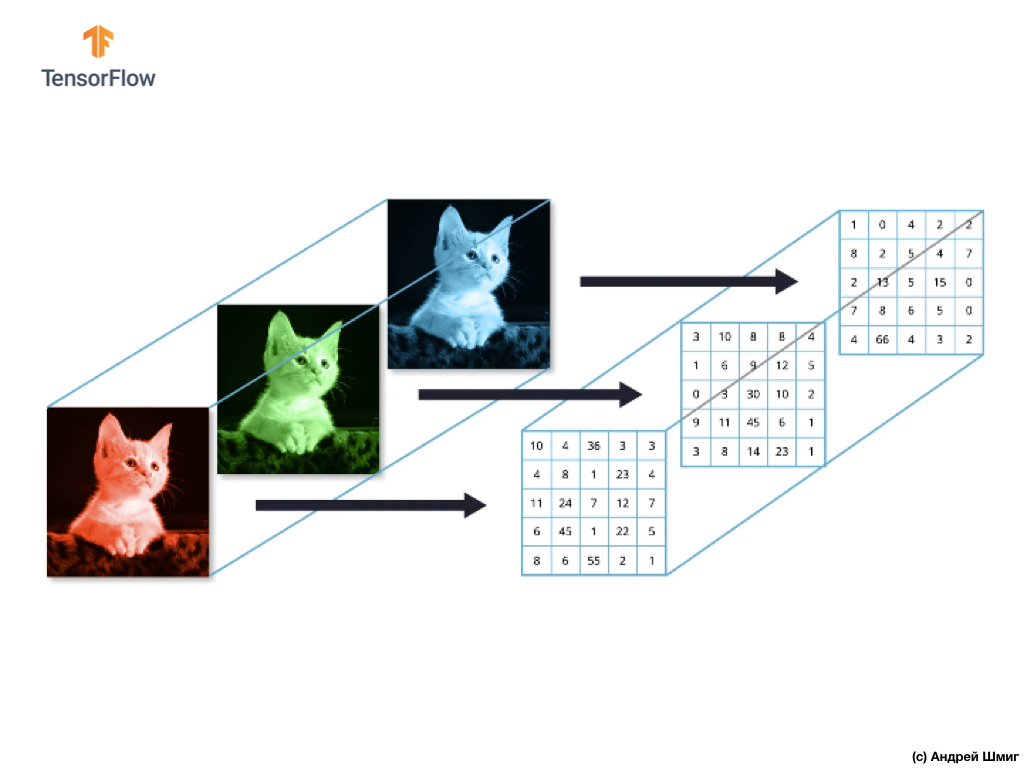
Так как количество каналов у нас равно трём, то и в результате у нас будут три двумерных массива. Таким образом цветное изображение состоящее из 3 цветовых каналов будет иметь следующее представление:

Цветные изображения. Часть 2

Итак, так как наше изображение теперь будет состоять из 3 цветов, а значит будет представлять собой трёхмерный массив значений пикселей, то и наш код необходимо будет изменить соответствующим образом.

Если посмотреть на код, который мы использовали в нашем прошлом уроке, когда решали задачу классификации элементов одежды на изображениях, то можно заметить, что мы указывали размерность входных данных:

model = Sequential()
model.add(Conv2D(32, 3, padding='same', activation='relu', input_shape=(28,28,1)))

Первые два параметра кортежа (28,28,1) являются значениями высоты и ширины изображения. Изображения в наборе данных Fashion MNIST были размером 28х28 пикселей. Последней параметр в кортеже (28,28,1) обозначает количество каналов цветов. В наборе данных Fashion MNIST изображения были только в оттенках серого — 1 цветовой канал.

Теперь, когда задача стала чуточку сложнее, а наши изображения кошек и собак стали различного размера (но преобразуются к единому — 150х150 пикселей) и содержат 3 цветовых канала, то кортеж значений должен быть тоже другим:

model = Sequential()
model.add(Conv2D(16, 3, padding='same', activation='relu', input_shape=(150,150,3)))

В следующей части мы посмотрим, каким образом происходит вычисление свёртки при наличии трёх цветовых каналов в изображении.

Операция свёртки на цветных изображениях

В прошлых уроках мы научились выполнять операцию свёртки на изображениях в оттенках серого. Но каким образом выполнять операцию свёртки на цветных изображениях? Давайте начнём с повторения, каким образом выполняется операция свёртки на изображениях в оттенках серого.

Всё начинается с фильтра (ядра) определённого размера.

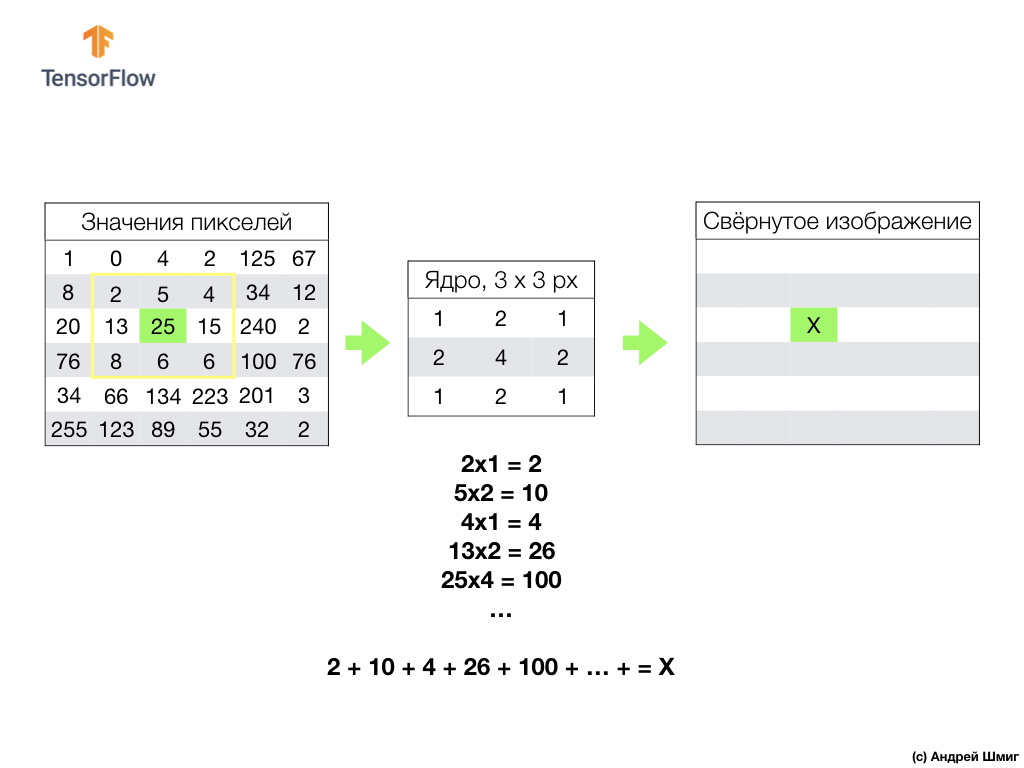
Фильтр располагается на определенным преобразуемым пикселем изображения, затем каждое значения фильтра умножается на подлежащее значение пикселя в изображении и все эти значения суммируются. Итоговое значение пикселя устанавливается в новом изображении в том месте, где находился преобразованный исходный пиксель. Операция повторяется для каждого пикселя исходного изображения.

Стоит так же вспомнить, что при операции свёртки, дабы не терять информацию на границах изображения, мы можем применить выравнивание и дополнить края изображения нулями:

Теперь давайте разберёмся, каким образом мы можем выполнить операцию свёртки над цветными изображениями.

Так же, как и при преобразовании изображения в оттенках серого, начнем мы с выбора размера фильтра (ядра) определённого размера.

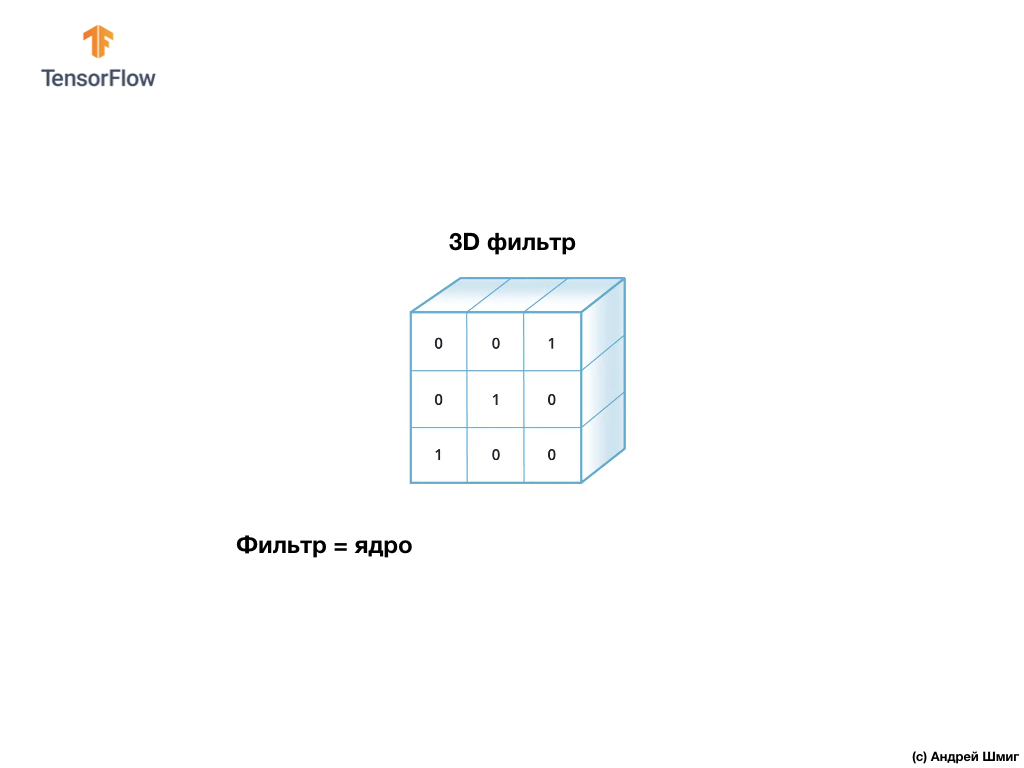
Единственная разница сейчас будет в том, что теперь и сам фильтр будет трёхмерным, а значение параметра глубины (depth) будет равно значению количества цветовых каналов в изображении — 3 (в нашем случае — RGB). К каждому "слою" цветового канала мы так же будем применять операцию свёртки фильтром выбранного размера. Давайте посмотрим, как это будет на примере.

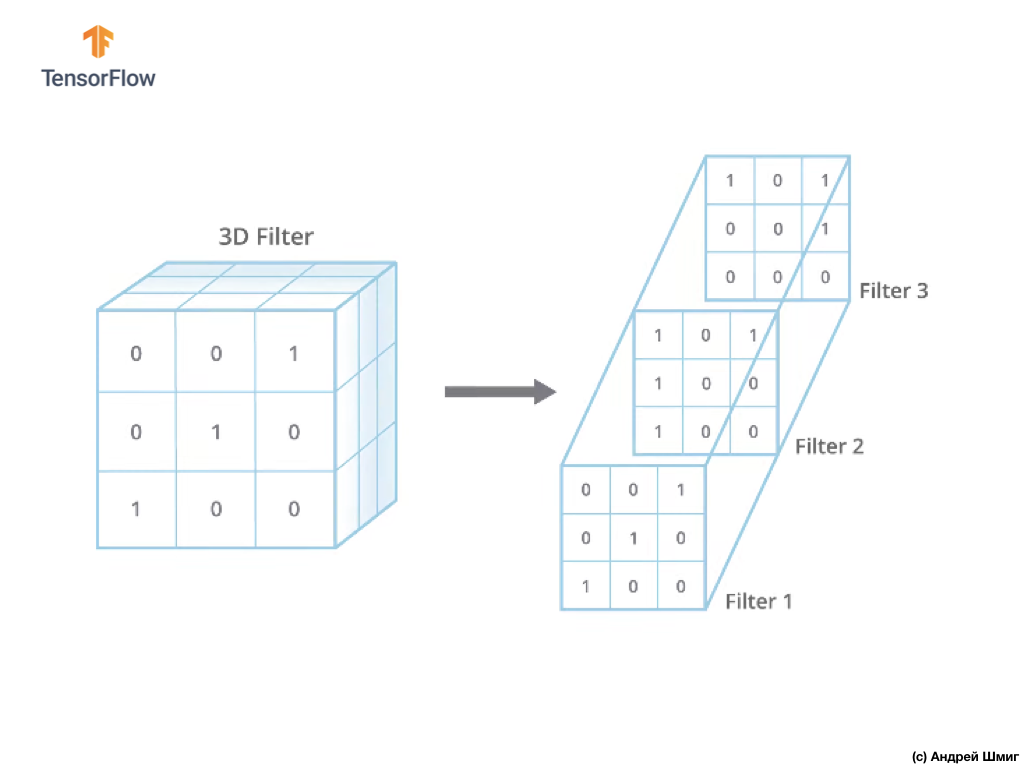
Представьте, что у нас есть RGB-изображение и мы хотим применить операцию свёртки следующим 3D-фильтром. Стоит обратить внимание на тот факт, что наш фильтр состоит из 3х двумерных фильтров. Для простоты давайте представим, что наше RGB-изображение размером 5х5 пикселей.

Вспомним так же, что каждый цветовой канал представляет собой двумерный массив значений цветов пикселей.

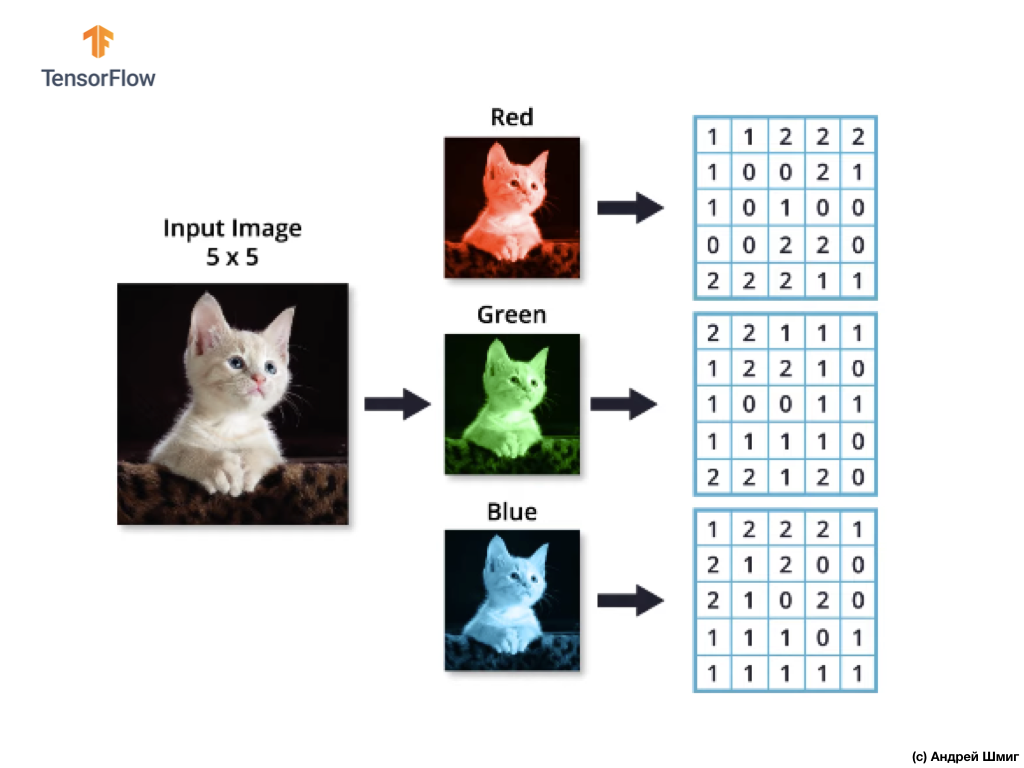
Как и при выполнении операции свёртки над изображениями в оттенках серого, так же и с цветными изображениями — осуществим выравнивание и дополним изображение по краям нулями, чтобы исключить потерю информации на границах.

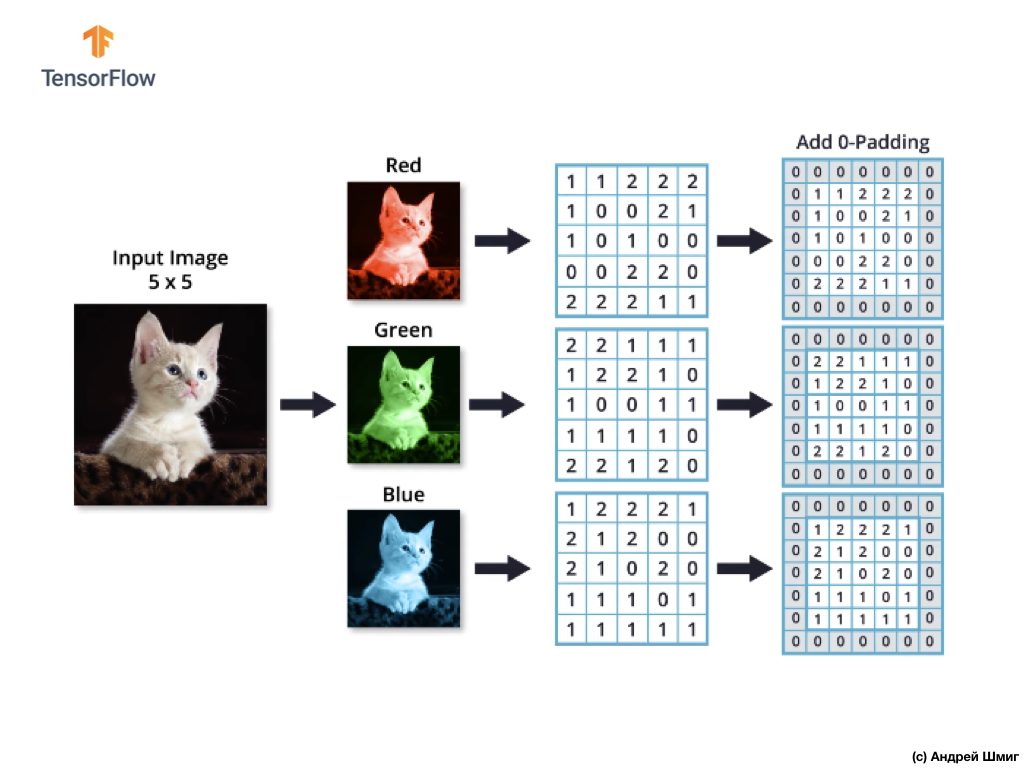
Теперь мы готовы к выполнению операции свёртки!

Механизм выполнения свёртки для цветных изображений будет аналогичным процессу, который мы выполняли с изображениями в оттенках серого. Единственная разница между выполняемыми операциями над изображениями в оттенках серого и цветными — операцию свёртки теперь необходимо выполнить 3 раза по каждому цветовому каналу.

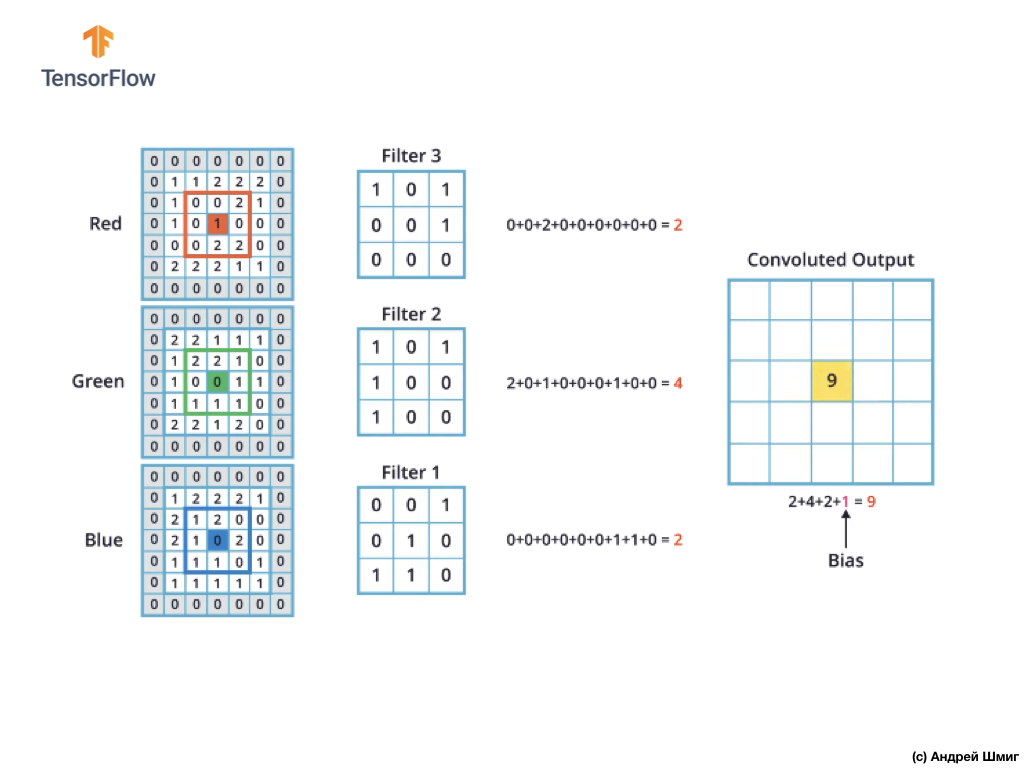
Затем, после того как мы выполнили операцию свёртки над каждым цветовым каналом — складываем три полученных значения и прибавляем к ним 1 (стандартное значение используемое при выполнении операций подобного рода). Полученное новое значение фиксируем в той же позиции в новом изображении, в какой позиции находился текущий преобразуемый пиксель.

Подобную операцию преобразования (операцию свёртки) мы выполняем для каждого пикселя в нашем исходном изображении и по каждому цветовому каналу.

В этом конкретном примере результатирующее изображение получилось такого же размера по высоте и ширине, как и наше исходное RGB-изображение.

Как можно заметить, применение операции свёртки единственным 3D-фильтром даёт в результате единственное выходное значение.

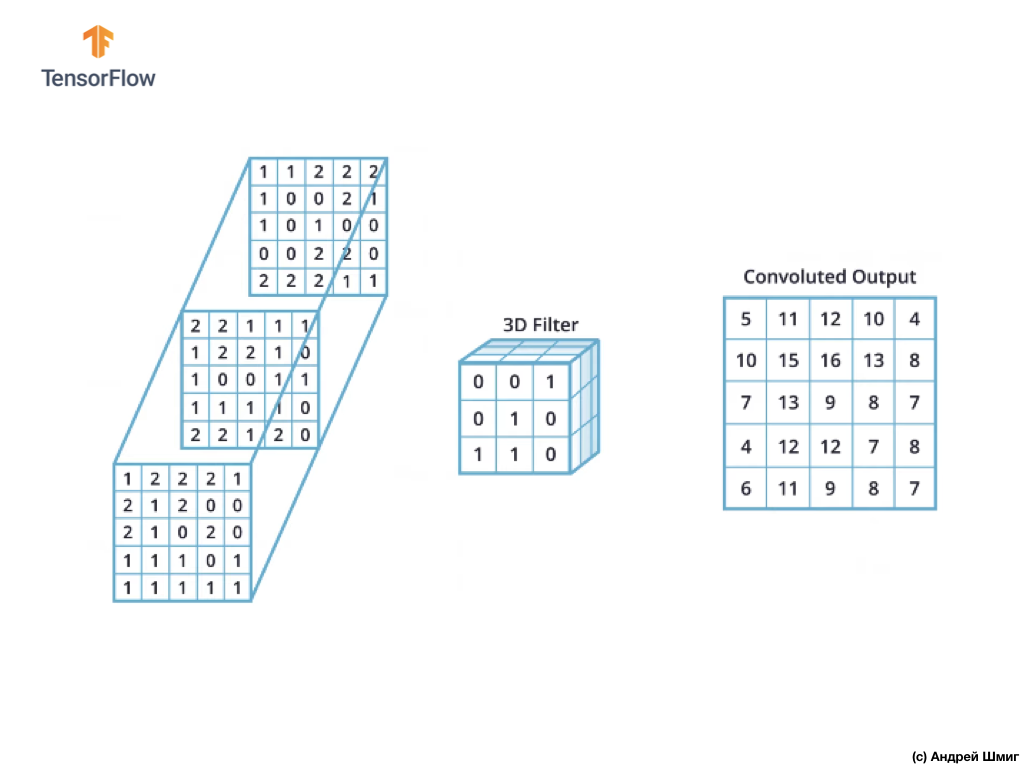
Однако, когда работа ведётся со свёрточными нейронными сетями, обычной практикой считается использование более одного 3D-фильтра. Если мы будем использовать более одного 3D-фильтра, то результатом будет несколько выходных значений — каждое значение на результат работы одного фильтра.

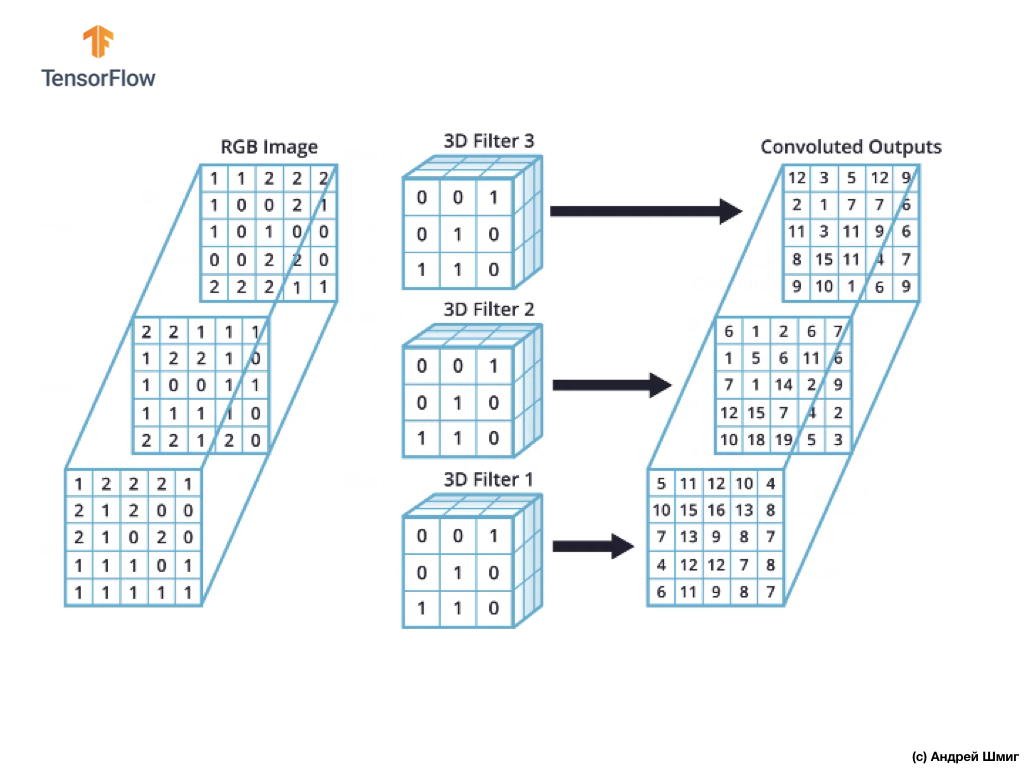
В нашем примере выше, так как мы используем 3 фильтра, то результатирующее 3D-представление будет иметь глубину 3 — каждый слой будет соответствовать выходному значению преобразования одного фильтра над изображением со всеми его цветовыми каналами.

Если, например, вместо 3 фильтров мы решили бы использовать 16, то выходное 3D-представление содержало бы 16 глубинных слоёв.

В коде мы можем контролировать количество создаваемых фильтров передавая соответствующее значение для параметра filters:

tf.keras.layers.Conv2D(filters, kernel_size, ...)

Так же мы можем указывать размер фильтра через параметр kernel_size. Например, для создания 3 фильтров размером 3х3, как было в нашем примере выше, мы можем записать код следующим образом:

tf.keras.layers.Conv2D(3, (3,3), ...)

Запомните, что во время тренировки свёрточной нейронной сети, значения в 3D-фильтрах будут обновляться, чтобы минимизировать значение функции потерь.

Теперь, когда мы знаем как выполнять операцию свёртки на цветных изображениях, пора разобраться с тем, как к полученному результату применять операцию подвыборки по максимальному значению (тот самый max-pooling).

Операция подвыборки по максимальному значению на цветных изображениях

Давайте теперь научимся выполнять операцию подвыборки по максимальному значению на цветных изображениях. По сути, операция подвыборки по максимальному значению работает таким же образом, как работает с изображениями в оттенках серого с небольшой лишь разницей — операцию подвыборки теперь необходимо применить к каждому выходному представлению, которые мы получили в результате применения фильтров. Давайте посмотрим на пример.

Для простоты давайте представим, что наше выходное представление выглядит таким образом:

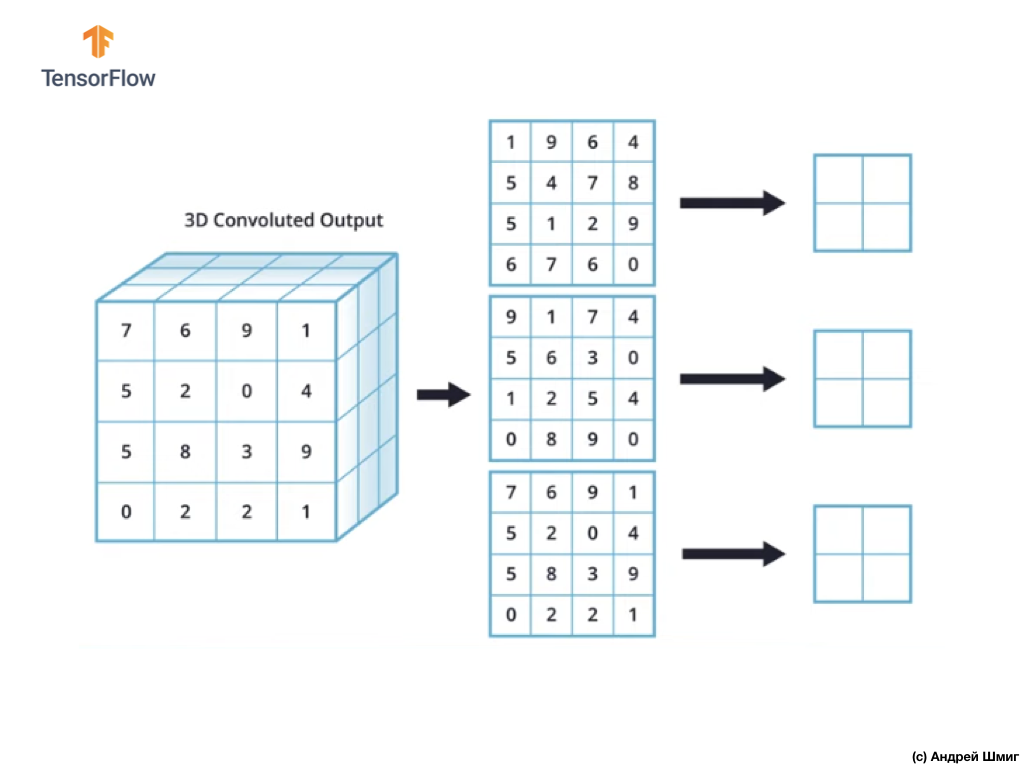
Как и ранее, мы будем использовать ядро размером 2х2 и шагом 2 для выполнения операции подвыборки по максимальному значению. Операция подвыборки по максимальному значению начинается с "установки" ядра размером 2х2 в левом верхнем углу каждого выходного представления (представления, которое было получено после применения операции свёртки).

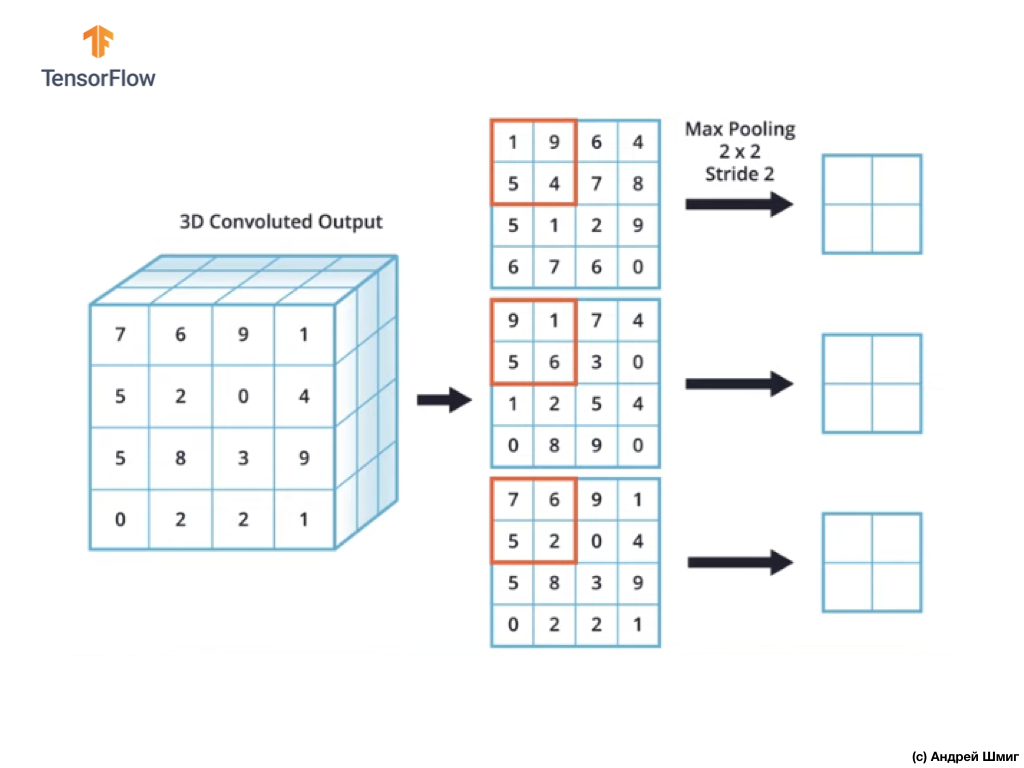
Теперь мы можем начать выполнять операцию подвыборки по максимальному значению. Например, в нашем первом выходном представлении в ядро размером 2х2 попали следующие значения — 1, 9, 5, 4. Так как максимальное значение в этом ядре — 9, то именно она и отправляется в новое выходное представление. Подобная операция повторяется для каждого входного представления.

В итоге мы должны получить следующий результат:

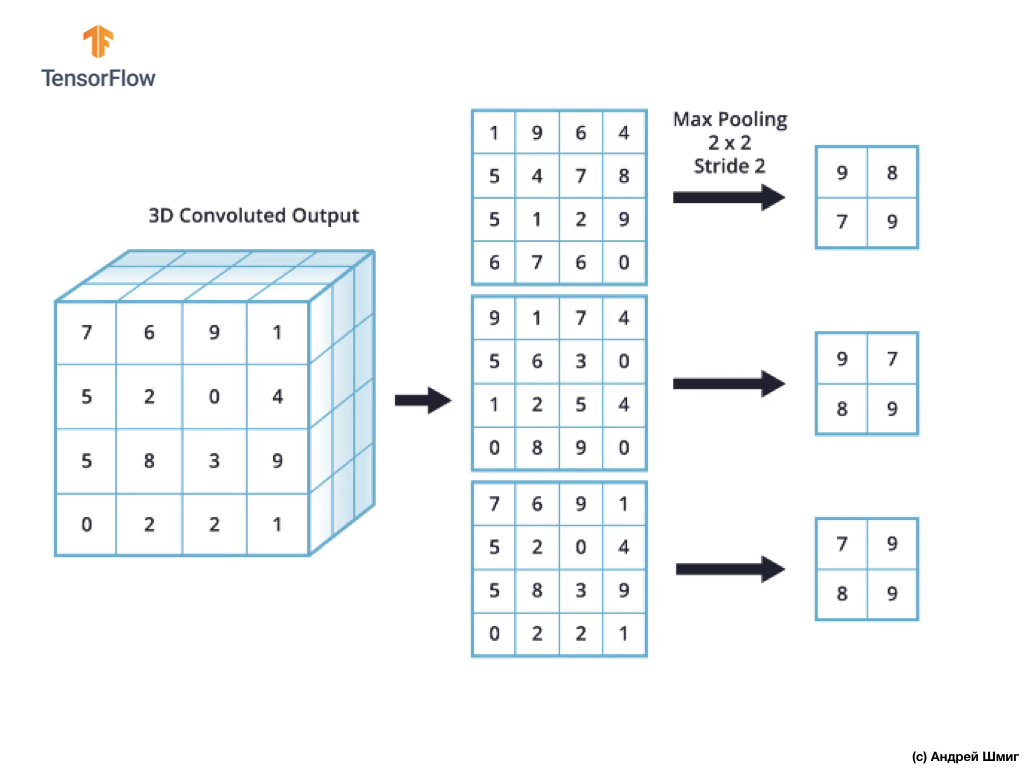
После выполнения операции подвыборки по максимальному значению в результате получаются 3 двумерных массива, каждый из которых размером в 2 раза меньше исходного входного представления.

Таким образом, в этом конкретном случае, при выполнении операции подвыборки по максимальному значению над трёхмерным входным представлением мы получаем в результате трёхмерное выходное представление той же глубины, но со значениями высоты и ширины в два раза меньше исходных значений.

Итак, это вся теория, которая нам понадобится для дальнейшей работы. Теперь давайте посмотрим, как же это будет работать в коде!

CoLab: кошки и собаки

Оригинальный CoLab на английском языке доступен по этой ссылке.
CoLab на русском языке доступен по этой ссылке.

В этой обучающей части мы обсудим то, каким образом можно классифицировать изображения кошек и собак. Мы разработаем классификатор изображений с использованием tf.keras.Sequential-модели, а для загрузки данных воспользуемся tf.keras.preprocessing.image.ImageDataGenerator.

Идеи, которые будут затронуты в этой части:

Мы получим практический опыт разработки классификатора и разовьём интуитивное понимание следующих концепций:

1. Построение модели потока данных (data input pipelines) с использованием tf.keras.preprocessing.image.ImageDataGenerator-класса (Каким образом эффективно работать с данными на диске взаимодействуя с моделью?)
2. Переобучение — что это такое и как его определить?

Перед тем как мы начнем...

Перед тем как запускать код в редакторе, рекомедуем сбросить все настройки в Runtime -> Reset all в верхнем меню. Подобное действие позволит избежать проблем с нехваткой памяти, если параллельно вы работали или работаете с несколькими редакторами.

Импортирование пакетов

Давайте начнём с импорта нужных пакетов:

• os — чтение файлов и структуры директорий;
• numpy — для некоторых матричных операций вне TensorFlow;
• matplotlib.pyplot — построение графиков и отображение изображений из тестового и валидационного набора данных.

from __future__ import absolute_import, division, print_function, unicode_literals

import os
import matplotlib.pyplot as plt
import numpy as np

Импортируем TensorFlow:

import tensorflow as tf
from tensorflow.keras.preprocessing.image import ImageDataGenerator

import logging
logger = tf.get_logger()
logger.setLevel(logging.ERROR)

Загрузка данных

Разработку нашего классификатора мы начинаем с загрузки набора данных. Набор данных, который мы используем представляет собой отфильтрованную версию набора данных Собаки vs Кошки с сервиса Kaggle (в конце концов именно этот набор данных предоставляется Microsoft Research).

В прошлом CoLab мы с вами использовали набор данных из самого TensorFlow Dataset модуля, который оказывается крайне удобным для работы и тестирования. В этом CoLab однако, мы воспользуемся классом tf.keras.preprocessing.image.ImageDataGenerator для чтения данных с диска. Поэтому предварительно нам необходимо загрузить набор данных Собаки VS Кошки и разархивировать его.

_URL = 'https://storage.googleapis.com/mledu-datasets/cats_and_dogs_filtered.zip'
zip_dir = tf.keras.utils.get_file('cats_and_dogs_filterted.zip', origin=_URL, extract=True)

Набор данных, который мы загрузили, имеет следующую структуру:

cats_and_dogs_filtered
|__ train
    |______ cats: [cat.0.jpg, cat.1.jpg, cat.2.jpg ...]
    |______ dogs: [dog.0.jpg, dog.1.jpg, dog.2.jpg ...]
|__ validation
    |______ cats: [cat.2000.jpg, cat.2001.jpg, cat.2002.jpg ...]
    |______ dogs: [dog.2000.jpg, dog.2001.jpg, dog.2002.jpg ...]

Чтобы получить полный список директорий можно воспользоваться следующей командой:

zip_dir_base = os.path.dirname(zip_dir)
!find $zip_dir_base -type d -print

В результате получим нечто подобное:

/root/.keras/datasets
/root/.keras/datasets/cats_and_dogs_filtered
/root/.keras/datasets/cats_and_dogs_filtered/train
/root/.keras/datasets/cats_and_dogs_filtered/train/dogs
/root/.keras/datasets/cats_and_dogs_filtered/train/cats
/root/.keras/datasets/cats_and_dogs_filtered/validation
/root/.keras/datasets/cats_and_dogs_filtered/validation/dogs
/root/.keras/datasets/cats_and_dogs_filtered/validation/cats

Теперь присвоим переменным корректные пути к директориям с наборами данных для тренировки и валидации:

base_dir = os.path.join(os.path.dirname(zip_dir), 'cats_and_dogs_filtered')
train_dir = os.path.join(base_dir, 'train')
validation_dir = os.path.join(base_dir, 'validation')

train_cats_dir = os.path.join(train_dir, 'cats')
train_dogs_dir = os.path.join(train_dir, 'dogs')
validation_cats_dir = os.path.join(validation_dir, 'cats')
validation_dogs_dir = os.path.join(validation_dir, 'dogs')

Разбираемся с данными и их структурой

Давайте посмотрим сколько же у нас изображений кошек и собак в тестовом и валидационном наборах данных (директориях).

num_cats_tr = len(os.listdir(train_cats_dir))
num_dogs_tr = len(os.listdir(train_dogs_dir))

num_cats_val = len(os.listdir(validation_cats_dir))
num_dogs_val = len(os.listdir(validation_dogs_dir))

total_train = num_cats_tr + num_dogs_tr
total_val = num_cats_val + num_dogs_val

print('Кошек в тестовом наборе данных: ', num_cats_tr)
print('Собак в тестовом наборе данных: ', num_dogs_tr)

print('Кошек в валидационном наборе данных: ', num_cats_val)
print('Собак в валидационном наборе данных: ', num_dogs_val)
print('--')
print('Всего изображений в тренировочном наборе данных: ', total_train)
print('Всего изображений в валидационном наборе данных: ', total_val)

Вывод последнего блока будет следующим:

Кошек в тестовом наборе данных:  1000
Собак в тестовом наборе данных:  1000
Кошек в валидационном наборе данных:  500
Собак в валидационном наборе данных:  500
--
Всего изображений в тренировочном наборе данных:  2000
Всего изображений в валидационном наборе данных:  1000

Установка параметров модели

Для удобства мы вынесем установку переменных, которые нам понадобятся для дальнейшей обработки данных и тренировки модели, в отдельное объявление:

BATCH_SIZE = 100 # количество тренировочных изображений для обработки перед обновлением параметров модели
IMG_SHAPE = 150 # размерность 150x150 к которой будет преведено входное изображение

Подготовка данных

Перед тем как изображения могут быть использованы в качестве входных данных для нашей сети их необходимо преобразовать к тензорам со значениями с плавающей запятой. Список шагов, которые необходимо предпринять для этого:

1. Прочитать изображения с диска
2. Декодировать содержимое изображений и преобразовать в нужный формат с учетом RGB-профиля
3. Преобразовать к тензорам со значениями с плавающей запятой
4. Произвести нормализацию значений тензора из интервала от 0 до 255 к интервалу от 0 до 1, так как нейронные сети лучше работают с маленькими входными значениями.

К счастью все эти операции могут быть выполнены с использованием tf.keras.preprocessing.image.ImageDataGenerator-класса.

Всё это мы можем сделать с использованием нескольких строк кода:

train_image_generator = ImageDataGenerator(rescale=1./255)
validation_image_generator = ImageDataGenerator(rescale=1./255)

После того как мы определили генераторы для набора тестовых и валидационных данных, метод flow_from_directory загрузит изображения с диска, нормализует данные и изменит размер изображений — всего лишь одной строкой кода:

train_data_gen = train_image_generator.flow_from_directory(batch_size=BATCH_SIZE,
                                                          directory=train_dir,
                                                          shuffle=True,
                                                          target_size=(IMG_SHAPE,IMG_SHAPE),
                                                          class_mode='binary')

Вывод:

Found 2000 images belonging to 2 classes.

Генератор по валидационным данным:

val_data_gen = validation_image_generator.flow_from_directory(batch_size=BATCH_SIZE,
                                                              directory=validation_dir,
                                                              shuffle=False,
                                                              target_size=(IMG_SHAPE,IMG_SHAPE),
                                                              class_mode='binary')

Вывод:

Found 1000 images belonging to 2 classes.

Визуализируем изображения из тренировочного набора

Мы можем визуализировать изображения из тренировочного набора данных воспользовавшись matplotlib:

sample_training_images, _ = next(train_data_gen)

Функция next возвращает блок изображений из набора данных. Один блок представляет собой кортеж из (множество изображений, множество меток). В данный момент мы отбросим метки, так как они нам не нужны — нас интересуют сами изображения.

# данная функция отрисует изобраэения в сетке размером 1х5
def plotImages(images_arr):
  fig, axes = plt.subplots(1, 5, figsize=(20, 20))
  axes = axes.flatten()
  for img, ax in zip(images_arr, axes):
    ax.imshow(img)
  plt.tight_layout()
  plt.show()

plotImages(sample_training_images[:5]) # отрисовываем изображения 0-4

Пример вывод (2 изображения вместо всех 5):

Создание модели

Описываем модель

Модель состоит из 4 блоков свёртки после каждого из которых следует блок со слоем подвыборки. Далее у нас идёт полносвязный слой с 512 нейронами и функцией активации relu. Модель выдаст распределение вероятностей по двум классам — собаки и кошки — используя softmax.

model = tf.keras.models.Sequential([
    tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(IMG_SHAPE, IMG_SHAPE, 3)),
    tf.keras.layers.MaxPooling2D(2, 2),

    tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
    tf.keras.layers.MaxPooling2D(2, 2),

    tf.keras.layers.Conv2D(128, (3, 3), activation='relu'),
    tf.keras.layers.MaxPooling2D(2, 2),

    tf.keras.layers.Conv2D(128, (3, 3), activation='relu'),
    tf.keras.layers.MaxPooling2D(2, 2),

    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(512, activation='relu'),
    tf.keras.layers.Dense(2, activation='softmax')
])

Компилирование модели

Как и ранее мы воспользуемся оптимизатором adam. В качестве функции потерь воспользуемся sparse_categorical_crossentropy. Так же мы хотим на каждой обучающей итерации следить за точностью модели, поэтому передаём значение accuracy в параметр metrics:

model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

Представление модели

Давайте взглянем на структуру нашей модели по уровням используя метод summary:

model.summary()

Вывод:

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 148, 148, 32)      896       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 74, 74, 32)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 72, 72, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 36, 36, 64)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 34, 34, 128)       73856     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 17, 17, 128)       0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 15, 15, 128)       147584    
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 7, 7, 128)         0         
_________________________________________________________________
flatten (Flatten)            (None, 6272)              0         
_________________________________________________________________
dense (Dense)                (None, 512)               3211776   
_________________________________________________________________
dense_1 (Dense)              (None, 2)                 1026      
=================================================================
Total params: 3,453,634
Trainable params: 3,453,634
Non-trainable params: 0

Тренировка модели

Настала пора тренировки модели!

Так как обучающие блоки будут поступать из генератора (ImageDataGenerator) мы воспользуемся методом fit_generator вместо ранее используемого метода fit:

EPOCHS = 100
history = model.fit_generator(
    train_data_gen,
    steps_per_epoch=int(np.ceil(total_train / float(BATCH_SIZE))),
    epochs=EPOCHS,
    validation_data=val_data_gen,
    validation_steps=int(np.ceil(total_val / float(BATCH_SIZE)))
)

Визуализация результатов тренировки

Теперь мы визуализируем результаты тренировки нашей модели:

acc = history.history['acc']
val_acc = history.history['val_acc']

loss = history.history['loss']
val_loss = history.history['val_loss']

epochs_range = range(EPOCHS)

plt.figure(figsize=(8,8))
plt.subplot(1, 2, 1)
plt.plot(epochs_range, acc, label='Точность на обучении')
plt.plot(epochs_range, val_acc, label='Точность на валидации')
plt.legend(loc='lower right')
plt.title('Точность на обучающих и валидационных данных')

plt.subplot(1, 2, 2)
plt.plot(epochs_range, loss, label='Потери на обучении')
plt.plot(epochs_range, val_loss, label='Потери на валидации')
plt.legend(loc='upper right')
plt.title('Потери на обучающих и валидационных данных')
plt.savefig('./foo.png')
plt.show()

Вывод:

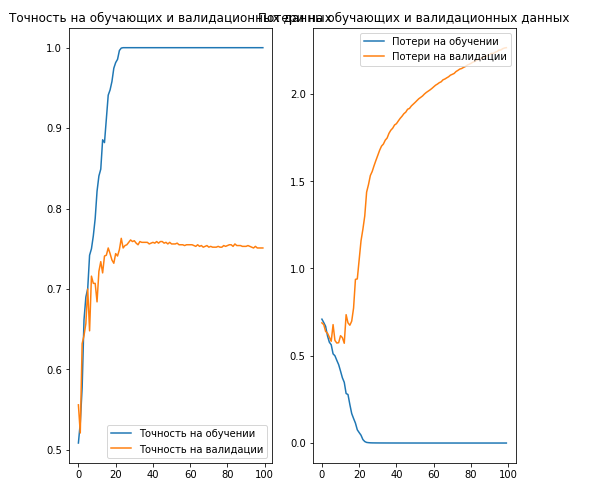
Как можно заметить на графиках, точность на тренировочном и валидационном наборах данных различаются на достаточно большое значение и наша модель достигла всего лишь 70% точности на валидационном наборе данных (зависит от количества обучающих итераций).

Это является очевидным свидетельством переобучения. Как только кривые обучения и валидации начинают расходиться это значит, что модель начинает запоминать тренировочные данные и плохо отрабатывать на валидационном наборе данных.

Продолжение следует… в новой публикации.

… и стандартные call-to-action — подписывайся, ставь плюс и делай share :)

YouTube
Telegram
ВКонтакте

Автор: Андрей Шмиг

Источник