27 октября 2017 года появилась статья доктора Джофри Хинтона с соавторами из Google Brain. Хинтон — более чем известный ученый в области машинного обучения. Он в свое время разработал математику обратного распространения ошибок, был научным руководителем Яна Лекуна — автора архитектуры сверточных сетей.
Хоть презентация была достаточно скромная, корректно говорить о революционном изменении подхода к искусственным нейронным сетям (ИНС). Назвали новый подход «капсульные сети». Пока в российском сегменте интернета мало информации о них, поэтому восполню этот пробел.
Итак, как оказалось, Хинтон последние годы искал идеи, которые позволят сделать что-то круче, чем сверточные сети в компьютерном зрении. Что ему не нравилось в CNN (convolutional neural networks, сверточные нейронные сети)? В основном, слой max-pooling и инвариантность детектирования лишь к положению на изображении. Он используется для уменьшения размерности выходов сверточных слоев, игнорирования небольших отличий в пространственной структуре изображений (или других типов данных).
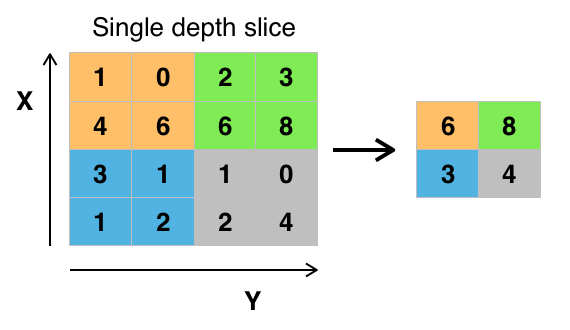
Из изображения понятно как этот слой работает: выбирает максимум в окне выхода сверточного слоя. При этом теряется часть информации. На самом деле это не так очевидно доказать, и даже могут быть классы объектов, для которых потери информации не случается. Кроме того, в ряде архитектур сверточных сетей слоя max-pooling просто нет. Но, тем не менее, — max-pooling действительно достаточно уязвимый для критики слой.
Еще больше критики сверточных сетей есть в конце одной из прошлых моих статей. О похожих проблемах говорит и Хинтон.
Кроме того, большой «слон», которого мы, инженеры, стараемся не замечать в своей комнате — миниколонки в коре , которые явно должны иметь понятную, ограниченную и не слишком примитивную функцию.
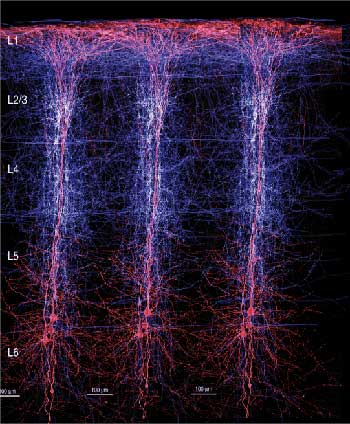
Так Хинтон и говорит: нейронные капсулы — миниколонки, они могут соответствовать узнаваемым объектам, их характеристикам. Суммарная активность нейронов характеризует вероятность узнавания. Выходной информации внутри капсулы должно быть достаточно, чтобы восстановить входную почти без потерь.
Архитектура
Для тех, кто немного занимался сверточными сетями, эта картинка объясняет уже почти все:
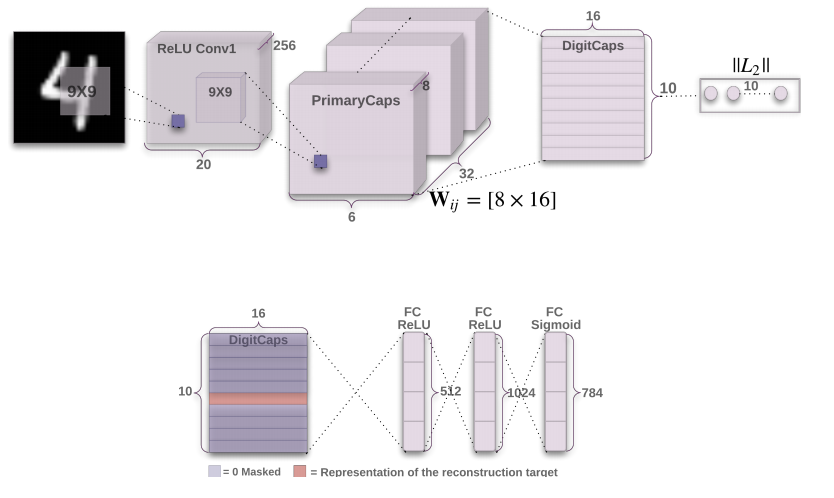
Итак, сначала идет стандартное выделение фич, инвариантных к трансляции на изображении, с помощью сверточного слоя. Даже если вы не знаете, что такое сверточный слой, то все равно можете читать дальше — здесь это не критично.
Затем выделяются еще 32 сверточных слоя, каждый из которых смотрит на первый сверточный слой. Вот это уже необычно, а картинка совсем не объясняет зачем. Для динамического роутинга (конечно, маршрутизации, но пусть будет роутинг, иначе выглядит будто речь о сетевых технологиях). Это одна из двух «фишек», которая отличает данную архитектуру от остальных, поэтому заслуживает отдельной главы.
Потом идет слой «digitCaps» — собственно те капсулы, о которых говорит Хинтон. Хоть он и называет предыдущий слой «primaryCaps», т.е. первичные капсулы, особо новой функции сами по себе они не несут. Важно лишь то, как они затем соединяются с «digitCaps».
Так вот, каждая капсула (или миниколонка) имеют строгий смысл: амплитуда вектора в каждой из них соответствует вероятности наличия в изображении одной из цифр.
Внизу изображения притаилась достаточно важная часть архитектуры: декодер, на вход которого подается слой DigitCaps, при этом все капсулы обнуляются кроме одной, которая «выиграла» по амплитуде. Декодеры — по сути инвертированная ИНС (искусственная нейронная сеть), на входе которой небольшой вектор, а на выходе — исходное изображение. Этот декодер обеспечивает вторую самую важную «фишку» этой архитектуры: содержимое одной капсулы должно полностью описывать подмножество конкретной цифры, подаваемое на вход. Иначе декодер никак не сможет восстановить исходное изображение. Есть и другое полезное свойство у декодера — это способ регуляризации. Близкие коды в капсулах будут у близких по Евклиду изображений.
Например, в статье приводится результат «шевеления» компонент в одной из капсул (в данном случае ответственной за цифру 6):

Компоненты вектора-капсулы ответственны за форму представления цифры по Хинтону.
Динамический роутинг
Hinton, Frosst и Sara Sabour пишут: «есть много способов реализовать идею капсульных сетей. И динамический роутинг в предложенном виде — лишь один из примеров». Поэтому может оказаться, что вскоре появятся более элегантные решения. Но пока что работает всё следующим образом:
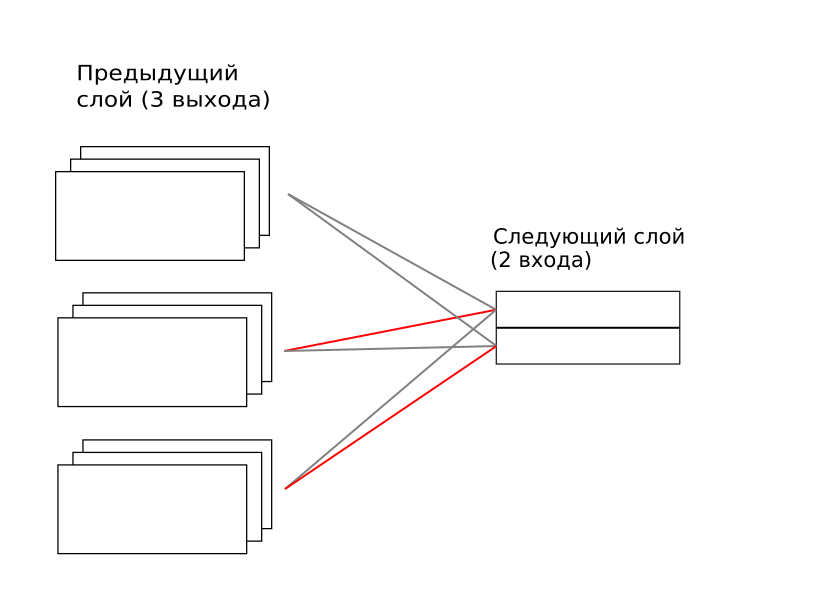
Каждая капсула из предыдущего слоя соединена с каждой следующей. Здесь «соединена» значит, что есть весовая матрица между каждой капсулой из предыдущего слоя и каждой следующего. Эти веса тренируются, как в обычной искусственной нейронной сети методом обратного распространения ошибок. Но поверх этих весов коэффициентами накладывается ещё множитель для каждой пары, при этом множитель в итоге должен стремиться к единице или нулю. В пределе каждая капсула из верхнего уровня «слушает» только одну капсулу из нижнего в один момент. На изображении сверху первая капсула из верхнего уровня обращает внимание только на вторую капсулу нижнего, а вторая в верхнем — только на третью из нижнего. Обратите внимание, что эта матрица временная и должна рассчитываться для каждого примера заново. Далее так и буду называть ее «временная матрица». А вот полносвязные весовые матрицы между всеми капсулами обучаются и их веса существуют всегда, несмотря на то, что не каждый раз реализуются.
Как рассчитывается эта временная матрица? Довольно хитрым итерационным процессом: при предъявлении нового примера капсульной сети оценивается, какой вклад в вектор капсулы верхнего уровня дает каждое соединение с нижним уровнем. То соединение, которое дает больший вклад, увеличивает свой вес во временной матрице, а затем всё нормализуется, чтобы коэффициенты не уходили в бесконечность. И так повторяется 3 раза.
Здесь не очевидно, но, на самом деле, это реализация принципа «победитель забирает всё». Ну, из-за итерационного принципа здесь «победитель забирает почти всё». И так происходит распределение ролей на нижнем уровне: каждый элемент начинает лучше описывать какую-то свою ситуацию для каждой из капсул верхнего уровня.
Таким образом, при распознавании (как и при обучении) для каждой капсулы, ответственной за конкретную цифру, решается задача: модель какой из капсул нижнего уровня лучше описывает наблюдаемое изображение. А потом уже оценивается амплитуда каждого из векторов в капсулах верхнего уровня для принятия решения, какая цифра наиболее вероятна.
Если захотите разобраться в математике детально, то она описана в оригинальной статье. И ещё более подробно здесь.
Результаты экспериментов
Экспериментировали на хорошо известной базе изображений MNIST, в которой представлено 10 цифр прописью в различных вариациях.
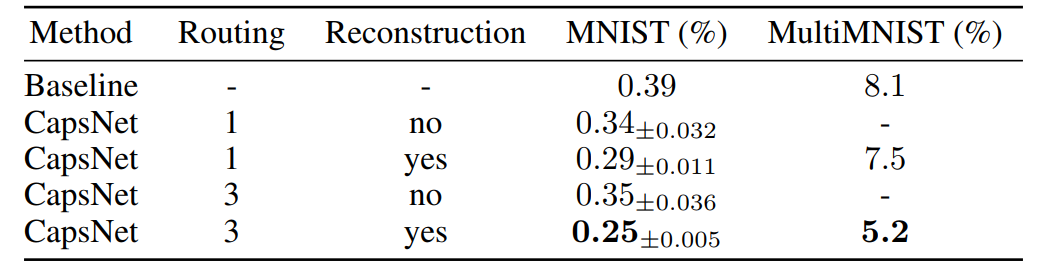
О чем эти строки? Добавление декодера и динамический роутинг с тремя итерациями помогает. Во втором столбце результат на MNIST, когда 2 цифры наложены друг на другу. Это интересная способность капсульных сетей выбрать не одну капсулу победителя, а сразу две. Единственное, не сработает в случае, если две одинаковые цифры нарисованы поверх друг друга немного разным образом.
ИМХО на MNIST можно получить любую точность. Размер тестовой выборки 10000, значит, при 99,7% точности есть лишь 30 ошибок. А изменяя те или иные параметры алгоритма, всегда можно понизить эту ошибку за счет лишь случайностей. Поэтому можно лишь говорить о вкладе того или иного механизма в результат (и то, на самом деле, он будет спорным и статистически недостоверным). Например, весь механизм динамического роутинга даёт улучшение лишь на 0.04%, т.е. на 4 изображения. Значит, было 29 ошибок, стало 25. Вероятность того, что динамический роутинг не помог, все ещё весьма серьёзная.
Конечно, думаю, всё это работает и помогает. Просто не стоит обращать внимание на результат на MNIST. Важна сама концепция, а MNIST позволил отладить и проверить её реализацию. И это важный шаг — теперь мы все можем потрогать реализацию, например в tensorflow, и разобраться в том, как она работает, лично.
Что это всё значит? Сильный ИИ, который нас всех поработит?
Из-за динамичного развития концепции сверточных сетей (а еще рекуррентных, но Хинтон не объясняет, как его идеи могут поглотить и их, хотя могут) еще пару лет назад всем в отрасли начало казаться, что вот больше ничего и не надо. Всё тренируется — дайте данные! И лишь вопрос времени, когда все задачи решатся. Но это не так. И я считаю, что это очень важно, что человек, считающийся отцом Deep learning, говорит о суровой ущербности существующих подходов, ищет новые направления.
А значит, что с 27 октября 2017 года больше групп исследователей займутся поиском следующего шага в искусственном интеллекте, больше людей будут формулировать, чем же отличается «слабый» ИИ от «сильного», начнётся конкуренция среди ранее маргинальных, а в последствии трендовых, теорий, которые должны прийти на смену существующим моделям. И это всё очень хорошо! Сейчас открывается новый Дикий Запад в области ИИ.
Анонс, пользуясь случаем
Не так давно, в этой статье, вооружившись идеями Алексея Редозубова, которые практически ортогональны существующему устоявшемуся консенсусу, я на примере автомобильных номеров пытался показать альтернативный подход.
Последний год наши изыскания тоже не стояли на месте. Мы, например, написали демонстрацию на MNIST на Keras, которой теперь даже не стыдно и поделиться с сообществом. А капсульные сети лишь убедили, что формулировка функции миниколонок крайне важна на текущем этапе, и у нас она несколько отличается от той, что дает Хинтон (конечно, в лучшую сторону).
Поэтому, в ближайшие дни опубликую аналогичную статью по следам тренировки MNIST и статьи на arxiv в рамках концепции «совсем не нейронных сетей» (название что-то никак не придумаем).
Автор: Моржаков Василий