Привет! За последние годы новые подходы в обучении нейронных сетей позволили существенно расширить сферы практического применения машинного обучения. А появление большого количества хороших высокоуровневых библиотек дало возможность проверить свои навыки специалистам разного уровня подготовки.
Имея некоторый опыт в машинном обучении, я до текущего момента не имел дело конкретно с нейронными сетями. На волне их стремительной популярности было принято решение заполнить данный пробел и заодно попробовать написать об этом статью.
Я поставил себе две цели. Первая, придумать задачу, достаточно сложную чтобы при её решении столкнуться с проблемами, возникающими в реальной жизни. И вторая, решить эту задачу с использование одной из современных библиотек, разобравшись с особенностями работы с ними.
В качестве библиотеки был выбран TensorFlow. А за задачей и её решением прошу под кат…
Выбор задачи
Пытаясь придумать задачу, я руководствовался следующими соображениями:
- Это должно быть что-то более сложное и интересное нежели чем стандартная MNIST классификация, так как я искал возможности столкнуться с конкретными особенностями обучения нейронных сетей;
- В качестве архитектуры планировалась нейронная сеть прямого распространения (feedforward), так как знакомство всегда лучше начинать с простых вещей;
- Обучение должно работать достаточно быстро на обычной игровой видеокарте, так как все делалось в свободное от основной работы время.
Бродя по интернету и изучая материал, я в числе прочего наткнулся на следующие статьи:
- [1] A neural algorithm of artistic style [arXiv] в которой представлен подход обработки изображений в стиле известных художников. Развитие данного направления позже привело к появлению популярного сервиса Prisma;
- [2] Learning to Generate Chairs, Tables and Cars with Convolutional Networks [arXiv] в которой предложен способ генерации изображений, в частности стульев, по заданным параметрам таким как цвет или угол обзора.
Именно эти статьи, а также требование к скорости обучения подсказали мне идею задачи.
Задача
Для большинства шрифтов, доступных в сети, существуют только латинские версии. А что если используя лишь изображения латинских букв восстановить его кириллическую версию с сохранением оригинального стиля?
Сразу оговорюсь, я не ставил целью сделать конечный продукт готовый для применения в издательстве. Моей целью было обучится работать с нейронными сетями. Поэтому я ограничился работой с растровыми изображениями размера 64×64 пикселя.
Выбор библиотеки
Среди существующего зоопарка пакетов и библиотек мой выбор пал на TensorFlow по следующим причинам:
- Библиотека достаточно низкоуровневая в сравнение например с Keras, что с одной стороны сулило какое-то количество шаблонного кода, а с другой — возможность разобраться в деталях и попробовать нестандартные архитектуры;
- TensorFlow поддерживает обучение на нескольких машинах/видеокартах. Поэтому полученные навыки работы с библиотекой могут пригодится на реальных практических задачах;
- Инструмент TensorBoard в составе TensorFlow позволяет легко следить за процессом обучения в интерактивном режиме. Среди прочего это позволило обнаруживать ошибки в коде на ранних этапах обучения и не тратить время на заведомо плохие архитектуры и наборы параметров.
Архитектура сети
Все шрифты обладают индивидуальными особенностями. Рядовой пользователь скорое всего вспомнит про курсив или толщину, а специалист в типографщике не забудет про антиквы, гротески и другие красивые слова.
Такие индивидуальные особенности тяжело поддаются формализации. При обучении нейронных сетей типовым подходом решения данной проблемы является использование embedding слоя. Если коротко, то делается попытка сопоставить моделируемому объекту одномерный числовой вектор. Семантика отдельных компонент вектора при этом останется неизвестной, однако, как ни странно, целый вектор позволяет моделировать объект в контексте задачи. Наиболее известным примером такого подхода является модель Word2Vec.
Я решил сопоставить каждому шрифту вектор $inline$f$inline$ и каждой букве вектор $inline$l$inline$. Изображение $inline$I$inline$ конкретной буквы для данного шрифта получается при помощи нейронной сети $inline$G$inline$, на вход которой подаются два вектора, соответствующих шрифту и букве.
$$display$$I=G[f, l]$$display$$
Важно заметить, что один и тот же вектор $inline$l$inline$ используется при построении изображений отдельной буквы в стилях разных шрифтов (аналогично для отдельного шрифта).
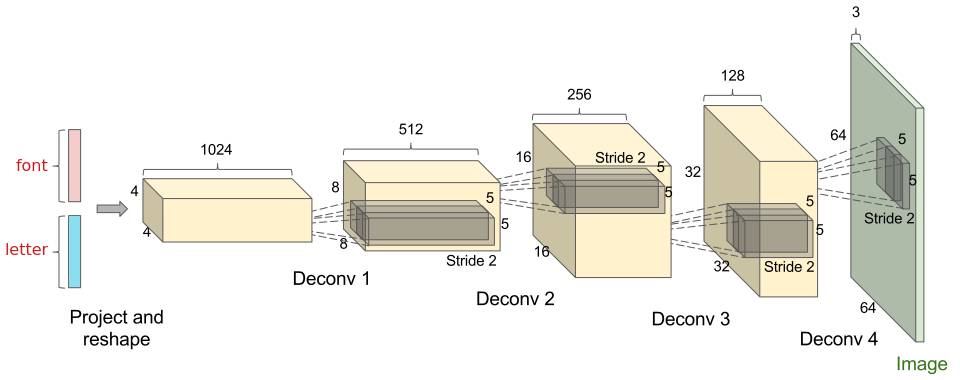
В качестве сети $inline$G$inline$ выступает развёртывающая (deconvolution) нейронная сеть. Изображение выше взято из блога openai.com для демонстрации. Боле подробно об используемой операции развёртывания и количестве слоёв в сети речь пойдёт далее.
Обучение модели
Обучающая выборка $inline$T$inline$ состоит из изображений русских и латинских букв. Для каждого изображения известна буква и используемый шрифт.
На этапе обучения мы ищем веса сети $inline$G$inline$ и embedding вектора для всех букв и шрифтов из обучающей выборки используя одну из вариаций метода стохастического градиента.
$$display$$underset{G,l,f}{argmin}sum_{I in T}L(I,G[f_I,l_I])$$display$$
В качестве функции потерь $inline$L$inline$ используется суммарная перекрёстная энтропия (cross entropy) между предсказанными и настоящими пикселями (значение пикселя масштабировано от нуля до единицы).
Восстановление изображений
Обученная нейронная сеть $inline$G$inline$ и embedding вектора кириллических и латинских символов используются в поставленной выше задаче восстановления кириллических шрифтов.
Допустим нам на вход поступил латинский шрифт $inline$u$inline$, отсутствующий в обучающей выборке. Мы можем попытаться восстановить его embedding вектор $inline$f_u$inline$, используя только изображения латинских букв $inline$R$inline$. Для этого решим следующую оптимизационную задачу:
$$display$$f_u=underset{f}{argmin}sum_{I in R}L(I,G[f,l_I])$$display$$
Эта задача может уже решаться методом обычного градиентного спуска (или любым другим), так как мощность множества $inline$R$inline$ около двух-трёх десятков букв.
Далее, используя полученные на этапе обучения embedding вектора кириллических символов и embedding вектор $inline$f_u$inline$, мы с лёгкостью можем восстановить соответствующие изображения при помощи сети $inline$G$inline$.
Подготовка обучающей выборки
Как это часто бывает, значительная доля времени ушла на подготовку обучающей выборки. Началось все с того, что я зашёл на известные в узких кругах сайты и скачал доступные там коллекции шрифтов. Разархивированный размер всех файлов составил ~ 14 GB.
Сначала оказалось, что для разных шрифтов буквы одного размера могут занимать разное количество пикселей. Для борьбы с этим была написана программа, подбирающая размер шрифта, чтобы уместить все его символы в изображение 64 на 64 пикселя.

Далее все шрифты условно были разделены на три вида — классические, экзотические и орнаментальные. На последних может быть изображено все что угодно кроме кириллических и латинских символов, например, смайлики или картинки. На экзотических шрифтах все буквы на месте, однако изображены особым образом. Например на экзотических шрифтах могут быть инвертированы цвета, добавлены рамочки, использоваться пропись и так далее.
На глаз орнаментальные шрифты составляли большую долю в коллекции, а ничем кроме шума их считать нельзя. Встала задача их фильтрации. К сожалению, используя метаданные это не получилось сделать. Вместо этого я стал считать количество одноцветных областей в черно-белых изображениях отдельных букв и сравнивать его с эталонным значением. Например, букве А соответствует эталонное число три, а букве Т два. Если в шрифте достаточно много букв с отличиями от эталонных значений, он считается шумом.
В итоге была так же отсеяна значительная часть экзотических шрифтов. Я не сильно расстроился, так как не питал особых иллюзий об обобщающей способности разрабатываемой сети. Итоговой размер коллекции получился ~ 6000 шрифтов.
О сверточных нейронных сетях
Если вы дочитали до текущего момента, думаю вы имеете представление о сверточных (convolution) нейронных сетях. Если нет, в сети достаточно материала на данную тему. Здесь я хочу лишь отметить два момента о сверточных сетях:
- Их способность давать на выходе последних слоёв множество характеристик исходного изображения, комбинация которых можно использовать при его анализе ([3] Deep Convolutional Neural Networks as Generic Feature Extractors [PDF]);
- Эти глобальные характеристики, получаются через последовательное вычисление локальных характеристик во внутренних слоях нейронной сети.
В контексте статьи, первое утверждение наводит на аналогию межу получаемыми характеристиками и описанным выше embedding слоем. А второе даёт интуитивное обоснование попробовать постепенно восстанавливать локальные характеристики исходного изображения из глобальных.
Деконволюции
Используемая в сверточных сетях функция convolution + ReLu + maxpooling не является обратимой. В литературе предложено несколько способов [2][4] её «восстановления». Я решил воспользоваться самым простым — convolution transpose + ReLu, что по сути является линейной функцией + простейшая нелинейная функция активации. Главным для меня было сохранить свойство локальности.
В TensorFlow есть функция conv2d_transpose, которая осуществляет данное линейное преобразование. Основной проблемой, с которой я здесь столкнулся, было представить, как именно выполняется вычисление, чтобы рационально подобрать параметры. Здесь мне на помощь пришла иллюстрация для одномерного случая из статьи [5] MatConvNet — Convolutional Neural Networks for MATLAB (стр. 30) [arXiv]:
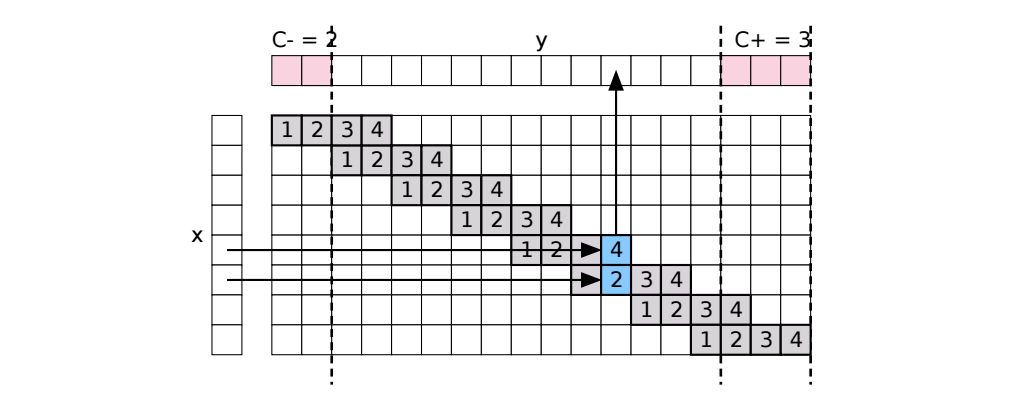
В итоге я остановился на параметрах stride = [2, 2] и kernel = [4, 4]. Это позволило в каждом deconvolution слое увеличивать длину и ширину изображения в два раза и использовать группы из 4 соседних пикселей для вычисления нейронов следующего слоя.
Процесс обучения
При обучении сети я столкнулся с двумя моментами, которыми думаю будет полезным поделиться.
Во первых, очень важным оказалось сбалансировать количество кириллических и латинских изображение в обучающей выборке. Сначала латинских символов в моей обучающей выборке получилось сильно больше, как результат сеть лучше рисовала их, в ущерб качеству восстановления кириллических символов.
Во вторых, при обучение помогло постепенное уменьшение learning rate градиентного спуска. Я делал это вручную, следя за ошибкой в TensorBoard, однако в TensorFlow существуют возможности для автоматизации этого процесса, например используя функцию tf.train.exponential_decay.
Другими полезными трюками как регуляризация, dropout, batch normalization пользоваться не пришлось, так как и без них получилось добиться результатов приемлемых для моих целей.
Итоговые параметры сети
Размерность embedding слоя 64 и для символов и для шрифтов.
4 deconvolution слоя внутренних слоёв 8×8×128→16×16×64→32×32×32→64×64×16, stride = [2, 2], kernel = [4, 4], ReLu активация
1 convolution слой 64×64×16→64×64×1, stride = [1, 1], kernel = [4, 4], SoftMax активация
Результаты
Для демонстрации результатов аккурат недавно нашёлся информационный повод, когда сразу два российских проекта МойОфис и Astra Linux выпустили свободные коллекции шрифтов. Данные шрифты не были использованы в обучающей выборке. Слева оригинальный шрифт, справа выход нейронной сети. Для компактности приведены только кириллические буквы, у которых нет латинских аналогов.
XOCourserBold

PTAstraSansItalic

XOThamesBoldItalic

PTAstraSerifRegular

Остальные
Остальные результаты выкладываю отдельным архивом.
Итог
Получив данные результаты, считаю, что поставленных целей я добился. Хотя стоит отметить, что они далеки от идеальных (особенно заметно для некоторых Italic шрифтов) и ещё есть много вещей, которые можно добавить, усовершенствовать и проверить.
Какой же получилась статья, судить Вам.
Ссылки по теме
[1] Gatys, Ecker, Bethge, A neural algorithm of artistic style [arXiv]
[2] Dosovitskiy, Springenberg, Tatarchenko, Brox, Learning to Generate Chairs, Tables and Cars with Convolutional Networks [arXiv]
[3] Hertel, Barth, Käster, Martinetz, Deep Convolutional Neural Networks as Generic Feature Extractors [PDF]
[4] Zeiler, Krishnan, Taylor, Fergus, Deconvolutional Networks [PDF]
[5] Vedaldi, Lenc, MatConvNet — Convolutional Neural Networks for MATLAB [arXiv]
Автор: artem_panasyuk

