Наверняка всякий, кто встречался с «перлиновым шумом» (perlin noise), пробовал генерить текстуру облаков.
Потомучто оно само напрашивается.
О шуме Перлина на хабре уже была статья, но в ней очень мало картинок.
Вкратце, суть перлинового шума такова: равномерно распределённые случайные точки соединяются плавным градиентом.
Выглядит это не особо привлекательно:

Однако, если взять только верхнюю половину волн, умельчить в 2 раза, в 4, и в 8, и сложить всё это, получатся весьма узнаваемые облака:
 +
+  +
+  +
+  =
= 
Почти тоже самое, но 8 раз:

По загогулине в центре видно, что такая конструкция фрактальна, и неизбежно обладает точкой схода (fixed point). Соседние загогулины тоже на неё намекают. На практике это особо не мешает, или её можно засунуть куда-нибудь подальше.
Вот как происходит формирование облаков в текстурном пространстве:

Возникает резонный вопрос — а зачем уровни масштабируются именно в два раза?
Вот пример 8ми-уровневого облака с разными коофициантами масштабирования:
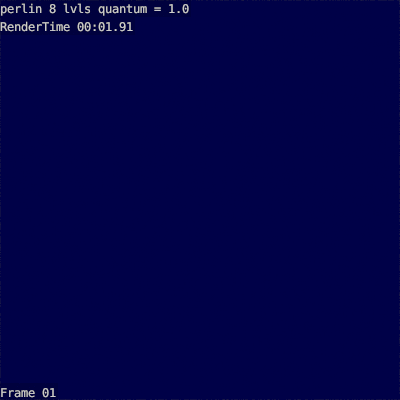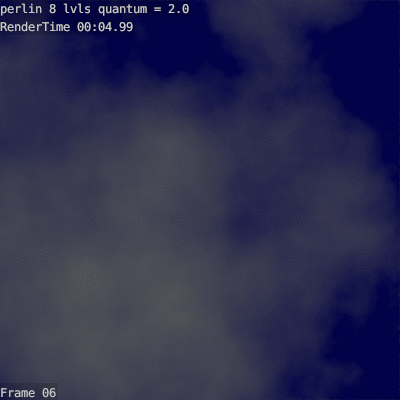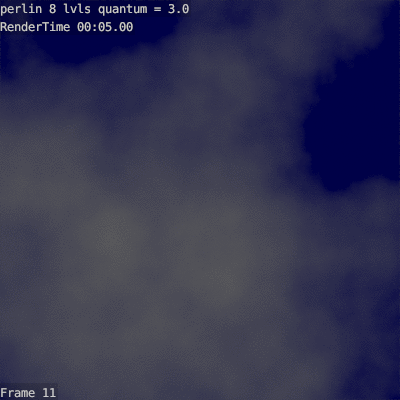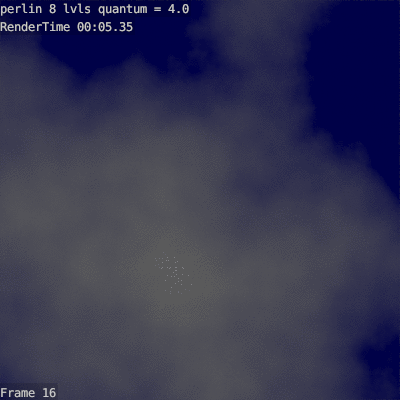
Видно, что до 1.6 облако недостаточно кудряво, а после 2.6 слишком пупырчато.
Можно попробовать подставить волшебные числа:

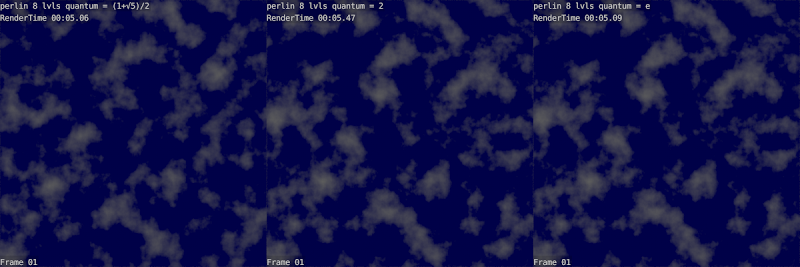
Золотое сечение чуть более размазано, число e чуть более кучнее.
Никакого чуда не произошло. Хотя иногда с числами оно случается.
Два.
Итак, формула клёвого облака такова:
float acc = 0.0;
float amp = 1.0;
int i;
for(i=0; i<layers; i++){
float v = noise("perlin", scale*pnt);
acc += v * amp;
amp *= .5;
scale *= 2.0;
}
// max(acc) = (2^n - 1) / 2^n
acc *= (float)(1<<(layers)) / (float)((1<<(layers)-1));
return acc * 0.5 + 0.5;
}
Здесь pnt — точка в пространстве текстуры для которой вычисляется фактор облака. Например, UV.
Функция noise(method, coords) генерит значении perlin noise для заданной точки, в диапазоне от -1 до +1.
Есть, наверняка, в любой графической библиотеке, а также в упомянутой выше хабрастатье.
Вооружившись этой формулой, можно генерить эту текстуру в 3d, и натянуть её на сферу (не заморачиваясь со сферическими проекциями, а просто подставив координаты точки сферы в пространстве):

Ещё можно сгенерить четырёхмерную текстуру, и, сдвигая по времени, получить живые облака:

Для пущей убедительности, текстурную 3d-координату можно ещё повернуть вдоль экватора на 30 градусов, пропорционально квадрату косинуса широты:

Почему 30 градусов и квадрат косинуса — не знаю, но именно так выглядят реальные облака на планете.
На самом деле, реальные облака на планете Земля, по версии NASA (http://visibleearth.nasa.gov/) выглядят так:

А полученная текстура имеет с ними мало общего.
Во-первых, облака надо раскучерявить.
Для раскучерявливания нужно для каждой точки сместить текстурную координату в каком-нибудь направлении, причом так, чтобы у близких точек смещение различалось незначительно. Очевиднее всего для вычисления смещения использовать снова перлинов шум.
if(Distortion != 0.0) {
point sp = scale[0] * pnt.p;
float st = scale[1] * pnt.t;
pnt.p[0] += Distortion * noise("perlin", sp + vector(1,0,0), st);
pnt.p[1] += Distortion * noise("perlin", sp + vector(0,1,0), st);
pnt.p[2] += Distortion * noise("perlin", sp + vector(0,0,1), st);
pnt.t += Distortion * noise("perlin", sp, st + 1);
}
Тут float scale[2] — масштабы в пространстве и времени, pnt — struct { point p; float t; } координаты 4d-точки.
Если попытаться сэкономить на вызовах функции noise — будут получаться всякие непотребства, типа такого:

А нужно, чтобы получилась непрерывно искажённая в пространстве и времени текстура:

Во-вторых, на планете облака распространены весьма рвано, а вблизи выглядят как чистокровный перлонов шум (с масштабами от 8 до 16 от размеров планеты).
Лучшее, что я придумал за неделю — это умножать облака.
Крупная облачность, обозначающая мега-воздушные потоки, умноженная на мелкую, барашковую — даёт в результате барашковую облачность, распространённую по мега-потокам.
 ∗
∗  =
= 
Это уже гораздо больше похоже на правду.

Реальные облака имеют разную степень зернистости, но заморачиваться с этим уже лень.
Была идея сделать ещё одно очень крупное облако и его значение использовать как параметр масштаба для мелких.
Этот фокус не прошёл — на границах масштаба барашковые облака неприлично скукоживаются.
Кроме того, при вращении планеты облака у экватора притормаживают (это и даёт закрученность в 30 градусов), но как это сделать, чтобы текстура не перекручивалась в хлам, а плавненько испарялась — я не придумал.
Вероятно, надо использовать 5d текстуру, и смещать закрученность в 5ом измерении, но bledner и open shading language на которых это сооужалось, 5d не поддерживают. Такая досада…
Впрочем, на фоне настоящей планеты такие облака выглядят вполне достойно:
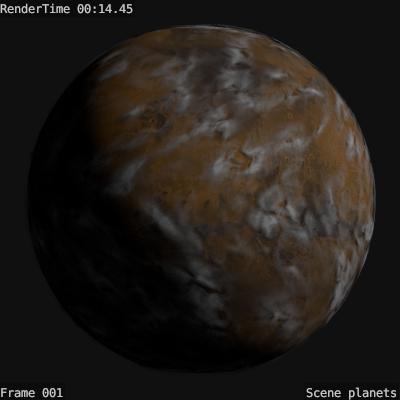
Хотя и рендерятся в 1.5 раза дольше.
Анимированное сравнение nasa vs perlin залито на ютюбе.
Все картинки, включая хайрез «непотребства» лежат в пикасоальбоме.
Ну и blender-file со всеми конструкциями и скриптами на OSL.
Автор: qmax



