Модельно-ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

2014-05-26 в 12:25, admin, рубрики: Без рубрики

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

Привет!

Сегодня я хочу показать простой пример идентификации системы, основываясь на наблюдениях и экспериментальных данных. Это первая и крайне важная ступень в разработке системы управления устройством, которое описать аналитически либо невозможно, либо слишком сложно, ~~либо неохота~~. Для начала рассмотрим метод «черного ящика ~~с котом~~», «серый» и «белый» методы оставим на следующий раз.
Интересующихся прошу под кат.

Оборудование и программное обеспечение в наличии

~~Watchdog~~ Watchduck:

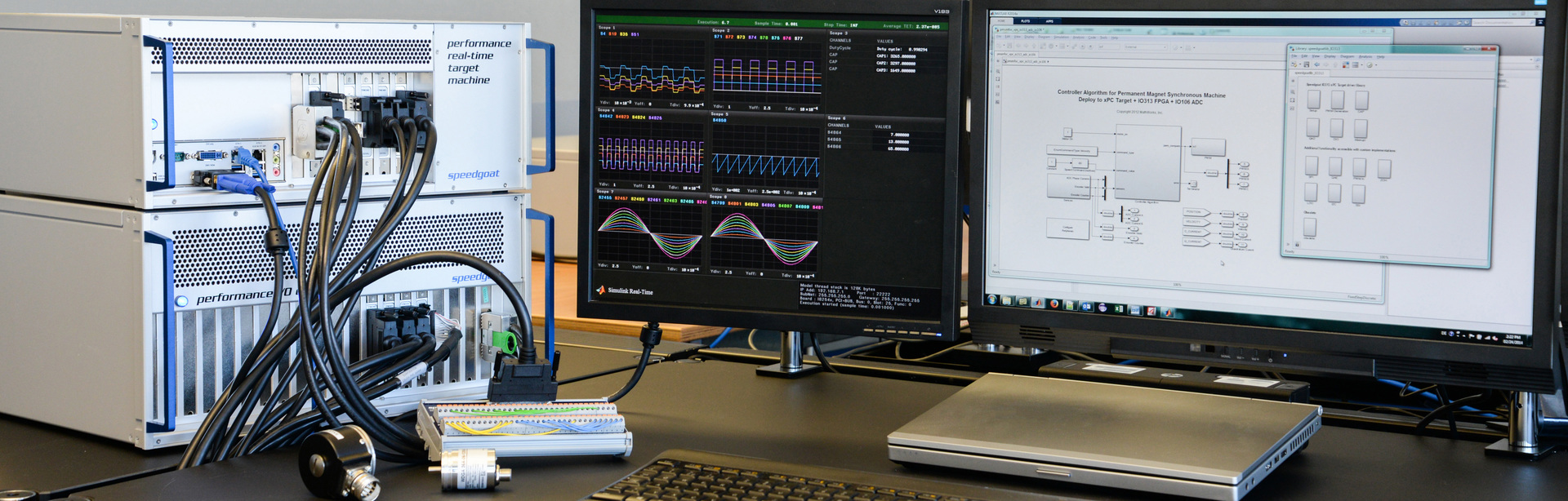
Выполняет ту же функцию, что и Watchdog timer, но применительно к инженеру — помогает выйти из зависания.
Машина реального времени Speedgoat. Немного проще, нежели на заглавной иллюстрации, примерно такая:

В данном ПК (а это по сути и есть IBM совместимый ПК) присутствуют платы ввода-вывода с аналоговыми, дискретными, и прочими входами и выходами, которые я использую как для сбора данных, так и для управления ходом эксперимента. Но самое главное — я могу одним нажатием запускать на ней модели Simulink в режиме жесткого реального времени. О таких машинках (да простят мне уменьшительно-ласкательное дальнейшее к Ней обращение:-) я много еще могу рассказать. Если интересно — можно выделить для этого отдельный топик.
MATLAB/Simulink

Инструментам я не изменяю. Как и в предыдущих моих постах, я буду использовать Simulink для создания моделей, генерировать из них код и запускать его на интересных железках.
Двигатель постоянного тока с энкодером и зубчатой передачей от Pololu. Вот такой:
Arduino + Motor Shield от seeedstudio

Для работы с Arduino из-под Simulink я использую библиотеку Embedded Coder Target for Arduino.
Эта библиотека позволяет использовать модели Simulink для генерации кода полностью готового к компиляции под данную платформу. Можно использовать также встроенную поддержку Arduino в MATLAB/Simulink, но мне данный таргет более по душе.
Макетная плата, проводники, питание и прочая мелочевка

На самом деле, любой из представленных компонентов может быть заменён на соответствующий функциональный аналог (кроме утки, конечно!). Но, так как делалось все «на коленке» — то и право выбора остается за владельцем этого важного сустава.

В собранном виде, если это можно назвать собранностью, все выглядит так:
Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

Постановка задачи

Есть система — необходимо получить её модель для дальнейшей работы. Проще некуда.
Поведение системы и её модели должно максимально совпадать в пределах допустимых входных воздействий. Метод «черного ящика» подразумевает, что мы не будем, или почти не будем, принимать во внимание физику процессов внутри системы, а будем рассматривать её с общей точки зрения теории управления.

В детали я вдаваться в этот раз не буду, поначалу все и так видно, на глаз.
Но следует учесть, что за кулисами остаются архиважные и преинтереснейшие темы — планирование эксперимента (DOE) и дисперсионный анализ (ANOVA), которые заслуживают отдельного рассмотрения.

Целевая система в некотором приближении и с упрощением состоит из следующего набора подсистем:

Дискретная подсистема — Arduino
Непрерывная механическая подсистема — двигатель
Непрерывная электрическая подсистема — Motor Shield

Вход системы — заданное значение ШИМ 0-100%.
Еесть возможность изменять скважность ШИМ сигнала, подавая на выход «аналогового» порта Arduino значения uint8 от 0 до 255. Необходимо узнать, как будет реагировать силовая электроника и двигатель на это воздействие.
Тестовый вектор будет зашит в контроллер, состоит он из 501 элемента и выдается с дискретизацией 0.04с. Итого ~20 секунд тестового воздействия.
Выглядит тестовый вектор так:
Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

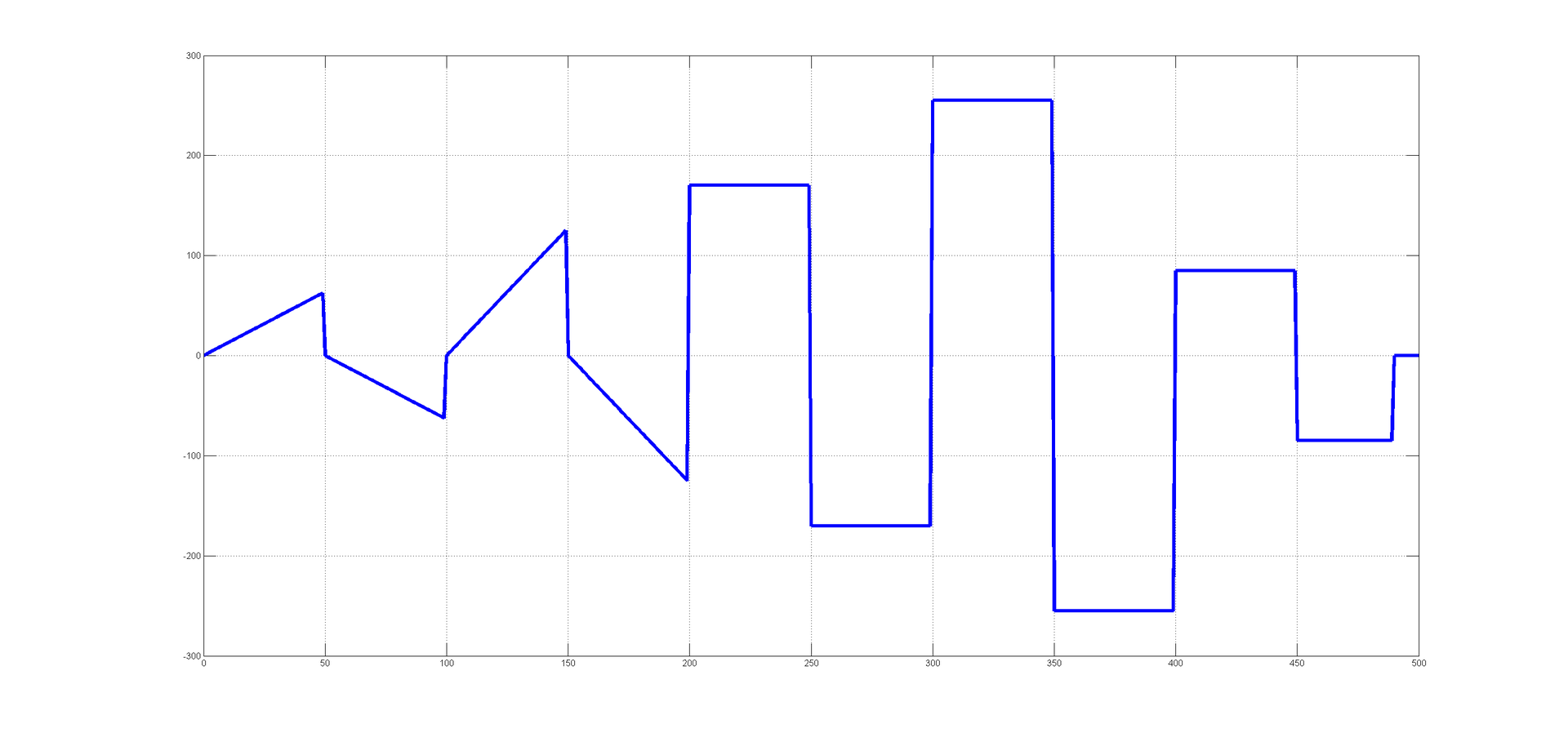
На выходе системы я ожидаю увидеть хоть что-то подобное :-)
Для успешной идентификации тестовый вектор должен покрывать максимальное количество режимов работы системы, в которых она будет, или может работать. Метод «черного ящика» не позволяет в полной мере исследовать аварийные режимы ввиду ограниченности количества экспериментальных образцов. Я буду исследовать систему в рабочих режимах плавного пуска и старт-стоп.

Выход системы — скорость вращения вала, угол поворота вала. С квадратурного энкодера, при вращении вала двигателя, я получаю два меандра со смещением по фазе на pi/2. Их обрабатывает аппаратный декодер, который присутствует на одной из конфигурируемых плат ввода-вывода. При загрузке модели Simulink на машину реального времени происходит «прошивка» ПЛИС (FPGA) для обеспечения требуемых входов/выходов. Тики, с декодера умножаем на коэффициент и превращаем в угол, а скорость изменения их количества в скорость. Энкодер двигателя делает 64 триггирования за один оборот, что позволяет с хорошей точностью отслеживать описанные выше параметры. Основной алгоритм на машине реального времени установлен мною на работу с частотой 10 kHz — на выходе я получаю экспериментальные данные с периодом дискретизации 0,0001с. Аппаратная же часть ПЛИС работает на частоте 33 MHz, что позволяет, помимо основного алгоритма декодирования, успевать применить еще и антидребезговые алгоритмы без ущерба точности измерениям на довольно высоких оборотах. Простыми словами декодирование квадратурного сигнала на FPGA описано в прекрасной статье fpga4fun --> QuadratureDecoder.

Дискретизация величин, временные задержки, моменты инерции механических деталей, трение спокойствия, трение скольжения, трение качения, механический люфт, разбалансировка, резонансные явления, коммутация индуктивных цепей, скользящий контакт, искрение — не полный перечень факторов, с которыми нам пришлось бы столкнуться при попытке описать данную систему аналитически. А ведь это — всего лишь ардуинка с моторчиком!
Соглашусь, некоторыми нюансами вполне можно пренебречь, но на практике, решение пренебречь каким-либо фактором — не самое простое решение.

Так выглядит ШИМ из Arduino (желтый) и напряжение на чисто резистивной нагрузке, которая подключена к шилду:

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

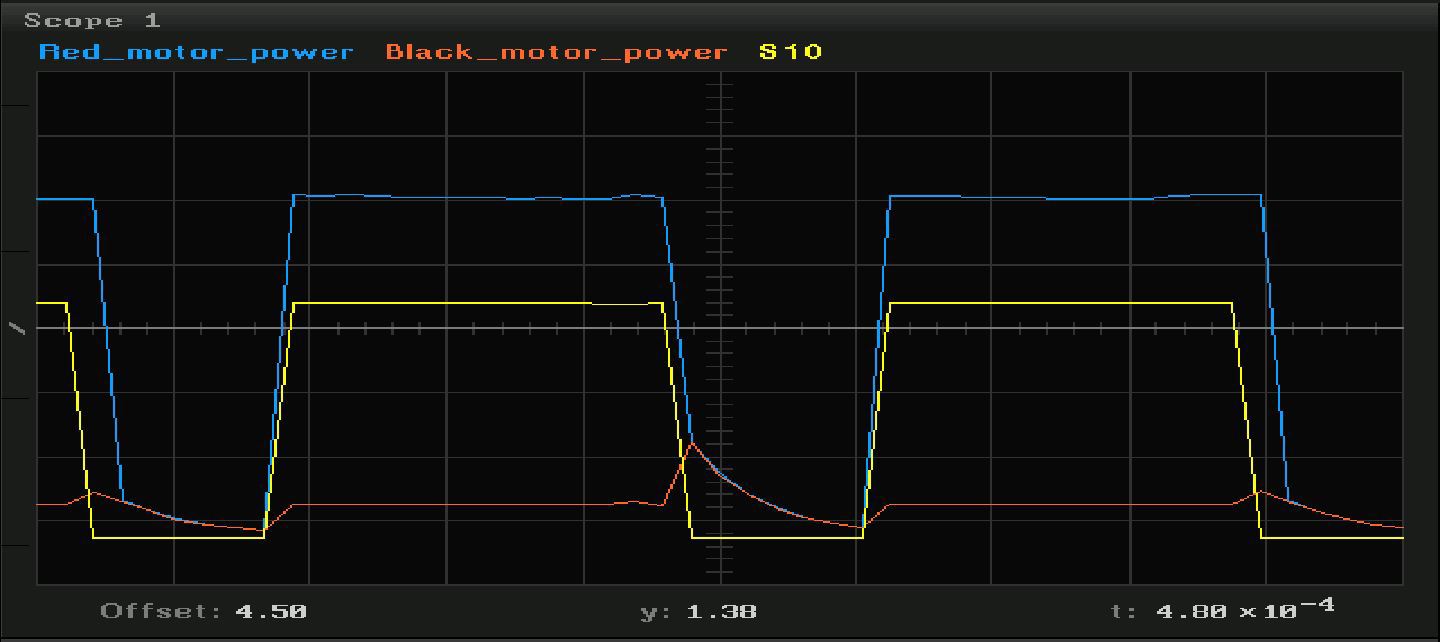
А вот графики при подключенном двигателе в режимах, когда двигатель еще не вращается, и уже вращается:

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

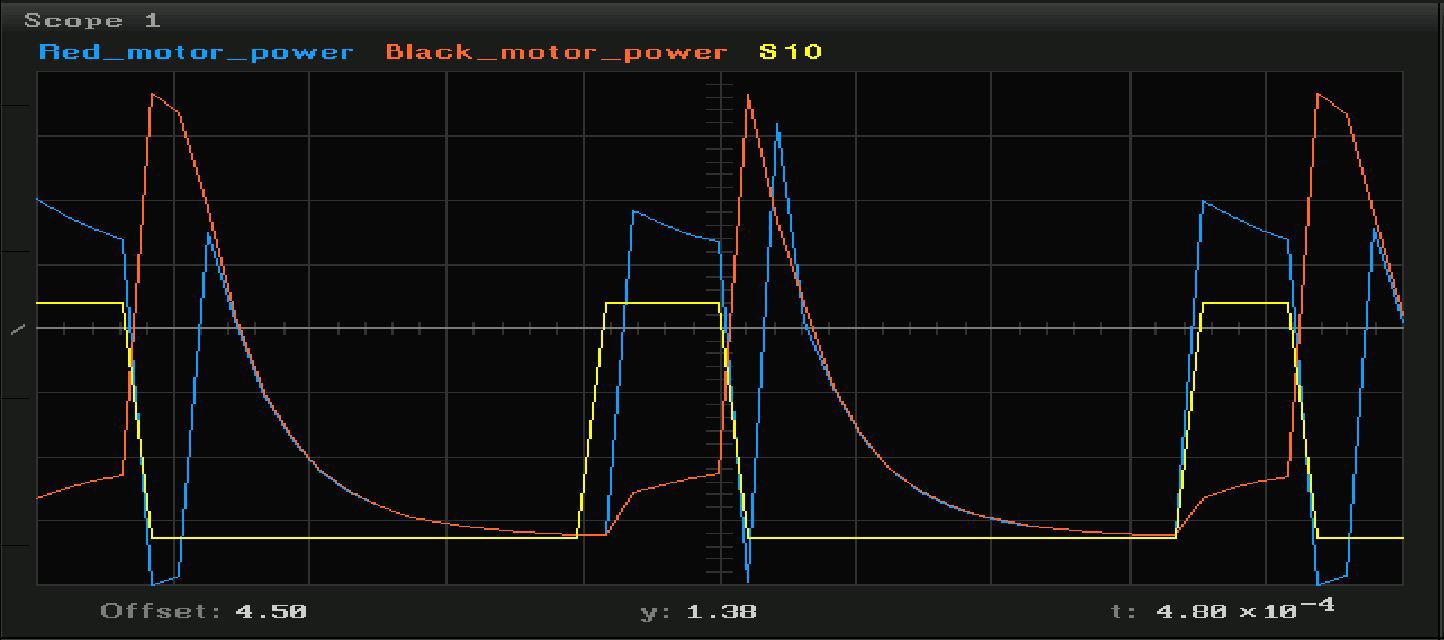
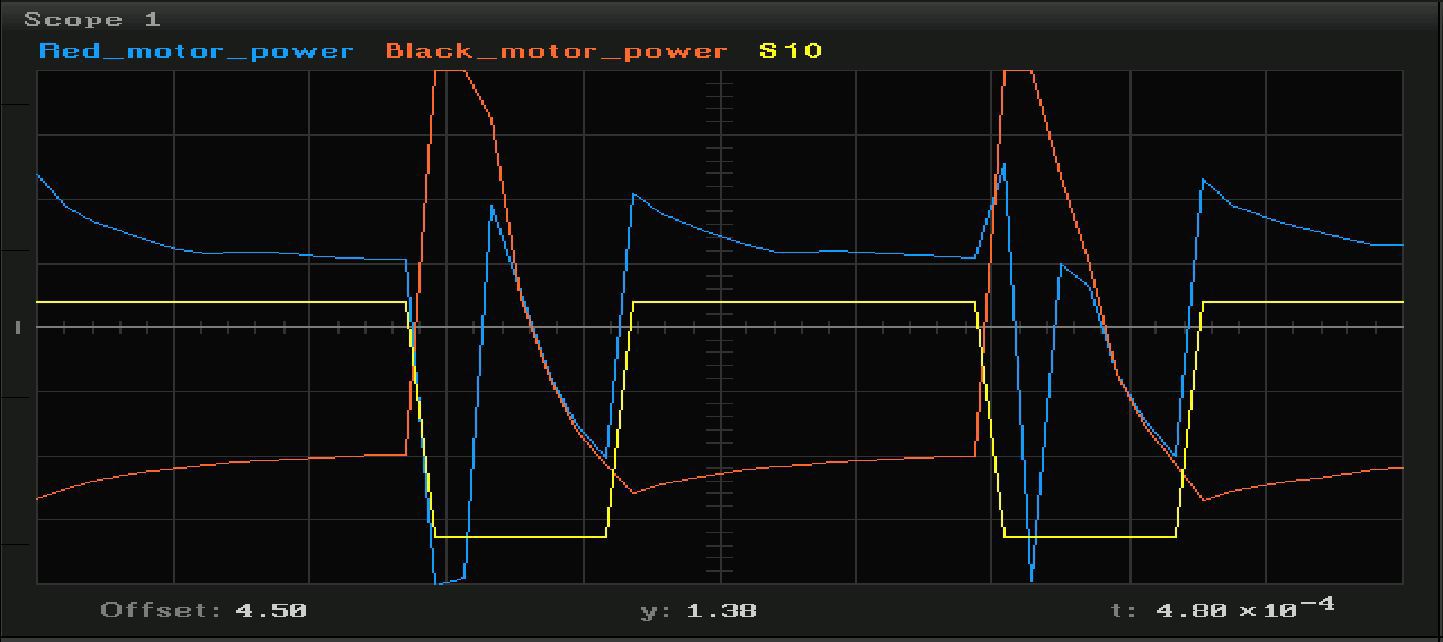
Коммутация индуктивной нагрузки с механическим контактом полупроводниковыми ключами — крайне интересная тема для исследований, но сегодня мы внимания ей уделять не будем. Мы срежем по прямой — будем рассматривать только вход и выход системы, не вникая в физику процессов.

Модели Simulink

На машине реального времени я запускаю вот такую модель:

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

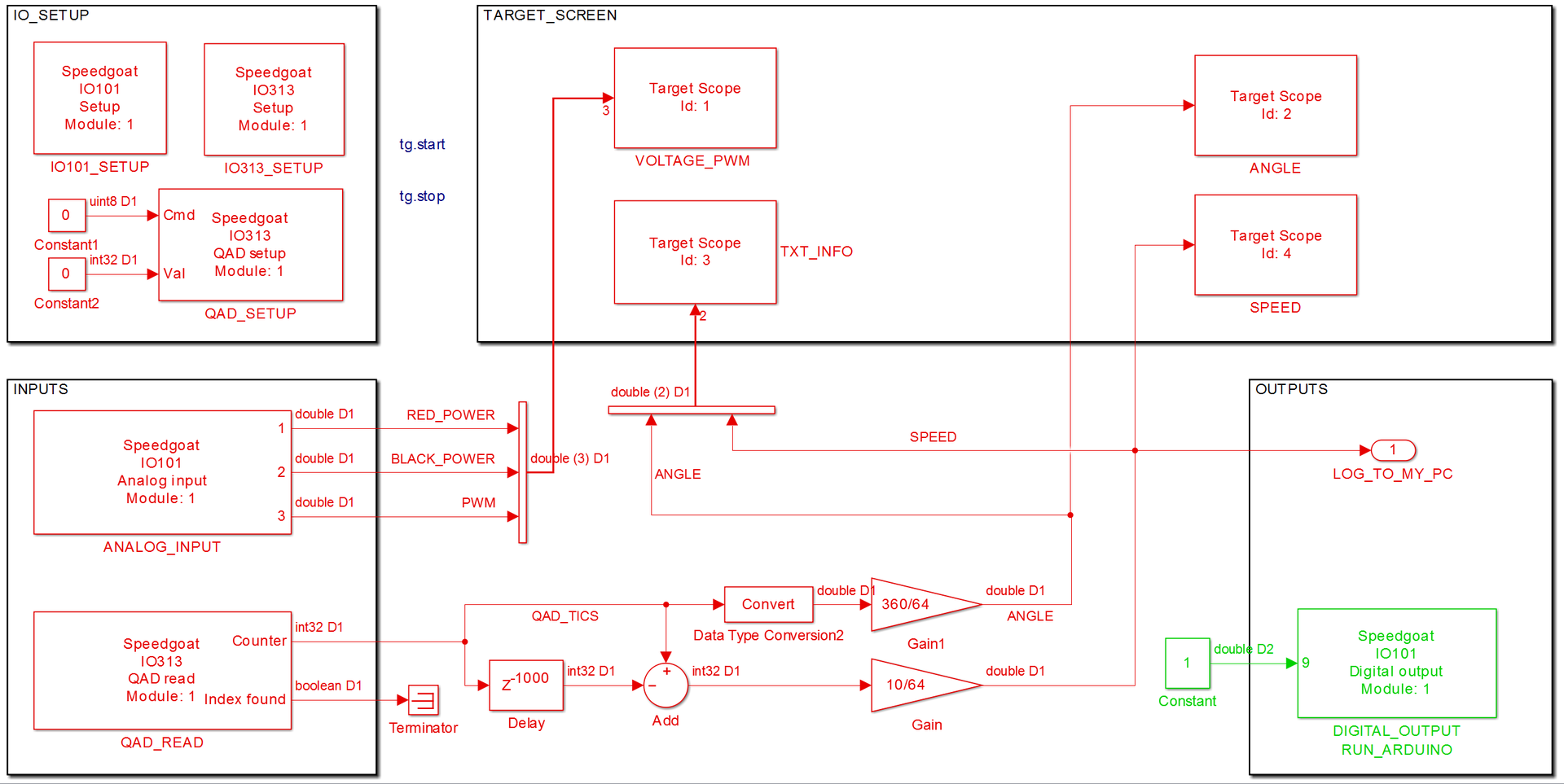
Структура её крайне проста. Есть блоки для входов, выходов, общие настройки плат ввода-вывода, вывод информации на дисплей машинки и простая внутренняя логика пересчета тиков от квадратурного энкодера в угол и скорость.

Модель для получения прошивки под Arduino выглядит следующим образом:

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

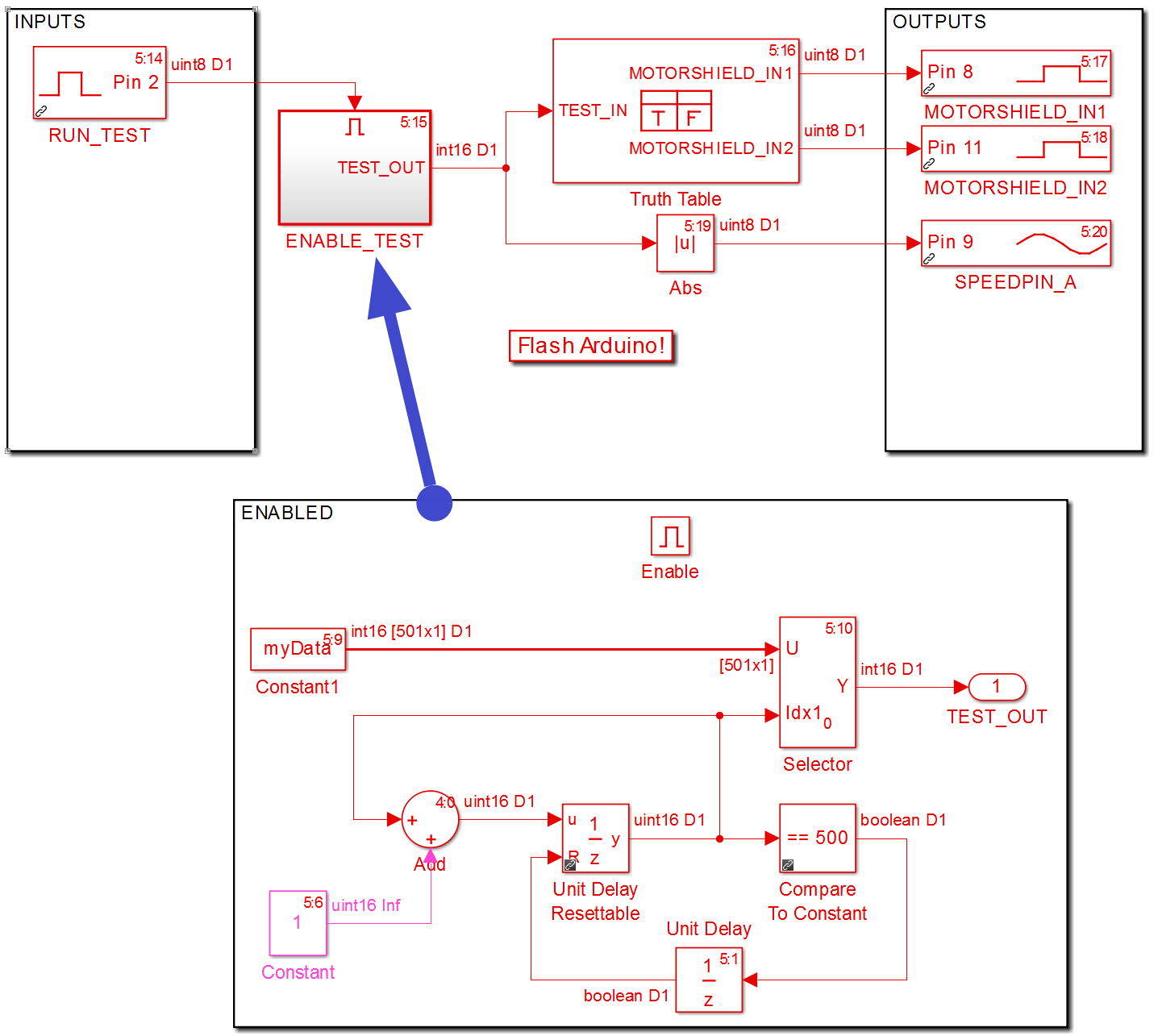
Таблица истинности, которая отслеживает знак сигнала и управляет входами Motor Shield

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

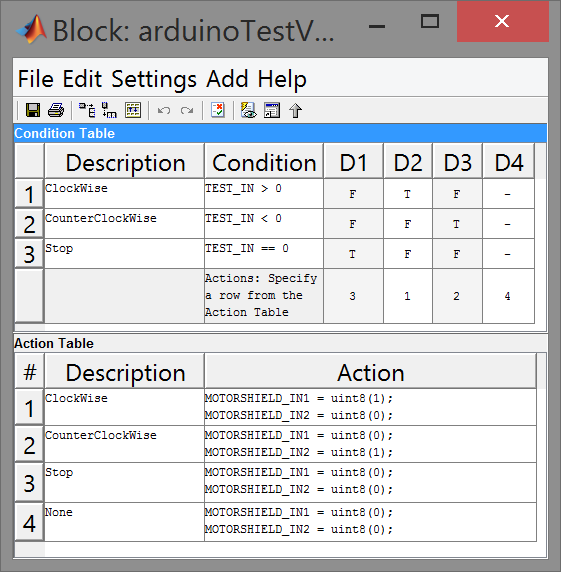
Код алгоритма можно посмотреть под спойлером:

C++

//
// File: arduinoTestVector.cpp
//
// Code generated for Simulink model 'arduinoTestVector'.
//
// Model version                  : 1.229
// Simulink Coder version         : 8.6 (R2014a) 27-Dec-2013
// C/C++ source code generated on : Thu May 22 14:47:55 2014
//
// Target selection: arduino_ec.tlc
// Embedded hardware selection: Atmel->AVR
// Code generation objectives:
//    1. Execution efficiency
//    2. ROM efficiency
//    3. RAM efficiency
// Validation result: Not run
//
#include "arduinoTestVector.h"

// Constant parameters (auto storage)
const ConstParam_arduinoTestVector arduinoTestVector_ConstP = {
  // Expression: myData
  //  Referenced by: '<S1>/Constant1'

  { 0, 1, 3, 4, 5, 6, 8, 9, 10, 11, 13, 14, 15, 17, 18, 19, 20, 22, 23, 24, 26,
    27, 28, 29, 31, 32, 33, 34, 36, 37, 38, 40, 41, 42, 43, 45, 46, 47, 48, 50,
    51, 52, 54, 55, 56, 57, 59, 60, 61, 62, 0, -1, -3, -4, -5, -6, -8, -9, -10,
    -11, -13, -14, -15, -17, -18, -19, -20, -22, -23, -24, -26, -27, -28, -29,
    -31, -32, -33, -34, -36, -37, -38, -40, -41, -42, -43, -45, -46, -47, -48,
    -50, -51, -52, -54, -55, -56, -57, -59, -60, -61, -62, 0, 3, 5, 8, 10, 13,
    15, 18, 20, 23, 26, 28, 31, 33, 36, 38, 41, 43, 46, 48, 51, 54, 56, 59, 61,
    64, 66, 69, 71, 74, 77, 79, 82, 84, 87, 89, 92, 94, 97, 99, 102, 105, 107,
    110, 112, 115, 117, 120, 122, 125, 0, -3, -5, -8, -10, -13, -15, -18, -20,
    -23, -26, -28, -31, -33, -36, -38, -41, -43, -46, -48, -51, -54, -56, -59,
    -61, -64, -66, -69, -71, -74, -77, -79, -82, -84, -87, -89, -92, -94, -97,
    -99, -102, -105, -107, -110, -112, -115, -117, -120, -122, -125, 170, 170,
    170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170,
    170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170,
    170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, 170,
    170, 170, 170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170,
    -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170,
    -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170,
    -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170, -170,
    -170, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
    255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
    255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
    255, 255, 255, 255, 255, 255, -255, -255, -255, -255, -255, -255, -255, -255,
    -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255,
    -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255,
    -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255, -255,
    -255, -255, -255, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85,
    85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85,
    85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, -85, -85,
    -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85,
    -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85, -85,
    -85, -85, -85, -85, -85, -85, -85, -85, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 }
};

// Block signals (auto storage)
BlockIO_arduinoTestVector arduinoTestVector_B;

// Block states (auto storage)
D_Work_arduinoTestVector arduinoTestVector_DWork;

// Model step function
void arduinoTestVector_step(void)
{
  // local block i/o variables
  uint8_T rtb_MOTORSHIELD_IN1;
  uint8_T rtb_MOTORSHIELD_IN2;
  uint8_T rtb_Abs;
  boolean_T aVarTruthTableCondition_1;
  boolean_T aVarTruthTableCondition_2;
  boolean_T aVarTruthTableCondition_3;
  uint16_T rtb_Init;

  // Outputs for Enabled SubSystem: '<Root>/ENABLE_TEST' incorporates:
  //   EnablePort: '<S1>/Enable'

  // S-Function (sfunar_digitalInput): '<Root>/RUN_TEST'
  if (((uint8_T)digitalRead(((uint8_T)2U))) > 0) {
    if (!arduinoTestVector_DWork.ENABLE_TEST_MODE) {
      // InitializeConditions for UnitDelay: '<S1>/Unit Delay'
      arduinoTestVector_DWork.UnitDelay_DSTATE = false;

      // InitializeConditions for UnitDelay: '<S4>/FixPt Unit Delay2'
      arduinoTestVector_DWork.FixPtUnitDelay2_DSTATE = 1U;

      // InitializeConditions for UnitDelay: '<S4>/FixPt Unit Delay1'
      arduinoTestVector_DWork.FixPtUnitDelay1_DSTATE = 0U;
      arduinoTestVector_DWork.ENABLE_TEST_MODE = true;
    }

    // Switch: '<S4>/Init' incorporates:
    //   Constant: '<S4>/Initial Condition'
    //   Logic: '<S4>/FixPt Logical Operator'
    //   UnitDelay: '<S1>/Unit Delay'
    //   UnitDelay: '<S4>/FixPt Unit Delay1'
    //   UnitDelay: '<S4>/FixPt Unit Delay2'

    if (arduinoTestVector_DWork.UnitDelay_DSTATE ||
        (arduinoTestVector_DWork.FixPtUnitDelay2_DSTATE != 0)) {
      rtb_Init = 0U;
    } else {
      rtb_Init = arduinoTestVector_DWork.FixPtUnitDelay1_DSTATE;
    }

    // End of Switch: '<S4>/Init'

    // Selector: '<S1>/Selector' incorporates:
    //   Constant: '<S1>/Constant1'

    arduinoTestVector_B.Selector = arduinoTestVector_ConstP.Constant1_Value
      [(int16_T)rtb_Init];

    // Switch: '<S4>/Reset' incorporates:
    //   UnitDelay: '<S1>/Unit Delay'

    if (arduinoTestVector_DWork.UnitDelay_DSTATE) {
      // Update for UnitDelay: '<S4>/FixPt Unit Delay1' incorporates:
      //   Constant: '<S4>/Initial Condition'

      arduinoTestVector_DWork.FixPtUnitDelay1_DSTATE = 0U;
    } else {
      // Update for UnitDelay: '<S4>/FixPt Unit Delay1' incorporates:
      //   Constant: '<S1>/Constant'
      //   Sum: '<S1>/Add'

      arduinoTestVector_DWork.FixPtUnitDelay1_DSTATE = rtb_Init + 1U;
    }

    // End of Switch: '<S4>/Reset'

    // Update for UnitDelay: '<S1>/Unit Delay' incorporates:
    //   Constant: '<S3>/Constant'
    //   RelationalOperator: '<S3>/Compare'

    arduinoTestVector_DWork.UnitDelay_DSTATE = (rtb_Init == 500U);

    // Update for UnitDelay: '<S4>/FixPt Unit Delay2' incorporates:
    //   Constant: '<S4>/FixPt Constant'

    arduinoTestVector_DWork.FixPtUnitDelay2_DSTATE = 0U;
  } else {
    if (arduinoTestVector_DWork.ENABLE_TEST_MODE) {
      // Disable for Outport: '<S1>/TEST_OUT'
      arduinoTestVector_B.Selector = 0;
      arduinoTestVector_DWork.ENABLE_TEST_MODE = false;
    }
  }

  // End of S-Function (sfunar_digitalInput): '<Root>/RUN_TEST'
  // End of Outputs for SubSystem: '<Root>/ENABLE_TEST'

  // Truth Table: '<Root>/Truth Table'
  // Truth Table Function 'Truth Table': '<S2>:1'
  //  ClockWise
  // Condition '#1': '<S2>:1:10'
  aVarTruthTableCondition_1 = (arduinoTestVector_B.Selector > 0);

  //  CounterClockWise
  // Condition '#2': '<S2>:1:14'
  aVarTruthTableCondition_2 = (arduinoTestVector_B.Selector < 0);

  //  Stop
  // Condition '#3': '<S2>:1:18'
  aVarTruthTableCondition_3 = (arduinoTestVector_B.Selector == 0);
  if ((!aVarTruthTableCondition_1) && (!aVarTruthTableCondition_2) &&
      aVarTruthTableCondition_3) {
    // Decision 'D1': '<S2>:1:20'
    //  Stop
    // Action '3': '<S2>:1:48'
    rtb_MOTORSHIELD_IN1 = 0U;

    // Action '3': '<S2>:1:49'
    rtb_MOTORSHIELD_IN2 = 0U;
  } else {
    // Decision 'D2': '<S2>:1:20'
    if (aVarTruthTableCondition_1 && (!aVarTruthTableCondition_2) &&
        (!aVarTruthTableCondition_3)) {
      // Decision 'D2': '<S2>:1:22'
      //  ClockWise
      // Action '1': '<S2>:1:34'
      rtb_MOTORSHIELD_IN1 = 1U;

      // Action '1': '<S2>:1:35'
      rtb_MOTORSHIELD_IN2 = 0U;
    } else {
      // Decision 'D3': '<S2>:1:22'
      if ((!aVarTruthTableCondition_1) && aVarTruthTableCondition_2 &&
          (!aVarTruthTableCondition_3)) {
        // Decision 'D3': '<S2>:1:24'
        //  CounterClockWise
        // Action '2': '<S2>:1:41'
        rtb_MOTORSHIELD_IN1 = 0U;

        // Action '2': '<S2>:1:42'
        rtb_MOTORSHIELD_IN2 = 1U;
      } else {
        // Decision 'D4': '<S2>:1:24'
        // Decision 'D4': '<S2>:1:26'
        //  Default
        //  None
        // Action '4': '<S2>:1:55'
        rtb_MOTORSHIELD_IN1 = 0U;

        // Action '4': '<S2>:1:56'
        rtb_MOTORSHIELD_IN2 = 0U;
      }
    }
  }

  // End of Truth Table: '<Root>/Truth Table'

  // S-Function (sfunar_digitalOutput): '<Root>/MOTORSHIELD_IN1'
  digitalWrite(((uint8_T)8U), rtb_MOTORSHIELD_IN1);

  // S-Function (sfunar_digitalOutput): '<Root>/MOTORSHIELD_IN2'
  digitalWrite(((uint8_T)11U), rtb_MOTORSHIELD_IN2);

  // Abs: '<Root>/Abs'
  if (arduinoTestVector_B.Selector < 0) {
    rtb_Abs = (uint8_T)-arduinoTestVector_B.Selector;
  } else {
    rtb_Abs = (uint8_T)arduinoTestVector_B.Selector;
  }

  // End of Abs: '<Root>/Abs'

  // S-Function (sfunar_analogOutput): '<Root>/SPEEDPIN_A'
  analogWrite(((uint8_T)9U), rtb_Abs);
}

// Model initialize function
void arduinoTestVector_initialize(void)
{
  // Registration code

  // block I/O
  (void) memset(((void *) &arduinoTestVector_B), 0,
                sizeof(BlockIO_arduinoTestVector));

  // states (dwork)
  (void) memset((void *)&arduinoTestVector_DWork, 0,
                sizeof(D_Work_arduinoTestVector));

  // S-Function (sfunar_digitalInput): <Root>/RUN_TEST
  pinMode(((uint8_T)2U), INPUT);

  // InitializeConditions for Enabled SubSystem: '<Root>/ENABLE_TEST'
  // InitializeConditions for UnitDelay: '<S1>/Unit Delay'
  arduinoTestVector_DWork.UnitDelay_DSTATE = false;

  // InitializeConditions for UnitDelay: '<S4>/FixPt Unit Delay2'
  arduinoTestVector_DWork.FixPtUnitDelay2_DSTATE = 1U;

  // InitializeConditions for UnitDelay: '<S4>/FixPt Unit Delay1'
  arduinoTestVector_DWork.FixPtUnitDelay1_DSTATE = 0U;

  // End of InitializeConditions for SubSystem: '<Root>/ENABLE_TEST'

  // S-Function (sfunar_digitalOutput): <Root>/MOTORSHIELD_IN1
  pinMode(((uint8_T)8U), OUTPUT);

  // S-Function (sfunar_digitalOutput): <Root>/MOTORSHIELD_IN2
  pinMode(((uint8_T)11U), OUTPUT);

  // S-Function (sfunar_analogOutput): <Root>/SPEEDPIN_A
  pinMode(((uint8_T)9U), OUTPUT);
}

//
// File trailer for generated code.
//
// [EOF]
//

Весь проект можно скачать здесь.

Модель, которую я буду использовать для проверки результатов:

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

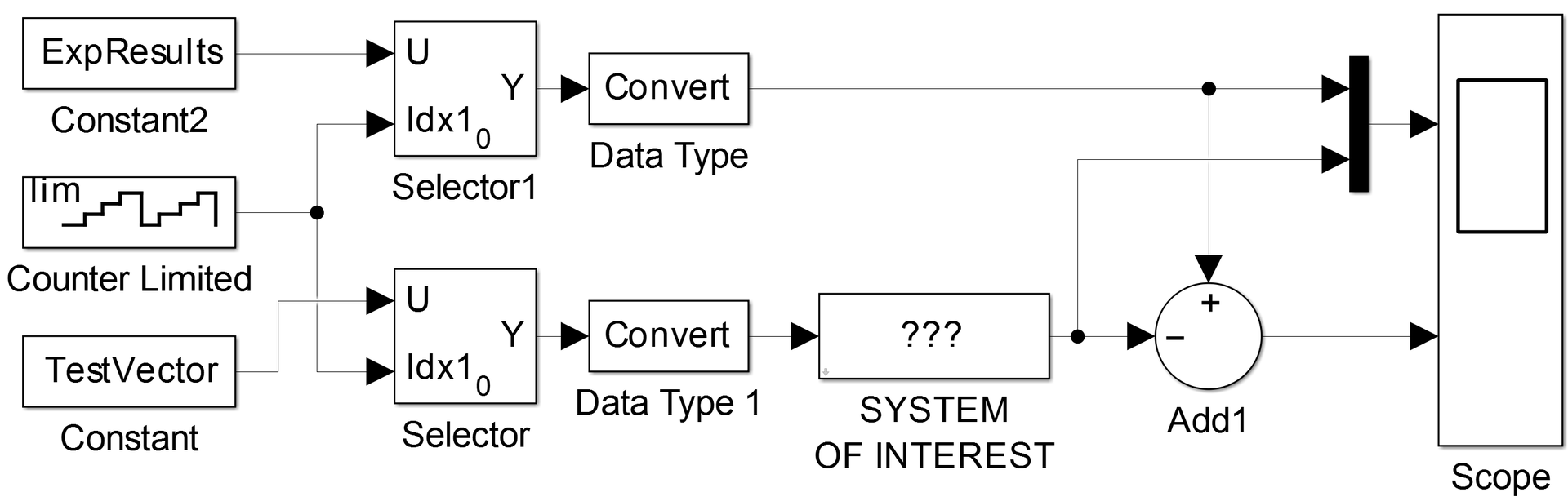
Все модели можно скачать здесь.
«Открыл и запустил» может не сработать, есть нюансы. С вопросами в личку, или в комментарии.

Видео

Результаты

Вот, что получилось в итоге:

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

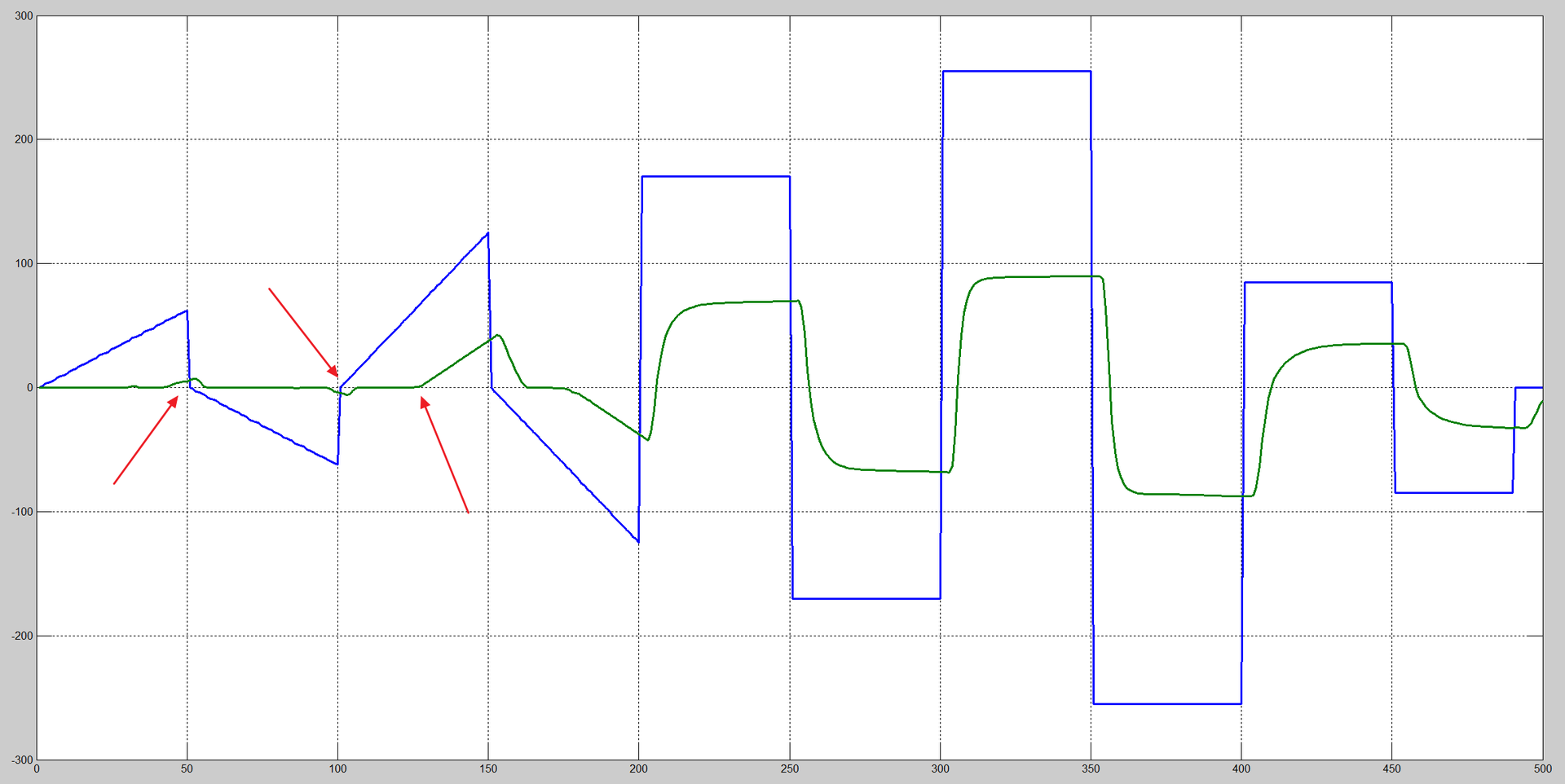
Синий — это входной сигнал с пределами от -255 до +255. В пересчете на вольты будет примерно от -8,5 до 8,5.
Зеленый — скорость вращения вала двигателя.

Видим временную задержку, отсутствие вращения, либо крайне малое вращение при подаче ШИМ менее 25%. Также наблюдаем классический апериодический переходной процесс.

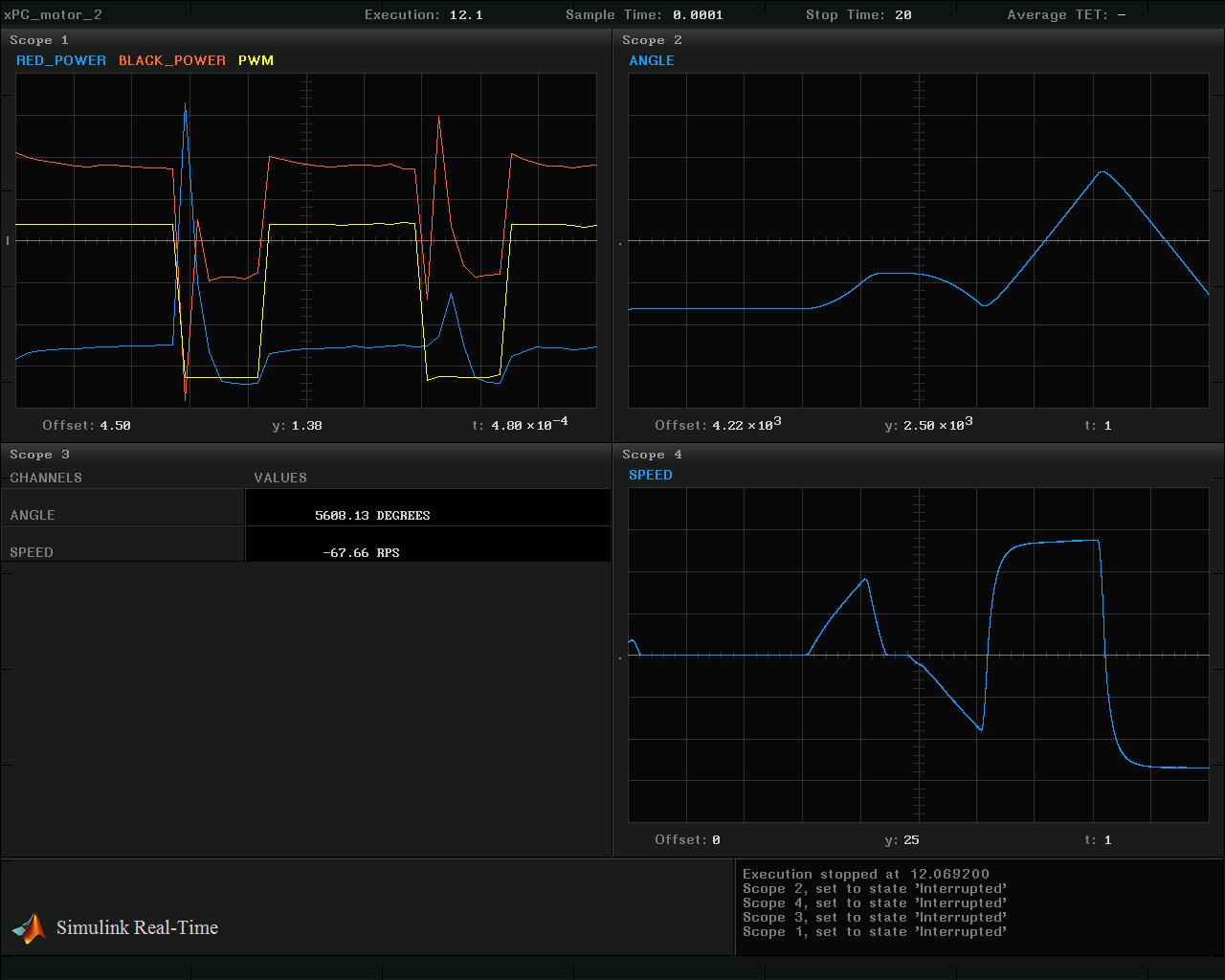
А вот информация, которая выводится во время проведения эксперимента на дисплей, подключенный к машине реального времени:

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

Идентификация

Одна из подсистем, а именно двигатель, может быть описан следующей передаточной функцией:
Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink
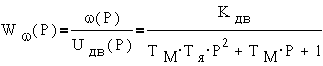
Так нам говорит курс ТАУ, с неё мы и начнем.

В составе MATLAB есть прекрасный инструмент для идентификации систем — System Identification Toolbox. Он доступен как в виде графического интерфейса, так и в виде набора функций, которые можно использовать в скриптах MATLAB. Рассмотрим сперва работу в графическом интерфейсе.

Импортируем данные, полученные в ходе эксперимента и тестовое воздействие:
Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

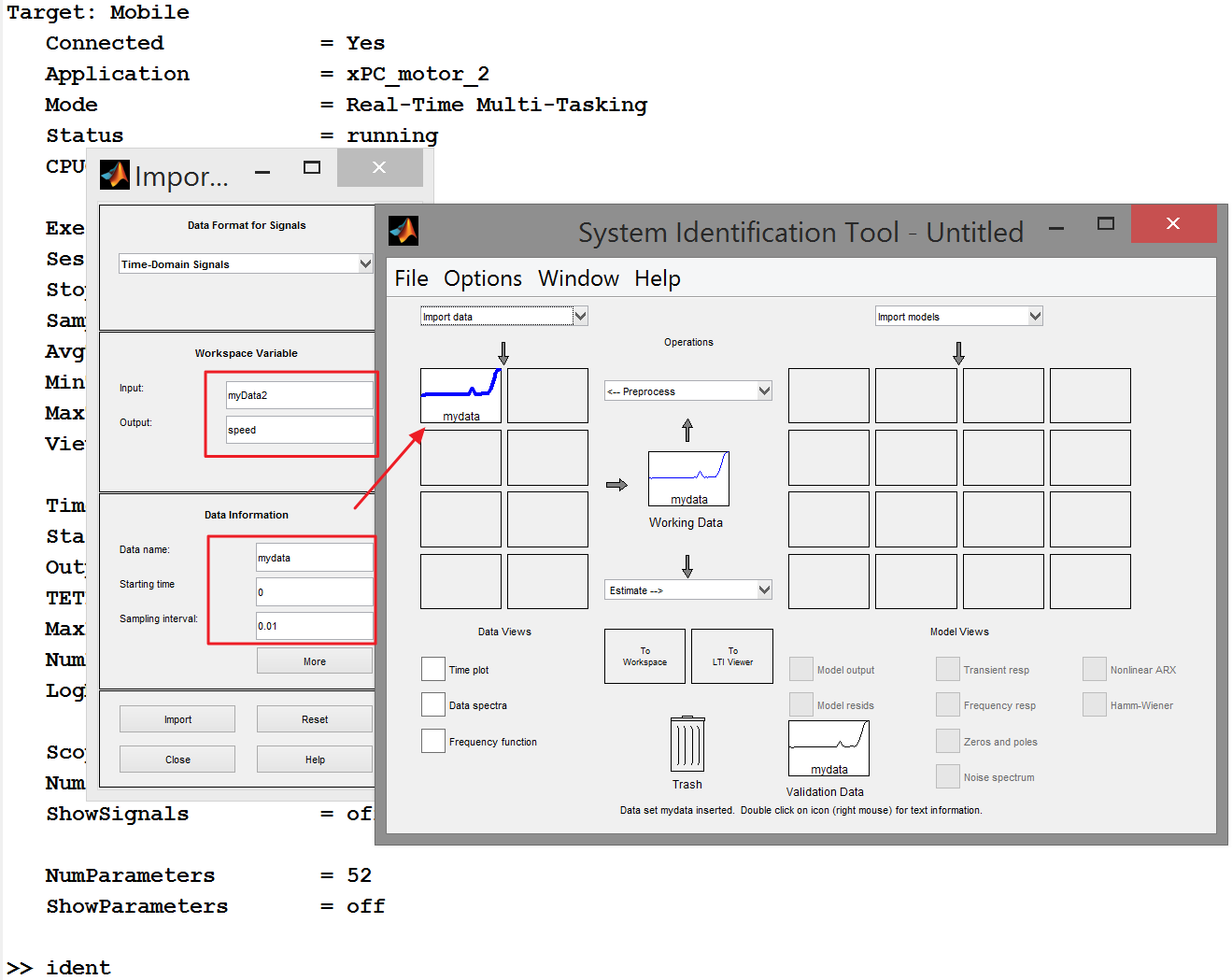
После импорта нам становятся доступны инструменты предварительной обработки данных. Мы имеем возможность, например, разделить массивы данных на две части — для идентификации и отдельно для верификации. Но это для более сложных случаев, давайте же скорее перейдем к делу!

Выбираем из выпадающего списка «Estimate» пункт Transfer Function Models.

Получаем передаточную функцию:
Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

Давайте сравним поведение полученной функции и системы:
Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

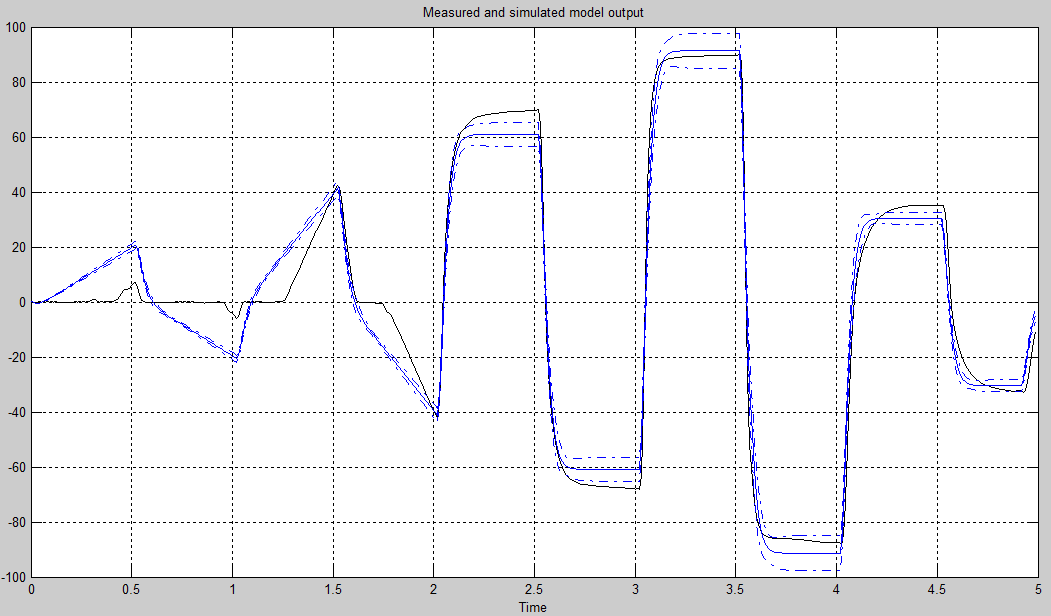
Синим отображен отклик передаточной функции на исходный тестовый вектор. Видно, что данную функцию можно использовать как модель исходной системы только в режиме старт-стоп. И не удивительно — нелинейное поведение, которое присутствует в системе, не может быть описано таким способом.

Продвигаемся дальше, используем шаблон модели Хаммерштейна-Винера, которая дает возможность описывать нелинейное поведение системы:

Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

В качестве входной нелинейности выберем Dead Zone — отсутствие реакции системы на входной сигнал менее определенного порогового значения. Такой тип нелинейности должен взять на себя описание трения спокойствия и влияния постоянных магнитов, которое имеет место в системе.
Остальные параметры по умолчанию, жмем Estimate.

Сравниваем полученный результат с экспериментальными данными:
Модельно ориентированное проектирование на коленке, идентификация систем в MATLAB/Simulink

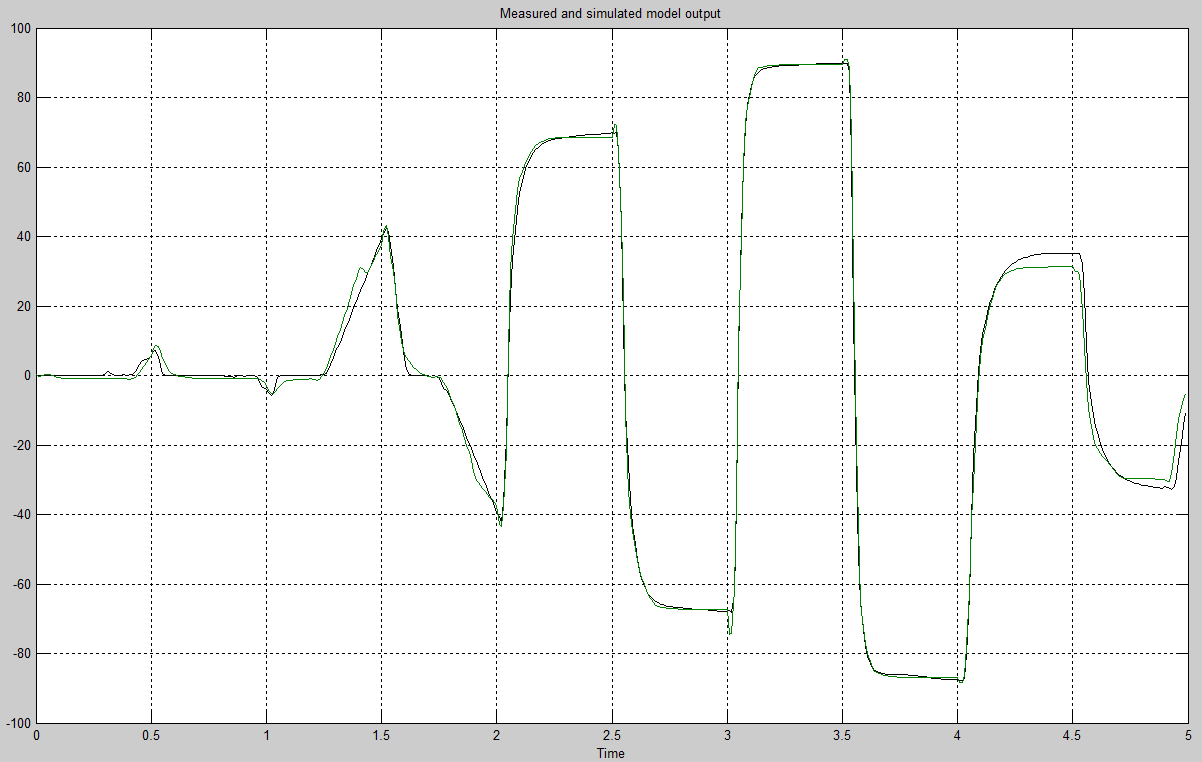
Выглядит гораздо лучше! Не идеально — заметно некоторое аномальное поведение, но мы ведь только слегка коснулись идентификации нелинейных систем.

Теперь нам остается только экспортировать данную модель в Simulink, где мы можем приступить к разработке системы управления. Но об этом в следующем топике!

Благодарю за внимание, надеюсь было интересно?
И еще раз благодарю за ответы на небольшой опрос:

Автор: slovak

Источник

Информация

Обсуждаемое

Рекомендуем