 Этой статьёй я хотел бы продолжить серию своих публикаций о модели квантовых вычислений, которую я начал кратким введением в вопрос об обратимости вычислительных процессов (см. «Слово малое об обратимых вычислениях»). Сегодня я предлагаю вам, уважаемые читатели, рассмотреть один из простейших квантовых алгоритмов, который показывает повышение эффективности по сравнению с классической вычислительной моделью. Я говорю об алгоритме Дойча — в статье описывается именно этот алгоритм в своей первоначальной формулировке. Однако кроме всего прочего для иллюстрации подхода и самого алгоритма используется язык программирования Haskell.
Этой статьёй я хотел бы продолжить серию своих публикаций о модели квантовых вычислений, которую я начал кратким введением в вопрос об обратимости вычислительных процессов (см. «Слово малое об обратимых вычислениях»). Сегодня я предлагаю вам, уважаемые читатели, рассмотреть один из простейших квантовых алгоритмов, который показывает повышение эффективности по сравнению с классической вычислительной моделью. Я говорю об алгоритме Дойча — в статье описывается именно этот алгоритм в своей первоначальной формулировке. Однако кроме всего прочего для иллюстрации подхода и самого алгоритма используется язык программирования Haskell.
В этой статье вы кратко прочтёте об основах модели квантовых вычислений, увидите сравнение классической и квантовой реализации алгоритма Дойча, а также, наконец, поймёте саму суть квантовых вычислений. Так что если кто-то заинтересовался этим вопросом — добро пожаловать под кат.
Немного истории и теории
В 1985 году Давид Дойч разработал один из первых квантовых алгоритмов, который в последствии был признан «базовым» алгоритмом в рамках модели квантовых вычислений. Алгоритм показывает двукратное увеличение эффективности по сравнению с классическими вычислениями при выполнении программы для решения несколько странной задачи. Тем не менее, несмотря на малую степень применимости этой задачи, алгоритм показателен, так что он рассматривается и упоминается во всех книгах, в которых только краем затрагивается вопрос о квантовых вычислениях.
Пусть есть некоторая функция f, которая получает на вход один бит и возвращает один бит. Честно говоря, всего таких функций может быть ровно 4:
| № | Функция | Обозначение | Тип | Определение на языке Haskell |
| 1 | f1(0) = 0 f1(1) = 0 |
0 | Константная |
|
| 2 | f2(0) = 1 f2(1) = 1 |
1 | Константная |
|
| 3 | f3(0) = 0 f3(1) = 1 |
id | Сбалансированная |
|
| 4 | f4(0) = 1 f4(1) = 0 |
not | Сбалансированная |
|
Задачей, которую решал Дойч, было определение того, является ли поданная на вход алгоритма функция константной или сбалансированной. Как это сделать? Очевидно, что в классической вычислительной модели необходимо просто два раза вызвать функцию f, после чего сравнить результаты. Если они получаются равными, то функция константна, а если нет, то сбалансирована. Вряд ли можно умудриться решить эту задачу при помощи одного вызова функции. Следующая таблица показывает постоянную неоднозначность в определении типа функции, если пытаться определить её тип только при помощи одного вызова:
| 0 | 1 | |
| 0 | f1 | f3 | f2 | f4 |
| 1 | f1 | f4 | f2 | f3 |
В первом столбце этой таблицы указаны варианты входных значений, а в первой строке — варианты выходных значений. В ячейках показаны функции, которые возвращают такое-то значение на таком-то аргументе. То есть, функции f1 и f3 возвращают 0, если получают на вход 0, ну и т. д. Поскольку в каждой ячейке таблицы имеется по две функции, решить задачу Дойча за один вызов в классической вычислительной модели невозможно.
Другое дело — модель квантовых вычислений. Здесь можно распознать тип заданной функции при помощи единственного её вызова. Это происходит от того, что имеет место так называемый квантовый параллелизм, когда функция одновременно вызывается на всех возможных значениях своих входных параметров.
Поскольку в модели квантовых вычислений используются не биты, а кубиты, которые могут находиться в произвольной линейной суперпозиции квантовых состояний, сама функция f здесь должна иметь иной вид, чем в классической модели. Она должна быть преобразована в так называемый квантовый оракул, то есть некоторое унитарное преобразование (матрицу определённого вида), которое на входных кубитах работает так же, как и изначальная функция f.
Сама модель квантовых вычислений представляет собой, если очень кратко и наивно, последовательное умножение матриц на векторы, где векторы представляют собой кубиты, а матрицы — унитарные преобразования. Квантовые алгоритмы чаще всего описываются при помощи схем, на которых кубиты показаны при помощи горизонтальных линий, входящих и выходящих из прямоугольников, которые представляют унитарные преобразования (гейты). Внутри прямоугольника ставится обозначение унитарного преобразования. Ну и ещё может быть специальная операция «измерение», которая преобразует кубит в классический бит. Эта операция обозначается в виде пиктограммы измерительного прибора.
Собственно, вот квантовая схема алгоритма Дойча:

Что мы на ней видим? В алгоритме используется два кубита — один основной и второй вспомогательный, оба находятся в начальном состоянии. Прежде всего, вспомогательный кубит подвергается действию гейта X, квантового аналога операции НЕ. После действия этого гейта вспомогательный кубит переходит в состояние |1>. Далее оба кубита одновременно подвергаются действию гейта Адамара H, который переводит кубиты из базисных квантовых состояний в равновероятностные суперпозиции и обратно (он поворачивает кубиты в двумерном гильбертовом пространстве на 45 градусов, если быть откровенным — ниже будет дано точное определение этого гейта в терминах языка Haskell). Теперь настаёт время вызова функции f, которая преобразована в квантовый оракул. После этого вызова (единственного) первый кубит снова подвергается действию гейта Адамара (а второй нам больше не нужен, ибо он был вспомогательным), после чего измеряется. И тут есть две возможности. Если после измерения мы получаем в результате значение 0, то функция константна, а если 1, то, соответственно, сбалансирована.
Это всё несколько странно, и может показаться отчасти магическим, но на самом деле ничего странного и магического тут нет. Всё дело именно в квантовом параллелизме и преобразовании функции в квантовый оракул. Вся магия скрыта здесь, и далее мы рассмотрим, как так получается.
Классический вариант
Для того чтобы понять смысл всей этой задумки, резонно рассмотреть классическую реализацию алгоритма. Как было показано в предыдущем разделе, необходимо сделать ровно два вызова заданной функции, чтобы понять, является ли она константной или сбалансированной. Давайте посмотрим на это в коде.
Перво-наперво реализуем сами функции. Они будут работать на множестве целых чисел Integer, но мы будем использовать только два значения из этого множества — 0 и 1. Это сделано для того, чтобы не морочиться с большим количеством определений и сопоставлений с образцами, что вне всяких сомнений было бы при использовании либо типа Bool, либо какого-то специально определённого для задачи типа. Так что определения этих функций следующие:
f1 :: Integer -> Integer
f1 _ = 0
f2 :: Integer -> Integer
f2 _ = 1
f3 :: Integer -> Integer
f3 = id
f4 :: Integer -> Integer
f4 x = (x + 1) `mod` 2Собственно, реализация функции для решения задачи Дойча — дело абсолютно простое. Сделаем её такой, чтобы она выводила на экран результат своих измерений в виде строки:
deutsch :: (Integer -> Integer) -> IO ()
deutsch f = putStrLn (if f 0 == f 1
then "Функция константна."
else "Функция сбалансирована.")Здесь имеются два вызова заданной функции, как и было обещано. Ну и для полноты реализации можно написать специальную функцию для проверки работы ранее определённой:
testDeutsch :: IO ()
testDeutsch = mapM_ deutsch [f1, f2, f3, f4]Если её запустить, то в консоли интерпретатора будет выведено:
> testDeutsch
Функция константна.
Функция константна.
Функция сбалансирована.
Функция сбалансирована.Что и требовалось…
Подготовка к реализации
Прежде чем реализовать сам алгоритм, необходимо определить довольно большой набор вспомогательных программных сущностей, которые помогут в реализации. Прежде всего это два синонима типов, которые будут описывать векторы и матрицы. Для этих целей больше пригодилась бы какая-либо специальная библиотека с определением всего необходимого для линейной алгебры, но сейчас мы хотим быстро реализовать алгоритм, что называется, «на коленках», чтобы продемонстрировать сам алгоритм и возможности по его выражению на языке Haskell.
Итак, два синонима:
type Vector a = [a]
type Matrix a = [Vector a]Как видно, вектор — это просто список каких-либо значений, а матрица — это список векторов. Но тут есть нюанс: разработчик всегда сам должен следить за корректностью и соответствием размерностей данных, представляемых при помощи этих двух типов. Например, операция умножения матрицы на вектор никак не сможет проверить размерности и гарантировать адекватность своего результата, поэтому именно на разработчика возлагается почётная обязанность контролировать длины списков.
Итак, кубиты будут представляться в виде векторов, а унитарные преобразования или гейты — в виде матриц. Эти векторы и матрицы должны быть комплекснозначными, а это значит, что мы должны подключить модуль Data.Complex. Но внешний вид комплексных чисел в языке Haskell довольно громоздок, поэтому резонно определить несколько вспомогательных функций для конструирования комплекснозначных векторов и матриц из тех, в которых содержатся целые числа. Вот эти две функции:
vectorToComplex :: Integral a => Vector a -> Vector (Complex Double)
vectorToComplex = map (i -> fromIntegral i :+ 0.0)
matrixToComplex :: Integral a => Matrix a -> Matrix (Complex Double)
matrixToComplex = map vectorToComplexКак видно из их наименований, первая функция переводит вектор со счётными значениями в комплекснозначный вектор, а вторая функция делает то же самое с матрицами. Ну вот, к примеру, как их можно использовать:
qubitZero :: Vector (Complex Double)
qubitZero = vectorToComplex [1, 0]
qubitOne :: Vector (Complex Double)
qubitOne = vectorToComplex [0, 1]
gateX :: Matrix (Complex Double)
gateX = matrixToComplex [[0, 1],
[1, 0]]
Тут определены кубиты |0> и |1>, а также гейт X, который представляет собой квантовую операцию НЕ. А вот так можно определить гейт H, представляющий собой преобразование Адамара:
gateH :: Matrix (Complex Double)
gateH = ((1/sqrt 2) :+ 0.0) <*> matrixToComplex [[1, 1],
[1, -1]]Ещё нам потребуется функция для связывания нескольких кубитов в один квантовый регистр. По своей сути эта функция реализует тензорное произведение на векторах, которые представляют кубиты. Написать её на языке Haskell — одно удовольствие:
entangle :: Num a => Vector a -> Vector a -> Vector a
entangle q1 q2 = [qs1 * qs2 | qs1 <- q1, qs2 <- q2]
Эта функция связывает два переданных её на вход кубита. Например, если ей дать кубиты |0> и |0>, то на выходе будет кубит |00>. Само собой разумеется, что тут имеет место векторное представление, поэтому кубит |0> представляется как [1, 0], а кубит |00> — как [1, 0, 0, 0]. Остальные пары базисных кубитов вдумчивый читатель сможет проверить самостоятельно, равно как и проверить кубиты в суперпозициях базисных квантовых состояний.
Теперь определим набор операторов для проведения квантовых вычислений. Это будут операторы для умножения матрицы на вектор, а также другие важные операторы.
apply :: Num a => Matrix a -> Vector a -> Vector a
apply m v = map (sum . zipWith (*) v) m
(|>) :: Num a => Vector a -> Matrix a -> Vector a
(|>) = flip apply
Функция apply применяет заданный гейт к заданному кубиту. Результатом её работы будет новый кубит, то есть вектор. По своей сути это просто произведение матрицы на вектор. Ну а оператор (|>) предназначен исключительно для красоты записи. Это та же функция apply, но с аргументами, переставленными местами — на первом месте вектор, а на втором матрица. К тому же, это инфиксный оператор, поэтому применение гейта к кубиту можно записывать как «qubitZero |> gateX», что вполне соответствует схемной записи квантовых алгоритмов.
(<*>) :: Num a => a -> Matrix a -> Matrix a
c <*> m = map (map (c *)) m
Это оператор для умножения числа на матрицу. В результате получается матрица, все элементы которой равняются произведению элементов изначальной матрицы на заданное число. Использование этого оператора мы уже наблюдали в определении гейта Адамара gateH. И, наконец, последнее в этом разделе определение оператора:
(<+>) :: Num a => Matrix a -> Matrix a -> Matrix a
m1 <+> m2 = concatMap collateRows $ groups n [c <*> m2 | c <- concat m1]
where
n = length $ head m1
groups :: Int -> [a] -> [[a]]
groups i s | null s = []
| otherwise = let (h, t) = splitAt i s
in h : groups i t
collateRows :: [Matrix a] -> Matrix a
collateRows = map concat . transposeЭто самое сложное определение из всего разрабатываемого модуля. Этот оператор осуществляет тензорное произведение двух матриц, и из матриц n x m и p x q делает матрицу (n * p) x (m * q). Элементы матрицы-результата вычисляются по правилам тензорного произведения для матриц. Этот оператор потребуется при создании гейтов для двух кубитов из однокубитных гейтов.
Реализация квантового алгоритма
Теперь необходимо реализовать квантовые оракулы для четырёх функций, которые перечислены в таблице в начале статьи. В модели квантовых вычислений оракулом называется специального вида гейт, который осуществляет вычисление заданной функции. Поскольку у нас здесь на схеме входных кубитов два, то эти гейты оракулов будут представлять собой матрицы размера 4 x 4. Чтобы их создать, необходимо немного заняться квантовой схемотехникой.
Нам будет необходимо спроектировать четыре гейта, которые осуществляют следующее унитарное преобразование:
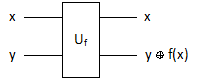
Рассмотрим первую функцию, которая является константной и на любом своём аргументе возвращает 0. Для построения гейта необходимо воспользоваться таблицей следующего вида:
| x | y | f x | y + f x | Преобразование |
| 0 | 0 | 0 | 0 | |00> -> |00> |
| 0 | 1 | 0 | 1 | |01> -> |01> |
| 1 | 0 | 0 | 0 | |10> -> |10> |
| 1 | 1 | 0 | 1 | |11> -> |11> |
Для того чтобы прочитать столбец «Преобразование», необходимо помнить, что в кубите слева от стрелки на первой позиции стоит значение x, а на второй — y. В кубите справа от стрелки на первой позиции опять стоит значение x, а на второй — y + f x. Понятно, что в данном случае унитарное преобразование задаётся единичной матрицей размера 4 x 4.
Абсолютно так же можно построить матрицу гейта для второй функции, которая является константной и всегда возвращает значение 1. Снова составим вспомогательную таблицу, которая поможет затем нарисовать унитарную матрицу, представляющую гейт. Вот она:
| x | y | f x | y + f x | Преобразование |
| 0 | 0 | 0 | 0 | |00> -> |01> |
| 0 | 1 | 0 | 1 | |01> -> |00> |
| 1 | 0 | 0 | 0 | |10> -> |11> |
| 1 | 1 | 0 | 1 | |11> -> |10> |
Другими словами, данное унитарное преобразование должно всегда применять операцию отрицания ко второму кубиту, независимо от значения первого кубита. Матрица такого преобразования выглядит следующим образом:
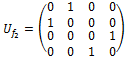
Вдумчивый читатель уже наверняка понял, как выглядят матрицы для третьей и четвёртой функции. В любом случае, их построение будет хорошей тренировкой понимания всего прочитанного к настоящему моменту материала. Ну а здесь мы просто покажем исходный код для представления всех оракулов:
f1' :: Matrix (Complex Double)
f1' = matrixToComplex [[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]
f2' :: Matrix (Complex Double)
f2' = matrixToComplex [[0, 1, 0, 0],
[1, 0, 0, 0],
[0, 0, 0, 1],
[0, 0, 1, 0]]
f3' :: Matrix (Complex Double)
f3' = matrixToComplex [[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 0, 1],
[0, 0, 1, 0]]
f4' :: Matrix (Complex Double)
f4' = matrixToComplex [[0, 1, 0, 0],
[1, 0, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]Дело осталось за малым. Теперь надо реализовать квантовый вариант алгоритма, и, принимая во внимание все реализованные к настоящему моменты вспомогательные программные сущности. Вот функция:
deutsch' :: Matrix (Complex Double) -> IO ()
deutsch' f = do let (result:_) = measure circuit
case result of
'0' -> putStrLn "Функция f константна."
'1' -> putStrLn "Функция f сбалансирована."
_ -> return ()
where
gateH2 = gateH <+> gateH
circuit = entangle qubitZero (qubitZero |> gateX) |> gateH2
|> f
|> gateH2
measure q = let result = map (c -> round (realPart (c * conjugate c))) q
in case result of
[0, 1, 0, 0] -> "01"
[0, 0, 0, 1] -> "11"
_ -> "??"
Тут есть один нюанс. Локально определённая функция measure выполняет не совсем те измерения, которые приняты в рамках модели квантовых вычислений. В данном случае эта локальная функция вычисляет модуль квадратов амплитуд всех квантовых состояний, входящих в состав квантового регистра. Затем при помощи сравнения с двумя предопределёнными списками возвращается та или иная строка, описывающая состояние двух кубитов. Третий образец выражения case сделан исключительно для корректности кода; управление никогда в него не попадёт.
По алгоритму Дойча после измерения нас интересует только первый кубит, поэтому в основной функции берётся именно он и сравнивается с 0 или 1 (третий образец опять представлен для корректности). И если измерение вернуло 0, то функция константна, а если 1, то сбалансирована.
Теперь стоит обратиться к локальному определению circuit. Это и есть реализация квантовой схемы алгоритма Дойча, которая дважды приведена на диаграммах в этой статье. Как видно, при помощи реализованного оператора (|>) квантовая схема очень приятно перекладывается на код на языке Haskell. Что тут делается? Для начала кубит |0> (qubitZero) пропускается через гейт X (gateX), потом результат скрещивается с кубитом |0>, в результате чего получается квантовый регистр |01>. Далее этот квантовый регистр пропускается через двойной гейт Адамара, далее через оракул f, и опять через двойной гейт Адамара. Как видно, квантовый оракул, представляющий исследуемую функцию, задействуется только один раз. В этом и есть удивительная особенность квантового алгоритма Дойча.
Наконец, осталось написать функцию для проверки алгоритма, как это было сделано для классической реализации. В общем-то, тут будет всё то же самое. Вот код:
testDeutsch' :: IO ()
testDeutsch' = mapM_ deutsch' [f1', f2', f3', f4']В результате выполнения этой функции в консоли будет выведено:
> testDeutsch’
Функция константна.
Функция константна.
Функция сбалансирована.
Функция сбалансирована.Что повторно и требовалось…
Заключение
Стороннему наблюдателю это может показаться странным, но квантовый алгоритм Дойча действительно выигрывает в два раза по сравнению с классической версией. Для того чтобы определить тип функции, её действительно можно запустить только один раз. Дело в том, что тут проявляется параллелизм в рамках модели квантовых вычислений, и оказывается, что функция одновременно вычисляет своё значение на всех возможных вариантах значений своего аргумента.
Иной может возразить, что первоначальная функция была преобразована в какую-то матрицу, в которой от изначальной функции ничего не осталось, и именно эта матрица запускается один раз (используется в цепочке произведений матриц), а что там в ней — одному Дойчу известно. Однако это спорный аргумент, поскольку унитарное преобразование, полученное из функции, находится с самой функцией во взаимно-однозначном соответствии. Другое дело, что для использования в рамках модели квантовых вычислений нам действительно надо преобразовать функцию в квантовый оракул, но от этого никуда не деться — такова модель.
Кстати, алгоритм Дойча можно реализовать, что называется, «в железе». Есть физические процессы, например, передача фотонов или других подобных частиц, при помощи которых аналоговым образом можно реализовать этот алгоритм. Первого комментатора, который приведёт здесь схему физической (аналоговой) реализации алгоритма Дойча, ждёт приз. Очень прикольный приз.
Остаётся отметить, что данная статья написана в рамках подготовки к реализации моего проекта по написанию книги «Квантовые вычисления и функциональное программирование». Если вам пришлась по вкусу эта статья, вы могли бы обратить более пристальное внимание на проект. Ну а исходный код к статье всяк может найти здесь.
Автор: Darkus






