В предыдущей части мы описали самые простые свойства формальных нейронов. Проговорили о том, что пороговый сумматор точнее воспроизводит природу единичного спайка, а линейный сумматор позволяет смоделировать ответ нейрона, состоящий из серии импульсов. Показали, что значение на выходе линейного сумматора можно сопоставить с частотой вызванных спайков реального нейрона. Теперь мы посмотрим на основные свойства, которыми обладают такие формальные нейроны.
Фильтр Хебба
Далее мы будем часто обращаться к нейросетевым моделям. В принципе, практически все основные концепции из теории нейронных сетей имеют прямое отношение к строению реального . Человек, сталкиваясь с определенными задачами, придумал множество интересных нейросетевых конструкций. Эволюция, перебирая все возможные нейронные механизмы, отобрала все, что оказалось для нее полезным. Не стоит удивляться, что для очень многих моделей, придуманных человеком, можно найти четкие биологические прототипы. Поскольку наше повествование не ставит целью хоть сколько-либо детальное изложение теории нейронных сетей, мы коснемся только наиболее общих моментов, необходимых для описания основных идей. Для более глубокого понимания я крайне рекомендую обратиться к специальной литературе. По мне лучший учебник по нейронным сетям — это Саймон Хайкин «Нейронные сети. Полный курс» (Хайкин, 2006).
В основе многих нейросетевых моделей лежит хорошо известное правило обучения Хебба. Оно было предложено физиологом Дональдом Хеббом в 1949 году (Hebb, 1949). В немного вольной трактовке оно имеет очень простой смысл: связи нейронов, активирующихся совместно, должны усиливаться, связи нейронов, срабатывающих независимо, должны ослабевать.
Состояние выхода линейного сумматора можно записать:
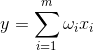
Если мы инициируем начальные значения весов малыми величинами и будем подавать на вход различные образы, то ничто не мешает нам попробовать обучать этот нейрон по правилу Хебба:
где n – дискретный шаг по времени, –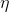 
параметр скорости обучения.
Такой процедурой мы увеличиваем веса тех входов, на которые подается сигнал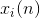 
, но делаем это тем сильнее, чем активнее реакция самого обучаемого нейрона 
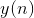. Если нет реакции, то не происходит и обучение.
Правда, такие веса будут неограниченно расти, поэтому для стабилизации можно применить нормировку. Например, поделить на длину вектора, полученного из «новых» синаптических весов.
При таком обучении происходит перераспределение весов между синапсами. Понять суть перераспределения легче, если следить за изменением весов в два приема. Сначала, когда нейрон активен, те синапсы, на которые поступает сигнал, получают добавку. Веса синапсов без сигнала остаются без изменений. Затем общая нормировка уменьшает веса всех синапсов. Но при этом синапсы без сигналов теряют по сравнению со своим предыдущим значением, а синапсы с сигналами перераспределяют между собой эти потери.
Правило Хебба есть не что иное, как реализация метода градиентного спуска по поверхности ошибки. По сути, мы заставляем нейрон подстроиться под подаваемые сигналы, сдвигая каждый раз его веса в сторону, противоположную ошибке, то есть в направлении антиградиента. Чтобы градиентный спуск привел нас к локальному экстремуму, не проскочив его, скорость спуска должна быть достаточно мала. Что в Хеббовском обучении учитывается малостью параметра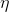 
.
Малость параметра скорости обучения позволяет переписать предыдущую формулу в виде ряда по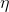 
:
Если отбросить слагаемые второго порядка и выше, то получится правило обучения Ойа (Oja, 1982):
Положительная добавка отвечает за Хеббовское обучение, а отрицательная за общую стабильность. Запись в таком виде позволяет почувствовать, как такое обучение можно реализовать в аналоговой среде без использования вычислений, оперируя только положительными и отрицательными связями.
Так вот, такое крайне простое обучение обладает удивительным свойством. Если мы будем постепенно уменьшать скорость обучения, то веса синапсов обучаемого нейрона сойдутся к таким значениям, что его выход начинает соответствовать первой главной компоненте, которая получилась бы, если бы мы применили к подаваемым данным соответствующие процедуры анализа главных компонент. Такая конструкция называется фильтром Хебба.
Например, подадим на вход нейрона пиксельную картинку, то есть сопоставим каждому синапсу нейрона одну точку изображения. Будем подавать на вход нейрона всего два образа – изображения вертикальных и горизонтальных линий, проходящих через центр. Один шаг обучения – одно изображение, одна линия, либо горизонтальная, либо вертикальная. Если эти изображения усреднить, то получится крест. Но результат обучения не будет похож на усреднение. Это будет одна из линий. Та, которая будет чаще встречаться в подаваемых изображениях. Нейрон выделит не усреднение или пересечение, а те точки, что чаще всего встречаются совместно. Если образы будут более сложными, то результат может быть не столь нагляден. Но это всегда будет именно главная компонента.
Обучение нейрона ведет к тому, что на его весах выделяется (фильтруется) определенный образ. Когда подается новый сигнал, то чем точнее совпадение сигнала и настройки весов, тем выше отклик нейрона. Обученный нейрон можно назвать нейроном-детектором. При этом образ, который описывается его весами, принято называть характерным стимулом.
Главные компоненты
Сама идея метода главных компонент проста и гениальна. Предположим, что у нас есть последовательность событий. Каждое из них мы описываем через его влияние на сенсоры, которыми мы воспринимаем мир. Допустим, что у нас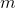 
сенсоров, описывающих 
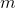признаков . Все события для нас описывается векторами 
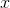размерности 
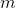. Каждый компонент 
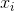такого вектора указывают на значение соответствующего 
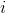-го признака. Все вместе они образуют случайную величину X. Эти события мы можем изобразить в виде точек в 
-мерном пространстве, где осями будут выступать наблюдаемые нами признаки.
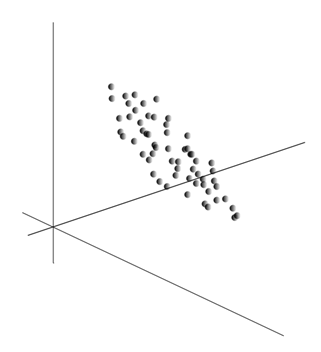
Усреднение значений 
дает математическое ожидание случайной величины X, обозначаемое, как E(X). Если мы отцентрируем данные так, чтобы E(X)=0, то облако точек будет сконцентрировано вокруг начала координат.
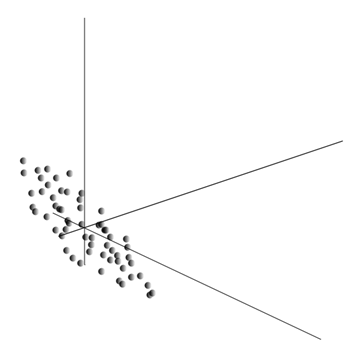
Это облако может оказаться вытянутым в каком-либо направлении. Перепробовав все возможные направления, мы можем найти такое, вдоль которого дисперсия данных будет максимальной.
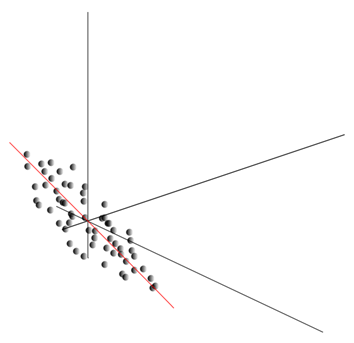
Так вот, такое направление соответствует первой главной компоненте. Сама главная компонента определяется единичным вектором, выходящим из начала координат и совпадающим с этим направлением.
Далее мы можем найти другое направление, перпендикулярное первой компоненте, такое, чтобы вдоль него дисперсия также была максимальной среди всех перпендикулярных направлений. Найдя его, мы получим вторую компоненту. Затем мы можем продолжить поиск, задавшись условием, что искать надо среди направлений, перпендикулярных уже найденным компонентам. Если исходные координаты были линейно независимы, то так мы сможем поступить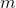 
раз, пока не закончится размерность пространства. Таким образом, мы получим 
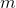взаимоортогональных компонент 
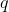, упорядоченных по тому, какой процент дисперсии данных они объясняют.
Естественно, что полученные главные компоненты отражают внутренние закономерности наших данных. Но есть более простые характеристики, также описывающие суть имеющихся закономерностей.
Предположим, что всего у нас n событий. Каждое событие описывается вектором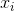 
. Компоненты этого вектора:
Для каждого признака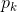 
можно записать, как он проявлял себя в каждом из событий:
Для любых двух признаков, на которых строится описание, можно посчитать величину, показывающую степень их совместного проявления. Эта величина называется ковариацией:
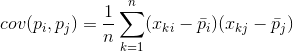
Она показывает, насколько отклонения от среднего значения одного из признаков совпадают по проявлению с аналогичными отклонениями другого признака. Если средние значения признаков равны нулю, то ковариация принимает вид:
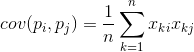
Если скорректировать ковариацию на среднеквадратические отклонения, свойственные признакам, то мы получим линейный коэффициент корреляции, называемый еще коэффициентом корреляции Пирсона:
Коэффициент корреляции обладает замечательным свойством. Он принимает значения от -1 до 1. Причем 1 означает прямую пропорциональность двух величин, а -1 говорит об их обратной линейной зависимости.
Из всех попарных ковариаций признаков можно составить ковариационную матрицу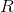 
, которая, как несложно убедиться, есть математическое ожидание произведения 
:
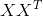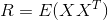
Будем далее полагать, что наши данные отнормированы, то есть имеют единичную дисперсию. В этом случае корреляционная матрица совпадает с ковариационной матрицей.
Так вот оказывается, что для главных компонент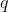 
справедливо:
То есть главные компоненты, или, как еще их называют, факторы являются собственными векторами корреляционной матрицы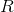 
. Им соответствуют собственные числа 
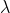. При этом, чем больше собственное число, тем больший процент дисперсии объясняет это фактор.
Зная все главные компоненты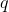 
, для каждого события 
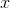, являющегося реализацией X, можно записать его проекции на главные компоненты:
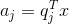
Таким образом, можно представить все исходные события в новых координатах, координатах главных компонент:
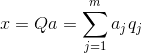
Вообще различают процедуру поиска главных компонент и процедуру нахождения базиса из факторов и его последующее вращение, облегчающее трактовку факторов, но так как эти процедуры идеологически близки и дают похожий результат, будем называть и то и другое факторным анализом.
За достаточно простой процедурой факторного анализа кроется очень глубокий смысл. Дело в том, что если пространство исходных признаков – это наблюдаемое пространство, то факторы – это признаки, которые хотя и описывают свойства окружающего мира, но в общем случае (если не совпадают с наблюдаемыми признаками) являются сущностями скрытыми. То есть формальная процедура факторного анализа позволяет от явлений наблюдаемых перейти к обнаружению явлений, хотя непосредственно и невидимых, но, тем не менее, существующих в окружающем мире.
Можно предположить, что наш активно использует выделение факторов как одну из процедур познания окружающего мира. Выделяя факторы, мы получаем возможность строить новые описания происходящего с нами. Основа этих новых описаний – выраженность в происходящем тех явлений, что соответствуют выделенным факторам.
Немного поясню суть факторов на бытовом уровне. Предположим, вы менеджер по персоналу. К вам приходит множество людей, и относительно каждого вы заполняете определенную форму, куда записываете разные наблюдаемые данные о посетителе. Просмотрев потом свои записи, вы можете обнаружить, что некоторые графы имеют определенную взаимосвязь. Например, стрижка у мужчин будет в среднем короче, чем у женщин. Лысых людей вы, скорее всего, встретите только среди мужчин, а красить губы будут только женщины. Если к анкетным данным применить факторный анализ, то именно пол и окажется одним из факторов, объясняющим сразу несколько закономерностей. Но факторный анализ позволяет найти все факторы, которые объясняют корреляционные зависимости в наборе данных. Это значит, что кроме фактора пола, который мы можем наблюдать, выделятся и другие, в том числе и неявные, ненаблюдаемые факторы. И если пол явным образом будет фигурировать в анкете, то другой важный фактор останется между строк. Оценивая способность людей связано излагать свои мысли, оценивая их карьерную успешность, анализируя их оценки в дипломе и тому подобные признаки, вы придете к выводу, что есть общая оценка интеллекта человека, которая явным образом в анкете не записана, но которая объясняет многие ее пункты. Оценка интеллекта – это и есть скрытый фактор, главная компонента с высоким объясняющим эффектом. Явно мы эту компоненту не наблюдаем, но мы фиксируем признаки, которые с ней коррелированы. Имея жизненный опыт, мы можем подсознательно по отдельным признакам формировать представление об интеллекте собеседника. Та процедура, которой при этом пользуется наш , и есть, по сути, факторный анализ. Наблюдая за тем, как те или иные явления проявляются совместно, , используя формальную процедуру, выделяет факторы, как отражение устойчивых статистических закономерностей, свойственных окружающему нас миру.
Выделение набора факторов
Мы показали, как фильтр Хебба выделяет первую главную компоненту. Оказывается, с помощью нейронных сетей можно с легкостью получить не только первую, но и все остальные компоненты. Это можно сделать, например, следующим способом. Предположим, что у нас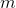 
входных признаков. Возьмем 
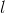линейных нейронов, где 
.
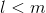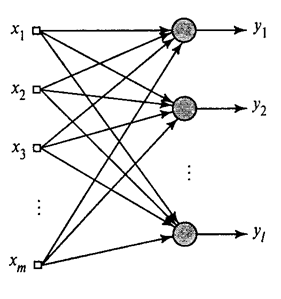
Обобщенный алгоритм Хебба (Хайкин, 2006)
Будем обучать первый нейрон как фильтр Хебба, чтобы он выделил первую главную компоненту. А вот каждый последующий нейрон будем обучать на сигнале, из которого исключим влияние всех предыдущих компонент.
Активность нейронов на шаге n определяется как
А поправка к синоптическим весам как
где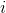 
от 1 до 
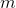, а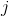 
от 1 до 
.
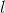Для всех нейронов это выглядит как обучение, аналогичное фильтру Хебба. С той лишь разницей, что каждый последующий нейрон видит не весь сигнал, а только то, что «не увидели» предыдущие нейроны. Этот принцип называется повторным оцениванием. Мы фактически по ограниченному набору компонент производим восстановление исходного сигнала и заставляем следующий нейрон видеть только остаток, разницу между исходным сигналом и восстановленным. Этот алгоритм называется обобщенным алгоритмом Хебба.
В обобщенном алгоритме Хебба не совсем хорошо то, что он носит слишком «вычислительный» характер. Нейроны должны быть упорядочены, и обсчет их деятельности должен осуществляться строго последовательно. Это не очень сочетается с принципами работы коры , где каждый нейрон хотя и взаимодействует с остальными, но работает автономно, и где нет ярко выраженного «центрального процессора», который бы определял общую последовательность событий. Из таких соображений несколько привлекательнее выглядят алгоритмы, называемые алгоритмами декорреляции.
Представим, что у нас есть два слоя нейронов Z1 и Z2. Активность нейронов первого слоя образует некую картину, которая проецируется по аксонам на следующий слой.
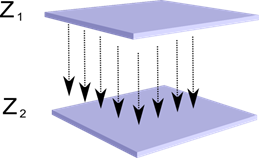
Проекция одного слоя на другой
Теперь представим, что каждый нейрон второго слоя имеет синаптические связи со всеми аксонами, приходящими с первого слоя, если они попадают в границы определенной окрестности этого нейрона (рисунок ниже). Аксоны, попадающие в такую область, образуют рецептивное поле нейрона. Рецептивное поле нейрона – это тот фрагмент общей активности, который доступен ему для наблюдения. Всего остального для этого нейрона просто не существует.
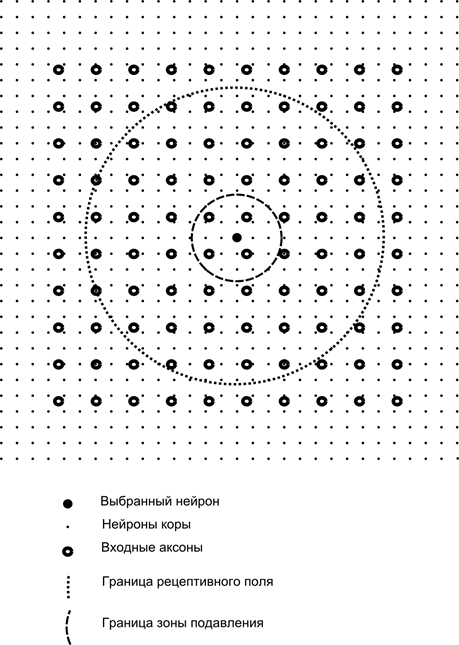
Помимо рецептивного поля нейрона введем область несколько меньшего размера, которую назовем зоной подавления. Соединим каждый нейрон со своими соседями, попадающими в эту зону. Такие связи называются боковыми или, следуя принятой в биологии терминологии, латеральными. Сделаем латеральные связи тормозящими, то есть понижающими активность нейронов. Логика их работы – активный нейрон тормозит активность всех тех нейронов, что попадают в его зону торможения.
Возбуждающие и тормозящие связи могут быть распределены строго со всеми аксонами или нейронами в границах соответствующих областей, а могут быть заданы случайно, например, с плотным заполнением некого центра и экспоненциальным убыванием плотности связей по мере удаления от него. Сплошное заполнение проще для моделирования, случайное распределение более анатомично с точки зрения организации связей в реальной коре.
Функцию активности нейрона можно записать:
где –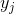 
итоговая активность, – 
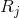множество аксонов, попадающих в рецептивную область выбранного нейрона, 
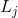– множество нейронов, в зону подавления которых попадает выбранный нейрон, 
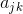– сила соответствующего латерального торможения, принимающая отрицательные значения.
Такая функция активности является рекурсивной, так как активность нейронов оказывается зависимой друг от друга. Это приводит к тому, что практический расчет производится итерационно.
Обучение синаптических весов делается аналогично фильтру Хебба:
Латеральные веса обучаются по анти-Хеббовскому правилу, увеличивая торможение между «похожими» нейронами:
Суть этой конструкции в том, что Хеббовское обучение должно привести к выделению на весах нейрона значений, соответствующих первому главному фактору, характерному для подаваемых данных. Но нейрон способен обучаться в сторону какого-либо фактора, только если он активен. Когда нейрон начинает выделять фактор и, соответственно, реагировать на него, он начинает блокировать активность нейронов, попадающих в его зону подавления. Если на активацию претендует несколько нейронов, то взаимная конкуренция приводит к тому, что побеждает сильнейший нейрон, угнетая при этом все остальные. Другим нейронам не остается ничего другого, кроме как обучаться в те моменты, когда рядом нет соседей с высокой активностью. Таким образом, происходит декорреляция, то есть каждый нейрон в пределах области, размер которой определяется размером зоны подавления, начинает выделять свой фактор, ортогональный всем остальным. Этот алгоритм называется алгоритмом адаптивного извлечения главных компонент (APEX) (Kung S., Diamantaras K.I., 1990).
Идея латерального торможения близка по духу хорошо известному по разным моделям принципу «победитель забирает все», который также позволяет осуществить декорреляцию той области, в которой ищется победитель. Этот принцип используется, например, в неокогнитроне Фукушимы, самоорганизующихся картах Коханена, также этот принцип применяется в обучении широко известной иерархической темпоральной памяти Джеффа Хокинса.
Определить победителя можно простым сравнением активности нейронов. Но такой перебор, легко реализуемый на компьютере, несколько не соответствует аналогиям с реальной корой. Но если задаться целью сделать все на уровне взаимодействия нейронов без привлечения внешних алгоритмов, то того же результата можно добиться, если кроме латерального торможения соседей нейрон будет иметь положительную обратную связь, довозбуждающую его. Такой прием для поиска победителя используется, например, в сетях адаптивного резонанса Гроссберга.
Если идеология нейронной сети это допускает, то использовать правило «победитель забирает все» очень удобно, так как искать максимум активности значительно проще, чем итерационно обсчитывать активности с учетом взаимного торможения.
Пора заканчивать эту часть. Получилось достаточно долго, но очень не хотелось дробить связанное по смыслу повествование. Не удивляйтесь КДПВ, эта картинка проассоциировалась для меня одновременно и с искусственным интеллектом и с главным фактором.
Алексей Редозубов (2014)
Автор: AlexeyR
