Моделирование пуассоновского процесса

Введение

Одним из важнейших процессов, наблюдаемых в природе, является пуассоновский точечный процесс. Поэтому важно понять, как такие процессы можно моделировать. Методы моделирования различаются в зависимости от типа пуассоновского точечного процесса, т. е. пространства, в котором протекает процесс и однородности или неоднородности процесса. Мы не будем заинтересованы развитием пуассоновского точечного потока или с важными приложениями его в различных областях. Чтобы этот материал показался интересным, читателю настоятельно рекомендуется прочитать соответствующие разделы в Феллере (1965) и Синларе (1975) для основной теории и некоторые разделы в Триведи (1982) для приложений в ИТ.

На первом шаге мы определим пуассоновский процесс на [0;+∞). Процесс полностью определяется семейством случайных событий, которые происходят в определённые случайные моменты времени 0 < T1 < T2 <… Эти события могут относиться ко множеству вещей, таких как ограбление банков, рождению пяти близнецов, и аварии с участием такси Монреаля. Если N(t1,t2) — это количество событий, происшедших за временной интервал (t1,t2), то часто выполнены два следующих условия:

• Для непересекающихся интервалов (t1,t2) и (t3,t4) случайные величины N(t1,t2) и N(t3,t4) независимы
• N(t1,t2) распределено также как и N(0,t2-t1), т. е. распределение числа событий за определённое время зависит только от длины этого интервала.

Удивительным фактом является то, что эти два условия влекут за собой, что все случайные величины N(t1,t2) распределены по закону Пуассона и что существует такая неотрицательная константа λ, что N(t,t+a) распределено по закону Po(λa) для любых неотрицательных t и a>0. См., например, Феллер (1965). Таким образом, пуассоновское распределение происходит вполне естественно.

Предыдущее понятие может быть обобщено на R^d. Пусть A — некоторое подмножество R^d, а N — случайная величина, принимающая только целые значения. Пусть X₁,...X_N — набор случайных векторов, принимающих значение в A. Тогда мы говорим, что X_i задают равномерный или однородный пуассоновский процесс на А, если

• Для любого конечного набора попарно неперескающихся подмножеств множества A А_i конечного объёма события N(A₁),...,N(A_k независимы
• Для любого борелевского подмножества B множества A распределение N(B) зависит только от объёма множества B

Примечание переводчика: Лучше было бы употребить слово «мера», но тем, кто не увлекается математикой, тогда пришлось бы объяснять с десяток страниц, а то и больше.

Опять же эти предположения влекут за собой, что все N(B) распределены по закону P(λVol(B)) для некоторого неотрицательного λ, котороый мы назовём интенсивностью, или параметром интенсивности однородного пуассоновского процесса на А. Примеры таких процессов в многомерном Евклидовом пространстве включают в себя бактерии на чашке Петри и места убийств в Хьюстоне.

Моделирование однородных пуассоновских процессов

Если нам необходимо смоделировать равномерный пуассоновский процесс на множестве A, принадлежащем R_d, то нам необходимо сгенерировать некоторое число случайных векторов X_i из A. По теореме 1.1 это можно сделать следующим образом:

Сгенерировать пуассоновскую случайную величину N с параметром λVol(A)
Сгенерировать независимые случайные вектора X1,..,XN, равномерно распределённые на А
RETURN Х1,...,ХN

Чтобы сгенерировать величину N, бесполезно использовать алгоритм со средней сложностью О(1), поскольку в конце алгоритма, мы потратим, как минимум Ω(n) операций. Поэтому, если используется этот алгоритм, настоятельно рекомендуется генерировать пуассоновскую случайную величину очень простым алгоритмом (со средним временем, растущим как О(λ) ). Для определённых множеств А, можно использовать другие методы, которые не требуют явной генерации пуассоновской случайной величины. Существует три случая, которые мы используем, чтобы это проиллюстрировать.

1. A=[0;+∞)
2. A — окружность
3. A — прямоугольник

Чтобы это сделать, нам понадобится интересная связь между Пуассоновским процессом и экспоненциальным распределением.

Теорема 1.2 предлагает следующий метод моделирования равномерного пуассоновского процесса на A=[0;+∞)

T = 0 (вспомогательная переменная для обновления "времени")
k = 0 (инициализировать счётчик событий)
REPEAT
Сгенерировать экспоненциальную случайную величину Е
k = k + 1
T = T + E/λ
T[k] = T
UNTIL Ложь (это бесконечный цикл; по желанию можно добавить критерий остановки)

Этот алгоритм просто реализовать, поскольку нет нужды генерировать пуассоновские случайные величины. Для других простых множеств A, существуют тривиальные обобщения теоремы 1.2. Например, когда A=[0,t]x[0,1], где t может равняться бесконечности, 0 < T1 < T2 <… — равномерный пуассоновский процесс с интенсивностью λ и U1,U2,… — последовательность независимых одинаково распределённых равномерно на [0,1] случайных величин, то (T1,U1),(T2,U2),… определяют пуассоновский процесс с интенсивностью λ на А.

Пример 1.1.

Равномерный пуассоновский процесс на единичной окружности
Если A — окружность с единичным радиусом, то разные свойства равномерного пуассоновского процесса можно использовать, чтобы получить несколько методов генерации (которые обобщаются на d-мерные сферы). Пусть λ — желаемая интенсивность.
Во-первых, мы просто могли бы сгенерировать случайную пуассоновскую величину N с параметром λπ, а затем вернуть последовательность N независимых одинаково распределённых равномерно на единично окружности векторов. Если мы применим метод порядковых статистик, предлагаемый теоремой 1.2, то пуассоновская случайная величина получается неявно. Например, перейдя в полярные координаты (R,φ) заметим, что для равномерного пуассоновского процесса R и φ независимы, и случайная величина R имеет плотность 2r, r меняется от 0 до 1, а φ равномерно распределена на [0;2π]. Таким образом, мы можем поступить следующим образом: Сгенерировать равномерный пуассоновский процесс 0 < φ1 < φ2 <… < φN с параметром интенсивности λ/(2π) на [0;2π] экспоненциальным методом и вернуть (φ1,R1),...,(φN,RN), где Ri — независимые одинаково распределённые случайные величины с плотностью 2r на [0;1], которые можно сгенерировать, взяв максимум из двух независимых равномерно распределённых на [0;1] случайных величин. Особой причины применять эспоненциальный метод к углам нет. Таким же образом мы могли подобрать и радиусы. К сожалению, порядковые радиусы не формируют одномерный равномерный пуассоновский процесс на [0;1]. Однако, тем не менее они образуют неоднородный пуассоновский процесс, и генерация таких процессов будет рассмотрена в следующем разделе.

Неоднородные пуассоновские процессы

Бывают такие ситуации, когда события происходят в «случайные моменты времени», но некоторые моменты более возможны, чем другие. Это случай прибытий в центры интенсивной терапии, предложений работ в компьютерных центрах и травмы игроков НХЛ. Для этих случаев очень хорошей моделью является модель неоднородного пуассоновского процесса, определённого здесь ради удобства на [0;+∞). Это самый важный случай, поскольку время чаще всего является «бегущей переменной».
Неоднородный пуассоновский процесс на [0;+∞) определяется неотрицательно определённой функцией интенсивности Λ(t), которую можно рассматривать как некоторого рода плотность с тем отличием, что её интеграл по [0;+∞) не обязательно равен 1(обычно, он расходится). Процесс определяется следующим свойством: для любой конечной коллекции непересекающихся интервалов A1,A2,...,Ak количество событий, происходящих в этих интервалах (N1,...,Nk) — независимые пуассоновские случайные величины с параметрами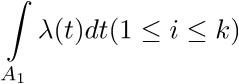

Теперь рассмотрим, как такие процессы можно смоделировать. При моделировании мы понимаем, что моменты времени, когда события происходят, 0 < T1 < T2 <… должны быть заданы в возрастающем порядке. Большая работа по моделированию неоднородных пуассоновских процессов была проделана Льюисом и Шедлером (1979). Весь этот раздел — переработанная версия их труда. Интересно наблюдать, что общие принципы генерации непрерывных случайных величин могут быть расширены: мы увидим, что существуют аналоги методом инверсии, отклонения и композиции.
Роль функции распределения займёт проинтегрированная функция интенсивности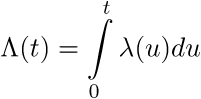

Мы начнём с того, что заметим, что если T_n = T, то T_n+1-T_n имеет функцию распределения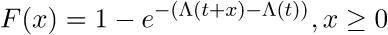

если функция Λ(t) неограниченно возрастает с ростом t. Это следует из того факта, что

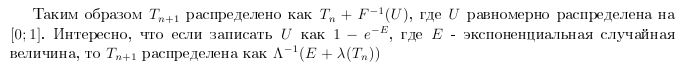
Иными словами, нам необходимо обратить Λ. Формально имеем (см. также Синлар (1975) или Бретли, Фокс и Шраге (1983)) алгоритм, основанный на обращении интеграла функции интенсивности (метод инверсии)

T = 0 (вспомогательная переменная)
k = 0 (счётчик)
REPEAT
Сгенерировать экспоненциальную случайную величину E
k = k+1
T = T + InvΛ(E+Λ(T)), (InvΛ - обратная функция к Λ)
T[k] = T
UNTIL False

Пример 1.2. Однородный пуассоновский процесс

Для особого случая λ(t)=λ, Λ(t)=λt несложно видеть, что InvΛ(E+Λ(T))=T+E/λ, в результате чего мы снова получаем экспоненциальный метод.

Пример 1.3.

Для моделирования утреннего потока автомобилей перед часом пик, мы иногда можем взять λ(t)=t, тогда Λ(t)=t^2/2 и получим шаг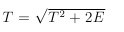

Если функцию интенсивности можно представить в виде суммы функций интенсивности, т. е. ,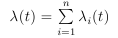

0 < T_i1 < T_i2 <… T_in — независимые реализации отдельных неоднородных пуассоновских процессов, то объединённая упорядоченная последовательность образует реализацию неоднородного пуассоновского процесса с функкцией интенсивности λ(t). Это относится к методу композиции, но разница теперь состоит в том, что нам нужны реализации всех компонентов процесса. Декомпозицию можно использовать, когда существует естественное разложение, продиктованное аналитической формой λ(t). Поскольку основная операция в слиянии процессов — взять минимальное значение из n процессов, для больших n преимущество может предоставить хранение моментов времени в куче из n элементов.

В итоге получим метод композиции:

Сгенерировать T[1,1],...,T[n,1] для n пуассоновских процессов и хранить эти значения вместе с индексами соответствующих процессов в таблице
T = 0 (текущее время)
k = 0
REPEAT
Найти минимальный элемент T[i,j] в таблице и удалить его
k = k + 1
T[k] = T[i,j]
Сгенерировать T[i,j+1] и вставить в таблицу
UNTIL False

Третий общий принцип — это принцип утоньшения (Льюис и Шедлер, 1979). Аналогично тому, что происходит в методе отклонения, предполагаем, что существует лёгкая доминирующая функция интенсивности λ(t) <= μ(t) для любого t.

Тогда идея состоит в том, чтобы сгенерировать однородный Пуассоновский процесс на части положительной полуплоскости между 0 и μ(t), затем рассмотреть однородный пуассоновский процесс под λ и, наконец, вернуть x-компоненты событий в этом процессе. Это требует следующей теоремы.

Теперь рассмотрим метод утоньшения Льюиса и Шедлера:

T = 0
k = 0
REPEAT
Сгенерировать Z, первое событие в неоднородном пуассоновском процессе с функцией интенсивности μ, который происходит после момента времени T. Присвоить T = Z
Сгенерировать равномерно распределённую на [0;1] случайную величину U
IF U <= λ(Z)/μ(Z)
THEN k = k + 1, X[k] = T
UNTIL False

Утверждается, что последовательность X_k так сгенерированная образует неоднородный пуассоновский процесс с функцией интенсивности λ. Заметим, что мы взяли неоднородный процесс 0 < Y1 < Y2 <… с функцией интенсивности μ и убрали некоторые точки. Насколько мы знаем, (Y_i,U_iμ(Y_i) — однородный пуассоновский процесс с единичной интенсивностью на кривой, если U_i независимые одинаково распределённые равномерно на [0;1] случайные величины в силу теоремы 1.3. Таким образом, подпоследовательность на кривой λ определяет однородный пуассоновский процесс с единичной интенсивностью на этой кривой (часть 3. теоремы 1.3). Наконец, взятие x-координат только этой подпоследовательности даёт нам неоднородный пуассоновский процесс с функцией интенсивности λ.
Неоднородный пуассоноский процесс с функцией интенсивности μ обычно моделируют методом инверсии.

Пример 1.4. Функция с циклической интенсивностью

Следующий пример также принадлежит Льюису и Шедлеру (1979). Рассмотрим функцию с циклической интенсивностью λ(t)= λ(1+cos(t)) с очевидным выбором доминирующей функции μ=2λ.

Тогда алгоритм моделирования примет вид:

T = 0
k = 0
REPEAT
Сгенерировать экспоненциальную случайную величину E c параметром 1
T = T + E/(2λ)
Сгенерировать равномерную на [0;1] случайную величину U
IF U <= (1+cos(T))/2
THEN k = k + 1, X[k] = T
UNTIL False

Нет нужды говорить о том, что можно использовать здесь теорему о двух милиционерах, чтобы избежать вычисления косинуса в большинстве случаев.

Заключительное слово об эффективности алгоритма, когда моделируется неоднородный пуассоновский процесс на множестве [0,t]. Среднее число событий, которое необходимо от доминирующего процесса, равно 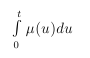в то время, как среднее число возвращённых случайных величин равно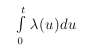
Отношение средних величин может быть рассмотрено как объективная мера эффективности, сравнимая в духе константы отклонения в стандартном методе отклонения. Заметим, что мы не можем использовать среднюю величину отношения, поскольку она, в общем случае, была бы равна бесконечности в силу положительной вероятности того, что ни одна величина не возвратится.

Автор: ProPupil

Источник