Как устроены Яндекс.Пробки? Откуда берутся исходные данные о дорожном движении? Как они превращаются в карту пробок? Всегда ли информация о пробках достоверна? Как это проверить? А главное, как сделать данные о пробках более точными? Для всего этого в Пробках используется статистика: наука одновременно сильная и коварная. В этой лекции аналитик Яндекс.Пробок Леонид Медников рассказывает студентам, как отличать достоверные результаты от случайных, и как статистика применяется в разных практических задачах.
Принцип работы Яндекс.Пробок достаточно прост. Чтобы описать его не требуется отдельная лекция. Приложения Яндекс.Карты и Яндекс.Навигатор при помощи GPS определяют местоположение устройства, на котором они запущены, и передают эти сведения на сервер. А он в свою очередь на основе этих данных создает картину пробок.
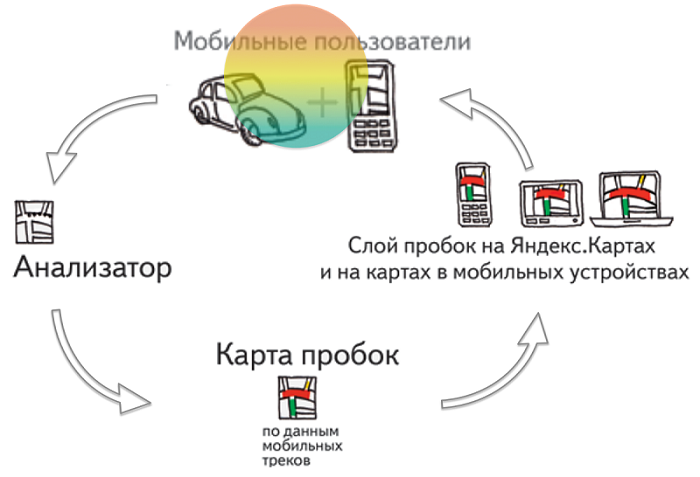
Но как именно это происходит? Вот это уже совсем нетривиальный процесс, требующий применения специальных алгоритмов и учета статистики. Как отличить медленно продвигающегося автомобилиста от пешехода или велосипедиста? Как убедиться в достоверности передаваемой информации? А главное, как сделать данные о пробках наиболее точными?
Самая первая проблема, с которой приходится сталкиваться при составлении карты пробок, заключается в том, что технология GPS далека от идеала и не всегда абсолютно точно определяет местоположение. Отслеживая передвижения одного объекта, можно получать довольно странные данные: мгновенные перемещения на достаточно большие расстояния, переход на обочину и т.д. В итоге мы можем получить следующую картину:
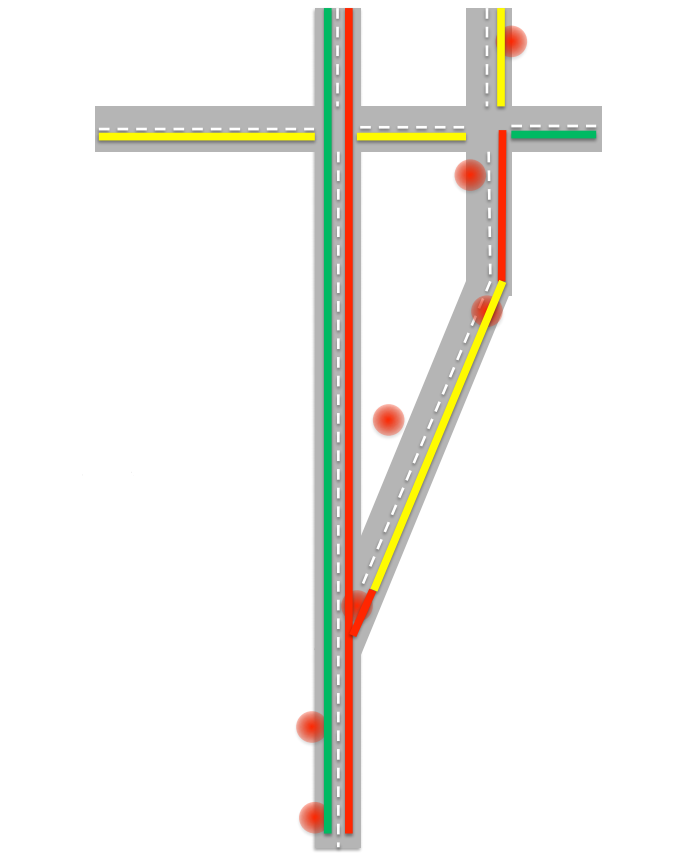
Алгоритму нужно принять решение, что это же это было. Для уточнения данных алгоритм попытается найти наиболее вероятный и разрешенный правилами маршрут. Далее нужно определить, какой перед нами объект? Ведь в пробке машины могут ехать со скоростью пешехода, а точность GPS не позволяет с уверенностью сказать, движется объект по проезжей части или по обочине. Тут можно учитывать несколько факторов: во-первых если количество объектов движущихся с небольшой скоростью достаточно велико, то мы можем предположить, что на этой дороге действительно есть пробка и автомобили едут медленно. Также мы можем учитывать историю скорости передвижения объекта за последние несколько часов. Допустим, если объект за последние четыре часа не развивал скорость больше 10-15 километров в час, то это, скорее всего, пешеход.
Итак, мы определили, скорость движения машин на определенном направлении за какой-то период, обработали их специальными алгоритмами, усреднили и в итоге получили примерную общую скорость движения потока. Все это происходит в режиме реального времени и на потоке, состоящем из сотен тысяч машин.
Алгоритмы
Как мы говорили выше, определением типа объекта, скорости его движения, усреднением скорости движения потока занимаются алгоритмы. Но как оценить качество их работы, понять, в какую сторону нужно двигаться, чтобы улучшить их?
Первая проблема решается запуском тестовых автомобилей в город. Как и обычные пользователи, они отсылают данные о своих передвижениях, но при этом мы точно знаем, какими были реальные условия. После этого можно на основе метрик сравнить реальную карту пробок на определенном участке с рассчитанной алгоритмами, и определить, насколько хорошо система справляется со своей задачей.
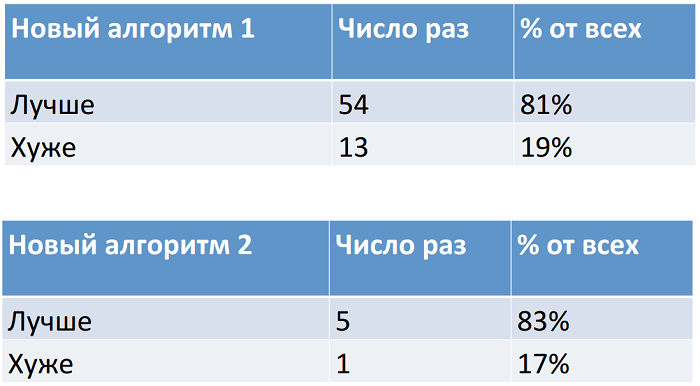
Сравнивая реальную ситуацию с результатами работы сразу нескольких алгоритмов, мы можем оценить, какой из них лучше. Допустим, что мы тестируем новый алгоритм и сравниваем его со старым. Прогоняем его на 67 отрезках и получаем следующие результаты:
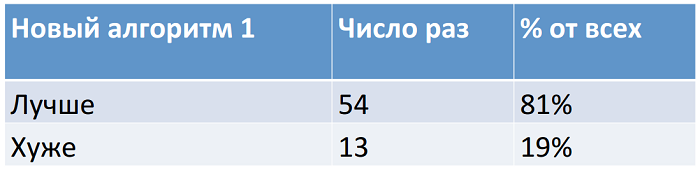
В 54 случаях новый алгоритм сработал лучше старого, а в 13 – хуже. По процентному соотношению верных ответов и ошибок новый алгоритм явно лучше. А теперь представим, что к сравнению мы добавляем еще один алгоритм. Но прогонялся он на меньшем количестве отрезков – на шести.
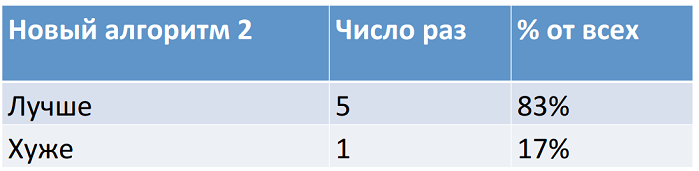
Процентное соотношение попаданий и ошибок у него еще лучше, чем у первого. Но стоит ли доверять проверке на таком малом количестве отрезков? Чтобы четко ответить на этот вопрос, обратимся к статистике.
Статистика
Для начала разберемся со случайными значениями. Допустим, мы подбрасываем монетку по три раза. Орел принимаем за ноль, а решку – за единицу. Всего у нас может получиться восемь комбинаций. Если мы посчитаем суммы выпавших значений для каждой из комбинаций, мы увидим, что крайние значения выпадают реже всего, а по мере приближения к центру вероятность увеличивается.
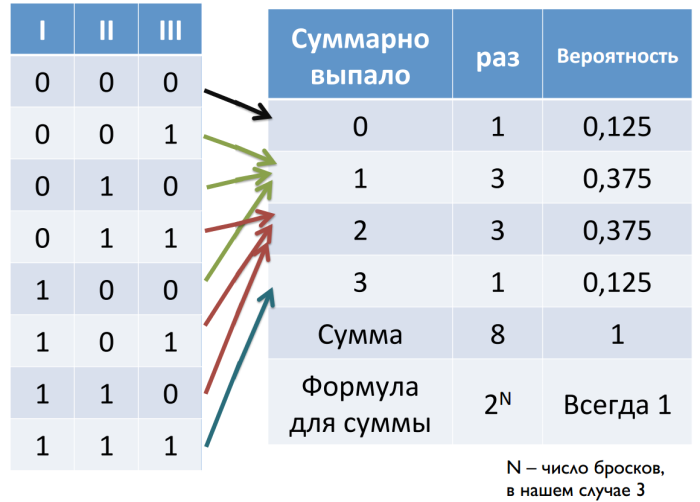
Теперь рассмотрим пример, в котором мы бросаем монетку N раз. Количество объектов мы примем за k, а количество комбинаций – за С.

Среднее и наблюдаемое среднее
Теперь поставим другую задачу. Представим, что у нас есть монетка, и мы хотим понять, ровная ли она, т.е. падает ли она на каждую из сторон с одинаковой вероятностью. Проверять эту гипотезу мы будем подбрасыванием монеты. Если монета ровная, то чем больше раз мы бросаем монету, тем ближе к среднему показателю должно быть наибольшее количество результатов. При этом, на низком количестве бросков вероятность сделать неверный вывод гораздо выше.
Почему мы вообще говорим о случайностях? Ведь ошибки в алгоритмах построения карты пробок чаще всего возникают по неким объективным причинам. Но не все эти причины нам известны. Если бы мы знали все причины, можно было бы составить идеальный алгоритм, и больше никогда его не улучшать. Но пока этого не произошло, мы вынуждены принимать некоторые ошибки алгоритмов за случайные величины. Поэтому мы проверяем, насколько лучше стал работать алгоритм при помощи примерно того же аппарата, что и гипотезу с ровной монетой. Только в данном случае в качестве базовой гипотезы мы принимаем то, что алгоритм вообще не изменился. А затем при помощи прогона данных через алгоритм определяем, есть ли перекосы в ту или иную сторону. И так же, как и в случае с монетой важно, чтобы таких прогонов было как можно больше, иначе у вероятность ошибиться будет слишком высока.
Если мы вернемся к нашему примеру с двумя алгоритмами, то мы по-прежнему можем с уверенностью сказать, что первый новый алгоритм лучше старого. А вот второй вызывает больше сомнений, несмотря на то, что процентное соотношение правильных ответов и ошибок у него лучше. Возможно, он действительно работает качественнее, но чтобы убедиться в этом, нужно провести больше проверок.
Автор: elcoyot






